物联网中MIBS轻量级密码的唯密文故障分析

李 玮 曹 珊 谷大武 李嘉耀 汪梦林 蔡天培 石秀金

1(东华大学计算机科学与技术学院 上海 201620) 2(上海交通大学计算机科学与工程系 上海 200240) 3(上海市可扩展计算与系统重点实验室(上海交通大学) 上海 200240) 4(上海市信息安全综合管理技术研究重点实验室(上海交通大学) 上海 200240)

物联网是物物相连的网络，它通过信息传感设备，按照某种协议把任何物品接入互联网，进行信息交换和通信，以实现对物品的智能化识别、定位、跟踪、监控和管理，广泛应用于智能家居、食品安全、智能电网、智慧医疗、智能交通、精准农业、智能环保、智慧物流、智能零售和公共安全等领域中[1-5].物联网的普及为人们的工作、学习和生活带来了极大的便利，但是，与传统的网络相比，它遭受到更大的安全风险.原因在于物联网中使用的终端设备存储和计算能力有限，不能有效地使用传统的密码算法实现信息的保密性、完整性和认证性.为了保护物联网中的数据免遭截获、篡改和伪造等威胁，国内外学者设计了具有一系列功耗低、吞吐量小、执行效率高和安全性能佳的轻量级密码，包括MIBS密码、LBlock密码、Simon密码和Simeck密码等[6-9].

2009年Lzadi等学者[6]于密码学和网络安全(CANS)会议上提出了MIBS轻量级分组密码，该密码具有典型的Feistel结构，分组长度为64 b，密钥长度分为64 b和80 b，具有功耗低、存储占用小等优点，适合在资源受限的RFID设备上使用.MIBS算法可以进行抵抗差分攻击、线性攻击、不可能差分攻击、积分攻击、中间相遇攻击和碰撞攻击等分析[10-15].

在物联网环境中，RFID等设备易受到故障分析(fault analysis, FA)的攻击.1996年Boneh等学者[16-18]针对RSA密码系统首次提出故障分析，以较低的攻击代价破译了密钥，引起了国内外研究学者的广泛关注.1997年Biham等学者[18]提出了差分故障分析(differential fault analysis, DFA)，并成功破译了DES密码.攻击者通过利用强磁场、电源电压毛刺、时钟毛刺、激光干扰、外界温度变化等方式对密码模块执行过程中的中间状态进行扰乱，从而获得错误的密文，并结合其他有效信息来破译主密钥.在物联网环境中，RFID等设备易受到这种攻击.

在故障攻击的实现中，基本假设至关重要，分为选择明文攻击(chosen plaintext attack， CPA)和唯密文攻击(ciphertext-only attack， COA).例如差分故障攻击、线性故障攻击、积分故障攻击、不可能差分故障攻击等的基本假设均为选择明文攻击，即攻击者可以选择获取任意明文的密文及相对应的错误密文.而仅有唯密文故障攻击的基本假设为唯密文攻击，即攻击者可以获得任意密文或错误密文.在唯密文攻击假设下，攻击者的能力最弱，一旦获得成功，将对密码系统的安全造成巨大威胁.因此，分析轻量级密码算法能否抵抗唯密文攻击假设下的故障攻击，对于物联网安全具有十分重要的意义.

目前，国内外还未有公开发表关于MIBS轻量级密码算法是否抵抗唯密文故障攻击方法的结果.本文深度剖析了MIBS密码的内部结构和运算，使用唯密文故障攻击对其进行了安全性分析，不仅实现了已有的“与”故障模型下的平方欧氏距离等7种区分器，而且提出了新型的双重“与”故障模型、新型Parzen-HW双重区分器和Parzen-HW-MLE三重区分器.结果表明，使用新型故障模型和区分器不仅提高了故障攻击效率，而且降低了故障攻击需要的故障注入数.该方法的提出，对于保护物联网等环境中的数据传输安全、增强密码系统的自主开发和分析能力，无疑都具有重要的现实意义和价值.

1 相关工作

自MIBS轻量级密码提出后，国内外研究学者相继使用差分攻击、线性攻击、不可能差分攻击、积分攻击、中间相遇攻击和碰撞攻击等传统密码分析方法对其安全性进行了分析.如表1所示，这些结果检测了MIBS密码缩减轮的安全性.

在故障攻击分析MIBS密码方面，研究学者通常使用选择明文假设下的差分故障攻击，完成破译MIBS密码全部轮.2011年王素贞等学者[19]在加密部分的最后2轮分别注入32 b故障，将密钥搜索空间降低到221.7.2018年王永娟等学者[20]基于S盒差分传播特性，在加密部分的最后一轮注入4 b故障，进而恢复最后一轮密钥的47 b，所需要的时间复杂度为217.2019年Gao等学者[21]通过计算S盒的差分分布的统计规律，在最后3轮中分别注入4 b故障，恢复主密钥的时间复杂度仅为22.本文分析了在唯密文攻击假设下，MIBS密码抵抗唯密文故障攻击的安全性.表2给出了针对MIBS算法的故障分析对比.

Table 1 Classical Cryptanalysis of MIBS表1 针对MIBS密码的传统密码分析

Table 2 Comparison of Fault Analysis of MIBS表2 针对MIBS算法的故障分析对比

2013年Fuhr等学者[22]首次针对AES密码提出了唯密文故障攻击方法，结合平方欧氏距离、汉明重量和极大似然估计等区分器，仅需要320,288和224个故障注入，可以恢复最后一轮密钥.2017年李玮等学者[23]将唯密文故障攻击应用在LED密码上，并新增了拟合优度区分器和拟合优度—平方欧氏距离双重区分器，用于降低所需的故障注入数.以上2种分析方法都是针对SPN结构的密码.2018年李玮等学者针对Feistel结构的LBlock轻量级密码，新增了双重区分器，提高了故障攻击的效率[24].从目前的研究可以看出，改进的唯密文故障攻击的方法均是通过优化选择单区分器和双重区分器来降低故障注入数.结合物联网环境和MIBS密码的设计特点，本文提出的唯密文故障攻击不仅增加了新型的双重区分器和三重区分器，而且构建了新型的双重“与”故障模型，进一步提高了故障导入效率，减少了故障注入数.表3总结了AES算法、LBlock算法和MIBS算法的唯密文故障攻击所需故障注入的结果对比.

Table 3Comparison of Fault Injections to Decrypting theLast Subkey of AES, LBlock and MIBS

表3 破译AES，LBlock和MIBS密码最后一轮子密钥所需故障数对比

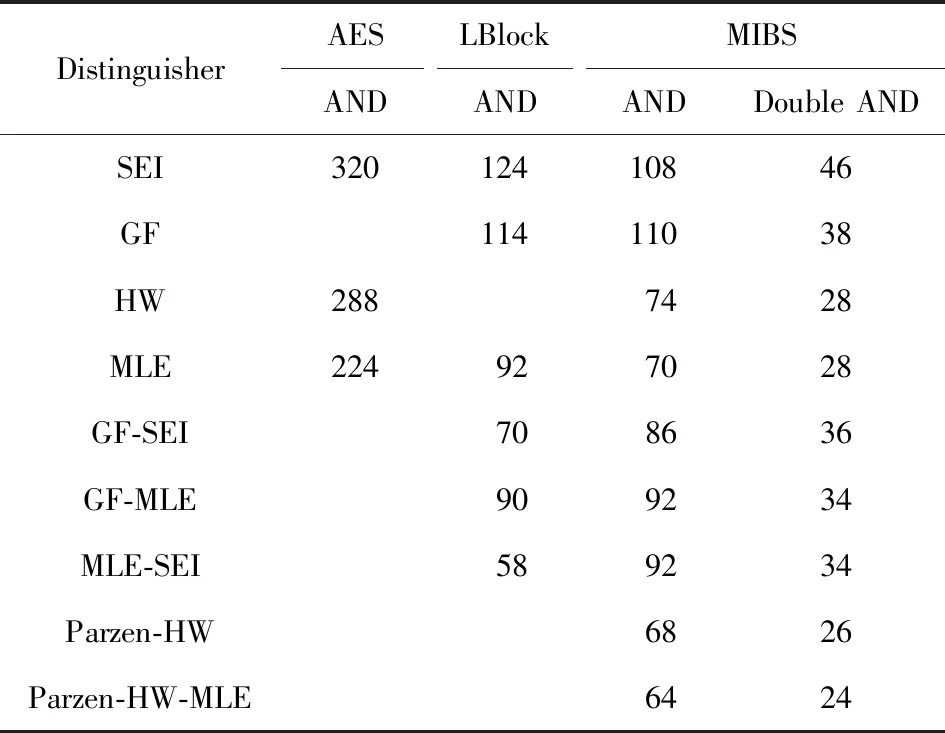
DistinguisherAESLBlockMIBSANDANDANDDouble ANDSEI32012410846GF11411038HW2887428MLE224927028GF-SEI708636GF-MLE909234MLE-SEI589234Parzen-HW6826Parzen-HW-MLE6424

2 MIBS算法介绍

2.1 符号说明

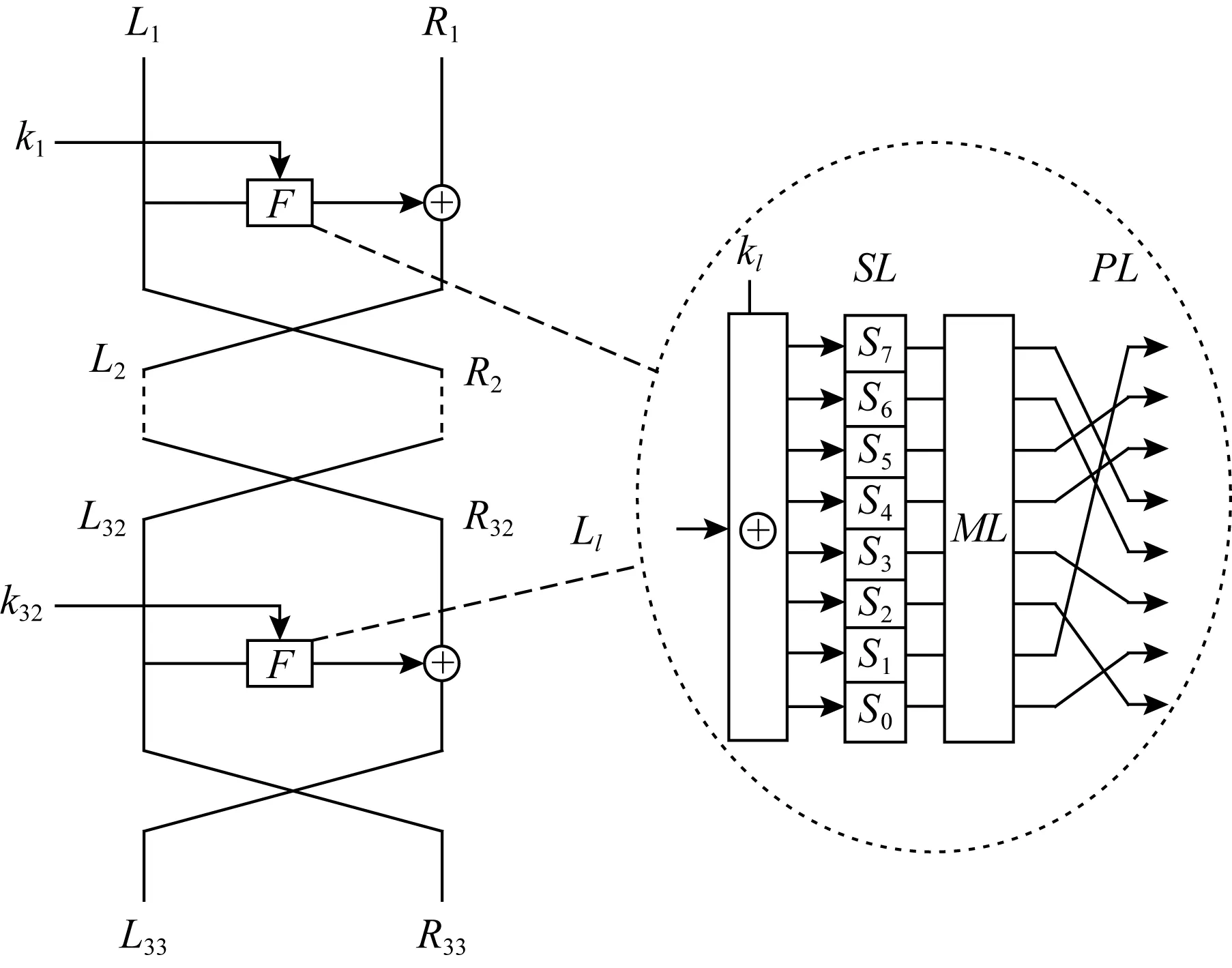
Fig. 1 The structure of MIBS图1 MIBS算法的结构

2.2 MIBS密码简介

MIBS密码的分组长度为64 b，MIBS-64版本和MIBS-80版本分别对应密钥长度为64 b,80 b，其迭代轮数均为32轮.算法由加密、解密和密钥编排3部分组成.解密与加密相同，所使用的子密钥顺序相反.结构如图1所示：

轮函数F由子密钥加、非线性层和线性层组成，表示为

Ll+1=F(Ll,kl)⊕Rl=
PL(ML(SL(Ll⊕kl)))⊕Rl，
Rl+1=Ll，

其中，SL为非线性层，ML和PL分别为线性层的混淆变换和置换.ML表达式为

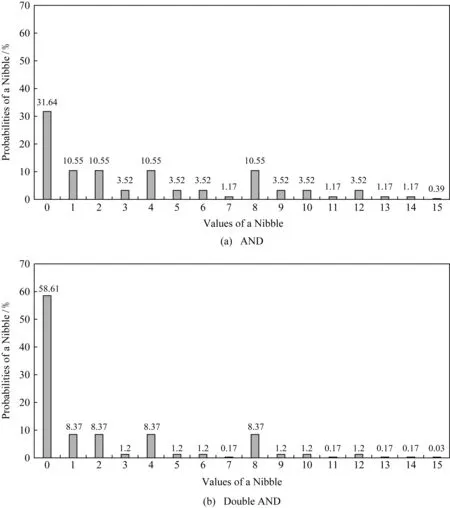
Fig. 2 The distribution of a nibble after fault injections图2 半字节被影响后的分布律

MIBS的加密部分如算法1所示.

算法1.MIBS密码的加密算法.

输入：明文X、密钥K；

输出：密文Y.

①L1‖R1=X;

② forl=1 to 32

③kl=Keyschedule(K);

④ end for

⑤ forl=1 to 32

⑥Ll+1=PL(ML(SL(Ll⊕kl)))⊕Rl;

⑦Rl+1=Ll;

⑧ end for

3 唯密文故障分析

3.1 基本假设和故障模型

本文使用的基本假设为唯密文攻击，即攻击者可以利用同一个密钥对多组随机明文进行加密，并在加密过程中导入任意故障，从而获得多组相对应的错误密文.

唯密文故障攻击中常使用的是“与”故障模型，在此基础上，本文构建了双重“与”故障模型，即

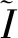
图2统计了上述故障模型的半字节分布，图2(b)双重“与”模型中的半字节分布比图2(a)“与”模型中的半字节分布差异更大.

3.2 攻击步骤

针对MIBS算法，本文验证了前人提出的SEI,HW,ML,GF,GF-SEI,GF-MLE和MLE-SEI等区分器,并提出了2种新型区分器Parzen-HW和Parzen-HW-MLE用于唯密文故障分析，均可以破译MIBS算法，具体有3个步骤.

Fig. 3 Faulty diffusion path in the last three rounds图3 最后3轮的故障扩散路径

素琴即无弦琴，该典与陶渊明相关，《晋书·隐逸传·陶潜》说陶潜：“性不解音，而畜素琴一张，弦徽不具，每朋酒之会，则抚而和之曰：‘但识琴中趣，何劳弦上声’”[4]。陆游认为弹琴能够悦性灵、养心、排闷，“举酒和神气，弹琴悦性灵”[3]831，“琴调养心安澹泊，炉香挽梦上青冥” [3]262，“援琴排遣闷，合药破除闲”[3]730。

通过中间状态、子密钥和错误密文之间的关系式可以求出k32的第1，2，4，5，6个半字节的值，由此可推出R32与k32的20位相关，依次可以求解k32的20个位.同步骤1，在第7个半字节导入故障，即可求得k32剩余12个位.

步骤3. 与步骤2类似，可以推出最后3轮所有子密钥，通过密钥编排方案即可恢复出主密钥.

3.3 区分器介绍

本文使用了9种区分器对MIBS密码进行分析，其中最后2种是本文所提出的新型区分器.

1) 平方欧氏距离区分器

2) 拟合优度区分器

拟合优度(goodness of fit， GF)区分器[23]是在已知样本分布率的情况下，通过计算一组样本与给定分布的拟合程度，从而找出正确的子密钥.图2给出了“与”、双重“与”故障模型下的理论分布.样本与已知分布率的拟合相似度越大，即误差越小，所对应的密钥候选值为正确子密钥的可能性越大，因此当GF取值最小时，所对应的密钥猜测值为正确子密钥：

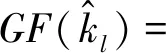
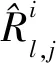
3) 汉明重量区分器

汉明重量(Hamming weight， HW)区分器[22]是计算中间状态和等长非零字符串的汉明距离，导入故障后会打破中间状态0,1的平衡，

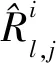
4) 极大似然估计区分器

极大似然估计(maximum likelihood estimate， MLE)区分器[22]是通过利用观察到的样本信息，反推最具有可能出现此样本结果的模型参数值.通过建立似然函数，计算每一组中间状态理论应该出现概率的乘积：

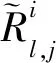
5) 拟合优度——平方欧氏距离区分器

拟合优度——平方欧氏距离(GF-SEI)区分器[23]先利用拟合优度算法过滤一部分明显不符合理论分布的样本所对应的密钥候选值，再利用平方欧氏距离进一步计算选择出最优的样本.该区分器的使用可以提高攻击效率，减少需要的故障注入数：

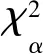
6) 拟合优度—极大似然估计区分器

拟合优度—极大似然估计(GF-MLE)区分器[24]先利用GF区分器挑选出与理论分布最接近的部分密钥候选值，再使用MLE区分器计算挑选出来的样本对应的概率，达到减少故障注入数和提高攻击效率的目的：

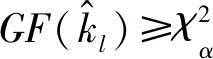
7) 极大似然估计—平方欧氏距离区分器

极大似然估计—平方欧氏距离(MLE-SEI)区分器[24]先利用MLE区分器筛选出密钥候选值，再计算出这些值对应样本的平方欧氏距离，从而达到减少故障注入数：

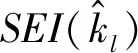
8) 窗估计—汉明重量区分器

窗估计—汉明重量(Parzen-HW)区分器是本文提出的一种新型双重复合区分器.Parzen窗估计是一种无参估计，由于Parzen区分器不需要假设数据分布，所以具有通用性的优点，但是要准确地估计窗函数需要大量的样本，因此使用Parzen区分器理论上需要更多的故障注入.通过结合HW区分器可以有效地避免上述问题，具体方法为先利用Parzen方法过滤大部分密钥候选值，然后再使用HW方法作精确筛选：

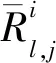
9) 窗估计—汉明重量—极大似然估计区分器

现有的区分器均为单区分器和双重区分器，本文提出的窗估计—汉明重量—极大似然估计(Parzen-HW-MLE)区分器是一种新型的三重区分器，有效地发挥了3种单区分器的优点，进一步提高了攻击效率，减少故障注入数.首先，攻击者构造窗函数，使用Parzen过滤大量密钥候选值

然后，结合汉明重量区分器进一步筛选：

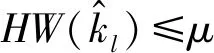
4 唯密文故障破译MIBS密码的实验分析

实验使用的PC配置为Intel Core I5-4200M，实验平台为Eclipse.使用Java编程语言软件模拟攻击环境.本文共进行了1 000次实验，均以超过 99%的成功概率破译MIBS-64版本和MIBS-80版本的密钥.附录A列出了实验所有数据.

图4(a)(b)表示在“与”、双重“与”故障模型下，所有区分器恢复子密钥的20 b所需要的成功概率和所需故障注入数的关系，其中横坐标表示故障注入数，纵坐标表示攻击成功率.不同颜色表示SEI,GF,HW,MLE,GF-SEI,GF-MLE,MLE-SEI,Parzen-HW和Parzen-HW-MLE等区分器的变化趋势.最终每一种区分器恢复子密钥的成功概率不小于99%.因而，在“与”、双重“与”故障模型下，攻击者恢复出最后一轮子密钥最少需要的故障注入为64个、24个，破译主密钥最少需要的故障注入为192个、72个.由表3可知，新型区分器Parzen-HW和Parzen-HW-MLE所需的故障注入数均较少.

图5(a)(b)表示在“与”、双重“与”故障模型下，使用所有区分器恢复子密钥20 b需要消耗的时间堆积图和故障注入数的关系.其中，横坐标表示故障注入数，纵坐标表示需要消耗的时间堆积，不同颜色线条分别代表各区分器.图6表示在相同区分器中，“与”、双重“与”故障模型下恢复出子密钥的平均时间对比图.其中，横坐标表示区分器，纵坐标表示时间，不同色块分别代表各故障模型.由图5和图6可知，SEI区分器和GF区分器所耗时间最多.和原有的“与”故障模型相比，双重“与”故障模型下各区分器需要的时间都大幅度减少.

Fig. 4 Comparison of success probability of recovering 20 b in two fault models图4 2种故障模型下恢复出20 b的成功率对比

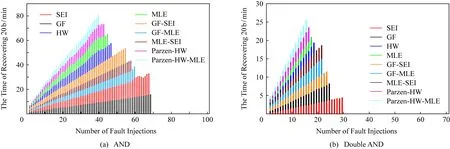
Fig. 5 Comparison of time of recovering 20 b using two fault models图5 2种不同故障模型下恢复20 b所需的时间对比

Fig. 6 Comparison of average time of recovering 20 b图6 恢复20 b所需的平均时间对比

在双重“与”故障模型中，所有区分器可以以较短时间和较少故障注入破译子密钥.并且，双重区分器Parzen-HW和三重区分器Parzen-HW-MLE在故障注入和时间消耗上均少于原有的区分器，因而，使用新型故障模型和新型区分器有效地提升了提高了故障攻击的效率，降低故障注入数和攻击时间.

5 结束语

本文提出并讨论了MIBS密码算法抵抗唯密文故障攻击的安全性.仿真结果表明：以MIBS密码为代表的Feistel结构密码算法易受到唯密文故障分析的威胁，在新型双重“与”故障模型下，新型Parzen-HW二重区分器和Parzen-HW-MLE三重区分器可以以较少的故障注入数、较低的时间花费破译MIBS密码，该方法的提出优化了唯密文故障攻击方法的效率和性能，为物联网中轻量级密码算法的安全性分析提供了参考.