调压室对水电站输水系统小波动过渡过程的影响

赵修龙 张健 李良权

摘要：为了减小水电站输水系统过渡过程中产生的水锤压力，常常会在输水系统中设置调压室。通过基于不考虑水体弹性的理论推导以及考虑水体弹性的数值模拟，对无调压室及有调压室两种方案下输水系统小波动的过渡过程进行比较分析，以便较为全面地对设置调压室或不设置调压室是否会对水电站输水系统小波动的过渡过程产生影响展开研究。研究结果表明：在相同布置条件下，无调压室及有调压室两种方案的输水系统的小波动过渡过程均是稳定的;设置有调压室的输水系统小波动的过渡过程要优于未设置调压室的输水系统小波动的过渡过程。从研究结果来看，设置调压室对水电站输水系统的小波动过渡过程具有改善作用。

关键词：输水系统; 调压室; 小波动; 过渡过程; 水电站

中图法分类号： TV732.5文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.02.036

1研究背景

在水电站有压管道输水系统中，过渡过程中产生的水锤现象是不容忽视的。机组负荷变化产生的水锤将会造成极大的危害，也是破坏管道输水系統的重要因素之一。因过渡过程中产生的水锤而引发的事故往往会造成压力管道的破裂、水力机械部件的损坏以及人员伤亡等[1-3]。设置调压室是减少水电站输水系统水锤压力常用的应对措施。调压室利用其扩大的断面和自由水面来反射水锤波，可以降低水锤的压力值，达到改善输水系统过渡过程的目的。

在水电站输水系统过渡过程计算中，当机组负荷发生微小变化，从而导致系统由一种恒定状态过渡到另一种恒定状态的过程叫做小波动。尽管小波动过渡过程并不如大波动过渡过程剧烈，但其对水电站调节品质的影响却不容忽略，这一点在水电站输水系统设计中具有重要的意义[4-6]。

目前，在调压室对水电站输水系统小波动过渡过程影响分析研究方面，俞晓东等学者采用了不考虑水体弹性的状态空间法和考虑水体弹性的非线性整体系统数值模拟法，对某设置有压室水电站的小波动过渡过程中的调压室波动情况和调节品质指标进行了比较分析，从而得出了两种计算模型的计算结果基本吻合的结论[7]。索丽生通过对设置上游和下游双调压室的水力-机械系统，导出了描述系统微小波动的线性微分方程组及其系数矩阵，从而对设置上、下游双调压室的水力-机械系统的小波动稳定性问题进行了研究[8]。何喻等人通过假定水流为刚性水体，推导出了长距离输水管道系统理想水轮机条件下的小波动微分方程组系数矩阵及其特征方程系数，从而对不设置调压室的长引水管道水电站的小波动稳定性问题展开了研究[9]。

本文通过采用不考虑水体弹性的理论进行推导的方法以及考虑了水体弹性的数值模拟的分析方法，对无调压室及有调压室两种方案下的输水系统小波动的过渡过程进行了比较，从而针对设置调压室对水电站输水系统小波动过渡过程的影响情况展开了分析研究。

2数学模型

2.1无调压室输水系统小波动稳定性

输水管道系统采用单机单管，无调压室，孤网运行;采用PI型调速器，不考虑水体弹性，根据刚性水体模型及小波动假设，忽略高阶微量，将方程进行线性化处理[10-12]。

无调压室的输水系统简图如图1所示。

机组的运动方程为

Tadφdt=p-pg=p-x-epφ（3）

PI型调速器的方程为

（bt+bp）Tddμdt+bpμ=-Tddφdt-φ（4）

式中，L1为上游引水隧洞的长度，m;A1为上游引水隧洞的截面积，m 2;Q为上游引水隧洞的流量，m 3/s;1为上游引水隧洞的水头损失系数;L2为压力管道长度，m;A2为压力管道的截面积，m 2;2为压力管道的水头损失系数;H1为上库水位，m;H2为水轮机蜗壳末端的水头，m;H3为尾水口的水头，m;H4为下库的水位，m;Ta为机组加速时间常数;pg为发电机吸收功率，kW;x为系统负荷，kW;ep为负荷自调节系数;p为发电机的输出功率，kW;φ为机组的转速变化率;bp，bt，Td分别为调速器的永态调差率、暂态转差系数和缓冲时间常数[13-15]。

假设水轮机为理想水轮机，即水轮机效率为常数，并且水轮机的力矩和流量的变化与水轮机导叶开度的变化成正比关系[16-18]。可知理想水轮机的出力和流量方程为：q=μ+12ξ，p=μ+32ξ。若忽略负荷自调节系数ep以及调速器的永态调差率bp的影响[19]，

令q=Q-Q0Q0，ξ=ΔHH0，Twi=LiQ0gAiH0（i=1～2），Tw=Tw1+Tw2，h0=1Q 20+2Q 20，Ta=[GD 2]n 20365P0，p=P-P0P0，Pg=Pg-P0P0，x=X-X0X0，φ=n-n0n0，μ=τ-τ0τ0

其中，下标“0”代表恒定状态的值。则（1）式和（2）式可整理为

dqdt=2Twμ-2H0+h0H0Twq（5）

（3）式和（4）式可分别整理为

dφdt=-2Taμ+3Taq-xTa（6）

dμdt=-1Tdbtφ+2Tabtμ-3Tabtq+xTabt（7）

上述管道系统状态变量只有3个，即φ，μ，q，由公式（5）～（7）可记为

DY=AY+Bx（8）

式中，D为微分算子，D=ddt;Y为系统状态变量;A为3×3阶系数矩阵。

A=0-2Ta3Ta

-1Tdbt2Tabt-3Tabt

02Tw-2H0+h0H0Tw

2.2含调压室输水系统小波动稳定性

输水管道系统采用单机单管，含调压室，孤网运行;采用PI型调速器，不考虑水体弹性，根据刚性水体模型及小波动假设，忽略高阶微量，将方程进行线性化处理[20]。

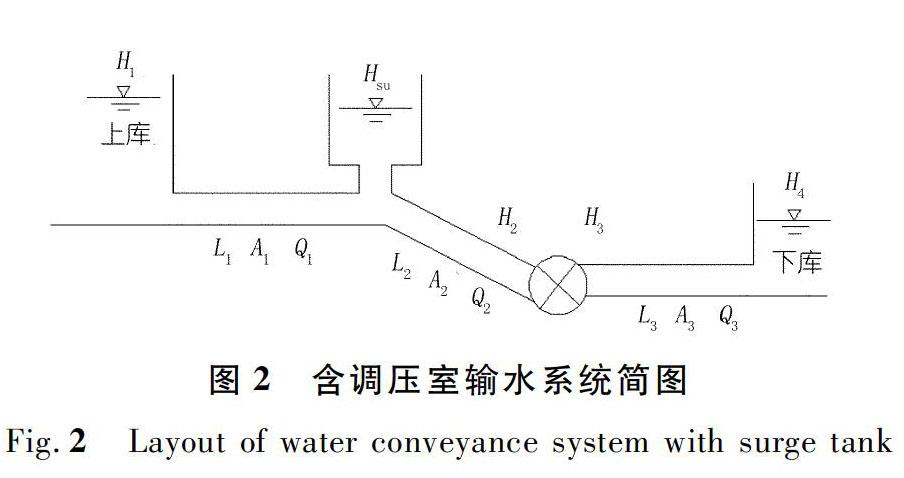
含调压室的输水系统简图如图2所示。

含调压室的输水系统的水流动力方程为

L1gA1dQ1dt=H1-Hsu-1Q 21（9）

L2gA2dQ2dt=Hsu-H2-2Q 22（10）

L3gA3dQ2dt=H3-H4-3Q 22（11）

流量连续方程为

Q1=FdHsudt+Q2（12）

式中，L1为上游引水隧洞的长度，m;A1为上游引水隧洞的截面积，m 2;Q1为上游引水隧洞的流量，m 3/s;1为上游引水隧洞的水头损失系数;L2为压力管道的长度，m;A2为压力管道的截面积，m 2;Q2为压力管道的流量，m 3/s;2为压力管道的水头损失系数;L3为尾水管道的长度，m;A3为尾水管道的截面积，m 2;3为尾水管道的水头损失系数;F为调压室的断面面积，m 2;Hsu为压力水头，m;H1为上库水位，m;H2为水轮机蜗壳末端的水头，m;H3为尾水口的水头，m;H4为下库水位，m [21]。

机组运动方程同公式（3），PI型调速器方程同公式（4）。

令T=FH0Q0，Twi=LiQ0gAiH0（i=1～3），k1=21Q 20H0，hi0=iQ 20（i=1～3），ξ=ΔHH0，q1=Q1-Q0Q0，q2=Q2-Q0Q0，z=Hsu-Hsu0H0，Tm=Tw2+Tw3，km=k2+k3。

其中，下标“0”代表恒定状态的值。公式（9）～（12）可化简为线性方程，即

dq1dt=-k1Tw1q1-1Tw1z（13）

dq2dt=-km+2Tmq2+1Tmz+2Tmμ（14）

dzdt=1Tq1-1Tq2（15）

机组运动方程及PI型调速器方程可分别整理成公式（6）和公式（7）。上述管道系统状态变量有5个，即φ、μ、q1、q2、z，由公式（6）、（7）、（13）、（14）、（15）可记为

DY=AY+Bx（16）

式中，D为微分算子，D=ddt;Y为系统状态变量;A为5×5阶系数矩阵。

A=0-2Ta03Ta0

-1Tdbt2Tabt0-3Tabt0

00-1Tw10-k1Tw1

02Tm0-km+2Tm1Tm

001T-1T0

在机组小波动稳定性分析中，需要给出调速器参数的整定范围，一般可考虑斯坦因建议值，即：bp+bt=1.5×TwTa;Td=3×Tw;Tn=0.5×Tw;取bp=0，因而bt=1.5×TwTa，其中Ta=GD 2N 2365P，Tw=LQgAH。

3算例分析

3.1基本资料

某水电站的主要参数如下：装机容量为252.6 MW，转动惯量60 000  t·m 额定流量为344.7 m 3/s，额定水头为81 m，额定转速为115.4 r/min，单根管线总长为886 m。

3.2小波动计算工况及结果分析

在进行输水系统小波动过渡过程稳定性理论分析时，采用了刚性水体模型，并假定负荷扰动，上游水位以及下游水位的扰动均是微小量。根据自动控制理论可知，电站输水系统小波动过渡过程的稳定性取决于系数矩阵的特征值λi的实部值的大小。若计λi=σi+ωi（σi、ωi分别为该特征值的实部和虚部），只有当系数矩阵的所有特征值的实部σi均为负值（即σi<0），系统才是稳定的，否则系统不稳定[8]，设置调压室和不设置调压室两种方案下的系数矩阵的所有特征值计算结果如表1所示。系数矩阵的全部特征值可以通过调用标准程序求得。通过对两种方案进行数值模拟，旨在对输水系统小波动过渡过程的影响进行分析。拟定的控制工况为：额定水头条件下的额定出力，给予5%的负荷扰动。图3为设置有调压室和不设置调压室两种方案下的机组蜗壳末端压力变化的过程线，图4为机组相对转速上升率变化过程线。

由表1可以看出：当两种方案的调速器参数、机组参数、输水系统布置均保持一致的情况下，无调压室方案及含调压室方案的水力-机械系统状态方程系数矩阵A的特征值实部σi（i=1～8）均为负值。这说明在两种方案下，该水电站输水系统的小波动过程是稳定的。

由图3～4可以看出：当两种方案的调速器参数、机组参数、输水系统布置均保持一致的情况下，无调压室方案的机组蜗壳末端的最大压力及机组最大转速的上升率均大于有调压室方案的相应值。这说明设置调压室对输水系统的小波动过渡过程更加有利。

4结 论

（1） 本文采用不考虑水体弹性，根据刚性水体模型及小波动假設，忽略高阶微量并将方程进行线性化处理的方法，推导出了无调压室及有调压室两种布置方案下的水电站输水系统小波动过渡过程系数矩阵的全部特征值，同时结合工程实例，对两种方案系数矩阵的特征值进行了比较研究。结果表明：无调压室方案及有调压室方案的水力-机械系统状态方程系数的矩阵特征值的实部均为负值，这说明在两种方案下，该水电站输水系统的小波动过程是稳定的。

（2） 通过考虑水体弹性的数值模拟并结合工程实例，对两种方案下的水电站输水系统小波动过渡过程中的机组蜗壳末端压力及相对转速的上升率进行了比较。结果表明：在无调压室方案下，输水系统小波动过渡过程中，机组蜗壳末端的最大压力及机组最大转速上升率均大于有调压室方案下的相应值。这说明有调压室的布置形式更加有利于改善水电站输水系统小波动的过渡过程。

本文研究结论对于实际水电站设计中是否需要设置调压室，以及设置调压室对输水系统小波动过渡过程的影响分析，将具有参考意义与借鉴作用。

參考文献：

[1]耿艳芬，王志力，金生.基于有限体积水锤方程的Godunov格式离散[J].计算力学学报，2007（4）：513-518.

[2]王洪亮，俞晓东，陈胜，等.吉林台二级水电站水力干扰过渡过程研究[J].水电能源科学，2009（5）：169-171.

[3]赵修龙，张健，俞晓东.基于有限体积法的有压管道水锤计算[J].水电能源科学，2014，32（2）：164-166，182.

[4]杨开林.电站与电泵中的水力瞬变及调节[M].北京：中国水利水电出版社.2000.

[5]俞晓东，张健，刘甲春.联合运行水电站水力机械系统小波动稳定性研究[J].水利学报，2017，48（2）：234-240.

[6]李路明，张健，陈胜.负荷扰动及工作水头对水电站小波动过渡过程的影响[J].水电能源科学，2016，34（2）：166-168，207.

[7]俞晓东，李高会，卢伟华.基于两种数学模型的水力—机械系统小波动稳定分析[J].水电能源科学，2009，27（5）：172-175.

[8]索丽生.设置上下游双调压室的水力-机械系统的小波动稳定分析[J].华东水利学院学报，1984（4）：33-43.

[9]何喻，张健，蔡朝.不含调压室的长引水管道水电站小波动稳定分析[J].中国农村水利水电，2012（12）：164-167.

[10]Wylie E B，Streeter V L.Hydraulic Transient[M].清华大学流体传动与控制教研室译.北京：水利电力出版社，1983.

[11]沈祖诒.水轮机调节[M].北京：中国水利水电出版社，1996.

[12]周建旭，郑源.水电站小波动稳定性分析方法的研究[J].江西水利科技，2004（3）：125-128.

[13]赵修龙，张健，何露.生态机组不同布置形式过渡过程研究[J].南水北调与水利科技，2014，12（5）：11-13.

[14]鲍慧琼.新疆某电站引水系统压力水道优化计算[J].水利建设与管理，2011，31（3）：20-24.

[15]焦洁，张健.中小型引水式水电站调压阀尺寸优化[J].水电能源科学，2012（5）：105-107，214.

[16]杨建东，詹佳佳，鲍海艳.调压室位置对调保参数的影响[J].水动力学研究与进展（A辑），2007（2）：162-167.

[17]杨建东，汪正春，詹佳佳.上游调压室设置条件的探讨[J].水力发电学报，2008（5）：114-117.

[18]鲍海艳，付亮，杨建东.基于调节保证的上游调压室最佳位置的确定[J].水利水电技术，2013（6）：117-120.

[19]刘启钊，胡明.水电站：第4版[M].北京：中国水利水电出版社，2010.

[20]蔡尚峰.自动控制理论[M].北京：机械工业出版社，1983.

[21]俞晓东，张健，苗帝，等.尾水岔管在调压室后交汇的水电站小波动稳定分析[J].水利学报，2014，45（4）：458-466.

（编辑：赵秋云）

引用本文：赵修龙，张健，李良权.调压室对水电站输水系统小波动过渡过程的影响[J].人民长江，2019，50（2）：202-206.

Impacts of surge chamber on small fluctuation transition process of water conveyance system in hydropower plant

ZHAO Xiulong ， ZHANG Jian 2， LI Liangquan

（1.POWERCHINA Huadong Engineering Corporation Limited， Hangzhou 311122， China;2.College of Water Conservancy and Hydropower Engineering， Hohai University， Nanjing 210098， China ）

Abstract： It is common to arrange a surge chamber in the water conveyance system of hydropower plants to reduce water-hammer pressure occurring during the transition process caused by small fluctuation. We compared and analyzed the small fluctuation in the transition process of water conveyance system with and without a surge chamber， in which water elasticity is considered and ignored respectively. The results show that under the same layout， both of the two schemes yield a rather stable transition process caused by small fluctuation; however， water conveyance system with a surge chamber performs better than that of the system without a surge chamber. The results reveal that setting up a surge chamber helps improve transition process of water conveyance system caused by small fluctuation.

Key words：water conveyance system; surge chamber; small fluctuation; transition process; hydropower plant