基于粗糙集—信息熵的水质综合评价方法研究

刘姗 张南 魏振

摘要：水质评价是水环境治理和水环境保护的基础，如何客观地设定各水质评价指标的权重是水质评价的重点和难点。首次将改进的基于粗糙集和条件信息熵权重的确定方法应用到水质评价中，科学、有效地确定了各水质评价指标的权重，并在此基础上进一步建立了基于粗糙集和条件信息熵的水质评价模型。利用该模型，对重庆市南川凤嘴江的实测水质数据进行了综合评价。应用结果表明：运用该方法得出的评价结果更加科学、合理，而且能够对同一等级的水质开展进一步的细化分级。研究成果可为水质监测和水质评价提供一种新的思路。

关键词：水质评价; 粗糙集; 信息熵; 指标权重; 评价方法; 水环境管理

中图法分类号：X143文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.02.014

1研究背景

水质综合评价是水环境管理与水环境保护的指导性工作，亦是水环境问题研究的重点。然而，水环境极其复杂且参数众多，因此，提取有效的评价指标，选择合理的方法，对于各评价指标进行权重的确定，是水质评价工作的核心与难点。目前，国内外对水质评价研究的方法有很多，主要有：多元统计分析法（因子分析、主成分分析、聚类分析等）[1-3]、人工神经网络法[4-6]、指数评价法（单因子评价法、内梅罗污染指数法）[7-9]、模糊综合评价法[10-12]等。各种评价方法各有其优缺点。

（1） 人工神经网络法是近些年来受关注度较高的水质评价方法，其评价结果客观且分辨率高。但是该方法对训练样本要求很高，而且实现过程复杂，使其实际应用受到了很大限制。

（2） 因子分析及主成分分析法能有效地筛选出水污染的主要影响因子，但是其要求的样本量是指标量的2～3倍，这样也就加大了计算的复杂程度[13]。

（3） 单因子评价法遵循的是一票否决的原则，其实现过程简单、实际操作性强，但用最差的单项水质指标来判定水质，难以科学、客观地反映水体功能[9]。

模糊综合评价方法融合了模糊数学理论，综合考虑了水环境系统的多项指标，缺点是各评价指标权重的确定需要依赖信息熵、层析分析等方法。采用信息熵方法赋权，只需计算一次就可以得到各指标的权重，从而避免了模糊评价方法中对多指标赋权时计算繁琐、工作量大等缺点[14]。

粗糙集理论不需要先验信息，而是直接对数据进行分析和挖掘，因此大大地减轻了主观性对水质评价结果的影响。同时，粗糙集理论具有较强的可扩展性，适宜于其他成熟算法的结合运用。熵是随机系统不确定性的定量表达工具。粗糙集理论将知识看作是关于论域的划分，从信息熵的角度出发，建立知识和信息之间的关系，对粗糙集理论应用进行扩展，可以解决粗糙集理论信息丢失和结果分类的问题。

本研究在阐述粗糙集和信息熵的基础上，提出了一种基于改进粗糙集与条件信息熵的权重确定方法，并进一步建立了新的水质综合评价模型;最后利用该模型，对重庆市南川凤嘴江的实测水质数据进行了综合评价。评价结果表明：将该方法用以对水质进行评价，得出的结果更加科学和合理。本文研究成果可为水质综合评价提供一种新的、更加科学的思路和方法。

2改进的粗糙集-信息熵权重确定方法

在粗糙集理论[15]中，知识被认为是一种分类的能力，通过引入代数学中的等价关系和集合运算来定义知识，并用信息系统来表示。该理论不需要先验信息，是处理不确定与不完整信息的有效工具。

（1） 定义1[16]。假设用S=（U，A，V，f）表示一个信息系统模型，其中，U={x1，x2，…，xn}为研究对象的非空有限集合，被称为研究论域;A=C∪D，C∩D=φ，C为条件属性集，反映对象的特征，D为决策属性集，反映对象的类别;V=∪a∈AVa为属性值的集合，Va为属性a的取值范围;信息函数f：U×A→V是一个映射，用于指定论域U中每个对象x的属性值，即對于x∈U，a∈A，则有f（x，a）=Va。若决策属性表不为空，则该信息系统被称为决策表。

熵是衡量一个系统无序性和混乱度的指标，它能够用确切的数值来描述知识[17]。粗糙集的代数表示直观性较差，难以理解，因此将粗糙集理论中的知识和信息熵建立起关系，从信息的角度去表达粗糙集的概念和运算[16]。

（2） 定义2[16]。在决策表S=（U，A，V，f）中，认为U上任意属性集合SA是定义在U上的子集组成的代数上的一个随机变量，其概率分布可通过如下方式来确定：

[S：p]=S1S2…Stp（S1）p（S2）…p（St）（1）

其中，p（Sj）=Sj/|U|;j=1，2，…，t。

（3） 定义3[16]。在决策表S=（U，A，V，f）中，决策属性集D（U/D={D1，D2，…，Dk}）对条件属性集C（U/C={C1，C2，…，Cm}）的条件信息熵I（D|C）定义为

I（D|C）=mi=1|Ci| 2|Ui| 2kj=1|Dj∩Ci||Ci|[1-|Dj∩Ci||Ci|]（2）

（4） 定义4[16]。在决策表S=（U，A，V，f）中，c∈C，则条件属性c的重要度定义为

NewSig（c）=I（D|（C-{c}））-I（D|C）（3）

条件属性c的权重W（c）定义为

W（c）=NewSig（a）a∈cNewSig（a）（4）

然而，上述的条件信息熵方法，可能会造成某些原为冗余属性的指标的重要度高于原为非冗余属性的指标。因此，在本研究中，将重要度不为0的非冗余属性列为高级优先级队列，而将重要度为0的冗余属性列为低级优先级队列，从而致使高级优先级队列中所有属性集的重要度均高于低级优先级队列中的属性集，这样就使得原为非冗余属性的指标权重高于原为冗余属性的指标权重，重要度较高的属性依然较为重要。同时，亦可以避免冗余属性权重为0的不合理权重的定义[18]。

（5） 定义5[18]。在决策表S=（U，A，V，f）中，c∈C，则条件属性c的优先度定义为

μ（c）=maxa∈{x|x∈C，Sig（x）=0}NewSig（a）Sig（c）>00Sig（c）=0（5）

（6） 定义6[18]。在决策表S=（U，A，V，f）中，c∈C，则条件属性c的权重NewW（c）定义为

NewW（c）=NewSig（C）+μ（c）a∈CNewSig（C）+μ（a）（6）

式中，NewSig（C）表示条件属性c的重要度;μ（c）代表条件属性c所处队列的优先级。

3水质综合评价模型

设水质系统为S=（U，A，V，f），其中，研究论域U={x1，x2，…，xn}为水质评价断面;A=C∪D，C∩D=φ，C为水质的指标集;D为各监测断面的分类集;V为水质属性值的集合;f∶U×A→V用于指定水质评价断面中各指标的属性值。通过上述改进的粗糙集-条件信息熵方法来构建水质综合评价方法，其步骤描述如下。

（1） 选取n个断面的m个水质指标构成断面的实测数据表，然后对数据进行标准化处理，以此去除数据的单位限制。采用系统聚类分析方法，对数据样本进行分类，根据定义1，将分类结果作为决策属性D。

（2） 根据地表水环境质量标准表（GB-3838-2002）[19]，对水质指标数据进行离散处理，结合步骤（1）所得的决策属性构成决策表。

（3） 依据条件属性和决策属性，分别对论域进行等价关系划分。根据公式（2）、（3）及公式（4），计算各个条件属性的重要度，以此来判断各条件属性的优先级别，并依据公式（5）～（6）来计算各条件属性的权重，从而得到权重矩阵。

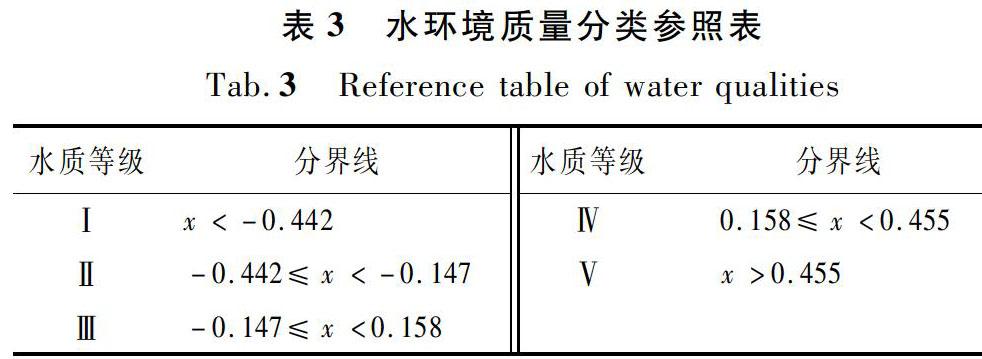
（4） 对地表水环境质量标准表（GB-3838-2002）进行标准化处理，得到水质评价标准表，并生成标准表矩阵;与权重矩阵相乘得到加权值，同一等级加权值的和即为该级水质综合标准的临界值，由此形成加权后的水环境质量分类参照表。

（5） 按照上述过程对水质量化表进行加权求和，从而得到各断面的综合得分;再根据水环境质量分类参照表进行水质等级的判定。

水质综合评价流程如图1所示。

图1水质综合评价流程Fig.1Comprehensive water quality assessment flow chart

4实例分析

本文采用文献[20]中给出的重庆市南川凤嘴江10个断面的实测水质数据作为研究对象，7项水质评价指标（c1-c7）分别为：溶解氧、五日生化需氧量、高锰酸钾指数、粪大肠菌群、挥发酚、氟化物以及铬（六价）。这7项指标在地表水环境质量标准表（GB-3838-2002）中的标准限值如表1所示。

依据地表水环境质量标准表（GB-3838-2002），对原始实测数据进行等级的划分，并以阿拉伯数字1～5代替水质指标集的值域{Ⅰ类，Ⅱ类，Ⅲ类，Ⅳ类，Ⅴ类}。对原始实测数据进行标准化处理及系统聚类分析。根据分析结果，可以将10个断面大致分为以下4类：

（1） 第2个断面单独为一类，决策属性记为1;

（2） 第9和第10个断面为一类，决策属性记为2;

（3） 第3，4，8个断面为一类，决策属性记为3;

（4） 第1，5，6和第7个断面为一类，决策属性记为4。

最终，形成水质监测数据决策表，详见表2。

利用前文中提到的粗糙集理论，对决策表进行等价关系的划分，并计算出各个水质指标的重要度。由此可对7个水质指标（c1-c7）进行等级分组，同时，利用改进的权重确定方法，计算各个水质指标的权重值（NewW），计算结果如下：

NewW（c1）=0.213，NewW（c2）=0.106，

NewW（c3）=0.043，NewW（c4）=0.184，

NewW（c5）=0.078，NewW（c6）=0.184，

NewW（c7）=0.191

參照前述文中提到的方法，获得水环境质量分类参照表，即各水质等级的分界线（详见表3）;计算各断面的综合得分，并与各等级分界线进行比较，由此得到各断面的水质等级（详见图2）。经过比较，评价结果与文献[20]中采用的BP模型评价法、Hopfield模型评价法、模糊综合指数法、灰色聚类法以及刘力[21]基于信息熵方法分析的评价结果基本一致。评价结果对比如表4所示。

由图2以及表4的结果可知，本文基于粗糙集-信息熵的水质综合评价方法，不仅能够给出客观、明确的水质评价结果，并且可以根据各个断面的综合得分，对同一水质等级下的各个断面的水质优劣情况进行比较分析。比如，本例的第4，9及第10个断面同为Ⅱ类水质，但是根据综合得分可知，第9个断面的水质要优于第10个断面的水质，也优于第4个断面的水质。对

于大型流域的水环境管理而言，在水质等级评定的基础上，细化各水质等级，可为水环境治理提供依据，对水环境管理和决策具有重要的参考价值。

5结 论

（1） 本文将粗糙集理论与信息熵相结合，形成了一个较完善的权重确定方法，给出了客观、明确的水质评价结果。

（2） 该方法稳定性高，较好地克服了传统水质综合评价中主观性强的缺点。

（3） 能够根据断面综合得分，对同一等级的评价对象进行细化考量，提高了水质评价的分辨率。

（4） 该方法概念清晰、评价出的结果科学合理，可进一步将其应用于水环境监测的相关工作中，具有深入研究的意义和推广应用的前景。

参考文献：

[1]Liu P， Hoth N， Drebenstedt C， et al. Hydro-geochemical paths of multi-layer groundwater system in coal mining regions - Using multivariate statistics and geochemical modeling approaches[J]. Science of the Total Environment， 2017（1）： 601-602.

[2]Fatoba J O， Sanuade O A， Hammed O S， et al. The use of multivariate statistical analysis in the assessment of groundwater hydrochemistry in some parts of southwestern Nigeria[J]. Arabian Journal of Geos-ciences， 2017， 10（15）：328.

[3]王刚， 李兆富， 万荣荣，等. 基于多元统计分析方法的西苕溪流域水质时空变化研究[J].农业环境科学学报， 2015， 34（9）：1797-1803.

[4]Najah A， El-Shafie A， Karim O A， et al. Application of artificial neural networks for water quality prediction[J].Neural Computing & Applications， 2013， 22（1）：187-201.

[5]曹建智， 张健. 人工神经网络在白洋淀水质评价中的应用[J]. 电子技术与软件工程， 2016（8）：261-262.

[6]刘丽颖， 官冬杰， 杨清伟，等. 基于人工神经网络的喀斯特地区水资源安全评价[J]. 水土保持通报， 2017， 37（2）：207-214.

[7]Kong Y， Pang Z， Wu C， et al. A comparative study of single factor and multivariate statistical methods for surface water quality assessment[J]. Water Policy， 2014（16）：157-167.

[8]Jie C， Qing L， Hui Q. Application of improved nemerow index method based on entropy weight for groundwater quality evaluation[J]. International Journal of Environmental Sciences， 2012， 2（3）：1284-1290.

[9]羅芳， 伍国荣， 王冲，等. 内梅罗污染指数法和单因子评价法在水质评价中的应用[J]. 环境与可持续发展， 2016， 41（5）：87-89.

[10]Li B， Yang G， Wan R， et al. Dynamic water quality evaluation based on fuzzy matter-element model and functional data analysis， a case study in Poyang Lake.[J]. Environmental Science & Pollution Research International， 2017（7）：1-11.

[11]Li R， Zou Z， Yan A. Water quality assessment in Qu River based on fuzzy water pollution index method[J]. Journal of Environmental Science， 2016， 50（12）：87-92.

[12]刘顿开， 吴以中. 改进的模糊综合评价法及在河道水质评价中的应用研究[J]. 环境科学与管理， 2017， 42（3）：190-194.

[13]安岩， 邹志红， 王晓静，等. 基于粗糙集理论的水质模糊综合评价[J]. 工业工程， 2015（1）：1-5.

[14]邹志红， 孙靖南， 任广平. 模糊评价因子的熵权法赋权及其在水质评价中的应用[J]. 环境科学学报， 2005， 25（4）：552-556.

[15]张文修. 粗糙集理论与方法[M].北京：科学出版社， 2001.

[16]鲍新中， 张建斌， 刘澄. 基于粗糙集条件信息熵的权重确定方法[J]. 中国管理科学， 2009， 17（3）：131-135.

[17]张继国，Singh P. 信息熵：理论与应用[M].北京：中国水利水电出版社， 2012.

[18]朱红灿， 陈能华. 粗糙集条件信息熵权重确定方法的改进[J]. 统计与决策， 2011（8）：154-156.

[19]国家环境保护总局，国家质量监督检疫总局.GB38382-2002地表水环境质量标准[S].北京：中国环境科学出版社，2002.

[20]郭劲松， 龙腾锐. 四种水质综合评价方法的比较[J]. 土木建筑与环境工程， 2000， 22（4）：6-12.

[21]刘力， 周建中， 杨俊杰，等. 基于信息熵的改进模糊综合评价方法[J]. 计算机工程， 2009， 35（18）：4-6.

引用本文：刘姗，张南，魏振.基于粗糙集—信息熵的水质综合评价方法研究[J].人民长江，2019，50（2）：75-78.

Research on water quality comprehensive evaluation method based on rough set and information entropy

LIU Shan，ZHANG Nan， WEI Zhen

（China Academy of Space System Science and Engineering， Beijing 100048， China）

Abstract： Water quality assessment is the basis of water environment management and protection. Objectively setting the weights of water quality evaluation indexes is the key and difficult point of water quality assessment. The improved weight determination method based on rough sets and conditional information entropy were applied to water quality assessment for the first time. The weight of each water quality evaluation index was determined scientifically and effectively. The water quality evaluation model based on rough set and conditional information entropy were further established. The application results show that the assessment results by this method are more scientific and reasonable， and can further give a fine classification of water quality at a same level. This method provides a new idea for water quality monitoring and evaluation.

Key words：rough set; information entropy; water quality assessment indicator weight; assessment method; water environment management