水沙数学模型技术在长江河口整治中的应用

徐学军 唐建华 王玉臻 赵升伟

摘要：为给河口整治提供参考和借鉴，基于DELFT3D模型系统建立了长江河口水沙数学模型，并利用实测水文、泥沙数据进行了率定、验证。大量实测资料验证结果表明，该模型的潮位、潮流和含沙量模拟平均精度分别可达91%，86%和72%，模型具有较好的模拟精度。该模型在长江河口治理规划研究、整治工程方案设计、施工设计、航道治理等方面应用效果良好，可为相关整治工程的决策和设计提供一定的技术支撑，值得进一步推广应用。

关键词：潮流数学模型; 泥沙数学模型; 整治工程; 长江河口

中图法分类号： TV148.1文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.02.008

长三角地区是目前中国经济发展速度最快、经济总量规模最大、最具发展潜力的区域，长江河口水土资源的开发利用对该区域经济社会的可持续发展举足轻重。目前，包括长江口河势控制、航道治理等在内的一系列整治工程正在如火如荼的进行中。水沙数学模型作为重要的技术手段，在长江河口大量整治工程的规划、设计、研究工作中发挥了重要作用，为相关整治工程的决策和设计提供了重要的技术支撑[1-4]。

笔者长期从事长江河口治理的相关工作，建立和完善了一套长江河口潮流、泥沙数学模型系统，该系统在长江河口治理规划研究、整治工程方案设计、施工设计、航道治理等方面发挥了一定的作用。本文对该水沙数学模型及其在长江河口整治中的应用进行了阐述，旨在进一步推广该模型技术，为类似的研究和河口整治提供参考和借鉴。

1长江河口水沙数学模型介绍

1.1水沙数学模型系统的选用

本研究所采用的水沙数学模型系统为荷兰代尔夫特水工研究所的DELFT3D。该模型是世界上最先进的模型系统之一，包含水动力、波浪、泥沙、水质、地形演变和生态等多个模块，各模块之间完全在线动态耦合，可用于河流、河口、海岸、湖库等水体的模拟[5]。

DELFT3D模型系统在国际上的应用十分广泛，应用范围包括荷兰、俄罗斯、德国、澳大利亚、美国、西班牙、英国、新加坡等。20世纪70年代中国香港地区开始使用，80年代开始在中国大陆有越来越多的应用，用于长江口、杭州湾、渤海湾、滇池等地区的研究[6-7]。

关于该模型的公式、求解方法等理论基础详见参考文献[5]，本文不再赘述。

1.2长江河口水沙数学模型的建立

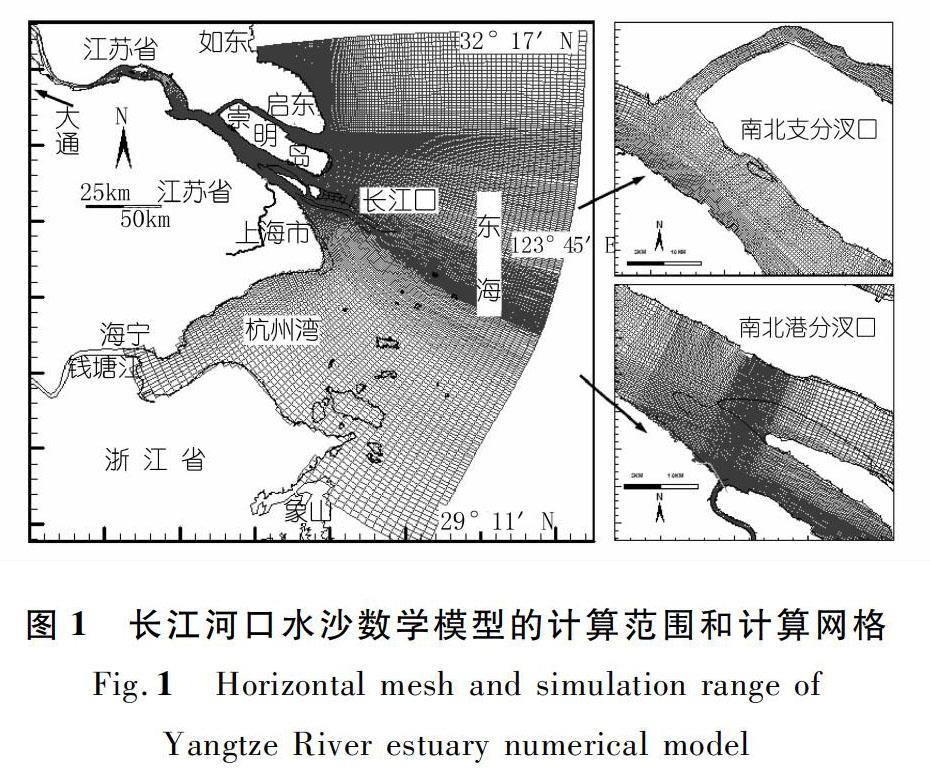
长江河口水沙（本文为潮流和泥沙）数学模型计算范围为整个长江口、杭州湾及近海水域，北至北纬32°17′吕泗，东至东经123°45′一线，南至北纬29°11′象山一带，西边界长江至大通、钱塘江至海宁。模拟范围东西向长约500 km，南北向宽约350 km（见图1）。采用DELFT3D模型系统自带的网格生成工具生成曲线正交网格，生成过程中兼顾网格的正交性、与岸线和河道走向的一致性以及与水下地形的协调性，并保持合适的分辨率，口内为100～500 m，局部加密至50 m左右，外海网格间距最大为7 km左右;网格总数为698×578（见图1）。

模型采用计算对应时段最新的水下地形。其中，外海采用对应时段的最新海图，河口水域结合近年测量资料综合取得，最终地形统一归化至85高程后插值至各網格点。

水动力模型北、东、南部开边界为外海潮位边界，采用经长期实测资料分析得到的11个分潮（4个日分潮：Q1、O1、P1、K1;4个半日分潮：M2、S2、K2、N2;3个浅水分潮：M4、MS4、M6）的调和常数预报的潮位。长江大通和钱塘江入海流量边界按实际的流量过程给定。对于泥沙模型，长江大通、钱塘江边界由实测含沙量过程控制;口外北、东、南部开边界结合历史实测资料采用概化的含沙量控制。

模型计算的初始水位、流速均取为0，初始含沙量由实测资料插值并结合卫星遥感图片解译取得。计算时间步长为30 s;糙率在深槽取值为0.010～0.016，浅滩取值为0.016～0.025;紊动黏滞系数为30 m 2/s;临界冲刷切应力为0.15～0.30 Pa，临界淤积切应力为0.05～0.10 Pa，冲刷常数为10-4～10-5 kg/（m 2·s），沉速为0.4～0.6 mm/s。

1.3水沙数学模型率定验证

为保证所建立的长江河口水沙数学模型的计算精度，采用长江口大量的实测水文、泥沙资料对模型进行了率定、验证。结果表明：无论是潮位、潮流、含沙量还是河床的冲淤，模型的计算值与实测值均吻合良好，模型模拟的重现度高。

为节省篇幅，本文仅给出部分水域潮位、潮流和含沙量的验证效果图，见图2～4。

1.4水沙数学模型模拟精度

为进一步说明水沙数学模型模拟的可靠性，本文按下式（1），根据模型计算值与实测值的对比，定量统计了潮位、潮流、含沙量的模拟精度。结果表明：长江河口水沙数学模型模拟潮位、潮流和含沙量的平均精度分别为91%，86%和72%（见表1）。

精度（%）=1-1样本数∑样本数i=1×|计算值i-实测值i|实测值i×100%（1）

2在河口整治中的应用

2.1在河口整治规划阶段的应用

长江河口南槽、南汇边滩为长江口与杭州湾的交汇地带，对该水域的整治既涉及到长江河口水土、航道资源的开发利用，也可能影响到长江口与杭州湾的水体交换，进而对杭州湾产生一定的影响。为此，利用建立的长江河口三维潮流数学模型，对长江口、杭州湾的水体交换规律进行了研究探讨，以期为长江河口南槽、南汇边滩的整治规划提供参考和依据。

杭州湾湾口水域水动力结构和代表断面余流的模拟计算及分析研究表明：长江口和杭州湾的水体交换主要在杭州湾北岸的近岸水域。由长江口向杭州湾扩散的水体主要在长江口与杭州湾交汇的汇角——芦潮港沿岸岸线以外4～5 km的-6～-8 m等高线以内范围，这股由长江口下泄、扩散的水团随涨潮流沿杭州湾北岸进入杭州湾，对长江口和杭州湾的物质交换具有重要作用。由北岸进入杭州湾的长江口水体在湾内涨、落潮流及钱塘江径流的综合作用下，最终在湾口中南部向外海输运、扩散（见图5）。此成果与陈吉余等[8]的研究结论基本一致。

2.2在河势控制工程设计中的应用

长江河口某河段拟在现状已完成的圈围工程基础上再实施促淤工程，以进一步缩窄该河段的河宽，达到保护岸滩、稳定整体河势的目的。为了给该工程的方案设计提供依据，利用建立的长江河口三维潮流、泥沙数学模型，对促淤工程的平面布置方案、促淤坝顶高程进行了多方案的比选和优化，最终推荐给出了如图6中虚线所示的促淤工程平面布置方案。该方案中，促淤工程总体上沿该水域的现状-3 m等高线布置，中部由一道“T”形促淤坝将促淤区分隔为两块，两促淤区均预留3 km宽口门;促淤坝顶高程均为0 m。

潮流数学模型计算结果表明，推荐的整治方案实施后，涨潮期在“T”形促淤坝东侧促淤区内流速降低明显，最大降幅达0.3 m/s;在“T”形促淤坝西侧促淤区内流速有所降低，最大降幅为0.2 m/s;促淤坝沿线水域流速也有所降低，最大降幅为0.2 m/s（见图6）。落潮期，在东侧促淤区内流速降低更为明显，最大降幅达0.5 m/s;在西侧促淤区内流速有所降低，最大降幅为0.3 m/s;促淤坝沿线水域流速也有所降低，最大降幅为0.4 m/s（见图6）。泥沙数学模型计算结果表明，推荐的整治方案促淤效果明显;整治方案实施后，东侧促淤区内最大淤积厚度约2.0 m;西侧促淤区由于现状滩面本身较高，促淤后上滩泥沙量有限，淤积厚度较小，该区域最大淤积厚度约1.0 m（见图7）。

2.3在河口整治工程施工中的应用

河口整治工程施工往往涉及到龙口合龙。龙口合龙是在前期预留的口门上修筑最后一段围堤，由于口门过窄，水流集中，流速增加，对施工非常不利，尤其是随着龙口的进一步缩窄，水流条件愈加恶劣，如龙口施工设计不合理而造成合龙失败，影响巨大，后果严重，必须慎重对待[9]。本研究以长江河口某整治工程龙口为例，利用建立的长江河口三维潮流数学模型，推求合龙过程中龙口水域的流速变化过程及规律，为龙口的施工设计提供依据。

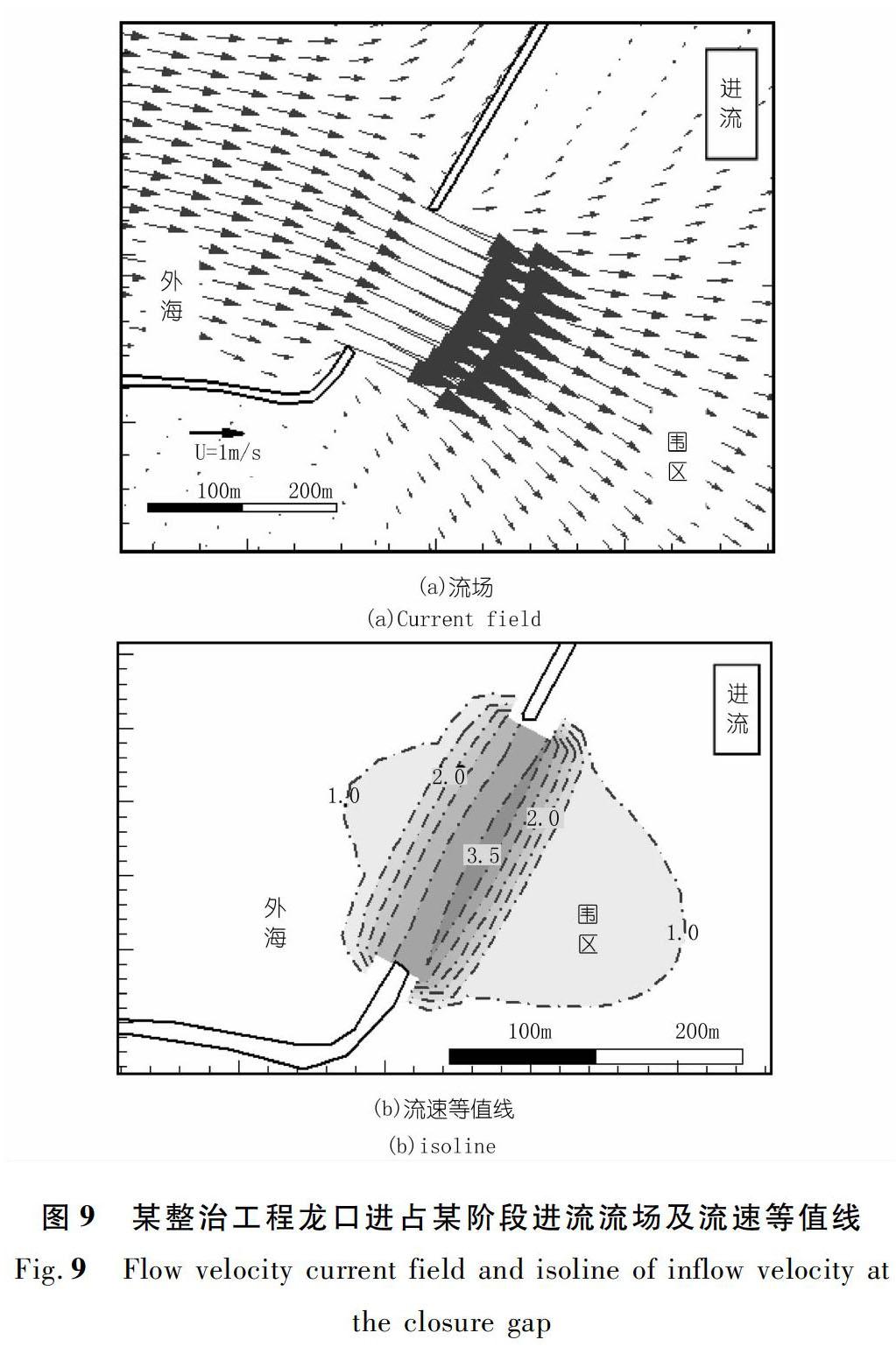
在龙口进占过程中，随着龙口宽度的减小和底坎高程的增加，龙口水域最大流速的变化如图8所示（龙口进流最大流速一般大于出流最大流速，限于篇幅仅给出进流的分析）。利用龙口水域最大流速等值线图（见图8），便可获知龙口进占过程中不同阶段的最大流速，合理安排龙口的压缩宽度、底坎的进占高程以及龙口的防护设计。

以龙口进占至宽200 m、底高程-1.0 m的阶段为例，说明龙口进占过程中龙口水域的水动力特征，见图9、图10。受龙口口门缩窄影响，龙口水域水流呈射流形态，若以1.0 m/s的流速作为分界，则龙口水域射流的宽度一般与龙口的口门宽度相适应，离口门越远，1.0 m/s的流速带的宽度越小。射流的长度一般为1～2倍的龙口口门宽度;受射流特殊的水动力影响，在龙口进占过程中不仅需在龙口沿线水域采取防冲护底措施，还需根据射流的范围在龙口上下游一定范围内的河床采取防冲措施。由于龙口堤头凸出，水流辐聚，三维结构明显，堤头水域流速最大，需采取必要的防护措施。

2.4在河口航道整治工程中的应用

长江河口某河段拟实施航道整治工程。通过整治将现状航道向南调整并疏浚，最小挖深0.7 m，最大挖深3.5 m，平均挖深2.0 m。为给航道的设计和维护提供参考，本研究利用建立的长江河口三维潮流、泥沙数学模型，模拟了航道整治后航道沿线的回淤过程及规律。结果表明：航道整治后，由于所在水域含沙量较高（平均为1.5～2.0 kg/m 3），航道沿线水域有不同程度的回淤，第一年平均回淤厚度约0.9 m，最大淤积在航道中上段的疏浚深度最大处，第一年回淤厚度达2.0 m（见图11）;考虑航道整治后回淤的影响，航道沿线的水深仍满足该段维护水深的要求。

为进一步验证泥沙数模计算所得的航道水域回淤厚度的可靠性，采用JTS145-2015《港口与航道水文规范》推荐的经验公式[10]估算了航道整治后沿线的回淤厚度，并与泥沙数模的结果进行比较，见图12。由图12可知：泥沙数模模拟与经验公式估算所得的航道沿线回淤厚度的分布总体上基本一致。两种方法得到的航道沿线回淤厚度的量值基本一致，故泥沙数模模拟的航道沿线水域的回淤厚度结果可靠。

为了解航道整治后的回淤过程，以航道中段水域为例给出了回淤厚度的时间变化过程，见图13。由于拟整治航道水域含沙量较大，航道整治工程实施后的0.5～1 a内航道回淤迅速，0.5 a和1 a内的回淤厚度分别占累计厚度的80%和90%以上。2 a内的回淤厚度占累计淤积厚度的96%以上。3 a后航道回淤基本达到平衡。

3结 语

本文基于DELFT3D模型系统，建立了长江河口水沙数学模型，大量实测资料的率定验证表明该模型具有较好的模拟精度，潮位、潮流和含沙量模拟的平均精度分别为91%，86%和72%。该水沙数学模型作为重要的技术手段，在长江河口大量整治工程的规划、设计、研究工作中发挥出了一定的作用，为相关整治工程的决策和设计提供了技术支撑，可进一步推广应用。

参考文献：

[1]张杰，卢金友，黄悦. 长江口平面二维水沙数学模型及初步应用[C]∥黄河水利科学研究院， 第六届全国泥沙基本理论研究学术讨论会论文集.郑州：黄河水利出版社， 2005： 1455-1464.

[2]徐照明，陈前海.徐六泾节点及白茆沙河段整治方案研究[J].人民长江， 2009， 40（13）： 3-5.

[3]劉怀汉，袁达全，裴金林，等.长江下游白茆沙水道航道整治对策[J].水运工程， 2010，（11）：86-92.

[4]孔令双，王巍，顾峰峰，等.长江口白茆沙河段航道整治方案初步研究[J].水道港口， 2010， 31（5）： 379-383.

[5]Deltares. Delft3D FLOW——Simulation of multi-dimensional hydrodynamic flows and transport phenomena， including sediments User Manual[Z].2011.

[6]趙庚润. 河口水库围堤龙口水流数值模拟[D].上海：上海交通大学，2009.

[7]陈青毅. 青草沙水库库内流动特征[D].上海：上海交通大学，2009.

[8]陈吉余， 陈沈良， 丁平兴，等. 长江口南汇咀近岸水域泥沙输移途径[J]. 长江流域资源与环境，2001，10（2）：166-172.

[9]唐建华， 刘玮祎， 李璐，等. 围海工程水动力学关键技术示范研究[M].武汉：湖北科学技术出版社，2014.

[10]JTS145-2015港口与航道水文规范[S].

引用本文：徐学军，唐建华，王玉臻，赵升伟.水沙数学模型技术在长江河口整治中的应用[J].人民长江，2019，50（2）：42-46.

Application of tidal flow and sediment numerical model in regulating Yangtze River estuary

XU Xuejun， TANG Jianhua， WANG Yuzhen， ZHAO Shengwei

（Shanghai Branch， Changjiang Survey， Planning， Design and Research Co.， Ltd.， Shanghai 200439， China）

Abstract： In order to provide reference and guidance for regulating river estuary， we built a tidal flow and sediment numerical model for Yangtze River estuary based on DELFT3D model system. Based on the measured hydrology and sediment data， the model was calibrated and verified. The verification results of a large number of measured data showed that the average accuracy of tidal level， tidal current and sediment concentration simulation can reach 91%，86% and 72% respectively. The model has good simulation accuracy and performs well in the application of Yangtze River estuary regulation planning， project design， construction design and regulation of river channels. This model provides technical support for the decision-making and the design of such regulation projects， which is worthy of further promotion.

Key words：tidal flow numerical model; sediment numerical model; Yangtze River estuary; regulation project