证券配对交易策略研究
卢海君


【摘要】本文基于协整方法对配对交易进行了研究,选取2015-2018年的上证50指数成分股前复权收盘价数据进行了实证分析,并将2018年作为样本外数据进行回测。实证结果表明:本文所构建的策略获得的超额收益为11.295%,且触发交易次数较多,盈利机会比较大,说明配对交易策略在中国市场是可行的。
【关键词】配对交易 选股 协整方法 阈值
一、引言
股票市场波动往往较大,投资者的资产收益会受到市场波动的影响而不稳定。配对交易作为一种市场中性策略应运而生,它是统计套利交易的一种形式,主要的思路是通过买卖具有长期相似趋势的股票对的短暂价差赚取收益。当这两个股票对的价差出现偏离时,通过做多股价被低估同时做空股价被高估的股票,并在价差逐渐收敛回复时做反向交易而获得套利收益。目前我国已推出融资融券业务,使得做空机制成为可能,这在一定程度上为配对交易提供了发展的空间。
其中,股票配对的选择是配对交易策略制定中的重要步骤,主要包括由Gatev等(2006)提出的基于距离的股票配对方法,由Vidyamurthy(2004)提出的基于协整的方法以及由Elliott等(2005)提出的基于随机价差的方法。中国学者在这方面也进行了相应的研究。王春峰等(2013)参考GGR模型,实证分析了中国市场2006-2009年的沪深300指数成分股,基于价格差异的最小距离法来配对股票,结果表明在市场环境变化的情况下仍然可以获得收益。王春丽和王佩帆(2017)则对配对交易策略进行了改进,利用相对价差进行实证分析,其交易绩效优于传统绝对价差的方法。欧阳红兵和李进(2015)则从配对交易的阈值选定角度出发,基于协整方法确定了最优的阈值,实现了利润最大化。
综上,本文将从投资者角度出发,研究基于协整法的配对交易策略。本文利用Wind数据库选取了上证50指数成分股,时间跨度为2015年1月1日至2018年12月31日,对其前复权日交易数据进行实证分析,选择合适的配对标的资产并选定合理阈值,构建出最优的套利策略。
(二)模型设定
本文将2015年1月1日至2017年12月31日的上证50指数成分股日收盘价作为形成期,剔除节假日,共有732天。其余时间则作为交易期。这50只股票,形成了1225个股票对。根据实际情况的不同,开仓平仓的阈值倍数k一般不等,本文假定k=0.5及k=1.1,止损线倍数则设定为2.5倍。
三、实证分析
(一)配对标的的选择
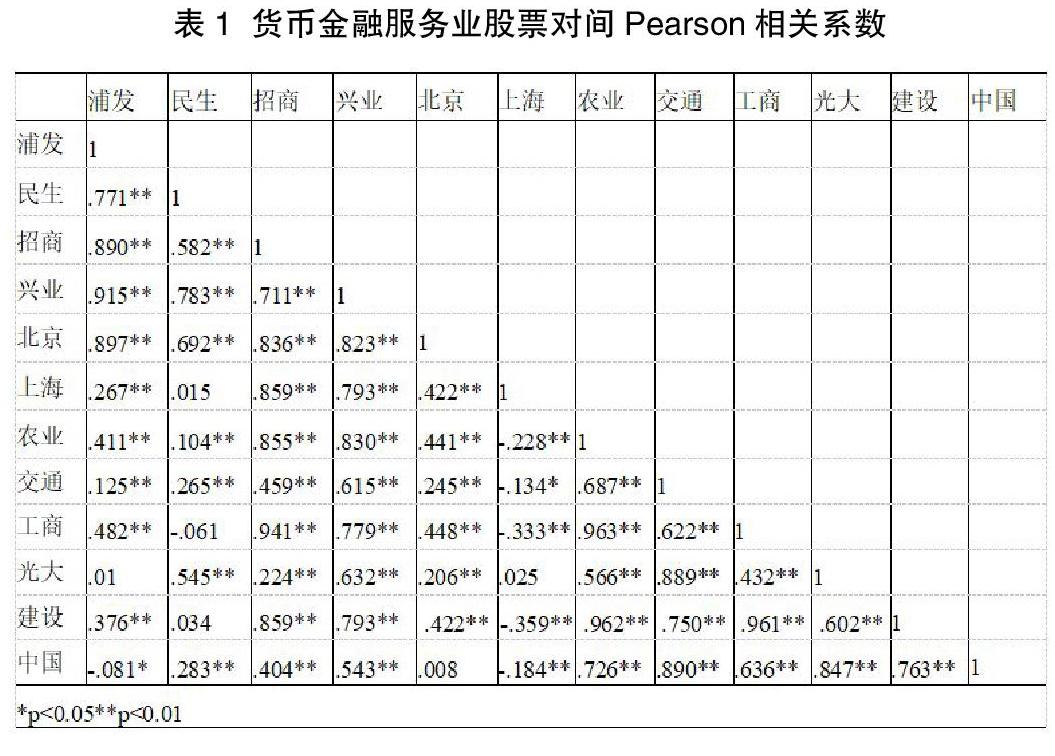
本文依据证监会行业的分类标准(2018年1季度)对上证50指数50只成分股进行行业归类。上证50指数成分股是最具代表性的50只股票,可以综合反映上海证券市场最具市场影响力的一批龙头企业的整体状况。另外,配对交易需要找到具有较强相关性的股票对,在同行业中筛选备择股票对,可以比较方便地解决这个问题。考虑到金融业和建筑业在上证50指数中占比相对较多,因此本文将以上证50指数成分股中的金融业(J)和建筑业(E)作为样本,其中,金融业包括货币金融服务业(J66)、资本市场服务业(J67)和保险业(J68)三个子行业的股票共17只,建筑业主要包含土木工程建筑业(E48),共4只。本文对样本内数据集(2015年1月1日至2017年12月31日,共有732个正常交易日)中的金融业和建筑业行业大类相关股票进行两两Pearson相关系数的计算。结果表明金融业中货币金融服务业的若干股票间相关系数最强,如表1所示。
其中工商银行与农业银行之间的Pearson相关系数达到了1%水平下的显著(0.963)。资本市场服务业和保险业大部分股票相关性并不是很大,而土木工程建筑业中的股票则显示出较高的相关性,其中中国建筑与中国中铁的Pearson相关系数达到了1%水平下的0.974,相关性最高,但由于后续拟合优度不够,因此本文将选择农业银行与工商银行这两只股票作为配对交易的股票对,其对数价格时序图呈相似的波动状态,且二者价格时序图的波动起伏大,若将这两只股票进行配对,那么它们进行配对的机会比较多。
(二)确定协整关系
股票對间要存在协整关系,前提是二者是同阶单整的,即其自身不平稳,但经过n阶后为平稳。通常来说,金融资产的对数价格可视为是一阶单整序列,本文将对农业银行和工商银行的日收盘价分别取对数后利用Python3.7进行ADF检验,以判断其是否满足协整关系。检验结果表明二者均不平稳。
接下来对其进行一阶差分后继续检验其单位根是否平稳。结果如表2。
这两只股票取对数后是非平稳的,但在经过一阶差分后都通过了检验,是平稳序列,因此为一阶单整序列,也就是可能存在着协整关系。利用OLS估计协整回归方程,得:log(GSYHt)=βlog(NYYHt)+εt。回归结果如下:
由表3可以看出,R2=0.929,说明拟合优度较好,二者之间存在着较强的相关关系。并且log(GSYHt)=-0.034+1.365×log(NYYHt)。则其残差Spreadt=log(GSYHt)+0.034-1.365×log(NYYHt)。据此可计算出均值μ=-0.018,标准差σ=0.03,并对其进行平稳性检验。结果显示P值为0.001,残差序列不存在单位根,也就是农业银行和工商银行之间存在着协整关系。
(三)确定交易阈值
接下来本文将利用Python3.7进行配对交易的样本外实测,以探讨该策略在中国市场是否可行。
由图2可知,配对交易信号一共触发了五次,分别出现在2018年4月至2018年5月之间、2018年6月至7月间、2018年9月至11月间、2018年11月至12月间以及12月末。
我们可以看到现金曲线变化波动比较大,12月末现金由最初的2000元升到了4229.7元,资产由原先的2000元升至2298.4元。说明该项配对交易策略盈利机会较多,且数额较大,可行性较强。
由表4知,在2018年的行情下,该配对交易策略的回测年化收益比基准收益(沪深300指数)要好一些。其中2018年12月27日的超额收益达到了11.295%。
四、结语
本文以上证50为例,按行业大类选取了货币金融服务业的两只高度相关股票,并采用协整方式对其进行了实证研究。研究表明,配对交易策略在2018年的样本外实测中,表现略好于基准指数的收益情况,并且在2018年的一年中,有相对多的触发交易信号,盈利机会较多。
参考文献:
[1] Gatev, E., Goetzmann, W.N. and Rouwenhorst, K.G. Pairs Trading: Performance of a Relative-Value Arbitrage Rule. Review of Financial Studies[J].2006,(19).
[2]Vidyamurthy, G. Pairs Trading, Quantitative Methods and Analysis[M]. John Wiley & Sons, Hoboken,2004.
[3]Elliott R. J., Van Der Hoek and Malcolm W. P., “Pairs Trading”, Quantitative Finance,2005,(3).
[4]王春峰,林碧波,朱琳. 基于股票价格差异的配对交易策略[J]. 北京理工大学学报(社会科学版),2013,(1).
[5]王春丽,王佩帆. 基于相对价差的股票配对交易策略优化[J]. 东北财经大学学报,2017,(4).
[6]欧阳红兵,李进. 基于协整技术配对交易策略的最优阈值研究[J]. 投资研究,2015,(11).
[7]丁涛. 配对交易策略在A股市场的应用与改进[J]. 市场研究,2013,(2).

