粉质黏土—非规则截面地铁车站结构地震变形特性

唐柏赞，陈 苏，李小军，庄海洋，吴旺成，苗 雨

(1.华东交通大学 土木建筑学院，江西 南昌 330013；2.中国地震局地球物理研究所，北京 100081；3.中国市政工程中南设计研究总院有限公司 深圳分院，广东 深圳 518034；4.华中科技大学 土木工程与力学学院，湖北 武汉 430074)

随着城市轨道交通的快速发展，建设场地条件越趋复杂，地铁车站结构形式也复杂多样，呈现不规则特征。地震灾害现象表明，粉质黏土地基震陷是引起地基失效造成地铁车站结构地震破坏的主要原因之一，是当前地下结构抗震分析领域的重要研究课题。因此，开展粉质黏土—非规则截面地铁车站结构动力学行为与地震损伤演变过程研究，具有重要的理论意义与工程应用价值。

近年来，国内外学者采用振动台试验及数值模拟对粉质黏土—地下结构地震反应特性开展了广泛深入的研究[1-7]。IWATATE等[8]通过振动台试验研究了箱型框架地铁结构的破坏过程，指出地铁车站结构的倒塌是由于结构中柱水平侧向刚度无法抵御地震动产生的剪切荷载作用；JAFARZADEH等[9]对埋地管线在均质和非均质场地中的地震反应进行了振动台试验研究。TANG等[10]开展了饱和软黏土地下结构在振动荷载作用下的动力反应和变形特性研究。MA等[11]采用振动台试验研究了软土层埋深对典型地铁车站结构地震反应特性的影响，并给出了地铁车站和隧道连接部位的损伤趋势。WANG等[12]基于等效惯性力方法进行了软土地基地铁车站结构的抗震计算。周灿朗等[13]采用反应位移法和时程分析法对地铁车站结构进行了抗震性能分析。杨林德等[14]通过软土地铁车站结构的振动台模型试验，得到了软土地铁结构动力反应规律。陈国兴等[2-3,15-16]以南京地铁车站结构建设背景，进行了一系列软土场地中地铁车站结构的大型振动台试验和数值模拟研究，系列试验与数值模拟相互验证并分析了不同结构形式地铁车站结构地震反应特性。赵伯明等[17]采用ANSYS-FLAC3D相结合的方法对2层3跨软土典型地铁车站结构进行强震响应的三维数值模拟。权登州等[18]针对黄土场地两层两跨地铁地下车站结构进行了振动台试验，研究了模型地基的竖向沉降和水平位移。然而，这些既有研究中，地铁车站的结构形式通常比较简单规整，未涉及非规则截面结构形式的地铁车站。

本文以粉质黏土场地中苏州星海广场站及上海南浦大桥站为对象，设计缩尺比例为1∶30上下层不等跨数(上层5跨下层3跨)地铁车站结构模型振动台试验。为满足振动台试验中多种类型物理量的有效测试，将阵列式位移计应用于模型试验中，实现土体变形测量；采用基于机器视觉研发的非接触性动态位移测试技术实现地铁车站结构损伤演变过程的可视化及数据化。根据实测数据归纳分析粉质黏土—非规则截面地铁车站结构体系的震陷、变形规律及失效机理，为地铁地下车站结构、地下商业街的科学设计、防震减灾提供支撑。

1 试验简介

1.1 土—地铁车站结构体系相似比设计

在南京工业大学振动台实验室进行缩尺模型试验。电液伺服地震模拟振动台主要技术指标：台面长×宽为4 860 mm×3 360 mm，最大载重量为15 t，水平最大振动加速度为±1.00g。采用叠层剪切型土箱填装地基土及地铁车站模型结构，土箱净尺寸为3 500 mm(振动方向)×2 000 mm(纵向)×1 700 mm(竖向)，该叠层剪切模型土箱能有效保证土体的剪切变形特性，较好地消除边界上地震波的反射或散射效应[19]。基于Buckingham-π定理，模型结构选取长度相似比Cl=1∶30、弹性模量相似比CE=1∶5、振动加速度相似比Ca=1∶2作为基础相似比，推导得其余量的相似比，分别为应力Cσ=1∶5，密度Cρ=1∶0.33，质量Cm=1∶9 000，时间Ct=1∶7.69，频率Cf=1∶0.13，速度Cv=1∶3.85。地基土选取剪切波速、密度、振动加速度为基本物理量，并在线弹性范围内分别推导出相似比关系。由于地铁车站模型缩尺较大，人工质量的设置难以实现，而基于忽略重力的模型，试验结果的适用性又大受限制，因此采用欠人工质量模型[20]。在模型结构每层楼板上均匀布置配重铅块以实现附加人工质量。

1.2 模型结构和地基土制作

本试验以苏州地铁1号线的星海广场站及上海地铁4号线南浦大桥站为原型结构，设计了缩尺比例为1∶30上下层不等跨数(上层为5跨，下层为3跨)的地铁车站结构模型，非规则截面上层5跨总宽为1 193.3 mm，下层3跨总宽666.7 mm，车站长1 333.3 mm，高467.4 mm，车站结构柱截面尺寸为20 mm×200 mm，柱间距为266.7 mm。按照原型与模型结构构件内力(弯矩、剪力)等效及施工可操作性原则，确定模型结构钢筋布置。车站模型采用微粒混凝土和镀锌钢丝制作，在试验前对微粒混凝土的材料物理特性进行了室内测定，其弹性模量平均值为7.8 GPa，立方体抗压强度平均值为4.4 MPa。模型地基土由1 350.0 mm厚的粉质黏土层与150.0 mm厚的黏土覆盖层构成，采用分层夯实法制备。模型结构制作过程如图1所示。

1.3 传感器布置

根据本次振动台试验目的，结合前期对地铁车站结构地震反应开展的振动台试验与数值模拟研究结果[21]，选取非规则截面中间跨为数据主观测面，规则截面中间跨为数据次观测面，非规则与规则截面转换交界面为辅助观测面，在观测面上布置传感器，如图2所示。图中：传感器编号D为激光位移计，共设5个；P为压阻土壤压力传感器，共设8个；PLT为动态位移标靶，共设11个；SAA为阵列式位移计，由8个可防止扭转变形的刚性段组成，段与段之间通过柔性接头相联结，7个普通刚性段集成MEMS振动加速度传感器及双轴重力振动加速度传感器，通过角度数据转换成变形数据；在模型结构侧墙顶部布设防水灯带，结构底板及中板处分别布置2台高清USB摄像头模组，共设4台，传感器编号为C，成对角分布，实现地震动作用下结构内部各构件失效过程的实时、无死角监测及视频资料采集；同时，在结构柱布设3～5个红色标靶圆(直径10 mm)。基于自主研发的非接触性动态位移测试方法，获得结构柱的侧向相对位移反应。

1.4 地震动选取及试验加载

试验选取Wolong地震记录(EW向)作为输入地震动，持续时间为180 s。Wolong地震记录是典型的1次震源2次破裂，2次破裂间隔时间较短，具有余震效应，能对结构造成累积损伤，加剧结构破坏，其振动加速度时程与傅里叶频谱如图3所示。试验采取阶梯加载的方式逐级加载，峰值振动加速度(aPGA)依次为0.10g，0.54g，1.24g，对应的Arias强度依次为0.086，3.265，14.761 m·s-1。每次峰值振动加速度调整时，输入0.05g白噪声进行扫频。

图2 粉质黏土地基中地铁地下车站结构模型传感器布置图(单位：mm)

图3 输入地震动的振动加速度时程和傅里叶频谱

2 粉质黏土—非规则截面地铁车站结构变形特性

2.1 粉质黏土—地铁车站结构体系震陷

2.1.1 地表震陷

本次振动台试验中，采用激光位移计及非接触性动态位移测试方法[22]测试粉质黏土地表震陷。强震动作用下地表震陷时程曲线(以下均为试验测得的模型数据)如图4所示。由图可知：地表震陷均大体经历了3个阶段，即震陷起步阶段—震陷强化阶段—震陷收尾阶段；地铁车站结构上方的地表震陷(测点D5)显著小于非地铁车站结构上方的地表震陷(测点PLT8)，这与地铁车站结构中空结构形式相关。

考虑到输入地震动的Arias强度反映了振动释放出的总地震能量，因此进一步研究地表震陷与Arias强度对应关系，如图4所示。由图可知：地表震陷3个阶段的转折点基本上分别与输入地震动总能量Arias强度为5%与95%的时刻相对应，有效强震持续时[23]地表震陷显著，表明地表震陷与Arias强度有较好的对应关系；图4(a)中地表开始震陷时刻稍提前输入地震动总能量Arias强度达到5%的时刻，这体现了地表震陷特性与地震动总能量间的时滞特性，地震引发的地表震陷起点时刻略提前地震动总能量的集中释放时刻。

图4 强震动作用下地表震陷时程曲线

图5给出了不同峰值振动加速度作用下地表测点震陷示意图。由图可知：0.10g地震动作用下，地表各测点震陷量较小，相差甚微；随着地震动峰值振动加速度的增大，地表震陷量逐渐增大，当峰值振动加速度不超过0.54g时，沿地基土纵轴线从地铁车站结构正上方至模型箱体边界，地表震陷量呈线性分布；1.24g地震动作用下，地表震陷量呈非线性分布。类似于已开展的地铁车站结构振动台试验及模拟的地表土震陷现象[18，24]，这是由于地基与地铁车站结构的竖向运动不协调引起的震陷反应差异。结果表明，强震作用下，地铁车站结构的存在改变了地表震陷的分布模式。

图5 地震动作用下地表震陷示意图(单位：mm)

为了研究地表震陷与水平位置之间关系，采用回归分析对地表震陷量与水平位置进行拟合，图6给出了不同峰值振动加速度作用下地表震陷量与水平位置拟合曲线。可以看出：地表震陷量与水平位置之间表现出明显的相关性；当峰值振动加速度不超过0.54g时，可采用形如式(1)的一次多项式表示；随着峰值振动加速度进一步增大，可采用形如式(2)的玻尔兹曼分布式表示；不同强度的地震动作用下，两者拟合参数及相关系数分别见表1。因此，基于力分布的地铁车站结构抗震设计时应充分考虑地震动强度对地表震陷的影响。

图6 地表震陷量拟合曲线

δ=Ax+B

(1)

(2)

式中：δ为收尾阶段的地表震陷量，mm；x为地表上位置点与模型箱体边界的水平距离，m；A，B，x0与dx为拟合参数。

表1 地表震陷拟合曲线参数

表2列出了不同峰值振动加速度作用下地铁车站结构上方的地表震陷量。由表2可知：结构侧墙上方的地表震陷量(如测点D2，D4)始终大于结构正中心上方的地表震陷量(如测点D3，D5)；对于同一截面，结构上方的地表震陷差值Δ可用侧墙上方测点与正中心上方测点的地表震陷差表示，即Δ2-3为测点D2与测点D3的差值；Δ4-5为测点D4与测点D5的差值，可见，随着峰值振动加速度的增大，地表震陷差值逐渐增大；与截面转换交界面(测点D4，D5所在横截面)相比，非规则截面地铁车站结构上方的地表震陷量较大于截面转换交界面的地表震陷量，尤其在结构侧墙位置处(如测点D2)。这是由于端头效应的影响[25]，地铁车站纵向端头处的地震动力反应较剧烈；非规则截面一侧的结构重量较大于规则截面一侧的结构重量，结构重心偏向于非规则截面一侧，强震作用下模型地基土逐步软化，土结动力相互作用中地铁车站结构逐渐向非规则截面一侧倾斜与扭转，从而非规则截面端头处上方的地表震陷较为显著，因此，非规则截面地铁车站结构上方的地表震陷具有显著的空间效应。

表2 地震动作用下地表震陷量

2.1.2 地铁车站结构沉降

为了解粉质黏土—非规则截面地铁车站结构体系竖向接触特性，在地铁车站结构顶板布置出露地表标靶(测点PLT10和PLT11)，采用非接触性动态位移测试方法，测试得到车站结构的竖向沉降。地震动作用下车站结构竖向沉降时程曲线及沉降过程如图7所示。由图可以看出：车站结构沉降受顶部土体的地震反应和瞬态位移控制，车站结构竖向运动与地表震陷发展规律较为一致；车站结构侧墙测点PLT10的竖向沉降始终小于结构正中心测点PLT11的竖向沉降；车站结构沉降差可用测点PLT10与测点PLT11的竖向沉降差表示，可知，在不同峰值振动加速度作用下，车站结构的沉降差均为负值，而同一位置地表上方的震陷差为正值(见表3)。这些现象说明：在强震作用下，车站结构出现不均匀沉降时，结构上方土体对车站结构约束作用减弱，因此车站结构与上方土体运动的同步性减弱，从而在楼板正中心位置呈现出土结分离现象。

图7 地震动作用下地铁车站结构沉降时程曲线及沉降过程

2.1.3 地铁车站结构相对上升高度与动土压力增量差关系

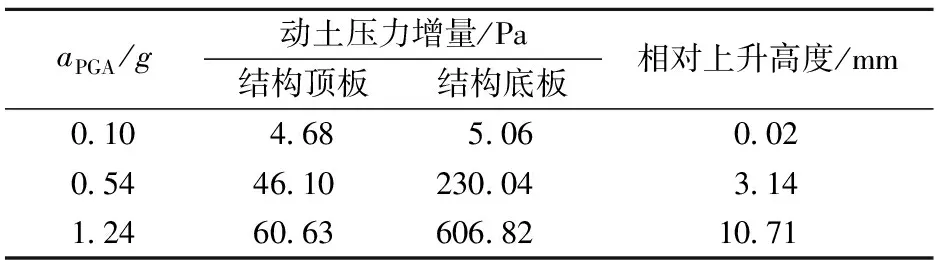
地铁车站结构相对土体上升高度可用地表测点PLT11与结构测点PLT8的竖向沉降差表示，其值见表3。可以看出，随着输入峰值振动加速度增大，车站结构相对上升高度逐渐增大。为研究车站结构上升运动机理，表3列出了车站结构顶板与底板的动土压力增量，对比分析发现，车站结构顶板动土压力增量明显小于底板动土压力增量，且底板与顶板两者间的动土压力增量差随着输入峰值振动加速度增大逐级增大，其与结构相对上升高度的变化规律基本一致。地铁车站结构相对上升高度与动土压力增量差的关系如图8所示，可见，随着输入峰值振动加速度的增大，结构底板与顶板之间的动土压力增量差逐渐增大，车站结构相对上升高度相应增加。因此，车站结构底板与顶板间的动土压力增量差提供了车站结构上升运动的推力。

表3 地铁车站结构顶板、底板动土压力增量与相对上升高度

aPGA/g动土压力增量/Pa结构顶板结构底板相对上升高度/mm0.104.685.060.020.5446.10230.043.141.2460.63606.8210.71

图8 地铁车站结构相对上升高度与动土压力增量差的关系

2.2 粉质黏土地基水平变形

在输入地震动作用下，地基土各测点在正负2个方向的水平位移如图9所示。由图可知：地基土水平位移幅值随输入峰值振动加速度的增大而逐渐增大，且随土层深度的减小而加速增加；由于输入地震动加速度具有方向性，在正负2个方向的位移不对等，从而地基土正向水平位移均大于负向水平位移的绝对值。

图9 地基土水平位移反应

图10(a)给出了采用SAA测试的水平相对位移反应。由图可见：随着土层深度的减小，地基土的水平相对位移逐渐增大；曲线斜率表现出先减小后增大的趋势，并在土层中部偏下(-1.05 m左右)出现明显的反弯点，最终呈现出浅部土层斜率最大，深部土层最小。该结果表明，强震作用下，粉质黏土地基中下部层间剪切位移最大，上部最小。

为了研究水平相对位移与土层深度之间关系，对水平相对位移幅值与土层深度采用非线性回归分析法进行拟合，图10(b)给出了其拟合曲线。可以看出，两者之间表现出明显的相关性，可采用形如式(3)的3次多项式表示，其拟合参数及相关系数见图10(b)。因此，对粉质黏土场地中非规则截面地铁车站结构采用反应位移法进行抗震设计时，水平相对位移沿土层深度的分布规律可考虑使用多项式表述。

y=ah3+bh2+ch+d

(3)

式中：y为水平相对位移幅值，mm；h为土层水平深度，m；a，b，c与d为拟合参数。

图10 地基土水平相对位移反应

2.3 地铁车站结构侧向变形与结构损伤

地铁车站结构侧向变形及可由此产生的层间剪切与车站结构损伤过程及特性关系密切，本实验在车站结构楼板布置高清摄像头，沿车站结构柱高度均匀布设位移测点，实现模拟地震条件车站结构损伤过程的实时采集及数据化。图11给出了1.24g地震动作用下车站结构柱的侧向相对位移。由图可知：车站结构的侧向相对位移与结构高度成正相关关系，在结构顶板处取得极大值；车站结构在地震动作用下正负2个方向的侧向相对位移形态大体相似，侧向相对位移分布并不对称，这种现象与地基土的水平位移反应规律一致，表明车站结构的侧向相对位移反应受到地基土的约束。同时发现，中板处最大层间位移为1.59 mm，顶板处最大层间位移为0.28 mm，相应各楼层最大层间位移角分别为1/163和1/535。该结果表明，车站结构上层侧向刚度较大，能有效限制结构侧向位移。根据城市轨道交通结构抗震设计规范(GB50909—2014)及地铁车站结构抗震性能水准研究[26]，钢筋混凝土矩形断面地下车站结构可修水平的层间位移角限值为1/250，表明非规则截面地铁车站结构在强震作用下出现损伤，且损伤主要集中在地铁车站结构下层构件上。

图11 1.24g地震动作用下地铁车站结构柱的侧向位移

图12给出了地铁车站结构非规则截面与规则截面的侧向相对位移。由图可知：非规则截面的侧向位移大于规则截面的侧向位移。根据震害经验、试验研究结果及各国规范的规定，判断是否满足建筑功能要求及衡量结构变形能力的合理可靠指标是层间位移角。因此，对比非规则截面地铁车站结构的层面位移角，规则截面地铁车站结构上层层间位移角较大，为1/340，下层层间位移角较小，为1/201。由于地铁车站结构可修水平的层间位移角限值为1/250，该结果表明，在强地震动作用下，地铁车站结构的下层均出现了损伤，尤其在非规则截面下层构件上，因此，浅埋地铁车站结构的下层构件是结构抗震薄弱环节，在地铁车站结构抗震设计中应考虑截面形式的差异性。

为研究地铁车站结构水平运动机理，表4列出了地铁车站结构非规则截面与规则截面的侧墙动土压力计算结果。可以看出，地铁车站结构侧墙动土压力随着输入峰值振动加速度增大而逐渐增大。对比地铁车站结构侧墙顶底部间的动土压力增量差与截面层间位移角发现，两者具有相似的变化规律，即在1.24g地震动作用下，地铁车站结构下层非规则截面动土压力增量差较大于规则截面动土压力增量差，地铁车站结构上层非规则截面动土压力增量差明显小于规则截面动土压力增量差。该结果表明，在强震作用下，粉质黏土与地铁车站结构接触面相互作用强烈，地铁车站结构变形受到周围土体的约束与作用，即地铁车站结构损伤主要受制于周围土体水平变形的影响。

图12 在1.24g地震动作用下地铁车站结构柱侧向相对位移反应

表4 地铁车站结构不同观测断面的动土压力增量及动土压力增量差

注：ΔP2-4，ΔP3-4，ΔP6-8，ΔP7-8分别为侧墙测点P2与P4，P3与P4，P6与P8，P7与P8的动土压力增量差。

3 震害分析

试验过程中：在0.54g地震动作用下，地铁车站结构下层柱振动明显，侧墙顶部灯带振动幅度较大；地表位于辅助观测面侧墙位置开始出现横向裂缝，随后在地铁车站结构端头位置出现沿振动方向的纵向裂缝；在1.24g地震动作用下，地表裂缝快速开展，并沿地铁车站结构四周逐渐贯通形成闭合的主裂缝，闭合主裂缝外部区域地表产生较大震陷，闭合裂缝区域(地铁车站结构所在位置)地表隆起，相对向上运动明显，如图13所示。地铁车站结构下层构件水平往复侧向位移较大，灯带振动强烈。试验结束后，取出地铁车站结构可以观察到，结构下层中柱混凝土剥落；侧墙与底板接处产生裂缝，而顶板、中板、底板及侧墙的其他部位未见明显破坏，如图14所示。

图13 地表地震破坏

图14 地铁车站结构的地震破坏

4 结 论

(1)Arias强度与震陷等地质灾害有较好的对应关系。强震作用下地铁车站结构存在改变了土体震陷的分布模式。当峰值振动加速度不超过0.54g时，可采用一次多项式拟合；随着输入峰值振动加速度进一步增大，可采用玻尔兹曼分布式拟合。因此，基于力分布的地铁车站结构抗震设计应充分考虑地震动强度对地基震陷的影响。

(2)强震动作用下地铁车站结构不均匀沉降显著，浅层土体对地铁车站结构约束作用减弱，地铁车站结构与上方土体运动的同步性减弱，在顶层楼板中心位置处出现土结分离现象。

(3)大震作用下地基土水平变形曲线在土层中部偏下位置出现明显的反弯点，从而浅部土层相对位移变化率最大，深部相对位移变化率最小；地基土水平相对位移与土层深度之间可采用三次多项式拟合，两者具有较好的相关性。

(4)地铁车站结构下层最大层间位移角大于上层最大层间位移角；地铁车站结构非规则截面与规则截面的下层最大层间位移角均较大，表明强地震动作用下地铁车站结构下层构件可能出现损伤。因此，地铁车站结构抗震设计中，应重点考虑浅埋地铁车站结构的下层构件，并且考虑截面形式的差异性。