小半径曲线盾构隧道掘进施工地表变形计算

孙捷城，路林海，王国富，周国锋，谭生永，韩 帅

(1.济南轨道交通集团有限公司，山东 济南 250101；2.中国铁路济南局集团有限公司 涉铁工程办公室，山东 济南 250100)

城市地铁隧道受线路布局及周围环境的限制，不可避免地出现小半径曲线盾构施工的情况。相比于直线盾构掘进，小半径曲线盾构施工具有地层扰动加剧、线路两侧地层损失不均匀、地表变形规律复杂等特征。因此，建立小半径曲线盾构施工地层变形计算方法对地表沉降预测及灾害防控具有重要理论指导与实践意义。

目前，关于盾构施工引起的地表变形计算方法主要有：经验公式法，包括Peck公式[1]及修正Peck公式法[2-4]；解析计算法，如文献[5—8]基于相关假设提出了弹性半空间隧道开挖地层变形的解析解；模型试验法，如文献[9—10]通过离心模型试验对盾构施工引起的地表变形规律进行了研究；数值分析法，如文献[11—12]通过数值模拟分析了盾构施工引起的周围地层变形分布规律；Mindlin法，如文献[13—14]利用弹性力学的Mindlin解[15]推导了盾构开挖面推力、盾壳侧摩阻力及刀盘转动摩擦力等引起的土体变形计算公式。

上述研究成果均是针对直线盾构掘进施工，而小半径曲线盾构施工具有线路外侧千斤顶行程较大致使开挖面推力分布不均匀、线路内侧盾壳挤压土体致使摩阻力剧增、线路内侧刀盘超挖较大致使盾尾间隙增大等特征，造成其地表变形规律与直线盾构计算结果偏差较大。且对于曲线盾构施工的地表变形研究多集中于数值模拟的定性分析[16-18]，而对理论计算方法及预测公式方面的研究相对匮乏。

本文综合考虑盾构曲线施工开挖面不均匀附加推力、盾壳不均匀摩擦力、线路两侧盾尾间隙差异对地表变形的影响，基于Mindlin解推导小半径曲线盾构掘进施工引起的地表变形计算公式，通过工程实例进行验证，并探讨不平衡力差异系数及曲线半径对地表变形的影响规律。

1 曲线盾构施工地表变形计算

1.1 曲线盾构掘进力学模型

曲线盾构掘进施工对周围地层的扰动力主要分为：盾构开挖面附加推力q、盾壳与周围土体摩擦力f、盾尾注浆压力p。由此建立曲线盾构推进力学模型如图1所示，图中盾构沿x轴正方向水平掘进，开挖面位于x=0处的yoz平面，盾构直径为D，盾构机盾壳长度为L，隧道轴线埋深为H。

图1 曲线盾构掘进力学模型

在曲线盾构掘进过程中，为了便于分析其施工应力对地层变形的影响，进行如下假设。

(1)土体不排水且为线弹性半无限空间。

(2)盾构推进仅考虑空间位置变化，不考虑时间效应。

(3)盾构曲线掘进过程中，通过设定盾尾千斤顶分组推力及行程实现盾构姿态偏转。根据盾构机设计资料，千斤顶推力分为4组，分组角度为67.5°，90°，112.5°和90°，如图2(a)所示，其中组D与组B推力相同，组A推力大于组C以实现盾构向左侧转弯。

(4)开挖面推力由于千斤顶分组的影响而表现出不均匀性，假定开挖面附加推力以刀盘中线为界线，左侧、右侧分别均匀分布，分别为q1和q2，且q2=ξq1(ξ≥1)，ξ为开挖面推力差异系数，如图2(b)所示。

(5)由于转弯段线路内侧盾壳挤压土体较严重，假定盾壳与土体之间的摩擦力以隧道中线为界线，左侧、右侧分别均匀分布，分别为f1和f2，且f2=ηf1(η≤1)，η为盾壳摩擦力差异系数，如图2(b)所示。

(6)盾尾注浆压力p沿管片圆周径向均匀分布，作用范围为盾尾后方1.2 m，即1环管片宽度。

1.2 开挖面附加推力引起的地表变形

Mindlin[15]推导出弹性半空间内任意一点(x′，y′，z′)处，在竖向集中力Pv和水平集中力Ph作用下的竖向位移w1和w2的计算公式，如式(1)和式(2)，其计算模型如图3所示，图中a为集中力作用点的深度。

图2 曲线盾构受力分析

图3 Mindlin解计算模型

(1)

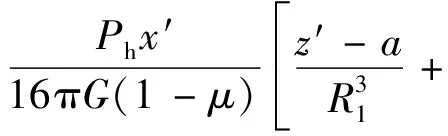
(2)

其中，

式中：G为土体剪切模量(kPa)；μ为泊松比。

对于盾构开挖面正面附加推力，相当于式(2)中的Ph作为刀盘附加推力作用于开挖面上，对其积分得到刀盘圆形面荷载下的地表竖向变形，其计算模型如图4所示。

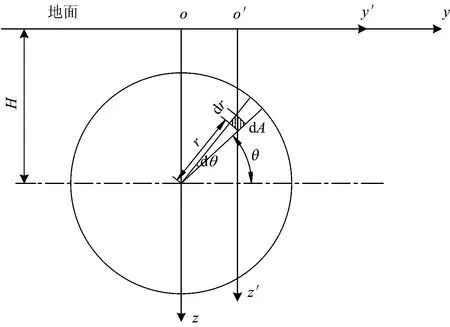
图4 开挖面附加推力引起地层变形的计算模型

图4中，开挖面中任一微元的面积dA=rdrdθ，r为该微元至开挖面中心的距离；θ为该微元与开挖面中心水平面的夹角。该微元所受集中力为dPh=qrdrdθ；为求dPh在坐标系xyz中某一点(x，y，z)处引起的地表竖向位移dw2，需对图3中Mindlin解的x′y′z′坐标系进行坐标系变换为

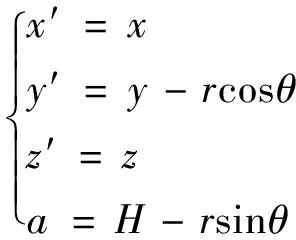
(3)

将式(3)代入式(2)，并根据曲线盾构线路左、右侧附加推力不等而分区间积分，可得开挖面附加推力引起的地层变形wq为

(4)

其中，

由式(4)可知，曲线盾构开挖面附加推力引起的地表变形与推力差异系数ξ有关，其双重积分结果需通过Gauss-Legendre数值积分[19]计算得到。

1.3 盾壳摩擦力引起的地表变形

盾壳摩擦力引起的地层变形计算模型如图5所示，对于盾壳上任一微元的面积dA=Rdθds，R为盾壳半径；s为该微元至开挖面的轴向距离。该微元所受集中力为dPh=fRdθds，进行坐标系变换为

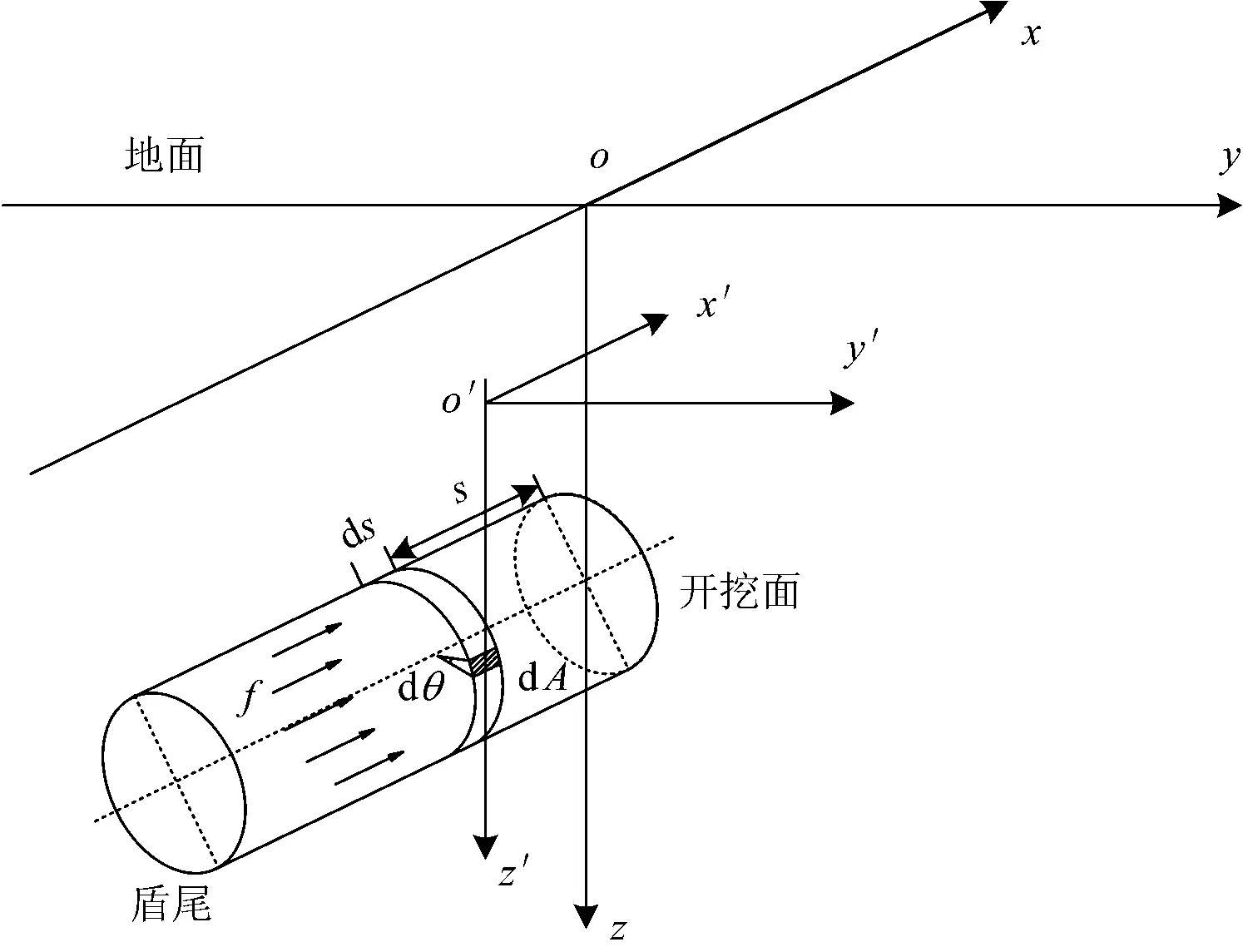
图5 盾壳摩擦力引起地层变形的计算模型

(5)

将式(5)代入式(2)，并根据曲线盾构线路内、外侧盾壳摩阻力不等而分区间积分，可得盾壳摩擦力引起的地层变形wf为

(6)

其中，

Rf1=

Rf2=

Rf3=

Rf4=

由式(6)可知，盾壳摩擦力差异系数η对曲线盾构施工地表变形具有重要影响。

1.4 盾尾注浆压力引起的地表变形

曲线盾构施工线路内侧超挖量较大，盾尾管片与周围土体的建筑间隙较大，需提高注浆量充填盾尾管片外围间隙。在盾尾同步注浆过程中，由于注浆液在间隙中相互贯通，因此假定注浆压力p沿管片圆周径向均匀分布，其曲线内侧超挖量较大引起的地表变形通过第1.5节中地层损失引起的地表变形来计算。

根据林存刚等[14]推导的盾尾同步注浆压力引起的地表位移计算方法，忽略注浆压力p水平分量引起的竖向位移，其竖向分量引起的地表变形wp为

(7)

其中，

Rp1=

Rp2=

式中：S为盾尾注浆段长度(m)，一般取1环管片宽度1.2 m。

1.5 地层损失引起的地表变形

盾构掘进过程中，刀盘超挖将使盾壳与周围土层间产生一定空隙，造成地层损失进而引起地层松动变形。C.Sagaseta[5]假定地层损失从盾构开挖面开始产生，沿纵向呈圆柱体均匀分布，土体变形采用等量径向移动模式，如图6直线盾构所示，在直线盾构掘进过程中，隧道周围地层损失均匀分布，其引起的地表竖向位移wv计算公式为

(8)

式中：Vloss为隧道单位长度的地层损失量，m3·m-1。

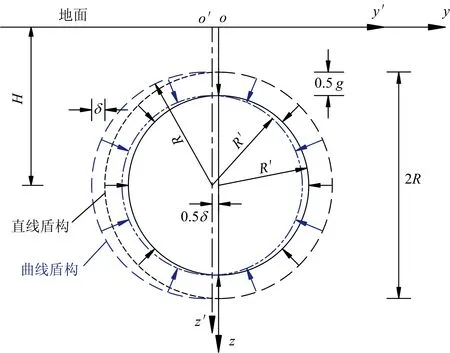
图6 曲线盾构地层损失示意图

由于C.Sagaseta[5]认为盾构掘进地层损失主要位于开挖面处，式(8)仅考虑了开挖面的地层损失。而实际盾构施工，地层损失主要体现在盾尾管片脱出、注浆尚未凝固的阶段，其地层损失集中在盾尾处，因此需要进行坐标系变换为x′=x+L，代入式(8)得

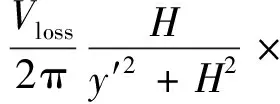
(9)

地层损失量Vloss的计算方法主要分为2种：一是经验方法，根据以往的施工经验确定地层损失率Vl，然后计算得到Vloss=πR2Vl，对于曲线盾构，其掘进施工地层损失加剧，按照常规的地层损失率计算会导致地表变形偏小，故该经验方法不可取；二是根据K.M.Lee等[20]提出的等效土体损失参数g进行计算，如图6所示，在直线盾构施工中，R′=R-g/2，R′为隧道管片结构外半径，则

(10)

而对于曲线盾构，由于小半径曲线盾构掘进线路内侧超挖较大，会使内侧等效土体损失参数g大于外侧，设线路内侧额外超挖量为δ。因此，由盾构直线施工修正得到的盾构曲线施工等效土体损失参数gc为

gc=g+δ

(11)

将式(11)中的gc替代式(10)中的g，可得到曲线盾构的地层损失量为

(12)

根据赵丹[19]关于曲线盾构施工所需间隙的研究，其线路内侧超挖量为

(13)

式中：Rc为曲线盾构线路的曲线半径，m；L1为单段盾壳长度，m；考虑盾构机铰接装置的作用，取L1=L/2。

若采用C.Sagaseta地层损失理论进行计算，必须满足隧道周围地层损失呈圆柱体均匀分布，且位于隧道轴线位置，因此需将坐标系沿y轴进行平移，平移距离为0.5δ(图6)。进行坐标变换y′=y+0.5δ，将其和式(12)、式(13)代入式(9)，得到曲线盾构施工地层损失引起的地表竖向位移wv为

(14)

1.6 曲线盾构施工引起的总变形

综上所述，曲线盾构掘进施工所引起的总地表变形由开挖面附加推力、盾壳与周围土体间摩擦力、盾尾注浆压力以及地层损失引起的地表变形4部分组成，其总变形w计算公式为

w=wq+wf+wp+wv

(15)

将式(4)、式(6)、式(7)和式(14)代入式(15)中，通过Gauss-Legendre数值积分计算得到。

2 工程实例计算分析

2.1 工程概况及参数取值

以济南市轨道交通1号线王府庄站—大杨站区间中的小半径曲线盾构隧道段为例进行计算分析。王—大区间在起讫里程K29+213.84—K29+590.72段以曲率半径Rc=300 m进行小半径盾构曲线掘进，其穿越地层主要为黄土、粉质黏土、细砂土和黏土等。

曲线盾构掘进采用主动铰接土压平衡盾构机，总长L=9.4 m，刀盘外径6.68 m，管片为预制装配式钢筋混凝土结构，外径6.4 m，内径5.8 m，环宽1.2 m，厚度0.3 m，衬砌全环由3块标准块、2块邻接块和1块封顶块构成，错缝拼装。

结合工程资料计算参数取值如下：隧道中心埋深H=19 m，土体平均剪切模量G=12 MPa，重度γ=18.5 kN·m-3，泊松比μ=0.25，黏聚力c=40 kPa，内摩擦角φ=26°，静止侧向土压力系数K0=0.32，盾壳与土体摩擦力f=80 kPa，盾尾同步注浆平均压力p=200 kPa。

整理本工程曲线盾构段的掘进参数监测数据如图7所示。由图可知：盾构土仓压力平均值维持在110～140 kPa，略大于隧道中心处静止土压力，以使开挖面前方地层发生轻微隆起，用于补偿盾尾脱出引起的地层损失，两者求差得到盾构开挖面平均附加推力q=20 kPa；盾构300 m小半径曲线掘进，其曲线段内、外侧土仓压力表现出非对称性，是由于曲线外侧千斤顶油压及行程大于内侧，造成外侧开挖面推力升高，计算分析得到曲线段平均开挖面推力差异系数ξ=1.05，盾壳摩擦力差异系数η=0.90。结合工程经验[18,20]，取等效土体损失参数g=30 mm，代入式(13)计算得到曲线盾构线路内侧额外超挖量δ=18.6 mm。

图7 盾构曲线段土仓压力分布

2.2 纵向地表变形

曲线盾构隧道轴线纵向地表变形的计算值和实测值如图8所示，由图可得如下结论。

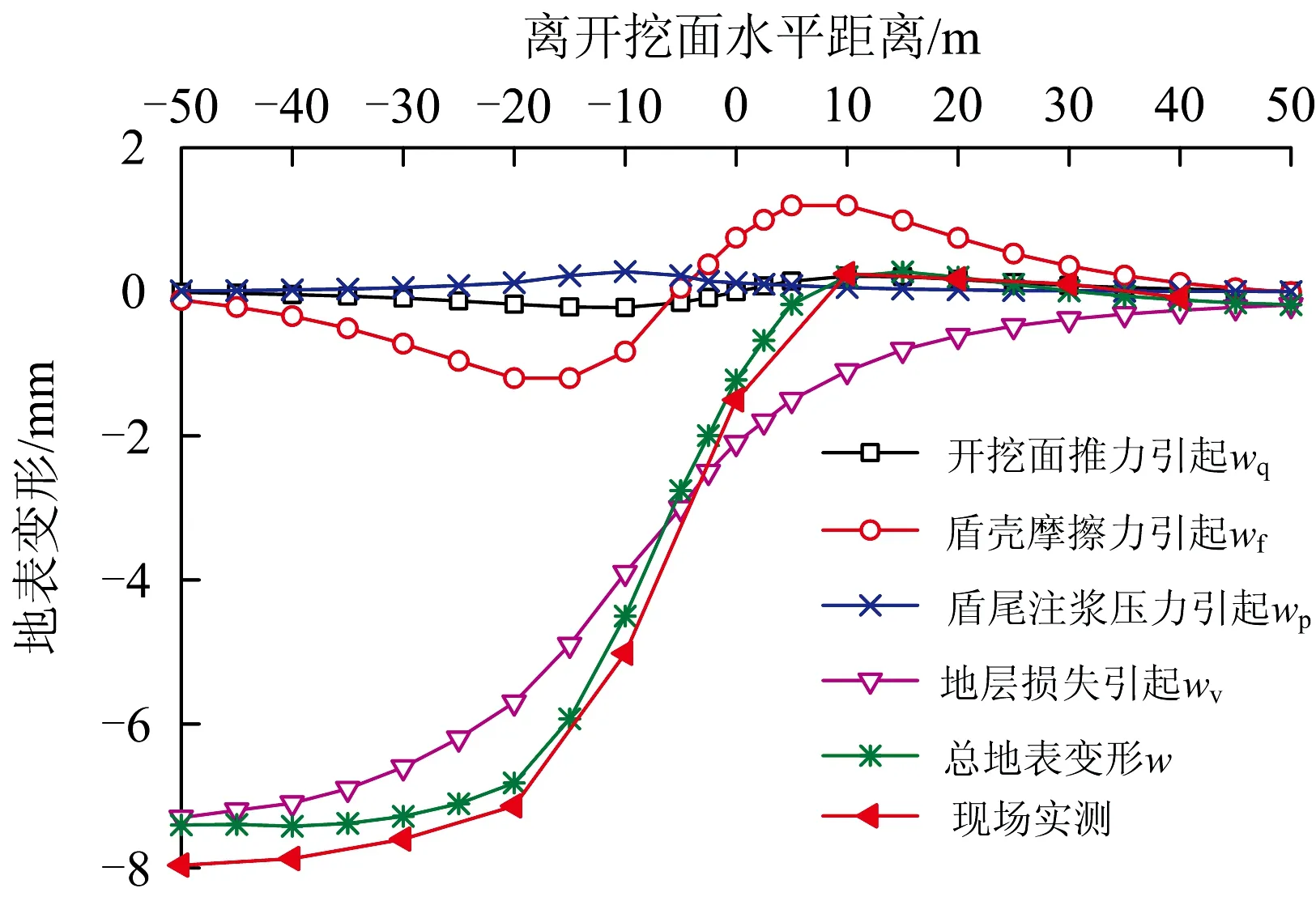
图8 曲线盾构纵向地表变形曲线

(1)开挖面附加推力引起的地表变形沿原点(刀盘位置)呈反对称分布，最大隆起值出现在开挖面前方10 m处，为0.054 mm，最大沉降值对应出现在开挖面后方10 m处，由式(4)可知，wq与开挖面附加推力q1成正比，说明在盾构正常掘进过程中，控制开挖面附加推力在±20 kPa之间，引起的地表变形极小。

(2)盾壳摩擦力引起的地表变形近似沿盾壳中央x=-5 m处呈反对称分布，在其前方呈隆起，最大地表隆起值为1.2 mm，在其后方形成沉降。

(3)盾尾注浆压力引起地表发生隆起，最大隆起值出现在x=-10 m处，即管片脱出盾壳位置，沿该位置向两侧地表隆起逐渐减小，呈对称分布。

(4)总地表竖向变形，在刀盘前方5 m至后方20 m呈现急速沉降阶段，在刀盘前方8～25 m范围呈现轻微隆起，在刀盘后方30 m后变形基本平稳。该理论计算值与现场实测值基本吻合，仅在刀盘后方20 m后具有一定差异，这是由于受扰动土体排水再固结及土体骨架蠕变导致地层沉降持续缓速发展，而本文理论计算假设土体不排水，仅得到了瞬时沉降，因此本文理论计算方法适用于距刀盘后方2L以内距离范围。

2.3 横向地表变形

开挖面前方x=10 m处的曲线盾构横向地表变形曲线如图9所示，由图可得如下结论。

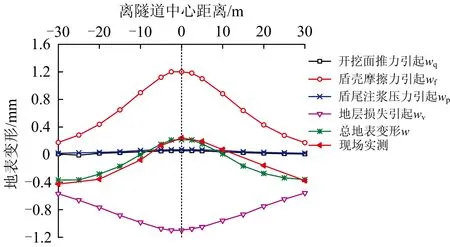
图9 曲线盾构横向地表变形曲线(x=10 m)

(1)开挖面附加推力、盾壳摩擦力、盾尾注浆压力引起刀盘前方地表轻微隆起，在隧道中心线处隆起值最大，沿隧道两侧逐渐减小；其中盾壳摩擦力相对稳定，而开挖面附加推力和盾尾注浆压力与现场掘进控制技术紧密相关，易产生波动。

(2)由于曲线盾构线路两侧盾壳摩擦力差异的影响，致使隧道中心线左侧地表隆起略大于右侧；由于盾构转弯线路内侧超挖较大，造成转弯内侧土体损失量较大，引起地表沉降槽向中心线左侧偏移一定距离。

(3)总地层横向变形呈现出隧道中央地表隆起、两侧沉降的趋势，受曲线盾构两侧不均匀盾壳摩擦力及地层损失的影响，总地表横向变形呈现一定的不对称性；理论计算值与现场实测值较为符合，说明本文计算方法能较为准确地反映开挖面前方地表变形规律。

开挖面后方x=-10和-20 m处曲线盾构横向地表变形曲线如图10所示，由图可得如下结论。

(1)盾尾注浆压力引起该两断面地表隆起，在x=-10 m断面隆起值最大，是由于盾尾同步注浆压力作用于盾尾x=-9.4 m后1环管片(1.2 m)区域，其作用力中心恰好位于x=-10 m断面。

(2)盾壳摩擦力及地层损失因素对地表变形特征起着重要影响，其中地层损失引起的地表沉降分别占两断面总沉降量的86.7%和83.6%，是地层沉降的决定性因素。

(3)两断面的总变形计算曲线与实测曲线吻合度较高，且地表沉降槽均表现出左侧变形略大于右侧变形的规律，较好地反映了曲线盾构施工地层不对称变形的特征。

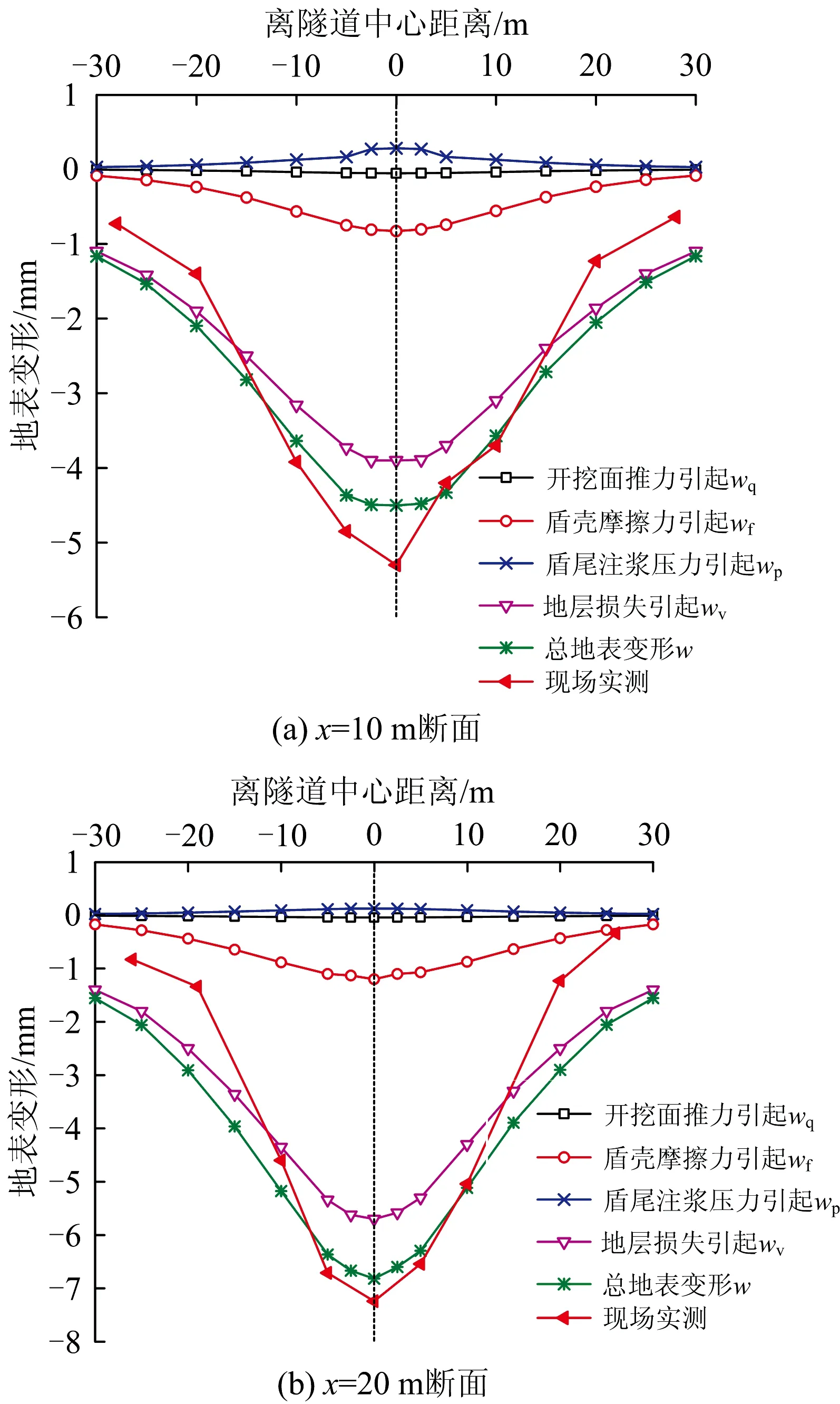
图10 曲线盾构横向地表变形曲线

2.4 计算值与现场实测值的对比

盾构开挖面超过100 m后，地表变形已基本稳定，选取王—大区间Rc=300 m曲线盾构段的地表变形数据离散性较小的5个监测断面(每间隔30 m布设1个监测断面，断面DBC7是盾构进入曲线段的第1个断面)，将其与本文理论计算值进行对比，如图11所示。

图11 各断面实测地表变形曲线

由图11可知：各断面地表变形实测曲线存在一定差异，主要是受隧道地质条件和盾构掘进参数的影响；地表沉降槽曲线总体略偏向隧道中心线左侧，是由于曲线盾构掘进开挖面不均匀推力、盾壳差异摩擦力及曲线内侧地层损失较大造成的；理论计算得到的总地表变形范围较大、较为连续，是由于该预测模型假设地层为线弹性体，与实际略有差异；理论计算值与实测曲线基本一致，验证了本文计算方法的可靠性。

3 曲线盾构地表变形影响因素分析

由理论计算公式与实例计算可知，盾尾注浆压力未引起非对称性地表变形且引起的地表变形量较小，曲线盾构施工产生的非对称性地表变形特征主要是由开挖面不均匀附加推力、盾壳不均匀摩擦力和线路两侧差异地层损失3项因素造成的，因此采用本文计算方法对该3项因素进行影响分析。

3.1 开挖面不均匀附加推力的影响

如图2(b)所示，曲线盾构开挖面左、右两侧附加推力为q2=ξq1(ξ>1)，设定q1=20 kPa，逐步改变ξ值，计算得到开挖面前方10 m处的地表变形曲线，如图12所示。

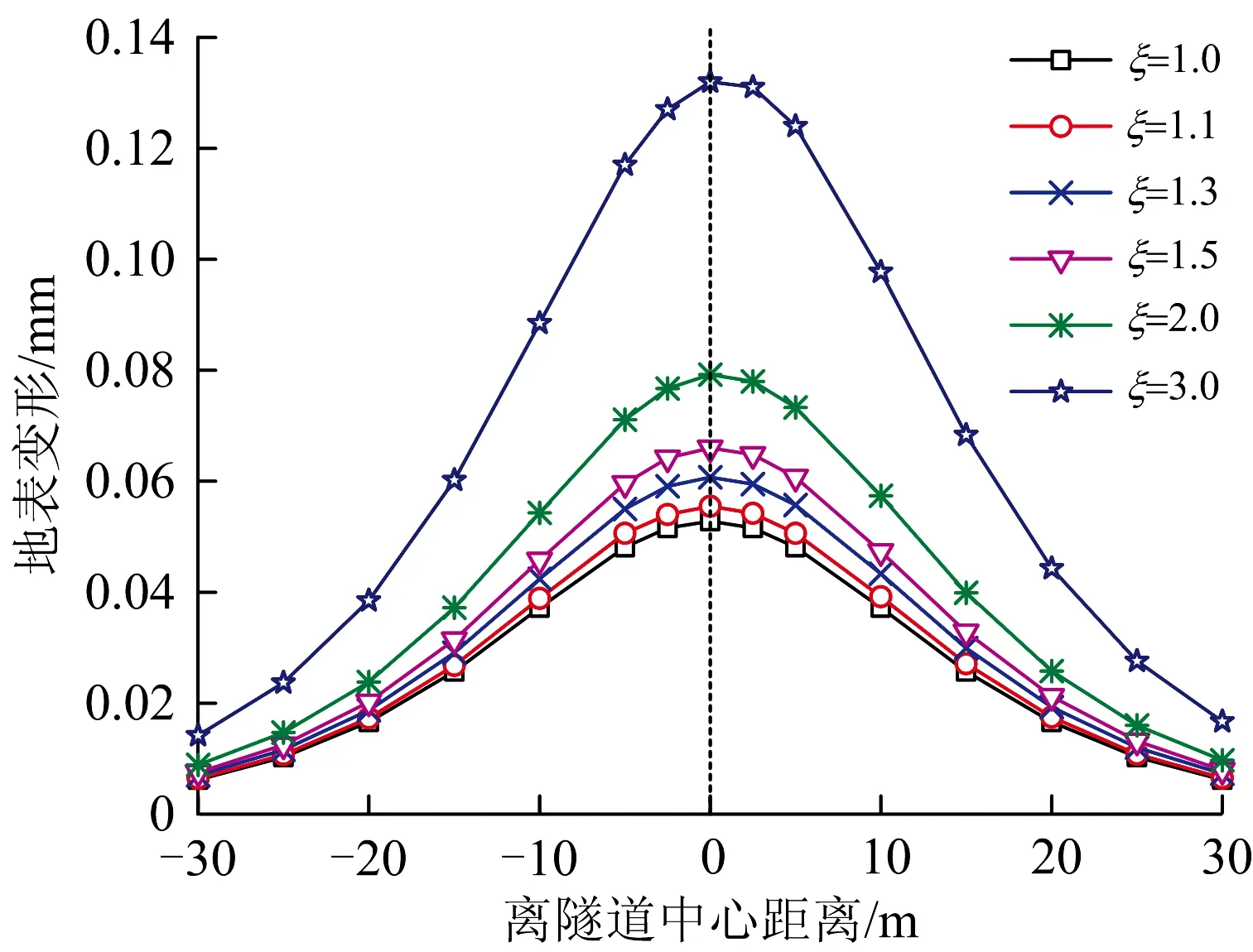
图12 开挖面附加推力对地表变形影响(x=10 m)

由图12可知：随着曲线盾构开挖面推力差异系数ξ的增大，x=10 m断面处的地表隆起逐渐增大，且增幅相对均匀；随着ξ的增大，地表隆起曲线逐渐向右侧偏移，尤其在ξ=4时，隆起峰值点偏离至y=1.1 m处，说明盾构曲线掘进开挖面不均匀附加推力会引起刀盘前方地表隆起增大，隆起峰值向推力较大一侧偏移，且隆起峰值点偏移量随开挖面附加推力差异系数ξ的增大而增大。

3.2 盾壳不均匀摩擦力的影响

如图2(b)所示，曲线盾构盾壳左、右两侧的摩擦力为f2=ηf1(η<1)，设定f1=120 kPa，逐步改变η值，计算得到开挖面后方10 m处的地表变形曲线如图13所示。

图13 盾壳摩擦力对地表变形影响(x=-10 m)

由图13可知：当曲线盾构盾壳摩擦力差异系数η=1时，地表变形曲线近似呈正态分布，峰值沉降位于隧道中线，向两侧逐渐减小；随着η的减小，地表变形逐渐减小，且地表沉降槽逐渐向隧道左侧偏移，说明盾构转弯时两侧盾壳摩擦力的差异会引起地表沉降槽向转弯内侧偏移。

提取图13中不同η值时的地表峰值沉降及沉降槽中心偏移量，如图14所示，由图14可以得出如下结论。

(1)地表峰值沉降量Δ随着η的减小呈线性递减，其拟合公式为

Δ=-0.581η-0.582

(16)

(2)沉降槽中心偏移量I随着η的减小而显著增大，是关于盾壳摩擦力差异系数η的二次函数，其拟合公式为

I=0.890η2-2.448η+1.564

(17)

图14 不同盾壳摩擦力差异系数时的地表沉降槽特征

3.3 地层损失的影响

盾构曲线掘进过程中，转弯线路内侧超挖较大，造成内侧地层损失大于外侧。计算得到开挖面后方30 m处由地层损失引起的地表变形情况，如图15所示。

图15 地层损失对地表变形影响(x=-30 m)

由图15可知：随着盾构掘进曲率半径Rc的减小，盾构曲线掘进线路内侧超挖量逐渐增大，地层损失逐渐加剧，引起地表沉降量增大；地表沉降槽偏移量随Rc的减小没有明显变化，这是由于地铁隧道受限于运营期列车高速运行对轨道的磨损，其转弯曲率半径一般不小于200 m，当Rc=200m时，线路内侧额外超挖量δ=28 mm，引起的沉降槽偏移量相对较小。

4 结 论

(1)基于Mindlin解，考虑曲线盾构线路两侧不均布受力及超挖特征，推导得到曲线盾构施工引起的开挖面附近地表变形计算公式，并通过工程实例分析，验证了本文计算方法的有效性和可靠性。

(2)开挖面附加推力引起的纵向地表变形沿原点呈反对称分布，最大变形值距离开挖面约10 m；盾壳摩擦力引起的纵向地表变形沿盾壳中央呈反对称分布，在其前方呈现隆起，后方形成沉降；盾尾注浆压力引起的纵向地表隆起在管片脱出盾壳位置形成峰值，向两侧呈对称分布且逐渐减小。总地表竖向变形在刀盘前方5 m至后方20 m呈现急速沉降阶段，在刀盘前方8～25 m范围呈现轻微隆起，在刀盘后方30 m以后变形基本平稳。

(3)盾构小半径曲线掘进横向地表变形沿隧道轴线呈非对称性分布，地表沉降槽中心偏移量随着线路两侧开挖面附加推力及盾壳摩擦力差异的增大而增大；地层损失及地表沉降随着盾构曲线半径的减小而逐渐增大。