关于一道初中几何试题的多种解法
唐小淋 任小清 何甜 杨婷

【摘要】几何与图形是初中阶段四大板块之一,在整体知识结构中有着举足轻重的作用.本文主要对一道初中几何试题的第一小问给出多种证明方法,从不同角度出发,有助于提升学生的发散性思维.
【关键词】面积相等法;构造全等法;倍长线段法;翻折图形法;三角函数法
几何与图形是中考命题的热点内容之一,所占分值比重较大,尽管不同省份不同地区知识点比重分布不一,但几何部分在中考中的比重几乎占到30%到40%,可见几何与图形在初中阶段的重要性.而关于几何题的证明及其解法往往不止一种,但却有一定的规律可循,因此,我们在平时的学习中,应善于总结发现一类题目的解题方法.同时,这也就要求我们教师平时在上课中应尽可能多地为学生提供不同的思路,这也有助于培养学生的发散性思维和创造性思维,激发学生对数学学习的兴趣.
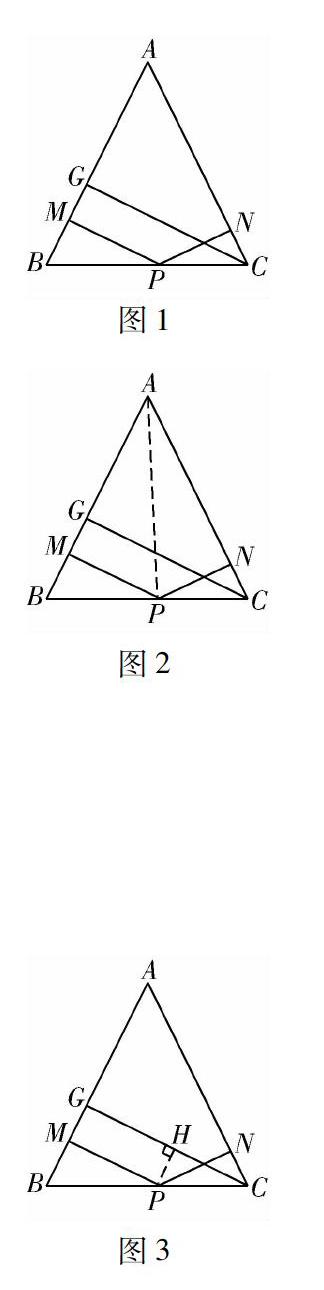
题目如图1所示,已知△ABC中,AB=AC,点P是BC上一点,PN⊥AC于点N,PM⊥AB于点M,CG垂直AB于点G.CG,PM,PN之间有什么数量关系?证明你的猜想.
CG=PM+PN.
方法一面积相等法
证明(如图2所示)连接AP.
∵S△ABC=12AB·CG.
同时,S△ABC=S△ABP+S△APC=12AB·PM+12AC·PN.
∵AB=AC,∴S△ABC=12AB·CG=12AB(PM+PN),
∴CG=PM+PN.
方法二构造全等法
证明(如图3所示)过点P向CG作垂线,垂足为点H.
∵PM⊥AB,CG⊥AB,PH⊥CG,
∴∠PMG=∠MGH=∠GHP=90°,
∴四边形MGHP为矩形,MP=GH.
∵PH∥AB,∴∠HPC=∠ABC.
又∵AB=AC,∴∠ABC=∠ACB,
故∠HPC=∠NCP.
∵PH⊥CG,PN⊥AC,∴∠PHC=∠CNP=90°,
而PC=CP,∴△HPC≌△NCP(AAS),
∴PN=CH,因此,CG=PM+PN.
方法三倍长线段法
证明(如图4所示)延长MP,使PQ=PN,连接CQ.
∵AB=AC,∴∠ABC=∠ACB.
∵PM⊥AB,PN⊥AC,
∴∠PMB=∠PNC,
∴∠BPM=∠CPN.
又∵∠BPM=∠CPQ,
∴∠CPN=∠CPQ,
而PC=PC,PN=PQ,
∴△PNC≌△PQC(SAS),
∴∠PNC=∠PQC=90°.
又∵∠QMG=∠MGC=∠MQC=90°,
∴四邊形MQCG为矩形,∴MQ=CG.
因此,CG=PM+PN.
方法四翻折图形法
证明(如图5所示)将△PNC绕线段PC翻折得到△PRC,
∴△PNC≌△PRC,
∴PN=PR,∠NCP=∠RCP.
又∵AB=AC,∴∠ABC=∠ACB,
∴∠ABC=∠RCP,故CR∥MG.
∵PM⊥AB,CG⊥AB,∴PM∥CG,
∴∠BPM=∠BCG.
又∠BPM=∠CPN,而∠NPC=∠RPC,
∴∠BCG=∠RPC,∴PR∥CG.
∵PR∩PM=P,∴RM∥CG,∴四边形MGCR为矩形.
∴MR=CG,∴CG=PM+PN.
方法五三角函数法
证明设BP=a,CP=b,∠ABC=α.
∵PM⊥AB,PN⊥AC,CG⊥AB,
∴∠PMB=∠PNC=∠BGC=90°.
在Rt△BMP中,PM=BP·sinα=a·sinα.
又∵AB=AC,∴∠ABC=∠ACP=α.
在Rt△PNC中,PN=PC·sinα=b·sinα.
在Rt△BGC中,CG=BC·sinα=(a+b)·sinα,
∴CG=PM+PN.
以上给出了本题的五种证明方法,其实对此题还有其他的解法,例如,将方法三中的辅助线改为:延长MP,过点C向MP的延长线作垂线交于一点O,证明△PNC≌△POC即可.其实,对这类线段的和(差)问题证明的题目,有一个最基本的解法,就是可通过“截长补短法”来实现对线段数量关系的证明.在平时的教学中,教师应注意培养学生的求异思维,即一题多解的能力,可以引导学生从不同的角度、各种途径探求解题方案,这样既可展现学生的思维过程,增加教学透明度,又有利于拓宽学生的思维,增加学生思维的灵活性与广阔性,激发学生的创新意识.同时,对解同一道题目,若选择的思维起点不一样,其解决问题的复杂程度也不一样,因此,我们要善于引导学生去分析比较哪一种方法更具有优势,并灵活调整,使学生学起来游刃有余.
【参考文献】
[1]蔡斌.启发学生思维突破初中几何学习难点[J].北京教育学院学报(自然科学版),2014(4):48-53.

