在不等式教学中如何培养学生的探究思维能力

陈永恺 绵阳师范学院 四川绵阳 621000

绪论

学生的学习能力和探究思维能力的培养是数学教学的重要目标之一，这也就是培养创新型的人才.近几年，经常会有学生出现“不教的话就不会，遇到新的问题也不会”的情况.也就是说，学生只懂得老师在课堂上所讲的题目与知识点，对于其他的拓展内容或者是新颖的题目，学生都想不到如何去解答.

新一轮国家基础教育课程改革的一个重要而具体的目标，就是要改变旧的学习方式，倡导学生主动参与的探究性学习.因此，在数学教学中怎样培养学生的探究思维能力，是一个被广泛关注的课题.所以，本文将从不等式的教学中来拓展学生的探究思维能力.

1 通过教材，引导学生探究

1.1 不等式在中学教学中的地位

不等式与数、式、方程、函数、三角等内容都有密切的联系，讨论方程或者方程组的解的情况的时候，对函数的定义域、值域以及许多方面的研究以及对线性规划的研究中，都会很经常的用到不等式.同时，不等式在解决各类实际问题中也有很广泛的应用.由此可见，不等式在中学数学中占据了十分重要的地位.这对于要进一步研究数学是必不可少的.

1.2 通过教材中的内容来教学

1.2.1 注重对概念的教学

许多学生对这种基础的概念并不是特别的了解，只是知道个大概的模样.类似于“3>0”，肯定会有很多学生会说这就是不等式.这就是对概念的不清楚，概念中明确的指出，不等号两边是整式.连最基本的都会弄错的话，就更不用说什么再去探究了，只会错上加错.许多学生可能会认为，数学是理科，不像文科那样有那么多的条条框框，有那么多的概念需要背诵，所以才会对概念掌握没有那么深.但是恰恰相反，正是因为是理科，概念的东西虽然不多，而且很零碎，但是如果有一个概念你记错了的话，可能会导致接下来的很多概念你都会推导错误.

1.2.2 通过教材的例题来培养学生的探究能力

课本上的例题虽然有特例性，但是例题同时也是新学到的知识的运用，课本上的答案通常与本课时所学的知识点相关联，学生也就自然而然的与本节内容相联系，这样反而会阻碍了学生思维的全面发散.而如果在例题的教学中也采用探究的方式，就能够解决学生的这一种思维定式.

例如：

（1）用篱笆围一个面积为100m的矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短，最短的篱笆是多少？

（2）一段长为36 的篱笆围成一个矩形菜园，问这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

就取（1）来说，在学生们知道了用这种方法能解决这样的问题的时候，我们是不是可以让他们用同样的方法，不一样的思路来解决这问题.就比如我可以不设长为x，宽为y.我可以根据题目的已知条件，来设长为x，宽为100/x.这样也可以解答这样的问题，但是就不是从刚刚那个角度来切入了.

1.2.3 将教材中的定理的特殊条件推广到一般情况

在教材中有许多的定理和结论都是在特殊情况下成立的，我们可以让学生们试一试在一般情况的推广下是否能够成立.

例如我们所学过的不等式a+b≥2ab，可以得出a+b≥-2ab，a+b≥2∣ab∣,a,b∈R类似这样的推论，我们都可以让学生们自己来尝试，既可以增强学生的理解能力，也能提高学生们的思维的活跃能力.从而提高学生学习的积极性.

2 利用题目的错解，来训练学生的批判思维，激发求知欲

学生刚学习不等式的时候，肯定会有很多的概念性的理解不清楚，经常造成解题出错.我们可以通过对错误解答的分析，寻找问题的根本，增强学生对概念的理解能力，以及自身的思维能力.

3 通过一题多解来培养学生探究能力

在数学解题的教学中，教师应该要侧重在指引学生自己发现的方面.通过侧面引导，启发学生从不同的角度挖掘问题，从各个层面去剖析问题.从而探索问题实质的变与不变.

3.1 改变学生固定的思维模式，同时扩宽学生的认知

一题多变在拓展学生的探究能力上有很大帮助，通过对题目的变化，让学生不仅能“温故”，同时还能“知新”.

在学生掌握这道题目的解题过程以及解题思路之后，教师可以引导学生根据命题的条件和结论及一般到特殊、特殊到一般的方法进行引申推广.

如：

（1）保留条件，深化结论

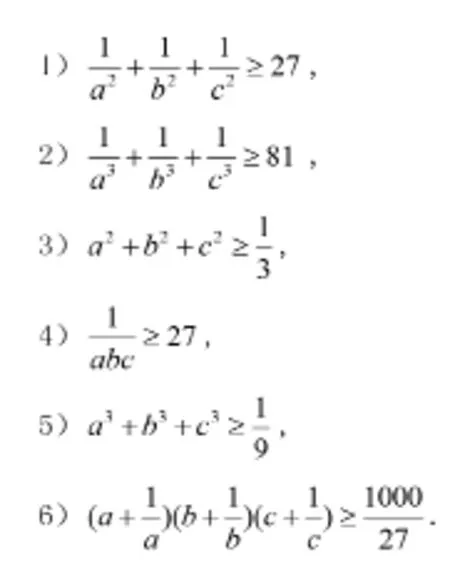
（2）采用一般到特殊的思路，从上面的式子中引进常数.

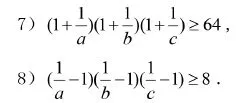
结束语

本文主要讲了如何从不等式中培养学生的探究能力.在现阶段的应试教育下，许多学生只会死记硬背，缺少自己的思想.在数学教学中，教师的任务不仅仅是传授知识，更应该通过知识这个介质来培养学生的探究思维能力.“创新是一个民族进步的灵魂，是一个国家兴旺发达的不竭动力”.数学的创新观念不容易形成，但是一旦形成，就会变的根深蒂固，无法撼动.这就需要教师们的不懈努力了.