R&D投入真的能提升企业创新绩效吗——来自广义倾向得分匹配的证据

周衍平（博士生导师），耿芳菲，陈会英（博士生导师），吴国庆

一、引言

十九大报告强调，创新是引领发展的第一动力，是建设现代化经济体系的战略支撑，要把加快建设创新型国家作为我国现代化建设的战略性举措。为此，企业要想在不断加剧的市场竞争中求得生存和发展，就必须提高自身创新能力，掌握核心技术，不断实现技术创新，打造自身的优势以及培养雄厚的综合实力[1]，为加快创新型国家建设贡献力量。研究与开发（Research and Development，R&D）作为技术创新的重要环节之一，是企业发展的重要创新来源和创新的决定因素，合理配置科技资源可以提高企业设备和工艺的技术水平，给企业带来直接的经济效益[2]。

R&D 投入和企业创新绩效之间的关系已经得到了国内外相关学者的广泛关注。该类研究最早起源于发达的工业国家，其中大部分认为R&D 投入与企业创新绩效显著正相关。不过现有研究并没有达成一致的观点，R&D投入对企业创新绩效的影响或多或少会受到其他因素的干扰，而现有文献对于这些影响因素的控制还存在一些不足，这就带来了研究结果的不确定性。鉴于以上背景，本文选取我国2010 ～2017 年中小板企业作为研究样本，使用广义倾向得分匹配（Generalized Propensity Score，GPS）法，在“反事实”框架下，通过进一步控制“自选择效应”和其他因素的影响，深入探析R&D 投入对企业创新绩效的影响。

R&D投入真的能够提升企业创新绩效吗？本文通过GPS方法，不仅可以在“反事实”框架下明确R&D投入对企业创新绩效的影响，还能探讨不同R&D投入强度对企业创新绩效影响的动态变化过程，从而发现R&D 投入的理想区域。另外，通过研究，还能明确对于同一个企业进行不同强度的R&D 投入与不进行R&D 投入而言对创新绩效的影响具有何种区别，以帮助企业管理者们在是否进行R&D 投入之间该如何做出正确的决策提供实证经验。

二、文献综述

众多国内外学者都对R&D 投入对企业创新绩效的影响进行过研究，以期企业能够通过合理的R&D投入提高技术成果产出，最终实现提高企业生产率的目的。Raymond 等[3]使用荷兰和法国制造业企业的数据，通过四个非线性动态联立方程描述了从R&D 到创新绩效，再从创新绩效到生产率的转换过程，最终明确了企业R&D 投入对提高生产率所发挥的关键性作用。余淑秀、卢山冰[4]发现R&D投入能够显著提升我国汽车制造业的技术创新能力，并且还能正向调节FDI 对企业创新绩效的促进作用。王素莲、阮复宽[5]进一步研究发现，企业家越偏好承担风险，R&D投入与公司绩效之间的正相关关系越强，这对进一步明确R&D 投入与企业绩效关系异质性的作用机理具有重要的理论意义。随着研究的深入，部分学者发现在一些因素对企业创新绩效的影响中R&D 投入还起到了中介作用。如丘东等[6]和高雨辰等[7]分别验证了政府的R&D 投入和研发补贴对地方或企业创新绩效的作用是通过企业R&D实现的，杨林等[8]发现高管团队海外行业经验对企业创新绩效的影响完全是通过R&D 投入这一中介变量实现的，陈岩等[9]认为家族所有权会通过R&D 投入的中介机制对创新绩效产生影响。不过，以上研究却忽视了R&D 投入对创新绩效可能并不是简单的非线性影响。王康、周孝[10]通过实证检验发现，随着R&D 强度或企业规模的增大，持续的R&D 投入将对技术创新绩效产生非线性影响，即呈现出“负向——正向——负向”的变化趋势。同样，周密等[11]、易靖韬等[12]也认为R&D 投入将对创新绩效产生非线性影响。

不过，现实中创新绩效高的企业往往倾向于更高的R&D 投入，也就是创新绩效高的企业本身R&D 投入就高，即存在“自选择效应”。而“自选择效应”会带来内生性问题，以往学者在研究R&D 投入对企业创新绩效的影响时往往忽略了这一问题。同时，研究R&D 投入对企业创新绩效的影响，应当排除其他因素对R&D 投入和企业创新绩效的影响，如企业规模、企业的偿债能力和盈利能力等均会对R&D 投入和企业创新绩效产生影响。只有控制了其他因素的干扰，才能更准确地研究R&D 投入对企业创新绩效的影响。而对于已经进行一定R&D投入的企业不能直接验证其不进行R&D 投入的情况，即“反事实”。

匹配方法是一种较好地控制“自选择效应”和其他因素影响的方法，可以在“反事实”分析的框架下，选出主要特征最接近的企业个体进行比较，从而可以较准确地分析R&D 投入对企业创新绩效的影响，即净效应。但是由Rubin 等[13]提出的倾向得分匹配（Propensity Score Matching，PSM）方法只适用于0 或1 的二值型处理变量，即只能分析R&D投入与否（有为1，没有为0）对企业创新绩效的影响。值得注意的是，R&D 投入对企业创新绩效的影响，不仅取决于企业是否有R&D 投入，而且R&D 投入强度的差异对企业创新绩效的影响是有显著差别的，这就需要进一步考虑企业的R&D 投入强度对企业创新绩效的影响。如果仅仅研究是否有R&D 投入对企业创新绩效的影响，将会严重低估R&D 投入带来的效应。

Imbens[14]和Hirano等[15]进一步拓展了PSM方法，将“反事实”分析框架处理变量扩展到多元变量或者连续变量的范畴，提出了利用GPS 方法来捕捉不同处理强度下潜在结果的差异，弥补了PSM方法的不足。GPS 方法不仅能够较好地克服“自选择效应”，还能较好地控制其他因素对R&D 投入和企业创新绩效的影响。此外，Hirano 等[15]还进一步建立了剂量反应函数，用以描述不同的处理变量所对应结果变量的条件期望，即可以进一步研究处理变量对结果变量的动态影响，利用该函数可以在王康、周孝[10]研究的基础上进一步分析和验证R&D投入对企业创新绩效的影响是否是非线性的。

GPS 方法已经得到了广泛应用。Kluve 等[16]用GPS方法以德国的官方数据为样本研究培训时间的长短对员工再就业的影响，发现培训时间在100 天之内再就业率呈上升趋势，100 天之后再就业率无明显变化。Sheldon、DeShazo[17]研究了 2010 ～ 2013年间美国加利福尼亚州允许使用插电式电动汽车免费占用高拥堵车道的政策效果，发现该政策导致了插电式电动汽车购买登记数量的增加。国内学者近些年来也开始使用GPS 方法研究企业出口的经济后果，正是因为该方法的使用，学者们才能更加方便地研究非线性因果关系。史青[18]研究发现企业出口确实能显著提高员工工资，但是这一因果关系只在样本的某些子区间成立，并且企业的出口强度与员工工资呈现“倒U型”的非线性关系。陈勇兵等[19，20]发现企业出口强度与企业生产率和销售额增长率之间也呈现“倒U型”的关系。除企业出口经济后果的研究之外，汤学良等[21]、陈梅等[22]使用GPS方法研究发现，培训投入、进口中间产品质量分别与企业生产率呈“倒N型”“U型”关系。

以上学者对GPS 方法的探讨为本文奠定了计量基础，以往学者在使用GPS 方法时还或多或少存在一定的缺陷：其一是忽视了GPS 方法使用后对匹配变量的平衡性质假定的检验；其二是GPS 方法同PSM 方法一样，均需要满足共同支撑假定，但是目前的文献却极少提及GPS 方法的共同支撑假定该如何检验。因此，本文结合国内外学者的相关研究，试图给出一个规范的GPS方法的使用框架。

三、数据来源与变量设定

（一）数据来源

本文从国泰安数据库选取2010 ～2017 年中小板企业作为研究样本。之所以选择中小板企业，主要是考虑到中小板企业大多处于生命周期的初创期或者成长期，其科研创新能力较强，中小板企业在创新和研发支出方面披露的信息最为完整。为了研究结果的稳健性和准确性，本文对样本进行如下处理：

首先，考虑到金融类企业本身的特殊性，按照证监会2012 版行业分类代码，将行业代码以J 开头的样本企业剔除；然后，为了研究结果更加稳健，剔除ST 和∗ST 类企业；最后，本文还剔除了专利申请数量、R&D投入出现缺失值的样本。最终，共得到4325个样本。样本具体分布情况如表1所示。

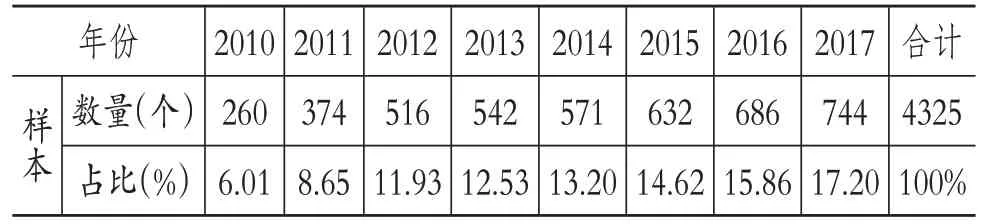
表1 样本分布情况

同时，为了使研究结果更加稳健，本文还进一步对所有的连续变量在1%分位数以下和99%分位数以上进行了缩尾处理，以消除异常值带来的影响。

（二）变量设定

1.处理变量。学者们主要采用两种方式衡量企业的R&D 投入：一种是绝对指标，即R&D 的支出总额；另一种是相对指标，即R&D 支出/营业收入，亦称R&D 投入强度。为了避免企业规模带来的影响，本文采用相对指标，记为RD。由于不同企业R&D 投入存在显著差异，且多数企业R&D 投入较低，导致R&D投入分布是严重有偏的，如图1所示。借助分数对数模型进行调整，由此需要将处理变量的取值限定在0 ～1 之间，因此本文在对变量RD 进行缩尾处理的前提下，将RD 的最大值标准化为1，然后用其他RD 除以该最大的RD 值，这样就保证了RD的取值在0 ～1之间。

图1 R&D投入分布

2.结果变量。现有研究对企业创新绩效的衡量主要包括净资产收益率、专利申请数、新产品的销售收入等。考虑到专利更能反映一个企业的创新成果，且专利申请数可以在很大程度上克服不同企业之间创新成果受到工作效率、偏好等方面因素的影响，更具有一致性和公正性，本文借鉴张信东等[23]、徐维祥等[24]的研究方法，采用专利申请数来衡量企业创新绩效，记为APP。

3.匹配变量。考虑到匹配变量应该既要与处理变量相关，也要与结果变量相关，以更好地满足条件独立性假设[20，21]。对此，本文借鉴现有研究[1，25-28]选取以下变量作为匹配变量：

政府补助，该项目主要包括财政拨款、税收返还和各种财政补贴（比如研究开发补贴、财政贴息和政策性补贴等），该数据主要披露于上市公司财务报表附注，本文以政府补助总额的对数值来衡量，记为SUB；高管激励，该项目主要包括企业对高管的薪酬激励和股权激励，本文借鉴尹美群等[28]和苗淑娟等[29]的做法，用董监高持股总数与公司总股数的比值来衡量，记为MHSR；股权集中度，以第一大股东持股总数与公司总股数的比值来衡量，记为FHSR；企业规模，以企业总资产的对数值来衡量，记为SIZE；资本密度，即企业固定资产总额除以员工人数，然后取对数，记为CD；偿债能力，以企业的资产负债率来衡量，即企业的总负债除以总资产，记为LEV；盈利能力，以企业的资产收益率来衡量，即企业的净利润除以总资产，记为ROA。以上所有的变量设定情况如表2所示。

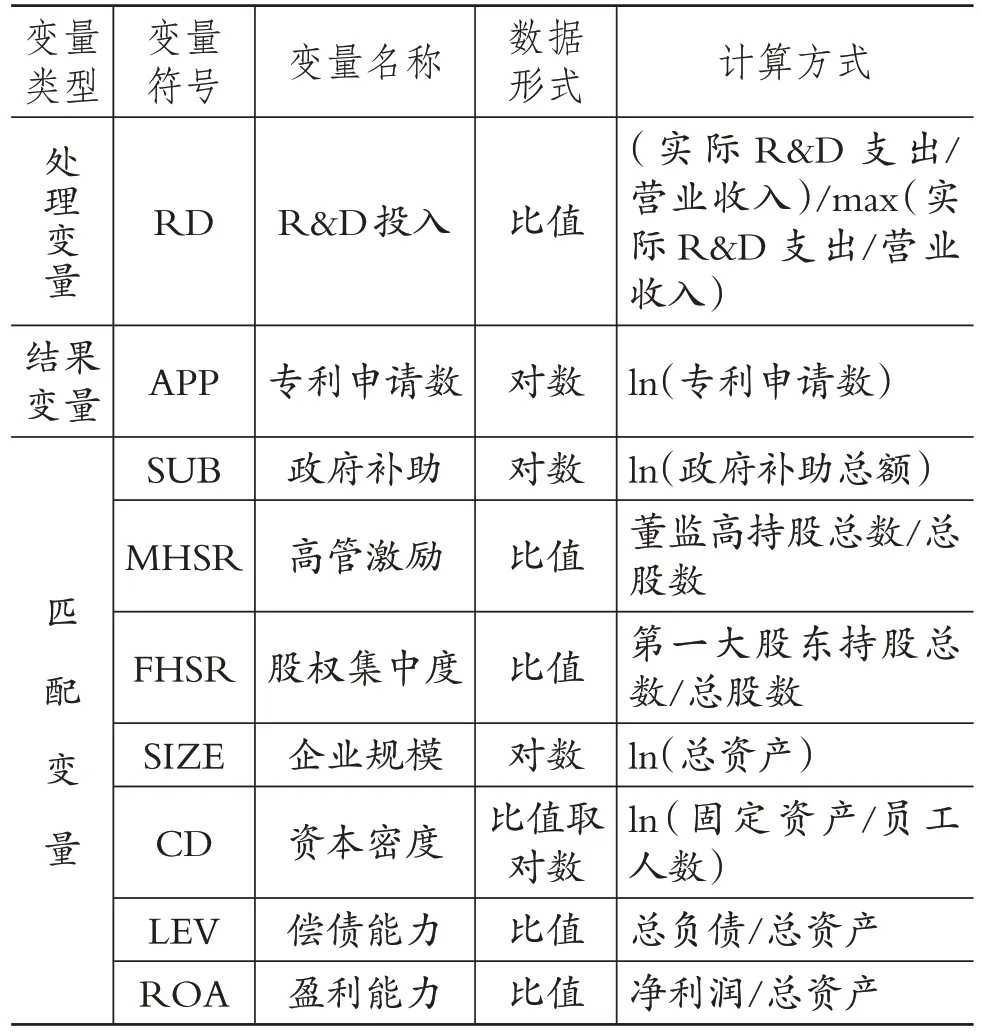
表2 各变量设定

四、实证分析

（一）描述性统计

为了初步统计分析R&D投入对企业创新绩效的影响，测算出各年度不同R&D 投入在样本中所占的比例及其对应的企业创新绩效的信息，并汇总列出全样本的信息（详见表3）。表 3 显示，随着 R&D 投入的增加，企业创新绩效均值呈现出先增大后减小的趋势，最后在（0.8，1］区间又突然增大。在（0.8，1］区间的是少数在样本中所占比例较小的新型高新技术企业，这类企业创新需求和动力十分巨大，R&D投入较多，同时在国家政策的引领下不断创新，取得的成果显著。可见，R&D投入达到一定程度之后可能又会促进企业创新绩效提高。

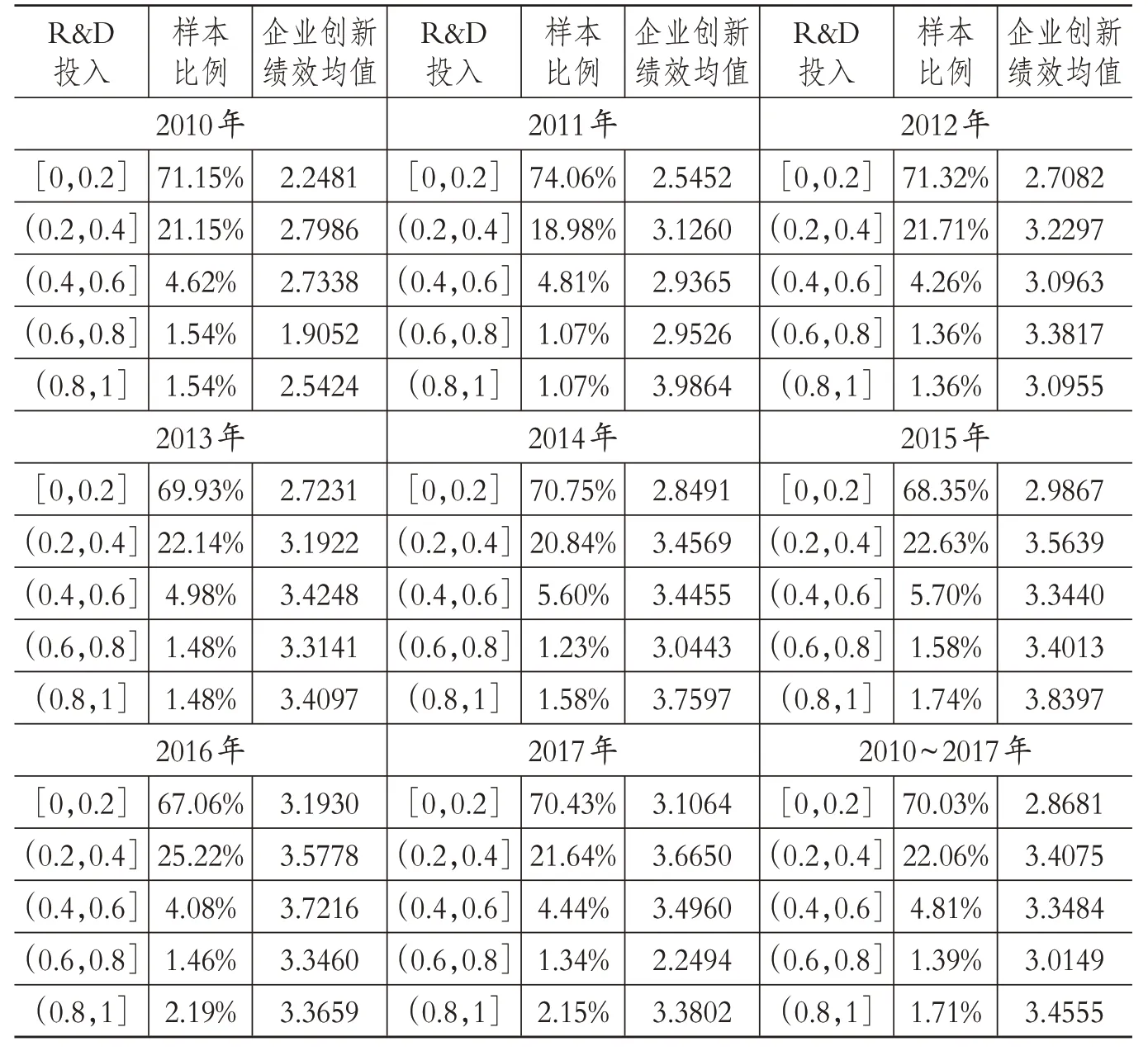
表3 R&D投入强度与企业创新绩效的初步统计分析

为了验证上述猜测，本文将全样本R&D 投入在（0.8，1］区间的样本筛选出来，共有74 家企业，几乎都是新型高新技术企业，如表4所示（表中只列示了部分企业，其中所占比例指的是在74家企业中所占的比例）。表4 中样本企业占74 家企业的七成左右，都是软件、信息技术和电子设备等高新技术企业，与人工智能、互联网密切相关。

若忽略这类新型高新技术企业带来的影响，随着R&D 投入的不断增大，企业创新绩效均值呈现出先增大后减小的走势，因此初步判断R&D 投入对企业创新绩效的影响为“倒U型”。

表5给出了变量的描述性统计结果。可以看出，处理变量RD 最小值为0.0038，最大值为1.0000，这是前文为了确保R&D 投入取值在［0，1］之间特别处理过的结果。结合RD 的均值和中位数来看，R&D 投入的分布是严重有偏的，且为正偏峰分布（右偏），说明我国中小板企业R&D投入大部分处于中低水平。如2012 年我国高技术R&D 投入仅占工业总产值的1.69%，远远低于同期的日本和美国[30]。结果变量专利申请数量反映了企业的创新绩效，由于本文对专利申请数量进行了对数处理，所以出现最小值为0的原因是该企业专利申请数为1。从均值3.0222 来看，我国中小企业创新绩效总体水平并不低，并保持了良好的发展势头，这与我国“创新驱动发展战略”密切相关。从统计量来看，政府补助基本符合正态分布，可以看出政府对我国中小企业的补助还是相对合理公平的；高管激励，即高管持股比例最小值为0，最大值为72.5850%，表明我国中小企业高管持股存在很大差异；股权集中度均值为34.1988%，最小值为9.5900%，最大值为70.5300%，我国中小板企业股权集中度极差较大，但是平均水平处于30%～40%区间，说明既有股权分散企业，又有股权集中企业；企业规模最小值20.0930，最大值24.0550，显示我国中小板企业资产规模差距并不大，这主要是由中小板挂牌企业的规定所限制；资本密度的均值为12.3691，可以看出我国中小板企业资本密度较高，即人均固定资产处于较高水平；偿债能力均值为0.3530，说明我国中小板企业总体来说，平均负债尚处于合理水平；盈利能力最小值为-0.1063，最大值为0.2235，盈利能力具有较大差异性，这可能是当前经济形势下部分中小企业融资难、融资贵问题所致。

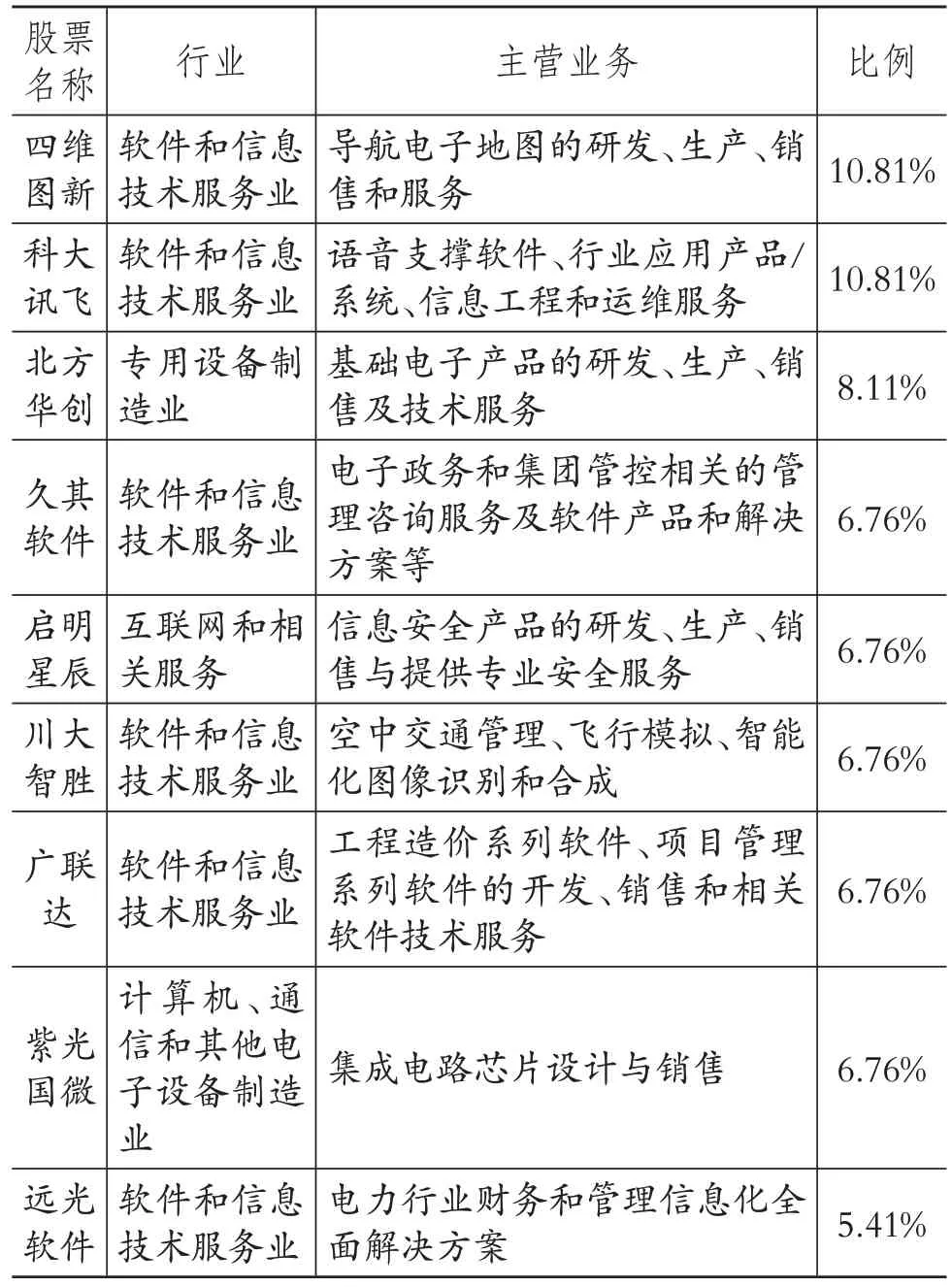
表4 部分R&D投入在（0.8，1］区间的企业概况

（二）R&D投入对企业创新绩效的影响

运用GPS 方法估计R&D 投入对企业创新绩效的影响分为三步：估计处理变量R&D 投入的条件分布并计算GPS 得分、估计结果变量企业绩效的条件分布、估计剂量反应函数和处理效应函数。

表5 变量的描述性统计

1.估计处理变量R&D投入的条件分布。

（1）R&D投入的条件分布。Hirano、Imbens[15]提出的GPS 方法要求处理变量必须是正态分布。但是根据前文分析，R&D 投入是严重有偏的（如图1 所示），因此需要采用分数对数模型来估计R&D投入的条件密度函数。

本文选取财政补助（SUB）、高管激励（MHSR）、股权集中度（FHSR）、企业规模（SIZE）、资本密度（CD）、偿债能力（LEV）和盈利能力（ROA）作为匹配变量。表6 分别列出了2010 ～2017 年各年以及2010 ～2017年整体的分数对数模型的估计结果。

从分数对数模型回归的拟合优度AIC指标可以看出，该模型拟合效果很好。政府补助与R&D 投入显著正相关，这和多数学者的研究结论是一致的，即政府补助有利于企业获得外部专项资金以提高研发支出强度。高管激励与R&D 投入只在模型（1）和模型（3）中显著负相关，一方面说明高管持股水平过高，并不利于企业R&D 投入。苗淑娟等[29]、徐宁等[31]研究发现，高管激励与企业R&D投入呈现“倒U型”关系，本文前述分析发现中小板企业高管持股比例普遍过高，正是呈现出“倒U 型”的后半程关系。另一方面从单一年份看，高管激励与R&D 投入并没有显著关系。从长期看，这两者之间的相关关系是显著的，但是通过回归系数，可以看出两者之间的相关程度较弱。除了模型（2），股权集中度与R&D 投入显著负相关，说明对于中小板企业而言，股权集中会抑制企业研发投入，原因可能是研发是一项高风险、长周期的活动，中小企业控制性股东更倾向于尽快将企业发展壮大而非冒险投资，同样从回归系数来看，两者之间的相关程度也不大。除了模型（3）和模型（5），企业规模与R&D 投入显著负相关，说明企业规模越大，越倾向于规避风险，减少类似于研发创新等高风险活动的投入。资本密度与R&D 投入显著负相关，说明人均资本高的企业限制了企业的R&D投入。偿债能力与R&D投入显著负相关，说明企业负债水平越高，越不利于企业研发投入，高负债率企业风险较大，难以再进行高风险投资。值得注意的是，除了模型（2），其余回归结果均显示盈利能力与R&D 投入显著负相关，这是因为本文选取的R&D投入指标是R&D支出/营业收入，盈利能力指标是净利润/总资产。当营业收入越高时，企业的净利润也就越高，营业收入作为R&D 投入指标的分母，净利润作为盈利能力指标的分子，回归结果显示盈利能力与R&D投入显著负相关。

估计出R&D 投入的条件分布之后，便可计算GPS。基于表6的回归结果，计算各样本的GPS如表7所示。

（2）共同支撑假定检验。Heckman、Vytlacil[32]指出，非参数的匹配方法只有在共同支撑领域才是有效的，以保证处理组和对照组能够找到各自的匹配对象。共同支撑指在倾向得分匹配法中处理组和对照组要有足够的重叠区域。当处理变量是二元变量时，使用PSM方法可以把倾向得分位于尾端的个体删除，使得处理组和对照组中各自的最大值和最小值相等，以确保有足够的重叠领域。然而对于处理变量是连续变量的情形，处理变量不能像二元变量那样分为处理组和对照组。为了比较“无限数量”的处理变量和对应的GPS 得分，借鉴Flores 等[33]、Sheldon 等[17]的做法，本文将处理变量划分为两个区间作为两组，并将GPS得分也划分为区间，如图2所示。

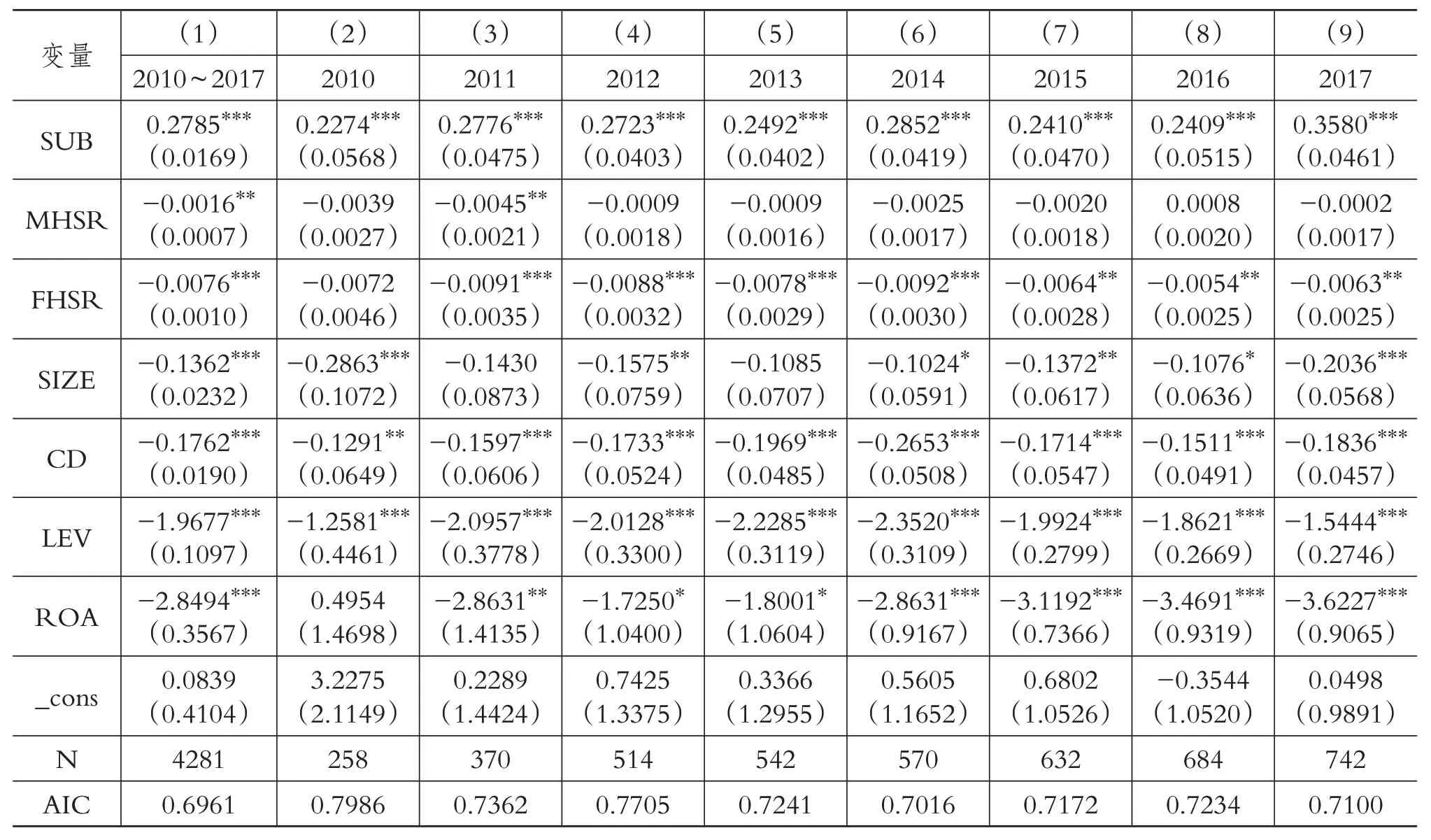
表6 R&D投入的条件分布——分数对数模型回归结果

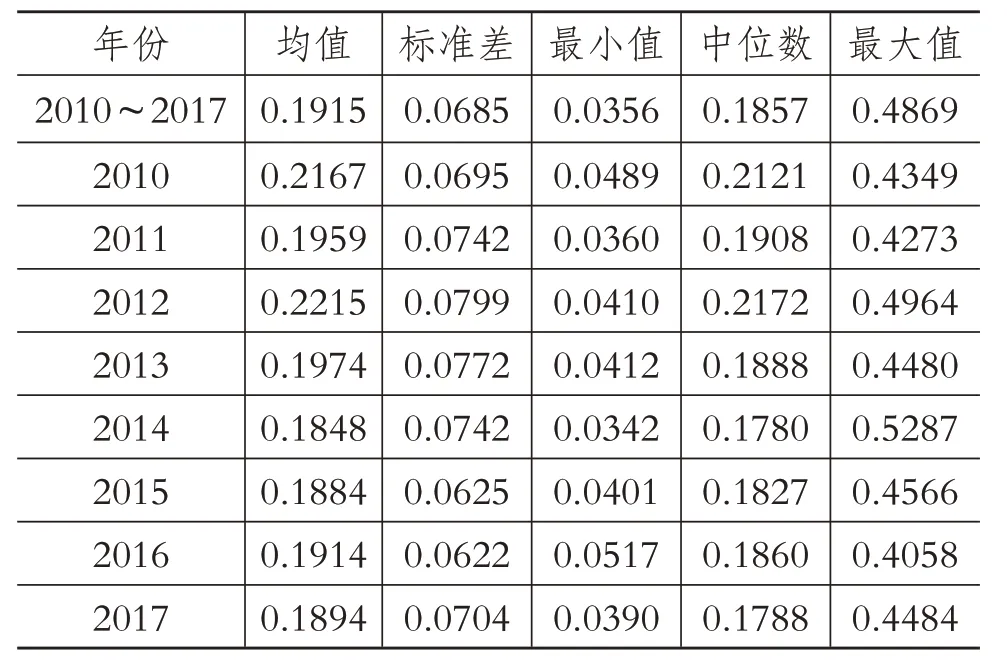
表7 GPS的描述性统计

根据图2 可以看出，不管是2010 ～2017 年的总样本，还是2010 ～2017 年各年的样本都有足够的共同支撑领域。因此在接下来的分析中可以确保在GPS得分相同的情况下，不同R&D投入强度的个体可以找到与之对应的匹配对象。

（3）平衡性质假定检验。倾向得分匹配法在满足平衡条件之后，才能更好地消除不同对象匹配变量之间的差异。因为处理变量是连续变量，本文借鉴Hirano、Imbens[15]的做法将处理变量 R&D 投入按照区间分成两组，检验两组样本在匹配后各个匹配变量的均值差异是否能够被削弱。由于版面的限制，表8只列示了2010 ～2017年总样本的平衡性质假定的检验。

可以看到，在GPS 调整之前，各个匹配变量均值都存在显著差异。经过GPS 调整之后绝大多数不再存在显著差异，只有高管激励、企业规模、偿债能力和盈利能力的第二组均值之间还存在显著差异。而这四个匹配变量均值差异都有了大幅度降低，并且显著性也有所下降。从各年的平衡性检验来看，在5%的显著性水平上，只有2012年、2014年和2017年个别匹配变量在经过GPS 调整之后均值还存在差异，但是均值差额的绝对值和显著性有了大幅度降低。对此，可以认为GPS较好地满足了平衡条件，即前文提到的第二个假定，因此可进行后续研究。根据GPS方法的第一个假定，即条件独立性假定，本文在给定GPS得分之后，R&D投入与企业创新绩效相互独立。

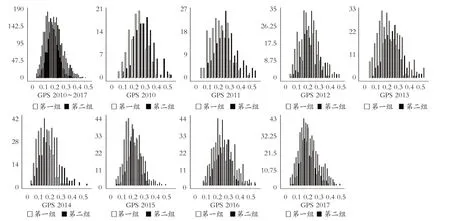
图2 GPS的分布

表8 2010～2017年GPS的平衡性检验

2.估计结果变量企业创新绩效的条件分布。根据计算的GPS 和RD，可以进一步估计企业绩效的条件分布。由于假定主效应（RD 和GPS）不能从估计结果变量的方程中剔除[34]，因此本文根据具体情况对企业绩效进行了估计，即优先保证RD 和GPS保留并显著，然后逐步加入二次项和交互项。当主效应都不显著，且加入二次项和交互项不会改善这一情形时则不再加入二次项和交互项，当主效应其中一个显著且加入二次项和交互项不会恶化这一情况时则视情况酌情加入二次项或交互项。具体回归结果如表9所示。

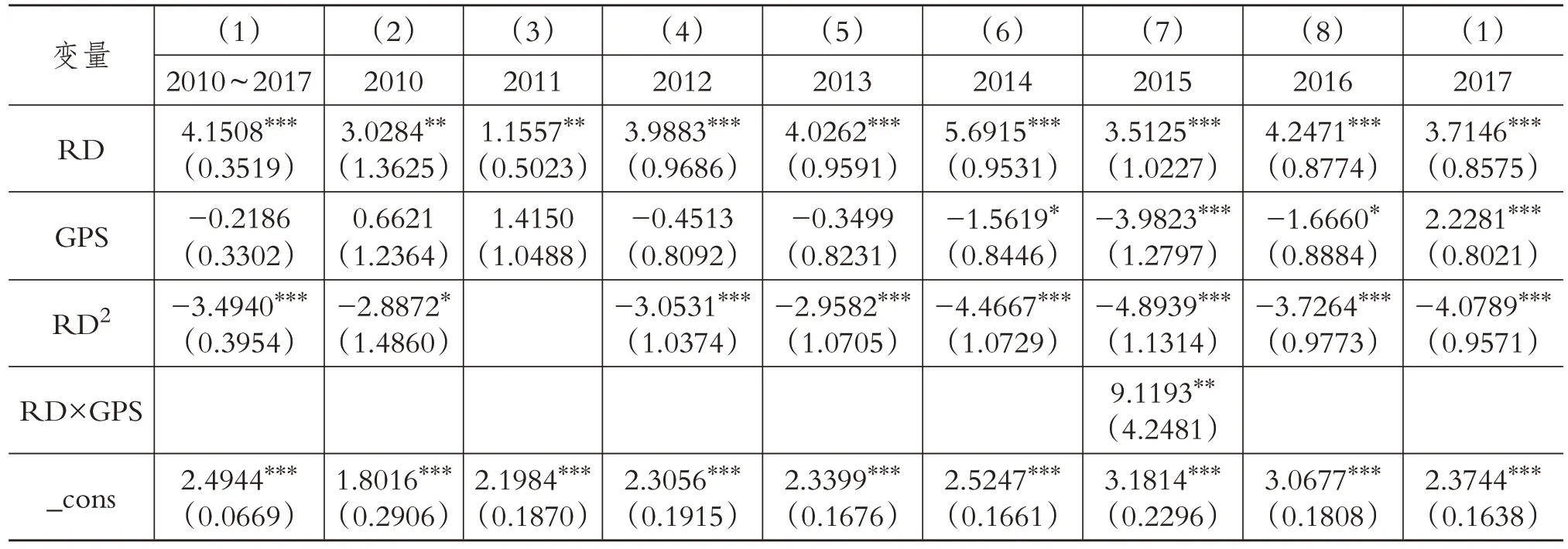
表9 企业创新绩效条件分布的估计结果

模型（1）是 2010 ～ 2017 年总体样本的回归结果，从各个系数的显著性来看，该模型能够较好地估计企业创新绩效的条件分布。从2010 ～2013 年各年份回归结果来看，GPS 均没有通过10%显著性水平上的t 检验。但是GPS 不显著只能说明经过调整后的匹配变量（或者称之为控制变量）对企业绩效的影响不显著，而且仅仅局限于2010 ～2013 年各年的样本，并不影响R&D 投入对企业创新绩效影响的分析。且导致这种结果的一个重要原因是2010 ～2013年各年的回归样本过少，而使用倾向得分匹配方法的一个重要前提就是具有一定数量的样本数以实现观测值之间的匹配。各个模型均显示R&D 投入显著不等于0，这与多数学者的结论一致。本文认为R&D投入对企业创新具有显著正向影响，但是除了模型（3），R&D 投入的二次项系数也同样显著不等于0，并且其系数都是负值，因此R&D 投入对企业创新绩效的影响更加符合“倒U型”趋势，这与描述性统计的结论是一致的。加入GPS 的二次项均会导致主效应不再显著，因此模型（1）～（9）不再加入GPS的二次项。同理，加入交互项后除了模型（7），其余模型的主效应也不再显著，因此除模型（7），其余模型不再加入交互项。

由于模型（3）样本量的限制，无法继续使用GPS方法研究2011年企业的样本。为研究“倒U型”关系在2011 年是否成立，使用最小二乘法检验R&D 投入的二次项是否显著，计算结果见表10。结果显示R&D 投入的二次项为负，且在5%的显著性水平上通过了t 检验，说明对于2011 年的样本，R&D 投入与创新绩效的“倒U型”关系依然成立。具体结果如表10所示。

表10 最小二乘法下R&D投入与企业创新绩效关系的回归结果

3.估计剂量反应函数和处理效应函数。

（1）剂量反应函数。将R&D 投入划分为多个子区间，然后在每个子区间估计出R&D 投入对企业创新绩效的因果效应，将这些因果效应用串联起来便是剂量反应函数。本文根据前述对企业创新绩效的估计，将R&D 投入在［0，1］的范围内划分成100个子区间，剂量反应函数如图3所示。

图3显示，2010 ～2017年间R&D投入与企业创新绩效呈“倒U 型”关系。即当企业的R&D 投入小于某一临界值时，随着R&D 投入的增加，企业的创新绩效也随之增加；但是当企业的R&D 投入大于这一临界值时，随着R&D 投入的增加，企业的创新绩效不增反降。因此R&D 投入并不是越多越好，这一结论也支撑了孙晓华、辛梦依[35]的观点。

对于R&D 投入与企业创新绩效呈“倒U型”关系的原因，可以解释为：在拐点之前，随着R&D 投入的增加，企业的知识储备会增加，对新知识的学习能力、吸收能力也会不断增加，这就会提高企业自身的知识水平和创新能力，从而促进创新绩效的提升。除此之外，随着R&D 投入的不断增加，企业中就会产生一种知识资本的规模效应，促使企业有能力引进更多先进的技术、人才和知识，不断实现创新，带来创新绩效的不断提升。企业的生产、销售等各个环节也会因为规模效应变得高度集成化，从而提高创新速度，增加企业创新产出[36]。但是R&D投入也是要素资本的一种，也会存在边际报酬递减的规律，当R&D 投入超过拐点之后，R&D 投入的边际成本就会大于边际收益，此时继续增加R&D 投入反而降低了企业的创新绩效。R&D投入的边际报酬递减已经在瑞典、日本和美国等工业化国家得到了证实[35]。另一种解释是，目前我国的创新体系还不健全，可能存在着系统性失灵，也就是说创新政策和创新激励体制没有很好地促进企业的研发投入转化为专利成果[37]。

图3 R&D投入与企业创新绩效的剂量反应函数

如图3显示，除2011年外所有年份的R&D投入与企业创新绩效同样呈“倒U型”关系。2011年显示二者呈正相关关系，对企业创新绩效分布进行估计时，R&D 投入的二次项并不显著，这主要是因样本量过少导致使用倾向得分匹配受到了一定的限制。2011 年所显示的结果也恰好是部分学者研究发现R&D 投入与企业创新绩效呈正相关关系的一个体现，这也说明实证研究中，最好选择面板数据，以尽可能避免估计结果的偶然性。

（2）处理效应函数。为研究企业进行R&D 投入相对于不进行R&D 投入对企业创新绩效的影响，图4给出了根据剂量反应函数后续得到的处理效应函数。

2010 ～2017年的处理效应显示，R&D投入与企业创新绩效呈现线性负相关关系。这表明对于一个企业而言，其R&D 投入强度的增加相对不进行R&D 投入而言，对创新绩效的净效应是逐渐递减的。如果把R&D 投入的取值划分成两部分（以图4中虚线与X轴的交点为界）可以发现：在交点之前，随着R&D 投入的增加，相对于不进行投入而言，企业进行R&D 投入更能提升企业的创新绩效。但是随着R&D 投入的增加，这种相对优势会有所下降，不过交点之前企业理性的做法还应该是增加R&D投入，交点之前的区域称之为有效区域；在交点之后，R&D 投入强度的增加相对于不进行R&D 投入而言，对企业创新绩效的效应是负的，增加R&D 投入变得不再理性，称之为无效区域。导致出现无效区域的原因可能是继续增加的R&D 投入已经超过了企业现时所需，甚至造成了企业资源的浪费。这时增加R&D 投入给企业带来的效益弥补不了企业资源的浪费，或者说此时R&D 投入的边际收益已经远远小于R&D投入和其他资源的边际成本。

图4 R&D投入与企业创新绩效的处理效应函数

图 4 显示，除了 2011 年，其余年份 R&D 投入与企业创新绩效的处理效应函数没有本质区别，2011年出现企业创新绩效的净效应不随R&D 投入变化的原因就是前文发现2011年R&D投入与企业创新绩效线性正相关。

表11 给出了进一步计算得到的剂量反应函数“倒U 型”关系的拐点区间和处理效应函数的无效区域点区间。

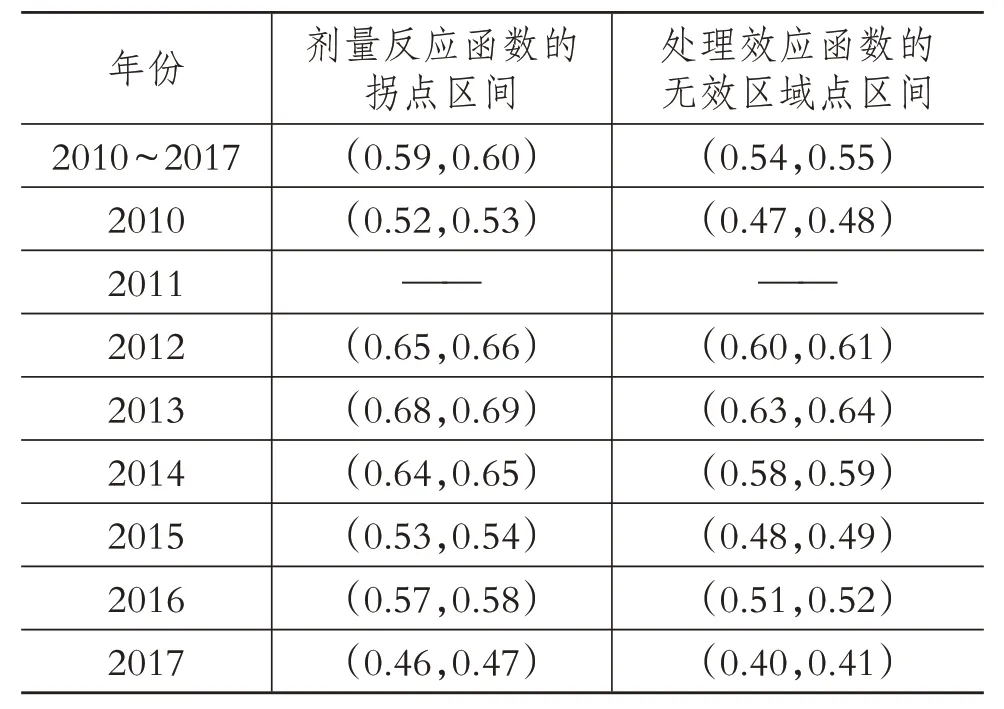
表11 剂量反应函数拐点和处理效应函数无效区域点的分析

表 11 显示，2010 ～ 2017 年整个样本和 2010 ～2017年各年份样本的无效区域点均在拐点右侧，这表明R&D 投入的强度在达到无效区域点之后的一小段区间还能继续增加企业的创新绩效。将剂量反应函数和处理效应函数结合起来，得到图5。OA 即是有效区域，在有效区域内，增加R&D 投入对企业创新绩效绝对有益。如图5（1）所示，在AB 阶段，企业增加R&D 投入可以进一步提升企业的创新绩效，但需要付出较大的代价，甚至会出现R&D 投入已超过企业现时所需的情况，造成资源的浪费。此时与其继续增加R&D 投入，不如通过其他手段提升企业创新绩效。为解决这个问题，一种方法是实现无效区域点的右移，20 世纪30 年代数学家Cobb 和经济学家Douglas提出来的Cobb-Douglas生产函数很好地诠释了这一点。企业可以通过提高技术来提升企业绩效，因此企业可以引进更高科技含量的设备，提升企业的生产效率，从而支撑起大强度的R&D投入，缩小AB之间的距离；另外还可以通过健全国家创新体系，完善法律制度，给予企业更多便利，不断提升企业的成果转化效率，最终实现剂量反应函数的拐点和处理效应函数的无效区域点重合，如图5（2）所示。

图5 剂量反应函数和处理效应函数

五、研究结论和建议

R&D 投入对企业创新绩效的影响一直是学术界和实务界关注的重要问题，但是相关研究还存在一定的局限性，本文借助GPS方法，利用2010 ～2017年中小板企业的数据，深入细致地探讨了R&D 投入对企业创新绩效的影响。

研究表明R&D 投入与企业创新绩效是一种“倒U 型”关系，且一个企业增加R&D 投入与不进行R&D 投入相比，获得的相对优势是逐渐下降的。随着R&D 投入的增加，可能会导致企业资源的浪费，陷入一种继续增加R&D 投入的无效区域。并且无效区域总是先于“倒U 型”的拐点出现，说明在“倒U 型”前半程的后期，继续增加R&D 投入固然能够提升企业创新绩效，但是这种提升会让企业付出很大的代价和多倍的努力。在使用2011年的企业数据时，由于数据量的限制，使用普通最小二乘法同样验证了R&D投入与企业创新绩效的“倒U型”关系依然成立。本文使用的GPS 方法的第一个假设是在给定匹配变量之后，处理变量与结果变量相互独立，但是没有观测到全部的潜在影响处理变量和结果变量的匹配变量。这也是本文需要后续深入研究之处。

基于以上研究结论，本文提出以下建议。第一，我国中小企业目前仍然存在R&D 投入不足的问题。对企业而言，要积极响应国家创新号召，加大R&D投入，大胆创新；同时还要注重R&D资源的优化配置，根据企业所处的不同阶段控制过度的R&D投入。企业应该根据自身情况，保证R&D 投入占营业收入的比例最高不超过50%～60%，在进行R&D投入或者引进相关技术设备时，应该优先考虑基础设施投入，提高生产效率，不能让无效区域过早出现。第二，对于政府而言，应该鼓励创新，加大投入扶持力度，给予企业更多的政策支持，以提高企业的成果转化效率。同时还要不断优化创新发展环境，加大对知识产权的保护，完善创新体系。