磁物质表面波的自旋
张娇娇 王 鑫
(首都师范大学物理系,北京 100048)
0 引 言
金属表面等离激元(surface plasmon polariton,SPP)是在金属表面由光场和金属相互作用形成的一种电磁波[1-2].它沿着金属表面传播并随着离开表面的距离而衰减.SPP的自旋并不像通常光子那样沿着传播方向,而是与传播方向垂直,这被称为反常自旋.更重要的是,自旋方向与传播方向的关系是固定的,被称为自旋-轨道锁定.巧妙利用这个性质可以导致光子自旋霍尔效应的产生[3],这为信息技术提供了一个新的物理基础,潜力巨大,引起了人们浓厚的兴趣[4-8].金属表面之所以能够产生SPP波,一个很重要的原因是金属的介电常数ε<0[9-10],而材料电磁性的差异主要由介电常数ε和磁导率μ共同决定,电磁材料也因此分为了双正材料,双负材料,电单负材料和磁单负材料.对于磁单负材料[11],理论上也可预知有类似于SPP那样的电磁波[12],不妨称为MSPP波.MSPP是横电波,这与SPP的横磁波是对应的,反映了电与磁的对称性.但是MSPP更容易与激发波达到波矢匹配,即更容易获得MSPP波[12-14],这样自然会想到一个有趣问题,MSPP的自旋是怎样的.
本文利用解析推导与模拟验证的方法对MSPP的自旋进行研究,得到了一些有价值的结果.
1 理论分析
光子自旋的垂直分量表示为[3]:
(1)
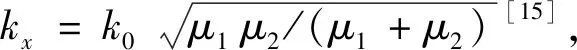
(2)
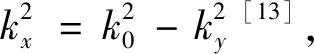
(3)
MSPP产生于磁单负材料表面,当磁单负材料的磁导率μ2<-1时,可知kx为实数,而ky为虚数,即ky=ik′y。将波矢带入公式(1)得:
(4)
由此可以看出MSPP的自旋的大小仅与磁介质的磁导率相关.
下面以实际的铁磁材料铁为例进行具体计算,其磁导率为[14]:
(5)
其中ω0=γH0,ωm=γM0[16],γ=2.210 174×105M/As为回磁比,M0=1.750×106A/m为饱和磁化强度,H0是外加磁场。将以上参数带入磁导率计算公式(5)可得:
(6)

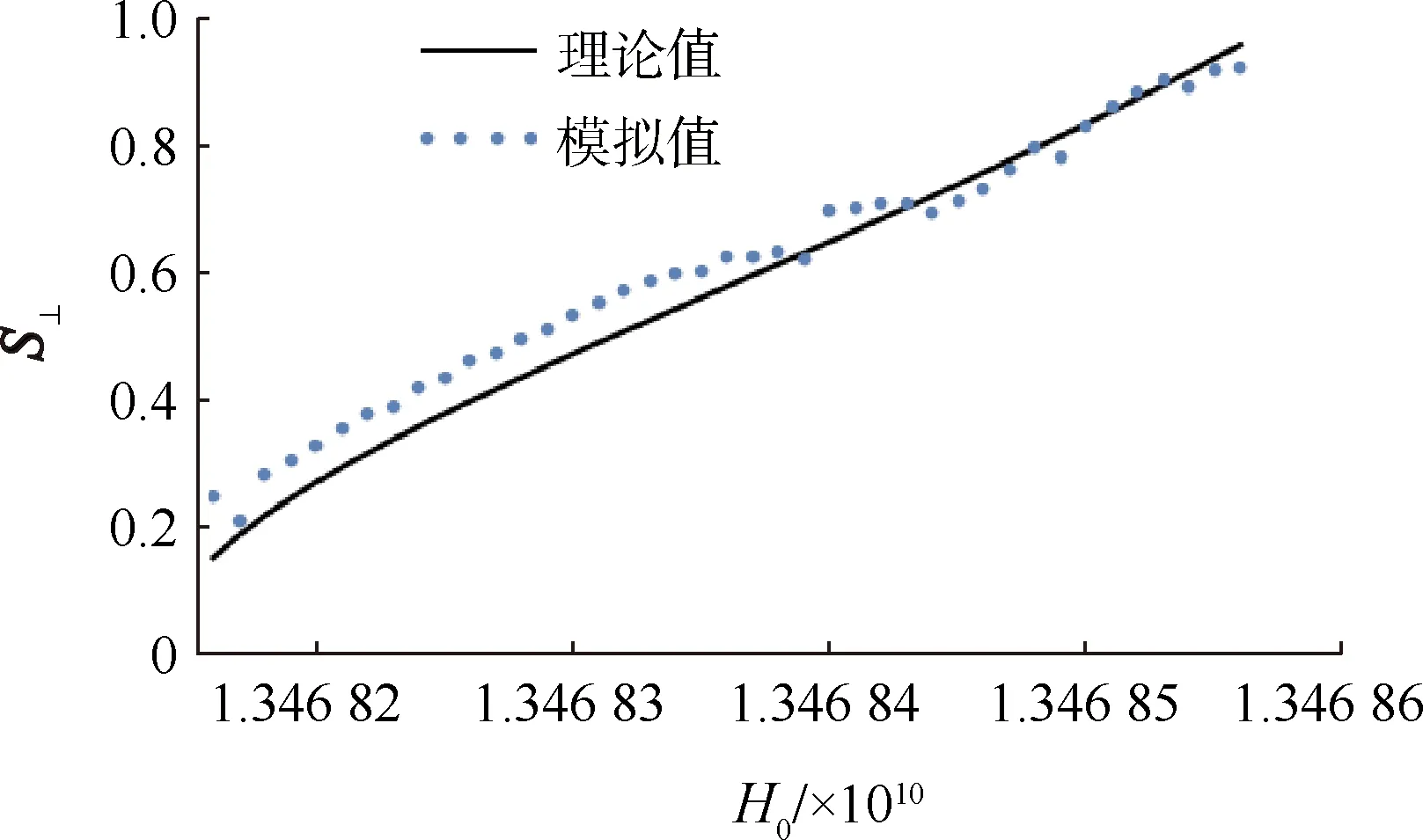
图1 MSPP的自旋垂直分量随外磁场的变化曲线图
MSPP自旋的方向沿着坐标系z轴或正或负,这与y方向的波矢有关,因此MSPP的自旋方向也与y方向的波矢相关,从而MSPP的自旋方向是与其传播方向是锁定的,这与电介质表面的SPP的自旋霍尔效应是类似的[3].根据电磁波的性质,对于y轴正方向的波矢,其自旋的方向如(7)式所示,由于磁导率μ2<0,所以,其自旋为z轴正方向,而对于y轴负方向的波矢而言,其自旋沿着z轴负方向,但是由于磁介质界面中的电磁波相对于真空界面的电磁波而言很小,因此本次研究以真空界面的电磁波为主,即y轴正方向的MSPP波.
(7)
2 模拟实验
为了验证理论,这里采用时域有限差分法(finite difference time domain,FDTD)对电磁波进行仿真和模拟.该方法基于麦克斯韦方程,投影到直角坐标系中,电场与磁场各节点的空间排布形成Yee元胞.在Yee元胞中,每一个电场分量由4个磁场分量环绕,每一个磁场分量由4个电场分量环绕.此外,电场与磁场在时间顺序上交替抽样,抽样时间间隔彼此相差半个时间步,使得麦克斯韦旋度方程在离散以后构成显示差分方程,从而可以在时间上迭代求解.因此,当建立模型后,给定了电磁场问题的初始值和边界条件,就可以得到场分布,而这正是本工作所需要的.
建立如图2所示的模型,两块磁性材料中间的缝隙是为了激发MSPP,入射光从下面向上入射,所有参数与前面理论计算时使用的相同.由于MSPP是TE波[12],可以对其磁场分量进行观测.图3是在狭缝右侧xoy平面上某小区域的磁场分布随时间的变化.从小图(a)到(r)共有18张,正好是一个周期的变化,每个小图时间间隔为1.251×10-16s.为了看的更清楚,不妨盯住图中心的矢量(第3排第3列).在(a)中这矢量是竖直向下的,经过1.251×10-16s, 变成了图(b),矢量逆时针转过了一个偏角.这样经过一周期,矢量最后逆时针旋转一周恢复原状(图(r)).因此磁场是随着时间逆时针旋转的,这对应着自旋沿着z轴正方向.而狭缝右侧的MSPP是沿着x正向传播的,这样就形成了轨道-表面-自旋三者的右手手征锁定关系,这与SPP是一致的.
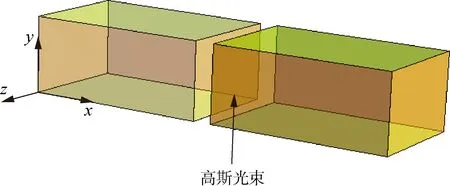
图2 三维模式下高斯光束激发MSPP波模型
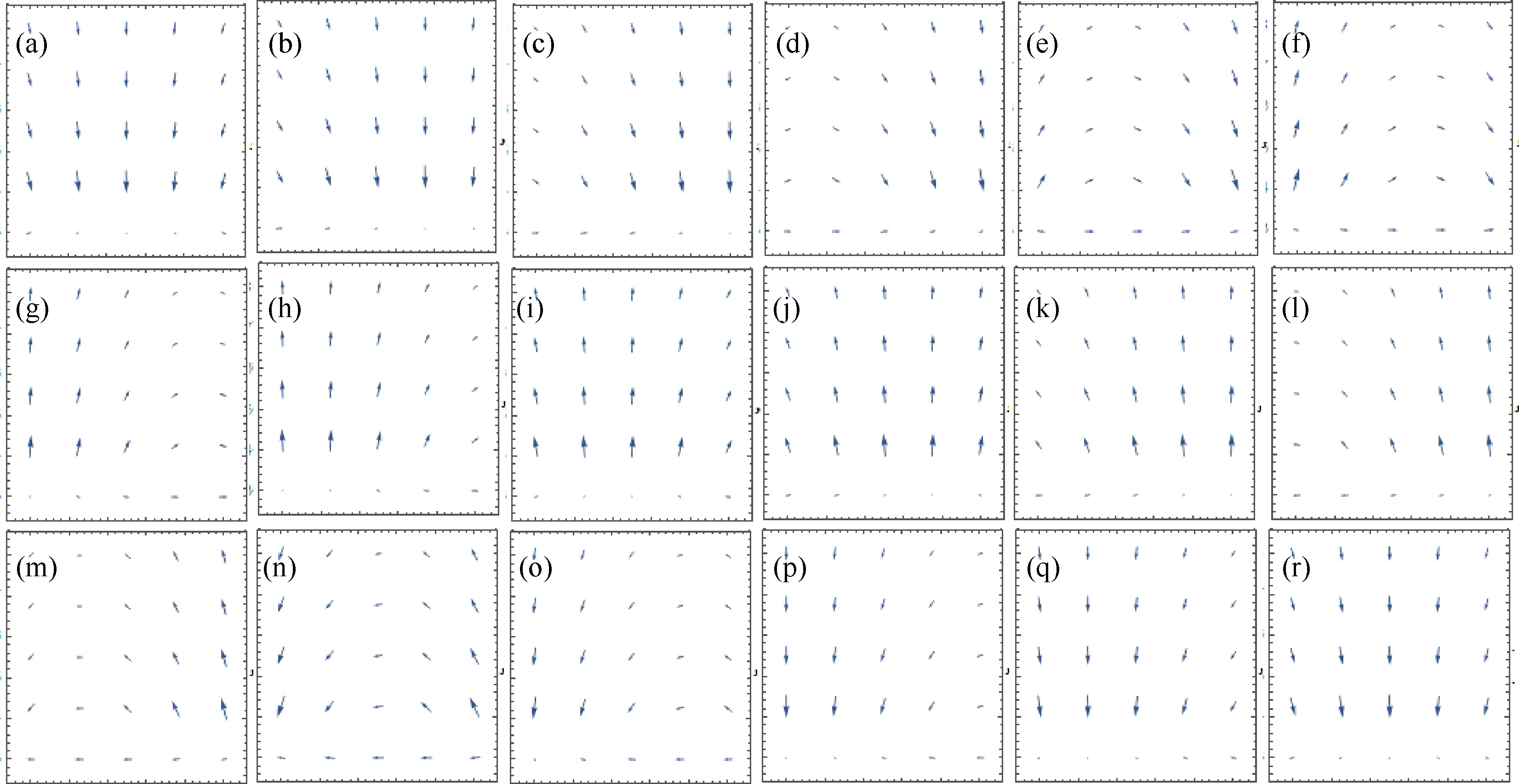
图3 狭缝右侧xoy平面的某小块区域电磁场分量随时间变化图
自旋的大小可以用间接的方法测得.由于电磁波的波长是相邻两波峰或两波谷之间的距离,因此可以在数值模拟中测得MSPP的波长λMSPP,而后根据kx=2π/λMSPP和k0=2π/632.8 nm可得k′y,从而根据S⊥=k′y/kx得到MSPP的自旋大小。结果用点表示在图1中,它的变化规律与理论计算结果吻合。说明本文中关于MSPP的理论预言是正确的。
最后本文给出电磁场各分量的模拟结果,如图4所示.在图1的坐标系下观察xoy平面的电磁场,可以发现电磁场分量Ex,Ey和Hz都为0,而Ez,Hx和Hy都不为0,因此该磁性材料表面的电磁波即为TE波.
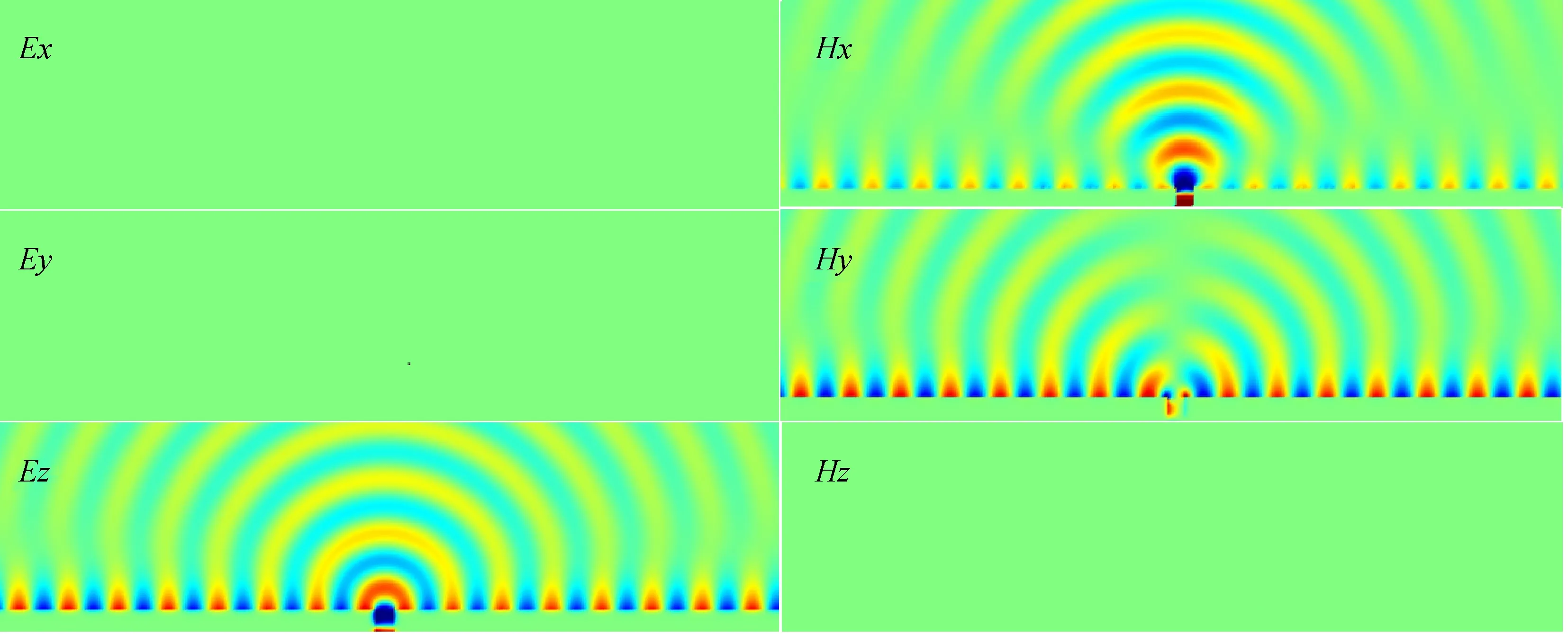
图4 电磁场各分量的模拟结果
3 结 论
本文用解析理论计算铁磁材料的MSPP波,证明了MSPP波的自旋反常及自旋-轨道锁定特性,并且得到数值模拟的验证.外加磁场还可以调控反常自旋,且二者为近似线性关系.这为实际应用提供了一条新路.

