两种不同井网稠油的渗流压力场分布

焦 焕，代玉杰，王学慧，鞠启明

（1.辽宁石油化工大学理学院，辽宁抚顺 113001；2.辽宁石油化工大学石油天然气工程学院，辽宁抚顺 113001）

稠油富含胶质和沥青质，胶质和沥青质属于高分子化合物，具有极性大、表面活性强的特点，因此稠油在储层中流动时，会有明显的固-液界面之间相互作用，这种作用使稠油的流动性变差[1]，渗流阻力增大[2]，增加了稠油的有效开发难度，导致生产效率降低，开发成本增高[3]。

稠油开采包括两个主要过程，即外界对稠油的加热和稠油在储层中的渗流。稠油在被加热的同时，还会在地层和外界的压力作用下流向生产井，这就是稠油的渗流过程。稠油的渗流是稠油开采中非常重要的环节，全面认识稠油的流变性质，精确定量描述稠油的渗流机理和特征，对提高稠油的采收率及稠油油藏开发方案的编制与实施具有重要意义。

稠油渗流是一个非常复杂的过程，此过程由储层性质、稠油的自身特性和流动状况等因素共同决定。目前对稠油渗流规律的研究主要包括室内实验和数值模拟两种方法。室内实验方面，Zhao 等应用三轴渗流装置模拟裂缝渗流，给出了岩石裂隙渗流和孔隙压力的本构方程[4]。李晓平等研究了河南油田的稠油，得出储层温度和原油黏度之间的关系[5]。Xu 等利用物理化学渗流仪，模拟了不同温度时的岩石裂隙的稠油渗流，给出了压差和温度的二元定量方程[6]。刘冬青等利用蒸汽驱物理模拟装置，得出了稠油温度和相对渗透率的关系[7]。张代燕等利用高温相对渗透率实验装置，模拟了稠油在储层中的渗流情况，但对稠油渗流机理未做深入研究[8]。实验方法得到的结果接近实际情况，但实验存在局限性，并且成本较高，在某些方面制约了自身的发展。

数值模拟方法具有成本低、计算周期短等优势，弥补了实验方法的不足。常用的求解稠油渗流规律的数值方法主要有差分法、有限元法和边界元法等[9]。例如，Sun 等用有限元方法分析了轴对称瞬态渗流问题，该方法只需对截面进行有限元网格划分，每个时间步长的自由曲面无需迭代，即可计算得到结果，大大减少了计算量[10]。但当油藏状况比较复杂时，不规则的油田边界形状和边界压力变化会给数值计算带来较大的困难和明显的误差，传统的数值模拟方法在处理这类问题时存在一定的困难，有限差分法和有限元法对求解问题的适应性变差，此时边界元方法求解复杂边界形状和边界条件渗流问题的优势便显现出来了。

边界元法是求解偏微分方程的一种数值方法，求解时，首先应用格林公式将待求解区域内的微分方程转换为边界积分方程，这一过程被称为问题的边界化。边界化过程完成后，即可对边界进行剖分，将边界分割为有限的边界单元，当给定具体的边界条件和初始条件后，即可进行数值模拟。离散过程中，剖分只在边界上进行，因此计算误差只来源于边界，区域内部是用格林公式精确计算的，因此，与传统的数值方法相比，边界元方法具有更高的计算精度[11]，受到学者们的青睐，成为数值模拟油藏渗流规律方法的首选。同时，边界元方法对无限大区域问题和任意边界形状问题均有较好的适应性[12，13]，对油藏中存在不渗透区域的渗流问题，也能很好地解决[14]。鉴于边界元方法的上述优势，本文拟采用边界元方法，对稠油渗流压力场进行数值研究。

1 边界元方法简介

边界元方法是继有限差分法和有限元法之后，近年发展起来的一种新的计算方法，其数学基础是积分方程理论，此方法是工程数值分析的有效工具。边界元处理一个具体的工程问题有两个关键步骤，第一步是将区域的定解问题转化为只考虑边界条件的问题，即问题的边界化，这一步可以使待求解的问题降低一个维度，因此计算的精度和效率都优于其他数值方法。另一步是边界的离散化，其主要目的是将边界积分方程离散为代数方程，然后对求解的问题进行数值模拟。

研究渗流问题的主要任务是求解Darcy 方程[15-17]，Darcy 方程的矢量形式可写为[18]：

式（1）中V 和K 分别表示达西流速和渗透系数，其标量形式分别为vx、vy、vz和kx、ky、kz。u 是势函数，在本文中，势函数表示压力。结合连续性方程和控制方程，对（1）式进行推导，可得二维渗流的定解问题。

式（2）中的Q 表示区域Ω 内的源或汇，Г1和Г2表示部分边界，是边界Г1和Г2上的已知量。用加权残量法对方程（2）进行推导，可得边界积分方程，详细推导过程参见文献[19]：

得到方程（3）所示的边界积分方程以后，问题的边界化就完成了，下一步就是对边界进行离散处理。

本文采用常单元，对边界积分方程进行离散，离散时边界曲线用直线段近似代替，将区域Ω 剖分为m 个单元Ω1，Ω2，…，Ωm，将边界剖分为（n-m）个边界单元Гm+1，Гm+2，…，Гn。由此，边界积分方程的离散化形式可写为：

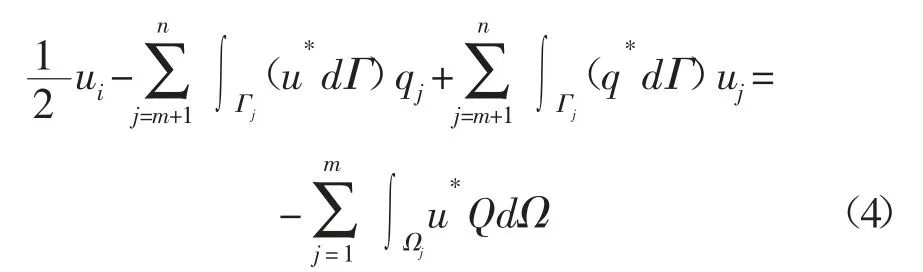
为了表述方便，本文引入含有n 个未知量的向量X，则式（4）可化简为：

式（5）中的系数矩阵A 和向量F 都是已知的或可求解的，通过求解方程（5），即可求得所有的未知量。对边界积分方程进行离散之后，即可用FORTRAN 语言编写程序，求解稠油渗流场的压力分布。由于篇幅限制，推导和离散过程详见参考文献[19]，本文不再赘述。

2 物理模型和数值模拟结果

在本文的数值模拟过程中，式（1）中达西方程的渗透系数由方程（6）给出[20]，本文考虑各向同性二维渗流问题，渗透系数满足kx=ky=k。

式中：b 是裂缝宽度，即两壁面之间的法向相对距离，且此裂缝被颗粒直径为d 的细小颗粒填充，稠油储层由无数条裂缝构成。g 是重力加速度，n 是孔隙率，μ是黏度[21]：

其中：API 为油品的重度，本文取API=20，T 是稠油温度，fw是稠油含水率，f1为稠油胶质及沥青含量，q为油品重度和温度的函数且满足q=2.169 24-0.025 25×API-0.688 75lgT。

为了使模型更接近工程生产，本文考虑了九点布井和二十五点布井两种模型。九点法布井的示意图（见图1），在无量纲边长为10 的正方形油藏区域内，共有九口井，其中一口注入井位于正方形油藏的中心，其余八口生产井对称分布于注入井的周围。

用边界元方法求解稠油渗流压力场分布时，需要对内边界（注入井和生产井的边界）和外边界（油藏边界）进行离散，图1 中的实心圆点表示内边界和外边界的离散点，数值模拟时，每一个离散点对应一个计算节点。一般来说，一些边界上的值是以边界条件的形式给定的，另外一些边界值则是计算得到的，求出边界上的值后，即可将边界上的值作为已知量，进一步求解油田内部的渗流压力场分布。

图1 九点布井示意图

图2 九点布井渗流场三维压力分布图

在稠油生产过程中，经常在注入井中注入高温高压蒸汽，以期达到增加地层压力，降低稠油黏度，提高稠油流动性和采收率的目的。注入井无量纲压力为1，油藏边界无量纲压力为0.8，八口生产井边界的无量纲压力均为0.5 时，稠油渗流压力分布图（见图2）。由图2 可知，最大压力位于油藏中心，且最大压力值为1，油藏边界压力和生产井边界压力均与给定的边界条件相符。八口生产井周围的压力分布具有良好的对称性，这种对称性是由井位分布的对称性和给定边界条件的对称性决定的。压力场的对称分布反映了程序代码的正确性。由于注入井的压力大于生产井的压力，因此从注入井到生产井的渗流压力场分布呈现递减趋势；油藏边界的压力也大于生产井的压力，从油藏边界到生产井的渗流压力场分布也呈现递减趋势，此压力变化趋势与文献[22]中的结果吻合，渗流压力场变化的趋势验证了物理模型的正确性。

图2 中给出的三维压力虽然比较直观，但一些压力数据不能完全显示。为了更全面、清晰地显示压力分布，九点布井时，稠油渗流场的二维无量纲压力等值线分布（见图3）。图3 清晰显示，压力的最大值位于坐标（5，5）的位置，即油田的中心，这是因为在计算时，注入井的边界条件给定为1，从注入井到生产井，稠油渗流压力值逐渐减小；另外，由于生产井的边界压力为0.5，给定的油田边界压力为0.8，由生产井向外边界的压力逐渐增大，这一变化规律与给定的边界条件相符，也符合渗流的规律。图3 中稠油渗流的压力变化规律与文献[23]中的规律一致。

数值模拟时，图2 和图3 给定的边界压力条件是对称的，因此压力图也完全对称，这是一种理想化的模型。在稠油的实际矿场生产中，生产井边界压力和油田边界压力经常发生变化，为了使数值模拟结果更接近实际生产过程，假设坐标为（7，5）的生产井边界压力由0.5 变为0.2，注入井和其余七口生产井的边界压力不变。坐标为（7，5）的生产井边界压力变化前和变化后，稠油渗流压力等值线变化情况，实线和虚线分别对应于边界压力等于0.5 和0.2 的情形（见图4）。由图4 可知，左侧的实线和虚线是重合的，这是因为左侧给定的边界压力条件未发生变化；图形右侧的实线和虚线明显分开，由此可见，虽然只是坐标为（7，5）的一口生产井的边界压力发生很小的变化，但由于多口井的压力耦合效应，整个油藏的渗流压力场分布发生了明显的变化，这说明稠油渗流场的压力分布对边界压力条件非常敏感。

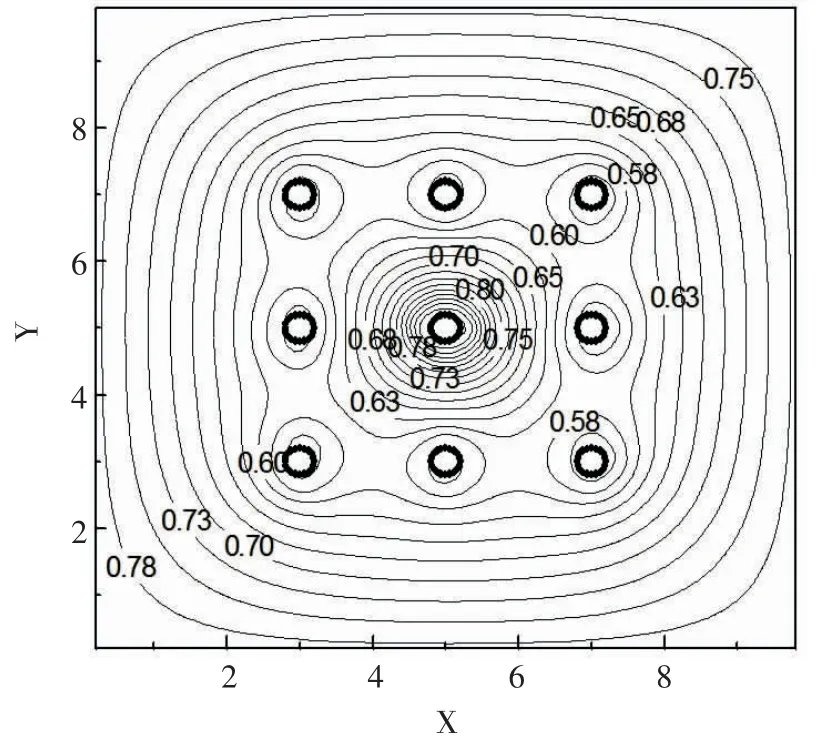
图3 九点布井对称压力等值线

图4 不同边界压力九点布井压力等值线

图5 稠油黏温关系曲线

图6 稠油渗透系数与温度关系曲线

温度是影响稠油黏度的重要因素，地层温度升高，会使稠油的黏度降低，渗透系数增加，使稠油更易于渗入生产井中。当稠油中胶质和沥青含量为50 %，含水量为2 %时，应用公式（7）计算得到的稠油黏度与温度之间的定量关系（见图5）。当温度小于70 ℃时，稠油黏度随温度的变化率较大；当温度升高到一定程度时，稠油黏度对温度的变化不敏感。将公式（7）求出的稠油黏度代入到公式（6）中，即可求出对应的渗透系数。裂缝宽度为0.1 cm，孔隙率为0.43，颗粒直径为0.053 cm时，稠油渗透系数与温度的关系曲线（见图6）。当温度小于70 ℃时，渗透系数与温度的关系曲线斜率有一定的变化；但当温度高于70 ℃时，曲线斜率的变化越来越小。这一结论与图5 的黏温曲线是对应的。

图5 和图6 的关系曲线表明，温度小于70 ℃时，稠油黏度和渗透系数受温度的影响比较明显，为了定量说明温度对稠油渗流场的影响，10 ℃（实线）和70 ℃（虚线）时，稠油的渗流压力场分布（见图7）。以无量纲压力0.78 所在的压力等值线为例，可以清晰看出，实线和虚线在空间上有了一定的距离，这是因为温度升高，导致稠油黏度降低和渗透系数增大，进而使稠油在储层中渗流时受到的阻力减小，能耗降低。

在矿场生产过程中，一个区块有几十口注采井，有时甚至达到数百口，为了使模型更具有一般性，本文给出了二十五点布井的物理模型（见图8），此井网共有二十五口注采井，其中九口井是注入井，其坐标分别为（1，1），（5，1），（9，1），（1，5），（5，5），（9，5），（1，9），（5，9），（9，9），其余十六口井是生产井。图9（a）给出了当所有注入井、生产井和油藏外边界的无量纲压力分别为1、0.5 和0.8 时，与图8 对应的稠油渗流压力等值线。由于注采井的分布和边界条件均具有良好的对称性，所以稠油渗流压力分布也是对称的，从注入井到生产井，压力值逐渐减小；从生产井到油藏边界，压力逐渐增大。这一规律与九点布井的规律类似，不同的是，由于此时注入井和生产井的井数增多，各井之间的压力耦合效应更加明显，稠油渗流场的压力分布更加复杂。图9（a）中的压力数据不够连续和直观，部分压力场的数据不能完全显示，图9（b）通过图形颜色的变化，对稠油渗流场的压力变化给出了全面直观的展示。

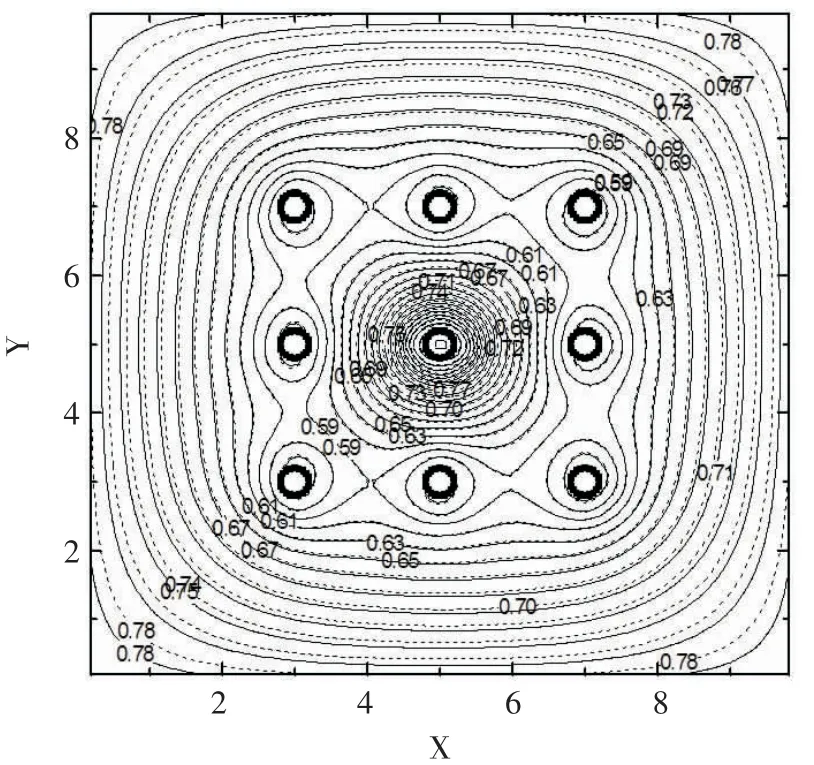
图7 不同温度稠油渗流压力等值线

图8 二十五点布井示意图

图9

为了进一步模拟边界压力条件对稠油渗流压力和注采井之间压力耦合效应的影响，将图9（b）中坐标为（1，7）和（3，5）的生产井的边界压力设定为1，其余注采井和油藏的边界压力条件均不变，从图10 的压力场分布明显看出，压力边界条件的变化对稠油压力场的分布有非常显著的影响。通过比较图4 和图10 可以看出，当边界压力条件发生变化时，二十五点井网渗流场的变化更明显，也就是说，注采井的密度越高，稠油渗流场的压力分布对边界条件的变化越敏感。

图10 二十五点布井非对称压力等值线

本文数值模拟过程中，为了考核程序的正确性，便于分析数值模拟结果，井网和边界压力条件的选择趋于理想化，但这并不影响边界元方法求解复杂边界多连通域稠油渗流问题的普遍适用性，这一普遍适用性已在文献[19]中有详细的论述，本文不再赘述。

3 结论

本文应用边界元方法（BEM），以储层介质和稠油油藏单元作为研究对象，首先建立多连通域低渗透油藏渗流的物理模型和数学模型，再将渗流力学基本理论和边界元方法结合起来，对求解的问题进行边界化和离散化处理，然后编写求解稠油渗流的通用FORTRAN 计算代码，应用此代码求解变系数达西方程，对九点布井和二十五点布井的稠油渗流压力场进行数值模拟，对不同边界压力条件时的稠油渗流场进行研究，分析了注采井之间的压力耦合效应，得到了如下结论：

（1）压力边界条件对稠油油藏的渗流场压力分布有明显的影响，在施工工程中，可以根据这一结论，通过压力分布情况判断储层的渗透情况。

（2）注入井与生产井之间的压力耦合效应与注采井的密度相关，注采井密度越高，耦合效应越明显。渗流场压力分布可为井位部署提供依据。

（3）当地层温度升高时（由10 ℃升至70 ℃），稠油黏度降低，渗透系数增大，稠油在储层中渗流时受到的阻力减小，能耗降低，此时的渗流压力场发生了明显的变化。

（4）数值模拟稠油渗流压力场时，虽然分析的区域很大，但用边界元法计算只需几秒钟，并且计算精度很高，这表明边界元方法处理稠油渗流问题的有效性和简捷性。