基于奇异值分解的简化数据应用
陈卉妍 张仁龙
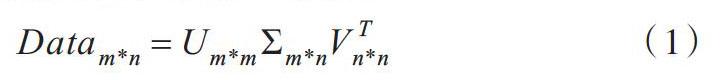

摘 要:奇异值分解是提取数据特征信息的一种强大工具,其应用可以从信息检索领域扩展到金融、医疗、统计学等各领域,是简化数据、相似度计算的一种有效方法。对奇异值分解原理和特性进行阐述,介绍了基于Python与其相关科学计算库的奇异值分解过程和相似度算法,解释了将庞大的数据矩阵映射到低维空间的转换过程,图像数据通过奇异值分解较原始图像压缩了近8倍。分别对SVD在推荐系统和图像压缩两方面的具体应用进行描述,总结出奇异值分解在数据降维中的强大应用和良好前景。
关键词:奇异值分解;推荐引擎;压缩图像;相似度計算;数据降维
DOI:10. 11907/rjdk. 191802 开放科学(资源服务)标识码(OSID):
中图分类号:TP392文献标识码:A 文章编号:1672-7800(2019)008-0162-04
Simplified Data Application Based on Singular Value Decomposition
CHEN Hui-yan, ZHANG Ren-long
(College of Computer and Information Engineering, Beijing University of Agriculture, Beijing 102206, China)
Abstract: Singular value decomposition is a powerful tool to extract data feature information. Its application can be extended from information retrieval to finance, medical, statistics and other fields. It is an effective method to simplify data and similarity calculation. The principle and characteristics of singular value decomposition are expounded in this paper. The process and similarity algorithm of singular value decomposition based on Python and its related scientific computing library are introduced. The mapping of huge data matrix to low-dimensional space is explained. The image data is nearly 8 times compressed by the singular value decomposition than the original image. The specific applications of SVD in recommendation system and image compression are described respectively, and the powerful application and broad prospects of singular value decomposition in data dimension reduction are summarized.
Key Words:Singular value decomposition; recommendation engine; compressed image; similarity calculation; data dimensionality reduction
作者简介:陈卉妍(1996-),女,北京农学院计算机与信息工程学院硕士研究生,研究方向为数据分析; 张仁龙(1967-),男,北京农学院计算机与信息工程学院教授、硕士生导师,研究方向为程序设计。
0 引言
信息时代,如何从海量数据中检索出具有价值的信息尤为重要。由于矩阵分解可应用于很多实际问题中,因而在诸多领域得到了广泛应用,例如推荐系统、信号处理、PCA降维、压缩数据去噪[1]等。在亚马逊的推荐算法中,将用户购买偏好与其他用户进行对比,据此预测该用户最可能感兴趣[2]的物品并推送给他。中国的淘宝、京东商城、当当书城以及苏宁易购都属于协同过滤推荐系统[3]在电子商务中较为成熟的应用典范。
奇异值分解就是矩阵的一种分解方法,利用这种规则的分解方式可用小而多的矩阵集表示原始数据集。而分解数据集的原理就是去除数据中的噪声和冗余信息,将矩阵拆分成一些小矩阵的点乘,这些小的矩阵就是被保留抽取出来原始数据的相关特征信息。这种分解的核心思想在于其对矩阵的波动并不敏感,因而可以在不改变矩阵相关度量的前提下,得出矩阵的秩,并且逐渐逼近该矩阵的最佳秩,从而使得数据被压缩[4]、简化。同样,该重要性质也可用于协同过滤[5]的推荐引擎中,将当前用户和其他用户的数据矩阵进行比较[6],使用最邻近方法向用户实现产品推荐。
1 奇异值分解原理
奇异值分解是一个能适用于任意矩阵的分解方法,对于一个任意m*n的矩阵都有如下分解:
[Datam*n=Um*mΣm*nVTn*n] (1)
Σ对角线上的元素对应原始数据Data中的奇异值[7],也即Data*DataT特征值的平方根。通常情况下,前1%~10%的奇异值就可以达到全部奇异值的90%[8]以上,因此可以利用前k个奇异值近似描述整个矩阵。将原始的m行n列数据矩阵分解成为m行k列的矩阵U、k行k列的矩阵Σ和k行n列的矩阵 VT。k是远远小于m和n的数,当k与n越相似时,3个矩阵相乘的结果越接近于原始数据Data。
[Datam*n≈Um*kΣk*kVTk*n] (2)
在Python的科学计算库NumPy中有一个很好的线性代数工具箱linalg,可以方便地实现SVD的具体分解。数据存储以科学计数法的形式展现,当数值过小时可以忽略不计以0代替。当Σ的对角元素中出现0时,为了节省存储空间,NumPy会自动将为0的元素删除,以提高运算效率。矩阵的存储面积越小,存储量就会远远小于原始数据矩阵Data,并且会在很大程度上提高相似度。分解后具体所需数据如图1所示。
图1 深灰色为计算需要数据
2 推荐引擎
2.1 应用原理
在传统推荐算法中,通常根据产品和用户数据构成的系数矩阵进行不同项目之间的相似度计算[9],以完成相似物品推荐。但真实存在的数据往往都是稀疏矩阵,会存在大量空值,使得计算机在运算中做了很多无用功。奇异值分解可以解决这类问题,将原始数据映射到低维空间[10]中,通过减少特征空间从而提高推荐效果,不仅克服了矩阵的稀疏性[11],还在最大程度上还原了原始数据矩阵。
推荐系统的基本思路是:首先加载原始数据集,定义计算相似度的方法,通过计算奇异值的百分比确定缩小的维度,再对降维数据中为空值的数据进行数值预测,最后以降序排列方式将评分最高的产品返回给用户完成产品推荐。
2.2 基于SVD的推荐引擎
在推荐系统中,使用最为普遍的一种推荐方法就是协同过滤[12]。首先对数据矩阵进行横向分析,利用奇异值分解找到与目标用户具有相似喜好的用户,再以矩阵的列为标准对比产品与产品之间的相似度,对用户没有评分的产品进行推荐,并给出相应的预测分值,以完成产品推荐。
在现有数据中,可以使用不同的距离计算方法计算产品之间的相似度。利用皮尔逊相关系数计算距离时,由于其对用户的评分量级并不敏感,因此这种算法会认为一个用户对所有产品都评价极高和一个用户对所有产品都评价极低是两个相等的向量。在Numpy中利用0.5+0.5*corrcoef()进行计算,最后规整其值在0~1之间。使用欧氏距离公式计算产品与产品之间的相似度时,先根据公式得出距离再利用“1/(1+距离)”计算相似度,就可以得到规整的在0和1之间变换的数据,当距离为0时相似度就越大越趋近于1,当距离越远相似度也就越趋近于0,以此简化运算过程。
[dx,y=(x1-y1)2+(x2-y2)2+?+(xn-yn)2] (3)
根据余弦相似度[13]计算产品之间的相似性时,如果两个向量夹角为90°则相似度为0,如果两个向量方向相同则相似度为1,可以利用Numpy线性代数工具所提供的linalg.norm()函数计算。
[similarity=cos(θ)A?B∥A∥∥B∥=i=1nAi×Bii=1n(Ai)2×i=1n(Bi)2] (4)
按照前k个奇异值的平方和占总奇异值平方和的百分比确定k的值,将原始的11维矩阵转换为3维矩阵。利用相似度计算方法,实现根据产品相似度对用户未进行评分的产品进行分值预测。对编号为1的用户推荐评分较高的3件商品,降序排列得出的产品序号和相似度结果如图2所示。
图2 产品推荐及评分预测
可以使用交叉检测方法对现有推荐引擎进行评价,将已知的原有数据删除,对其作出新的预测,查看原有数据与预测数据之间的差异并对推荐系统进行评价。通常利用最小均方根误差作为评价标准,通过取得均方误差的平方根进行具体数值评价。
3 图像压缩
3.1 应用原理
图像压缩的意义是在保证图像质量的前提下,利用更少的存储空间保存更接近于原始图像的图像。这样不仅可以压缩图像大小,减少存储位数,还可以加快图像数据传输速度,为人们的工作带来很大便捷。图像压缩[14]的原理是,存儲的数据之间存在着大量的重复和冗余[15],奇异值分解可以最大程度地保留原始数据并且去除重复数据[16],以压缩图像大小,同时保证图像质量。
3.2 基于SVD的手写数字压缩
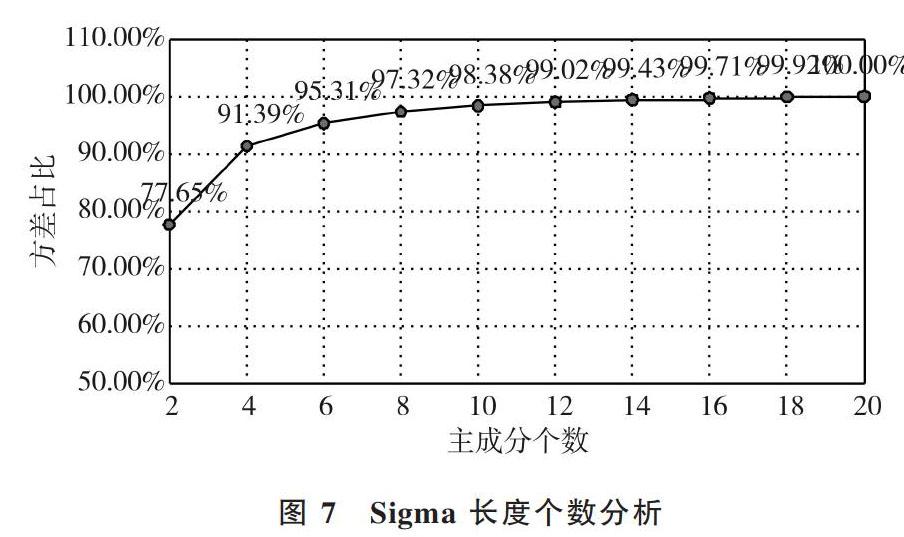
现有32*32的手写数字6图像一张,利用函数遍历其所有矩阵元素,在当前值大于阈值时打印1否则打印0,就可将原图片转换为0、1分布的共1 024像素大小的手写数字灰度图像。利用科学计算库NumPy中的linalg将矩阵分解为k位数的U、Σ和VT,其中Σ就是将k位数的奇异值Sigma填充到全0矩阵的对角线上,U为32*k的矩阵,VT为k*32[17]的矩阵。最后利用SigRecon实现3个矩阵的点乘重组[18],最大限度地还原了压缩前的矩阵图像。原始图像与取不同Sigma值时图像变化如图3-图6所示,Sigma长度个数分析如图7所示。
图3 原始图像 图4 Sigma=3压缩后图像
图5 Sigma=5压缩后图像 图6 Sigma=10压缩后图像
从数据中可以看出,随着Sigma值的不断增加,压缩后图像的还原度也越来越高。一般只要保留矩阵80%~90%的能量,就能够获得到主要特征并去除无用噪声。由此可以看出,只要有两个奇异值就可以实现以上图像的压缩重组。重组后的数据由U和VT两个均为32*2的矩阵组成,总数目是32*2+32*2+2=130个,相比原来的1 024个数字缩小了近8倍。以此类推,假设在n*n个像素的图像中,奇异值按照从小到大的递增顺序排序,选择k个奇异值逐渐靠近原始图像,就可以用 k(2n+1)个像素的数值替换原有n*n个像素的图像。压缩比为p=n2/k(2n+1),当k满足k 图7 Sigma长度个数分析 4 結语 奇异值分解在图像压缩中可以减少图像的内存空间,经过SVD分解后的图像比原始图像压缩了近8倍,同时也可以加快图像传输速度,有效提高图像传输效率。其在推荐系统中也起到了很大推动作用,可缩小原有矩阵维度,去除冗余提升运算效率。但是,推荐系统还需要考虑是选取基于产品[19]还是基于用户[20]的相似度计算比较适合,如果用户数目较多,可以选择基于产品的相似度计算,有利于减少工作量,这些具体实现方法需根据实际情况进行更改完善。此外,推荐引擎设计还需注意冷启动问题[21],可以将开始的推荐问题转换为搜索问题[22]。例如将不同的产品赋予不同的标签,通过推荐产品的属性解决新用户数据信息为零的问题,也可以将这些属性作为相似度计算所需数据,转换为基于内容的推荐。 SVD作为一种强大的降维和压缩工具,可以得到数据中的重要特征并去除冗余[23]信息,很大程度上保留了原有数据结构。作为机器学习中的一种基本算法,奇异值分解在信号处理、神经网络、水印处理、模式识别等方面也有广泛应用,是值得推荐和深度学习的一种算法。 参考文献: [1] 王腾飞. 推荐系统的改进[D]. 南京:南京大学,2018. [2] 王东. 基于用户与物品信息挖掘的矩阵分解推荐算法研究[D]. 西安:西安电子科技大学,2017. [3] 刘国枢. 基于局部全局相似度的奇异值分解的协同过滤算法研究[D]. 郑州:郑州大学,2016. [4] 陈亚雄,黄樟灿,冯磊. 基于奇异值分解和Contourlet变换的图像压缩算法[J]. 计算机应用研究,2017,34(1):317-320. [5] 李卫疆,齐静,余正涛,等. 融合信任传播和奇异值分解的社会化推荐算法[J]. 计算机工程,2017,43(8):236-242. [6] 余刚,王知衍,邵璐,等. 基于奇异值分解的个性化评论推荐[J]. 电子科技大学学报,2015,44(4):605-610. [7] 黄长春,徐抒岩,胡君. 奇异值分解遥感图像压缩算法研究[J]. 计算机仿真,2011,28(8):226-228,353. [8] 徐翔,王煦法. 基于SVD的协同过滤算法的欺诈攻击行为分析[J]. 计算机工程与应用,2009(20):93. [9] BOBADILLA J, ORTEGA F, HERNANDO A, et al. Recommender systems survey[J]. Knowledge-Based Systems,2013,46(1):109-132. [10] 张建军,陆国生,刘征宇. 基于奇异值分解和项目属性的推荐算法[J]. 合肥工业大学学报:自然科学版,2018,41(6):761-765,858. [11] 魏港明,刘真,李林峰,等. 加入用户对项目属性偏好的奇异值分解推荐算法[J]. 西安交通大学学报,2018,52(5):101-107. [12] JAMALI M,ESTER M.A matrix factorization technique with trust propagation for recommendation in social networks[C]. Proceedings of the 4th ACM Conference on Recommender Systems,2010: 135-142. [13] 王娟,林耀进,朱月秀. 联合奇异值分解与余弦相似性推荐的盲水印算法[J]. 小型微型计算机系统,2015,36(12):2784-2788. [14] RUFAI A M,ANBARJAFARI G,DEMIREL H. Lossy medical image compression using Huffman coding and singular value decomposition[C]. Proceedings of Signal Processing and Communications Applications Conference,2013: 1-4. [15] 王怀光,张培林,张云强,等. 基于奇异值分解和小波变换的图像压缩算法[J]. 火炮发射与控制学报,2012(4):38-42. [16] KHARATE, G K, PATIL, V H. Color image compression based on wavelet packet best tree[J]. International Journal of Computer Science Issues, 2010,7(4): 31-35. [17] 张晓锋,贾晓强. 基于奇异值分解的数字图像压缩技术研究[J]. 电子设计工程,2017,25(19):179-182,186. [18] 蒋卓芸,夏雪. 奇异值分解及其简单应用[J]. 成都大学学报:自然科学版,2015,34(4):364-366,370. [19] 王佳蕾,郭耀,刘志宏. 基于社交网络信任关系的服务推荐方法[J]. 计算机科学,2018,45(S2):402-408. [20] 林子扬. 基于相似度建模及SVD优化的协同过滤推荐引擎研究与设计[D]. 西安:西安电子科技大学,2017. [21] 魏琳东,黄永峰. 融合用户属性信息的冷启动推荐算法[J]. 电子技术应用,2017,43(10):137-140,144. [22] GANTNER Z, DRUMOND L, FREUDENTHALER C, et al. Learning attribute-to-feature mappings for cold-start recommendations[C]. 2010 IEEE 10th International Conference on Data Mining (ICDM), 2010:176-185. [23] 吴俊政. 一种基于奇异值分解的图像压缩方法[J]. 计算机与数字工程,2009,37(5):136-138. (责任编辑:孙 娟)

