我国新能源汽车月度销售量预测模型研究

周彦福 王红蕾

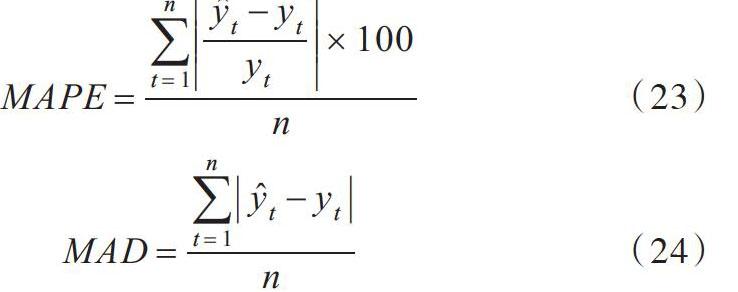
摘 要：在新能源汽车可缓解未来一系列环境、资源问题的重要背景下，对新能源汽车销售量准确预测有助于加速新能源汽车市场推广，降低相关生产研发企业运营成本。提取8个关键影响因素，应用灰色关联分析（GRA）验证各因素影响能力，然后构建基于果蝇算法优化灰色神经网络（FOA-GNN）预测模型的新能源汽车月度销售量预测模型。通过预测结果对比检验，验证该预测模型在预测新能源汽车销售量上有较高的预测精度。应用该模型对我国新能源汽车2019年月度销售量进行预测，结果表明，我国新能源汽车发展在2019年度依然可保持良好的增长态势。

关键词：新能源汽车;销售量;果蝇算法;灰色神经网络;销售量预测

DOI：10. 11907/rjdk. 191585 开放科学（资源服务）标识码（OSID）：

中图分类号：TP319文献标识码：A 文章编号：1672-7800（2019）008-0149-05

Research on Monthly Sales Forecasting Model of New Energy Vehicles in China

ZHOU Yan-fu，WANG Hong-lei

（School of Management， Guizhou University， Guiyang 550003， China）

Abstract： Under the background of important measures to alleviate a series of environmental and resource problems in the future， the accurate forecast of new energy vehicle sales can accelerate the promotion of new energy vehicles and reduce the operating costs of production and research-related enterprises. This paper extracts eight key influencing factors， and uses gray relevance analysis （GRA） to verify the influencing ability of each factor， and then constructs a new energy vehicle monthly sales forecasting model based on FOA-GNN prediction model. Through the comparison test of prediction results， it is verified that the prediction model has higher prediction accuracy in predicting the sales volume of new energy vehicles. Finally， the model is used to forecast the monthly sales volume of new energy vehicles in China in 2019. The results show that the development of new energy vehicles in China still maintains a good growth trend in 2019.

Key Words： new energy vehicle; sales volume; fruit fly algorithm; grey neural network;  sales volume prediction

基金項目：南方电网资助项目（066601（2016）030101XT198）

作者简介：周彦福（1994-），男，贵州大学管理学院硕士研究生，研究方向为管理系统工程;王红蕾（1959-），男，贵州大学管理学院教授、博士生导师，研究方向为管理系统工程。本文通讯作者：王红蕾。

0 引言

近年来，世界各国都面临能源短缺、环境污染严重、温室效应加剧等影响人类生存发展的重大问题，新能源汽车的推广和使用成为缓解该系列问题的重要举措之一。燃油汽车的使用需要消耗大量化石能源，且排放大量废气，造成资源枯竭和环境污染。使用新兴清洁能源作为主要动能的汽车对环境造成的污染远小于燃油汽车，现今大批量应用在汽车领域的新能源是电能，虽然电力在生产过程中会造成一定的能源消耗和污染，但是新能源汽车的使用不会产生污染，是替代燃油汽车的一种有效交通工具。

新能源汽车产销量在2018年有显著增长，从总产量上看，2018年总产量比2017增长了60.2%;从总销量上看，2018年比2017年增长了62.4%。由产销数据可知，我国新能源汽车在近几年发展非常迅速;但是从产销总量看，燃油汽车的生产与销售量仍然占所有汽车品类90%以上。所以新能源汽车研发、推广与使用依旧是一个重要研究问题。近年来在政府和企业的共同努力下，新能源汽车生产成本、行驶里程、资金投入和使用等关键问题获得重大突破。新能源汽车销售量预测对加速新能源汽车市场推广、降低生产研发相关企业的运营成本具有重要引导作用，对企业制订相关生产销售方案及扩大市场规模具有重要意义，也是企业销售管理的关键问题之一。

文献[1]采用偏好调查法分析未来动态市场对汽油、混合动力和纯电动汽车的偏好，把车辆购买价格、燃油经济性、充电范围和燃油价格作为动态变化的属性[1];文献[2]认为增加政府补贴政策，降低新能源汽车的生命周期成本，提高新能源汽车有效性，将提高消费者购买新能源汽车的意愿[2];文献[3]认为中国消费者决定是否购买新能源汽车最重要的影响因素包括产品内在品质、政府政策刺激、成本、参照群体和象征性因素[3]。

目前，銷量预测主要分为基于数学统计的方法与基于机器学习的方法。数学统计类方法依赖于产品历史销量数据，难以把握市场需求及产品生命周期[4]，预测精度不高，例如多元回归分析[5-6]、Holt-Winters方法[7-8]等。机器学习方法比数学统计方法的预测效果更佳，但是所需数据量较大，例如神经网络（Neural Network，NN）[9-10]、支持向量机[11]、机器学习[12]等。近年来，以多种预测技术、方法相结合的方式解决因技术、方法单一造成的预测误差较大的问题已成为预测模型研究热点[13-15]。

灰色系统理论（Grey System Theory，GST）主要用于处理“灰色”系统中存在的一系列问题[16]，所以GST用于预测难免出现较大误差。灰色神经网络（Gray Neural Network，GNN）继承了GST处理“贫信息”的能力与神经网络（Neural Network，NN）的学习能力，因此在处理相同数据并进行预测时，GNN更为准确。文献[17]提出了一种BP神经网络与灰色关联分析相结合的变权重系数组合预测模型，文献[18]提出一种果蝇算法优化的灰色神经网络模型，文献[19]提出一种动态粒子群算法优化灰色神经网络模型，文献[20]提出一种改进的多维灰色模型和神经网络的混合模型预测销量。

综上所述，本文针对新能源汽车销售数据较少、销售趋势与变化规律复杂、影响因素较多的情况，提取影响新能源汽车销售量关键影响因素，通过灰色关联分析并验证各因素的影响能力，再构建基于果蝇优化算法（Fruit Fly optimization algorithm，FOA）优化的GNN预测模型，使该预测模型在预测新能源汽车销售量时得出较高的预测精度。

1 相关理论介绍

1.1 灰色神经网络

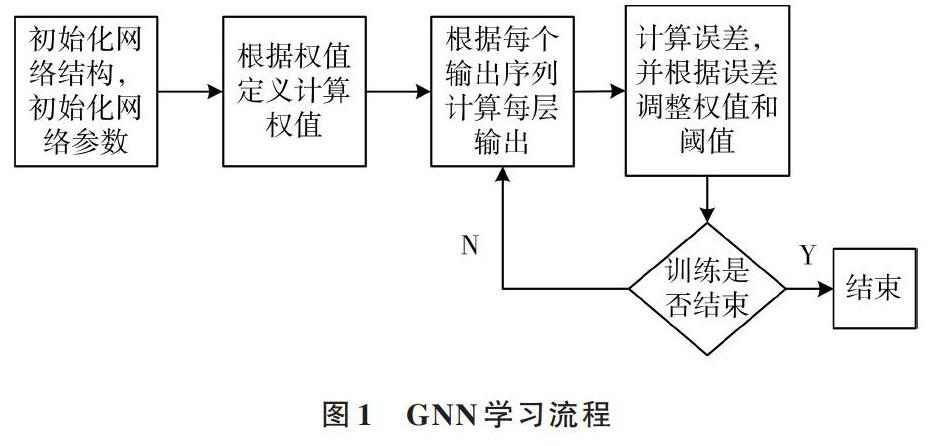
GST是研究难以完全采集到准确信息或采集信息量很少的情况下，对信息进行科学有效处理的理论。NN是对动物神经反应的特征进行数学仿真建立类似神经反应的数学模型。在应用层面上，两种方法都能够统计过去数据信息预测未来趋势，两者的不同在于灰色预测方法所需信息量较少，NN预测所需数据量较大。由于所需数据量不同，很难比较两种预测方法的优劣。在无法收集到大量准确且完整的数据时，又希望通过NN的不断学习进化实现良好的预测效果，于是产生了继承GST处理“贫信息”能力与NN学习能力的GNN模型。学习流程如图1所示。

图1 GNN学习流程

1.2 果蝇优化算法

该算法原理是根据果蝇能够高效地搜集漂浮在空气中的食物或者同伴的气味，然后飞向散发气味位置的这一特性推演而来。FOA数学仿真简要流程如图2所示。

图2 FOA流程

1.3 果蝇算法优化灰色神经网络预测模型

GNN预测模型的每次预测都会随机初始化该模型的权值阈值，造成该模型在训练中极易陷入局部最优，预测时出现预测结果不稳定等情况。FOA具备优秀的全局寻优能力，果蝇算法优化灰色神经网络（FOA-GNN）预测模型通过FOA对GNN预测模型中的权值阈值进行优化调整，使网络不易陷入局部最优的问题。简要流程如图3所示。

2 预测模型构建

2.1 灰色关联分析

灰色关联分析（Grey Relevance Analysis，GRA）是分析各影响因素之间发展趋势异同程度的方法，能够有效验证各影响因素的影响能力。相关公式如下：

[x0=x0（k）|k=1，2，？，n=（x0（1），x0（2），？，x0（n））] （1）

[xi=xi（k）|k=1，2，？，n=（xi（1），xi（2），？，xi（n）），]

[i=1，2，？，m]  （2）

[γi（k）=minsmintx0（t）-xs（t）+ηmaxsmaxtx0（t）-xs（t）x0（t）-xi（t）+ηmaxsmaxtx0（t）-xs（t）] （3）

其中，[k]表示时刻，[x0]表示参考数列，[xi]表示第[i]个比较数列;式（3）中[γi（k）]表示在[k]时刻，数列[xi]对[x0]的灰色关联系数;[η]表示分辨系数，取值区间为[0，1];两级最小差使用[minsmintx0（t）-xs（t）]表示;使用[maxsmaxtx0（t）-xs（t）]表示两级最大差。

通过式（4）计算数列[xi]对参考数列[x0]的关联度。

[ri=1nk=1nγi（k）]  （4）

2.2 模型构建

构建FOA-GNN模型步骤及相关计算公式如下。

（1）根据实际数据情况，确定GNN结构，继而能够确定训练参数[a，b，？，bi]，通过式（5）、（6）计算确定初始化GNN的权值、阈值。

图4 灰色神经网络拓扑结构

在图4中，t表示输入序列时间序号;[ω11，ω21，？，ω2n，][ω31，ω32，？，ω3n]分别表示各节点相互连接的网络权重;[y2（t），y3（t），？，yn（t）]分别表示各节点输入的带时间序号的输入序列，[y1]表示预测值，LA到LD分别表示网络的4层。相关公式如下：

[ω11=a，ω21=-y1（0），ω2m=2bm-1a，m=2，3，？，n] （5）

[ω3m=1+e-at，m=1，2，？，n] （6）

[a=ω11t] （7）

[b=f（a）=11+e-ω11t] （8）

[c1=bω21，cm=ym（t）bω2m，m=2，3，？，n] （9）

[d=j=1nω3jcj-θy1] （10）

[δ=d-y1（t）]  （11）

[δm=δ（1+e-ω11t），m=1，2，？，n] （12）

[δn+1=11+e-ω11t（1-11+e-ω11t）j=1nω2jδj] （13）

[ω21=-y1（0），ω2m=ω2m-2bm-1aδmb，m=2，3，？，n] （14）

[ω11=ω11+atδn+1] （15）

[θ=（1+e-ω11t）（12j=2nω2jyj（t）-y1（0））] （16）

[θ=（d-y1（0）））（1-e-at）] （17）

在式（5）-（17）中，[a、b、cm、d]分别表示LA层到LD层的输出，[δ]、[δ1、δm、δn+1]分别表示LD层到LB层的误差，使用[θ]表示阈值;式（7）-（10）用于计算LA层到LD层各节点的输出;式（11）-（13）用于计算LA层到LD层的实际输出与期望值的误差;式（14）、（15）用于计算调整后的权值;式（16）用于计算调整阈值;式（17）用于计算LD层输出节点的阈值。

（2）FOA相关参数设置如下：

[X_axis=rands（1，9）Y_axis=rands（1，9）]          （18）

[Xi=X_axis+10×rand（）-10Yi=Y_axis+10×rand（）-10]        （19）

[Dist（i）=Xi2+Yi2]            （20）

[S（i）=1Dist（i）]                  （21）

其中，式（18）表示果蝇群体的初始位置，[X_axis、][Y_axis]分别表示横纵坐标值，[rands（1，9）]表示随机取9个区间[0，1]的数值;式（19）表示果蝇个体飞行后位置，[Xi、Yi]分别表示果蝇个体[i]的横纵坐标值，[rand（）]表示随机取一个区间[0，1]的数值;[Dist（i）]表示果蝇个体[i]与原点的距离;[S（i）]表示气味浓度判定值。

在FOA-GNN程序设计中，使用[D（i，1），D（i，2），D（i，3），？，][D（i，n）]表示[Dist（i）]，[S（i，1），S（i，2），S（i，3），？，S（i，n）]表示[S（i）]，GNN中的参数[a，b1，b2，b3，？，bn-1]则由[S（i，1），S（i，2），][S（i，3），？，S（i，n）]表示。

（3）通过初步计算得出第一次迭代预测结果，并且可以求出气味浓度值Smelli（适应度函数）。气味浓度Smelli（适应度函数）由网络输出与期望值的误差平方和表示。保留气味浓度最佳值，即网络输出与期望值误差平方和最小值。

（4）通过果蝇迭代寻优不断更新气味浓度最佳值。不断重复第二、三步以实现迭代过程，直至达到设定的最大迭代次数，此时获得最佳参数与最优预测结果。

3 算例分析

3.1 数据选取

通过文献搜集及统计分析，选取新能源汽车产量、燃油汽车销量/产量、居民消费价格指数、消费者信心指数、人均国民收入、公共充电桩数量、汽油价格等作为影响新能源汽车销量的主要因素。

新能源汽车产量、燃油汽车销量/产量能反映新能源汽车销售趋势;居民消费价格指数、消费者信心指数、人均国民收入能够体现消费者消费水平和消费意愿强度，这些对于汽车这类大件销售是非常重要的影响因素;公共充电桩数量、汽油价格能够影响消费者在购买汽车时选择新能源汽车还是燃油汽车的意愿。

本文选择60个月份的相关数据，数据时间区间为2014年1月到2018年12月。其中80%是2014年至2017年共48个月作为预测模型的训练集，20%是2018年的12个月作为检验预测效果的测试集。新能源汽车/燃油汽车产量及销量数据通过中国汽车工业协会网站发布的数据与第一电动网及汽车工业协会统计信息网统计数据等处理得到。居民消费价格指数、消费者信心指数、汽油价格数据等来源于东方财富网数据库。人均国民收入数据来源于《中国统计年鉴》及国家统计局网站。公共充电桩数量数据通过查阅《中国电动汽车充电基础设施促进联盟年报》得出。

3.2 数据处理及模型建立

确定本文预测模型的网络结构为1-1-9-1，确定训练参数为[a，b，？，b8]。对新能源汽车产量、燃油汽车销量/产量、居民消费价格指数、消费者信心指数、人均国民收入、公共充电桩数量及汽油价格等8个影响因素的原始数据进行归一化处理，再进行累加后作为FOA-GNN模型的输入数据，将新能源汽车销量预测作为输出数据。算例中，果蝇种群规模设为20，迭代次数设为100，网络学习次数为10，学习速率设为0.001 5。在Matlab2016b中实现基于FOA-GNN模型的新能源汽车月度销售量预测，由于FOA的初始位置具有随机性，所以每次寻优得到的最佳参数往往不同，从而造成每次预测结果不同，所以本文算例预采用连续运行预测模型程序后得到50次预测结果的平均值作为该模型最终预测值。

3.3 模型预测分析

利用式（4）计算选取的8个影响因素数据序列与新能源汽车销量数据序列的灰色关联度，具體计算结果见表1。

由表可知，选取的8个影响因素中灰色关联度最小值也在77%以上，说明这8个影响因素均对新能源汽车销量有较大影响能力。因此可以把这8个影响因素作为灰色神经网络的输入变量。

表1 各影響因素灰色关联度

[影响因素＼&灰色关联度＼&影响因素＼&灰色关联度＼&新能源汽车产量＼&0.968 49＼&消费者信心指数＼&0.773 67＼&燃油汽车销量＼&0.772 87＼&人均国民收入＼&0.776 78＼&燃油汽车产量＼&0.774 09＼&公共充电桩数量＼&0.844 45＼&居民消费价格指数＼&0.813 14＼&汽油价格＼&0.769 61＼&]

本文使用平均绝对百分比误差（MAPE）和平均绝对偏差（MAD）两个误差值直观评价预测方法的预测效果。计算公式为：

[MAPE=t=1nyt-ytyt×100n]  （23）

[MAD=t=1nyt-ytn]  （24）

其中，第[t]月的实际销售量使用[yt]表示，第[t]月的预测销售量用[yt]表示，[n]表示预测的期数。

构建GNN预测模型、灰色预测模型和BP神经网络（BPNN）预测模型与该模型进行对比。图5呈现了4种预测模型预测值与实际值对比情况。不难发现，4种预测模型在前5个月的预测值都较为贴近实际值，表明4种预测模型在前5个月的预测效果相近。在5-8月阶段，实际值出现较大反常波动，BPNN出现较大偏差，这反映出BPNN在数据量不够大、训练不够好的情况下，预测反常波动会出现较大误差;在10-12月阶段，GNN、灰色预测、BPNN出现较大偏差，反映这3种预测模型在长期预测中均存在不足，虽然FOA-GNN在预测12月分值时也出现较大偏差，但是还是要优于其它3种预测模型。

图5 4种预测值与实际值对比

通过4种模型预测值计算得到的各自MAPE和MAD值如表2所示，从表中可以发现4种预测模型中，灰色预测模型无论是MAPE还是MAD都是最大的，所以可知其预测效果是4种模型中最差的，GNN预测模型与BPNN预测模型的MAPE和MAD相近，GNN预测预测效果略优于BPNN，FOA-GNN预测模型的MAPE和MAD都是最小的，所以可知其预测效果优于其它3种预测模型，验证了该优化模型适合应用于新能源汽车销售量预测。

表2 误差对比

使用FOA-GNN模型预测新能源汽车2019年12个月份的销售量情况，预测结果如表3所示。

表3 2019年月度销售量预测

2016年11月，由国务院发布的《“十三五”国家战略性新兴产业发展规划》明确指出，到2020年我国新能源汽车产销规模需突破200万辆大关[21]。由表3数据可知，2019年12个月的累计销售量预测约为197.3万量，逼近200万量的销量大关。2019年预测年销售总量比2018销售总量增长了58.1%，增量相对于2018年的62.4%少4个百分点，但仍然是非常可观的增长量。结合近年来我国新能源汽车发展形势来看，在2020年突破200万量的产销规模势在必行。

4 结语

现阶段我国新能源汽车发展仍不够成熟，消费者对新能源汽车的认知度还处于较低水平，政府与企业在新能源汽车的研发与推广处于高投入、低收益的状态。因此准确预测新能源汽车销售情况，能够有效加速新能源汽车产业发展，对降低研发与生产团队的运营成本具有重要引导作用，对相关企业制订生产销售计划及扩大市场规模具有重要意义。新能源汽车销售情况的影响因素复杂多样，本文从中提取了影响新能源汽车销售量的8个关键因素，并对影响因素进行灰色关联分析验证各因素的影响能力，构建FOA-GNN预测模型，并验证了该预测模型在新能源汽车销售量预测中的相对准确性。利用FOA-GNN预测模型对我国新能源汽车在2019年度销售情况进行预测，预测结果可为政府制定补贴政策、新能源汽车推广和企业的研发、生产和销售提供一定的参考依据。

参考文献：

[1] CINZIA C，LIU Y，MICHAEL M. A time-dependent stated preference approach to measuring vehicle type preferences and market elasticity of conventional and green vehicles[J]. Transportation Research Part A-Policy and Practice，2017，100：294-310.

[2] GUAN X，ZHANG G X，LIU D. The behavior of consumer buying new energy vehicles based on stochastic evolutionary game[J]. Filomat，2016，30（15）：3987-3997.

[3] WANG Z H，WANG C，HAO Y. Influencing factors of private purchasing intentions of new energy vehicles in China[J]. Journal of Renewable and Sustainable Energy，2013，5（6），063133，1-14.

[4] MEERAN S，JAHANBIN S. When do changes in consumer preferences make forecasts form choice-based conjoint models unreliable[J]. European Journal Of Operational Research，2017，258（2）：512-524.

[5] APADULA F，BASSINI A， ELLI A，et al. Relationships between meteorological variables and monthly electricity demand[J]. Applied Energy，2012，98（5）：34-356.

[6] 张新顺，王红军，马锋，等. 基于多元回归分析的致密油可采资源评价方法[J]. 石油与天然气地质，2018，39（6）：1323-1335.

[7] TRATAR L F，STRMCNIK E. The comparison of Holt-Winters method and multiple regression method：a case study[J]. Energy，2016，109：266-276.

[8] 李辉杰，刘悦春. 基于Holt-Winters模型的电网企业售电量预测方法[J]. 中国电力企业管理，2018（24）：86-87.

[9] RELICH M. New frontiers in information and production systems modelling and analysis[M]. Berlin： Springer，2016.

[10] 董丽丽，费城，张翔，等. 基于LSTM神经网络的煤矿突水预测[J]. 煤田地质与勘探，2019（2）：137-143.

[11] 刘璐，丁福利，孙立民. 基于SVM的烟草销售量预测[J]. 软件导刊，2016，15（11）：134-137.

[12] 李慧，张南南，曹卓，等. 基于机器学习的恐怖分子预测方法研究[J/OL]. 计算机工程：1-7[2019-04-30]. https：//doi.org/10.19678/j.issn.1000-3428.0053521.

[13] 苏振宇，龙勇，汪於. 基于季节调整和Holt-Winters的月度负荷预测方法[J]. 中国管理科学，2019，27（3）：30-40.

[14] 陈渝，任正军. 融合EMD与LSTM神经网络的门诊量预测模型研究[J]. 软件导刊，2019，18（3）：133-138.

[15] 宫毓斌，滕欢. 基于GOA-SVM的短期负荷预测[J/OL]. 电测与仪表：1-6[2019-04-30]. http：//kns.cnki.net/kcms/detail/23.1202.TH.20190425.1646.008.html.

[16] 李俊峰. 灰色系统建模理论与应用研究[D]. 杭州：浙江理工大学，2005.

[17] 李芬，李春阳，糜强，等. 基于GRA-BPNN时变权重的光伏短期出力组合预测[J]. 可再生能源，2018，36（11）：1605-1611.

[18] 张崇娇，沈小林，霍双红，等. 基于果蝇算法优化灰色神经网络的冰箱订单需求预测研究[J]. 數学的实践与认识，2017，47（20）：15-19.

[19] 章杰宽，朱普选. 动态粒子群算法优化灰色神经网络的旅游需求预测模型研究[J]. 管理评论，2013，25（3）：60-66.

[20] 黄鸿云，刘卫校，丁佐华. 基于多维灰色模型及神经网络的销售预测[J]. 软件学报，2019（4）：1031-1044.

[21] 中华人民共和国中央人民政府网. 国务院关于印发“十三五”国家战略性新兴产业发展规划的通知[EB/OL]. http：//www.gov.cn/zhengce/content/2016-12/19/content_5150090.htm，2016-12-19.

（责任编辑：江 艳）