航摄影像特征点提取算法研究
冯宇 朱大明 胡琳 张勇
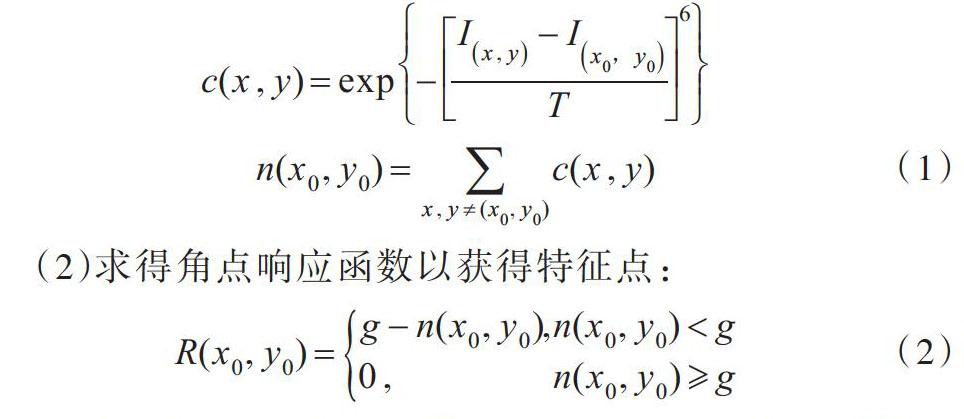


摘 要:随着无人机在测绘领域的广泛应用,航摄影像处理已成为国内外关注的热点。为寻求更适合航摄影像特征点提取的算法,对目前国内外几种常用特征点提取算法进行对比分析,结果表明,Moravec算子相较于其它算子,原理最为简单,但图像处理效果不佳。为此,利用C#工具实现Moravec算子,并通过图像处理实验,从计算速度、提取质量、定位精度、抗噪能力等方面对其进行全面分析,得出该算子在提取质量、定位精度与抗噪能力等方面均性能较差,该结论为今后对其优化改进提供了明确的研究方向。
关键词:航摄影像;图像特征;特征点提取;Moravec算子
DOI:10. 11907/rjdk. 182866 开放科学(资源服务)标识码(OSID):
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2019)008-0066-05
Research on Feature Point Extraction Algorithm
Based on Aerial Photography Image
FENG Yu, ZHU Da-ming, HU Lin, ZHANG Yong
(Faculty of Land and Resources Engineering, Kunming University of Science and Technology, Kunming 650093,China)
Abstract:With the wide application of UAV in the field of surveying and mapping, aerial image processing has become a hot topic at home and abroad. In order to find an algorithm suitable for feature extraction of aerial photography features, this paper extracts several common feature points at home and abroad. The algorithm performs in-depth comparative analysis and research. The results show that the Moravec operator algorithm is the simplest compared to other algorithm principles, but the image processing effect is not good. For this reason, for the performance of Moravec operator, the operator implementation is carried out by using C# tool, and the experimental research of image processing is carried out by using this operator. From the aspects of calculation speed, extraction quality, positioning accuracy and anti-noise ability, The analysis shows that the operator has poor performance in terms of extraction quality, positioning accuracy and anti-noise ability. This conclusion provides a clear research direction for the algorithm of optimizing Moravec operator in the future.
Key Words: aerial photography;image feature;feature point extraction;Moravec operator
作者簡介:冯宇(1994-),男,昆明理工大学国土资源工程学院硕士研究生,研究方向为地理信息技术开发与应用;朱大明(1970-),男,博士,昆明理工大学国土资源工程学院副教授,研究方向为地理信息工程、3S集成、土地规划。本文通讯作者:朱大明。
0 引言
如今,航摄技术已得到了广泛应用,对航摄图像的处理技术也不断更新。图像处理技术主要分为3类:①传输与储存图像信息;②改善图像质量;③提取图像特征[1]。图像特征点提取是图像处理的基本操作,而点特征是图像最基本的特征。提取点特征的算子称为兴趣算子。近年来,国内外学者研究的提取算法可大致分为两类:①基于模板匹配的方法,需要设定一系列特征点模板(如角点、交叉点等),根据模板与所有图像子窗口的相似性,判断位于窗口中心的像元是否为特征点[2];②基于几何特征的方法[3],该算法有两种获取途径:一是依据图像边界曲率进行提取,二是直接依据图像灰度信息提取特征点。该方法简单易行,通常利用兴趣算子提取特征点。常用特征点提取算子有:Moravec算子、Forstner算子、Harris算子、SUSAN算子与SIFT算子等。然而,目前关于以上几种算法的性能比较研究很少。因此,本文对几种常用算法进行实验对比与分析,对算子性能进行评估,同时对Moravec算子进行深入分析,从而为算子优化提供方向。
1 图像特征点提取算子
图像特征点提取算子是用来提取数字图像中点特征信息而采用的方法,图像处理技术发展至今,学者们已提出了Forstner、Moravec、SUSAN等多种算子[4]。这些算子各有优劣,以各自的优势在图像处理中发挥着作用,同时也因自身缺陷而影响其使用范围的拓展。本文将对Forstner、Moravec、SUSAN、Harris 4种算子进行深入研究与分析。
1.1 SUSAN算子
SUSAN的原理是在事先经过灰度化处理的数字图像上,使用曲率和度检测图像特征点[3]。将圆形窗口中心内未被检测的像素点作为核心点,将窗口中心的像素灰度值与其邻域内其它像素的灰度值作差,如果差值小于设定阈值,即可认为该点与核心点灰度相同。按照该原理得到以下计算步骤:
(1)首先通过计算灰度值找出与窗口中心像素相近的像素个数[n(x0,y0)]:
[c(x,y)=exp-Ix,y-Ix0,y0T6]
[n(x0,y0)=x,y≠(x0,y0)c(x,y)] (1)
(2)求得角点响应函数以获得特征点:
[R(x0,y0)=g-n(x0,y0),n(x0,y0) g為阈值,一般为窗口模板大小的3/4,以获取的特征点为中心,与领域其它点进行比较,保留灰度值最大的点,得出特征点。 1.2 Moravec算子 Moravec算子对像素点沿上下左右及45°斜对角方向共8个方向进行灰度变化的方差计算,具有最小方差的值被作为兴趣点,根据兴趣值设置的阈值作为判断特征点的基础依据,即利用“兴趣算子”提取特征点[6],具体步骤如下: (1)计算像元兴趣值,假设像素中心(p,q),计算4个方向灰度差的平方和。 [I1=j=-kk=1(gp+j-gp+j+1,q)2I2=j=-kk=1(gp+j,q+j-gp+j+1,q+j+1)2I3=j=-kk=1(gp,q+j-gp,q+j+1)2I4=j=-kk=1(gp+j,q-j-gp+j+1,q-j-1)2] (3) 其中,K=INT(M/2),兴趣值取以上值([I1、I2、I3、I4])的最小值。 (2)将小于该阈值的兴趣点作为待选点。 (3)选择待选点中的极值点作为特征点,在设定的窗口模板中,在待选点中去掉非最大兴趣值的点,只留下一个最大值,确认该最大值为特征点[7]。 1.3 Harris算子 Harris算子是在Moravec算子基础上改进的一种算子。Moravec算子可分析图像上某区域在水平、垂直、正负对角线几个方向上的位移,并计算每个像素点灰度,Harris算子在此基础上拓宽了研究思路。 基本方法为:以目标像素点为中心并沿着其周围“↑↗→↘↓↙←↖”8个方向移动,计算8个方向上的灰度变化,以这些值的最小值作为与阈值比较的对象。具体步骤如下: (1)使用(-1,0,1)(-1,0,1)T算子计算图像像素点在水平与垂直方向上的梯度Ix、Iy,并获得自相关矩阵[M1]。 [M1=I2xIyxIyxI2y] (4) (2)求得[M1]中4个元素的值,并获得自相关矩阵[M2]。 [M2=M1?φxy=I2xIyxIyxI2y?φxy] (5) (3)计算高斯滤波与角点函数值。 [R=Det(M2)-kTr2(M2)] (6) Det([M2])为矩阵[M2]的行列式,tr([M2])为矩阵[M2]的轨迹,k为默认常数,一般取值为0.04~0.06。 (4)采用非极大值抑制法得到的极值点即为特征点。 1.4 Forstner算子 Forstner算子选取角点、圆点等作为特征点,在选择图像中尽可能小的点、圆点以及近似圆点作为特征点过程中,需要计算各像素点的罗伯特梯度与灰度协方差矩阵,以及图像中提取的兴趣值,然后抑制局部极小点[8]。具体算法如下: (1)计算差分算子,计算像素(x,y)在左右上下方向的灰度差分绝对值dg1~dg4。 [dg1=gx,y-gx+1,ydg2=gx,y-gx,y+1dg3=gx,y-gx-1,ydg4=gx,y-gx,y-1] (7) (2)将dg1~dg4按从低到高进行排序: [M=mindg1,dg2,dg3,dg4] (8) 根据设定的阈值提取初选点,若M>T,(x,y)则为初选点。 (3)计算“罗伯特梯度”: [Gu=?g∕?uGv=?g∕?v] (9) (4)计算协方差阵: [N=G2uGuGvGuGvG2V] (10) (5)确定初选点: [q=4detN(trN)2w=detNteN] (11) det N表示N的行列式,tr N表示N的轨迹。若q比假设阈值大,则该像素为初选点。最后,选取极值点作为特征点。基于权重ω,选取最大的初选点作为合适大小窗口ω中的特征点[9]。 2 特征点提取方法对比 采用不同算法提取特征点,实验结果对比得如表1所示。 表1 实验结果对比 3 Moravec算子程序实现 经过实验比较,可明显看出Moravec算子略逊色于其它算子。使用C#程序语言作为工具对该算子进行更深入的研究,以便于之后对其进行优化。 根据Moravec算法实现流程,运用C#程序设计语言,在分析算法原理的基础上,梳理出程序实现的基本步骤,具体步骤为:创建一个窗体应用程序,对数字图像获取像素的三原色值进行灰度计算。利用图像处理技术中提取像素点法,首先使用GDI+中的GetPixel方法,读取当前像素颜色,再按照公式[Gray(i,j)=0.299×R(i,j)+0.587×][G(i,j)+0.114×B(i,j)]计算灰度值。灰度化处理可以降低程序运算量。按照Morvaec算子的算法原理,通过计算4个方向的灰度差平方和寻求极值,并求取特征点。Moravec算法实现流程如图1所示。 关键代码如下: toolStripProgressBar1.Value=0; toolStripProgressBar1.Maximum=10; toolStripProgressBar1.Value=1; double[,]Value2=newdouble[curBitmap.Height,curBitmap.Width]; for(inti=2;i {for(intj=2;j {doubleV1=0; for(intm=0;m<4;m++) {V1=V1+Math.Pow(Value1[i-2+m,j]-Value1[i-1+m,j],2);} //计算V1方向相邻像素灰度差平方和 Value2[i,j]=Math.Min(Math.Min(Math.Min( V1,V2),V3),V4); toolStripProgressBar1.Value=3; doublesum=0; for(inti=0;i {for(intj=0;j {sum+=Value2[i,j];}} intp=0,Strength=0;u=1100;doublerange; Co=newint[img1.Height*img1.Width/9,2]; double[,]Value3=newdouble[img1.Height,img1.Width]; doubleavg1=sum/((img1.Height-2)*(img1.Width-2)); range=avg1; while(u>1 000||u<1) {if(u>1 000) {Strength++;range=avg1*Strength;} else {range=range*((2*Strength-1)/2*Strength);} for(inti=0;i for(intj=0;j {if(i==0||i==1||i==img1.Height-2||i==img1.Height-1||j==0||j==1||j==img1.Width-2||j==img1.Width-1) {Value3[i,j]=0; continue;} else {if(Value2[i,j]>range) {Value3[i,j]=1;p=p+1;} else Value3[i,j]=0;}//检索图像兴趣点,存储5*5模板灰度 if(MAX>0) {Co[u,0]=a;Co[u,1]=b;u=u+1;}}} toolStripProgressBar1.Value=8; Templet=newdouble[u,25]; for(inti=0;i {intt=0; for(intm=0;m<5;m++) {for(intn=0;n<5;n++) {Templet[i,t]=Value1[Co[i,0]-2+m,Co[i,1]-2+n];// t++;} 在上述过程中,通过给定阈值将大于阈值的点筛选出来,并在模板5*5窗口中选取极值点作为特征点;然后利用函数GDI+中的Graphics类将提取的特征点绘制在图像上,使用三次插值在图像上绘制特征点,如图2所示;最后,通过代码实现同名像点匹配。本文采用相关系数法识别两幅图像中的特征点,并通过计算相关系数进行图像匹配,在此不再赘述[8]。测试运行特征点提取结果与先经过灰度处理再进行图像匹配的结果如图3、图4所示。 图2 使用三次插值在图像上绘制特征点效果 图3 特征点提取结果 图4 先经过灰度处理再进行图像匹配结果 4 实验结果分析 操作菜单下有两个选项,图像特征点提取操作与同名点匹配操作。接下来采用建筑楼的航摄影像进行实验,结果如图5、图6所示。 图5 楼1图像处理 图6 楼2图像处理 由图5、图6实验结果可知,对于采用相关系数法的图像匹配,特征比较明显的地方图像配准度较高,不明显的地方则匹配不够准确。 对Forstner、SUSAN、Harris、Moravec 4种算子的优点及不足进行对比分析,对比结果如表2所示。 表2 各种算子对比结果 由以上实验结果可得,Moravec算子计算过程简单,但提取的特征点因受到噪声影响变化很大;其次,阈值大小的设定是影响点提取效果的一个重要因素,图像本身纹理特征对结果影响也较大。该程序对于较大图像的处理速度比对比实验中使用的程序慢得多。 5 结语 图像特征点提取是数字图像处理中非常重要的步骤,目前已在遥感、医学、计算机视觉甚至公安等领域得到了成功应用。随着现代科技的发展,图像处理技术应用也更加广泛,同时也面临新的挑战。本文通过对各种特征点提取的算子原理进行学习,然后对航拍影像的特征点提取进行实验,对各种算子的優点及不足进行对比分析。其中,算法计算方式、阈值设置会对提取效果造成很大影响,其次图像纹理、旋转变换等也会影响提取效果。 通过对各算子的对比分析,Forstner、SUSAN、Harris算子在计算速度、提取质量、定位精度、抗噪能力方面各有优势,但算法也相对复杂;Moravec算子最为简单,但其在图像特征点提取质量与抗噪能力方面表现最差。因此,下一步将结合Moravec算子原理简单的优点,对其图像特征点提取质量与抗噪能力等进行优化。同时,对几种算子进行综合与改进,也是今后的重点研究方向。 参考文献: [1] 赵春江. C#数字图像处理算法典型实例[M]. 北京:人民邮电出版社, 2009. [2] 张祖勋,张剑清. 数字摄影测量学[M]. 武汉:武汉测绘科技大学出版社,1997. [3] 刘阳,邹峥嵘. 摄影测量中几种特征点提取算法比较[J]. 测绘与空间地理信息,2012,35(8):219-221. [4] 鲍军肖. 基于特征点和互信息的医学图像配准研究[D]. 秦皇岛:燕山大学,2010. [5] 肖飞. 基于图像特征提取和特征点描述的匹配算法研究及其应用[D]. 成都:电子科技大学,2013. [6] 侯艳杰. 侦察图像的拼接与地图匹配技术研究[D]. 南京:南京航空航天大学,2011. [7] 张晓芳. 基于双目立体视觉非接触物体测量的研究[D]. 大连:大连理工大学,2009. [8] 潘启龙. 无源毫米波探测成像系统目标检测与识别方法[D]. 成都:电子科技大学,2014. [9] 官云兰,张红军,刘向美. 点特征提取算法探讨[J]. 东华理工学院学报,2007 (1):42-46. [10] 陈淑荞. 数字图像特征点提取及匹配的研究[D]. 西安:西安科技大学,2009. [11] 肖若秀. 图像匹配方法研究与应用[D]. 昆明:昆明理工大学,2008. [12] 李先怡. 特征点匹配技术在无人机影像匹配中的研究与应用[D]. 西安:西安科技大学,2011. [13] 赵悟. SIFT与Harris算法在图像特征点提取中的适用性研究[D]. 济南:山东师范大学,2016. [14] 赵艳丽. 图像特征提取与匹配算法研究[D]. 成都:电子科技大学,2011. [15] 杨晓晖,宁彦俊,王文娟,等. GD09-069图像特征点提取角点量阈值自适应选取方法[C]. 第10届全国光电技术学术交流会论文集,2012:263-263. [16] 王舒鹏,方莉. 利用Moravec算子提取特征点实现过程分析[J]. 电脑知识与技术:学术交流,2006 (9):125-126. [17] 杨晓敏,吴炜,卿粼波,等. 图像特征点提取及匹配技术[J]. 光学精密工程,2009,17(9):2276-2282. [18] RODRIGUEZ J J, AGGARWAL J K. Matching aerial images to 3-D terrain maps[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1990, 12(12):1138-1149. [17] BROWN L G. A survey of image registration techniques[J]. Acm Computing Surveys, 1992, 24(4):325-376. [18] 柴进. 航空摄影测量特征点提取与匹配算法研究[C]. 第七届图像图形技术与应用學术会议论文集,2012:44-53. (责任编辑:黄 健)

