高效图推荐算法应用研究
刘清 王帆 冯亮 夏天鹤 熊志奇 施涛
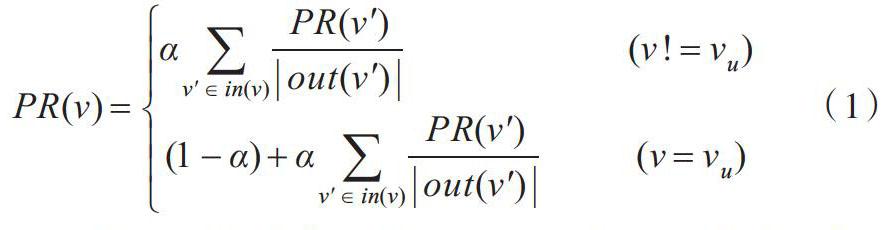
摘 要:为解决PersonalRank图推荐算法在推荐系统应用中的效率问题,从降低时间复杂度和减少迭代次数两方面进行算法优化。首先,构建推荐系统中用户行为数据二分图和迭代推荐模型;然后,建立转移矩阵,通过矩阵运算转换传统迭代模型,求解稀疏矩阵线性方程组直接得到系统稳态,有效降低了推荐算法的时间复杂度;最后,通过确定游走概率,在不影响系统精度前提下,各节点概率值收敛前就提前停止迭代,大幅减少了系统迭代次数。实验表明,转移矩阵法推荐效率比传统迭代法提高了211倍左右,游走概率取值为0.1时精度趋于稳定。优化后的算法能有效提高推荐效率。
关键词:图推荐;转移矩阵;游走概率;PersonalRank
DOI:10. 11907/rjdk. 191298 开放科学(资源服务)标识码(OSID):
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2019)008-0049-03
Research on the Application of Efficient Graph Recommendation Algorithm
LIU Qing, WANG Fan, FENG Liang, XIA Tian-he, XIONG Zhi-qi, SHI Tao
(China Xi'an Satellite Control Center, Xi'an 710043,China)
Abstract: In order to solve the efficiency problem of the recommendation algorithm of PersonalRank graph in the application of the recommendation system, the algorithm optimization is carried out from two aspects of reducing the time complexity and the number of iterations. Firstly, a binary graph of user behavior data and an iterative recommendation model are constructed. Then, the transfer matrix is established, and the traditional iterative model is transformed by the matrix operation. The steady state of the system can be directly obtained by solving the linear equations of the sparse matrix, which can effectively reduce the time complexity of the recommendation algorithm. Finally, by determining the walk probability, on the premise of not affecting the accuracy of the system, the iteration of each node is stopped before the probability value converges, and the number of system iterations is greatly reduced. It can be seen from the experiment that the recommendation efficiency of the transfer matrix method is about 211 times higher than that of the traditional iterative method. When the walk probability is 0.1, the accuracy tends to be stable. The optimized algorithm can effectively improve the efficiency of recommendation.
Key Words: graph recommendation; transfer matrix; walk probability; PersonalRank
作者簡介:刘清(1982-),男,硕士,中国西安卫星测控中心工程师,研究方向为云计算、航天测控;王帆(1982-),男,硕士,中国西安卫星测控中心工程师,研究方向为航天器轨道计算;冯亮(1980-),男,硕士,中国西安卫星测控中心工程师,研究方向为航天器测控;夏天鹤(1988-),男,中国西安卫星测控中心助理工程师,研究方向为航天测控;熊志奇(1992-),男,中国西安卫星测控中心助理工程师,研究方向为北斗导航;施涛(1988-),男,中国西安卫星测控中心高级技师,研究方向为供配电。本文通讯作者:王帆。
0 引言
随着互联网的发展,人类从信息匮乏时代走进信息过载时代,信息消费者越来越难于从海量信息中找到自己感兴趣的信息[1-2] ,信息生产者也难于确保生产的信息能够得到广大用户关注[3-4]。随着数据挖掘技术的发展,推荐算法逐渐在学术研究和工程应用领域成为热点,推荐系统较好地解决了这一矛盾[5-6]。国外关于推荐应用的研究起步较早[7-9],国内近年来也有涉及[10-13],但因算法时间复杂度过高,推荐效率直接制约着推荐算法的推广应用。推荐的实现主要有基于用户行为数据、内容标签数据和社交网络信息等方式[14-17]。基于用户行为数据的推荐包括协同过滤、基于图模型和基于矩阵填充3种推荐算法[18-19]。PersonalRank 算法是一种图模型推荐算法[20],能够较好实现信息推荐。本文在研究PersonalRank 算法基础上,从降低时间复杂度和减少迭代次数两方面进行算法优化,以有效解决推荐系统效率不高问题。
1 Personal Rank算法
PageRank算法是一种随机游走算法[20],能为一张图的每个节点求得一个反映这个节点在图中重要程度的权值。如果该图是强连通的,那么随机游走必然会收敛[20]。PersonalRank算法是PageRank算法的变形,是一种典型的图推荐算法,增加了用户的个性化,考虑了不同用户下的最大可能性,在度量节点间相似程度方面得到应用。在推荐系统中,用户行为数据可以表示成图的形式。行为数据集由一系列(u,i)二元组组成,表示为用户u对物品i产生过行为。假设用户对产生过行为的物品兴趣度相同,则只考虑“感兴趣”和“不感兴趣”两种状态。
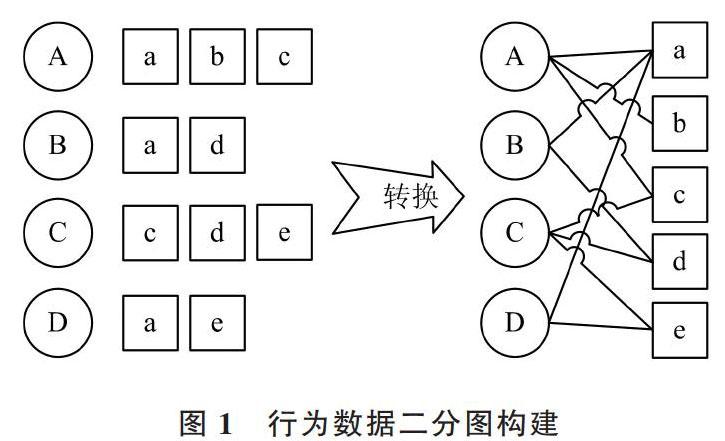
使用PersonalRank算法对电商用户作商品推荐,使其能利用当前的访问行为数据向用户推荐将来可能感兴趣的商品。首先要将用户和商品信息构建成一张二分图。二分图中有两类节点,一类是代表用户的节点,一类是代表商品的节点。当某个用户访问过一个商品时,就将两者之间连一条边,构成二分图[21] ,过程如图1所示。
图1 行为数据二分图构建
图1中,圆形节点代表用户,方形节点代表商品,圆形节点和方形节点之间的边代表用户对商品的访问,图中用户A和商品节点a、b、c 相连,说明用户A有对a、b、c商品的访问行为。令G(V,E)表示用户商品的二分图,其中V=Vu∪Vi,由用户顶点集合Vu 组成。对于数据集中的每一个二元组(u,i),图中都有一套对应的边e(vu,vi),其中vu∈Vu 是用户u对应的顶点,vi∈Vi是商品中i对应的顶点。
由于PersonalRank算法不区分用戶节点和商品节点,并假设每条边代表感兴趣程度相同,当需要为用户A推荐商品时,实际上就转化为计算用户A相对于节点A、B、 C、 D、a、b、c、d、e的重要度各是多少。
重要度用PR表示,初始赋值为0。即对于A来说,其自身的重要度为1,其它节点的重要度均为0。计算重要度时,首先选中一个节点作为计算与其重要度的中心节点,然后开始在图上游走。每次游走都是从PR不为0的节点开始,往前随机游走一步,然后按照一定的游走概率决定继续游走到下一节点或返回中心节点。游走概率用α表示,继续游走的概率是α,停留在当前节点的概率是1-α。如果决定继续游走,那么游走到相邻接点的概率按算法迭代计算。这样经过多次迭代,每个节点的权值会收敛到一个固定值,这个权值就是其与中心节点的重要度,如公式(1)所示。
[PR(v)=αv∈in(v)PR(v)out(v) (v!=vu)(1-α)+αv∈in(v)PR(v)out(v) (v=vu)] (1)
其中,u和v是待推荐的节点,PR(v)是v节点的权值,α是继续游走的概率,out(v)是v节点的出边,in(v)是v节点的入边。
不同节点重要度随着迭代过程不尽相同,会在一定次数迭代计算后收敛,收敛后每个节点的权重表示该点的重要程度,此时选择用户A没有产生过商品访问行为中重要度最大的一个商品向用户A推荐。
2 推荐算法优化实验
虽然PersonalRank算法可通过随机游走进行较好的理论解释,但该算法在时间复杂度上有明显缺陷。当为每个用户进行推荐时,都需要在整个用户商品二分图上进行迭代,直到整个图上每个顶点的PR值收敛,这一过程的时间复杂度非常高,不仅无法在线提供实时推荐,甚至离线生成推荐结果也非常耗时。为解决算法时间复杂度高的问题,可从降低时间复杂度和减少迭代次数两个方面进行优化。
2.1 降低时间复杂度
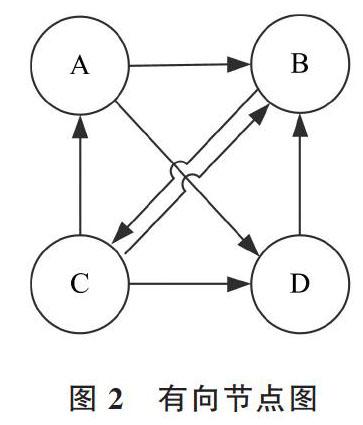
为解决时间复杂度过高问题,避免多次迭代游走,可以建立状态转移矩阵[21] 。从矩阵论出发,经过一次矩阵运算就可直接得到系统的稳态[22-23] ,能够有效降低时间复杂度。如图2所示的4个关系节点,每个节点的出边权值之和为1,可以建立如式(2)的转移矩阵。
图2 有向节点图
[001/301/201/3101001/201/30] (2)
该转移矩阵每一列表示一个节点出边的权重,例如第一列表示节点A的出边,它对B、D 两个节点分别有一条边,权重各为1/2。
这样,迭代公式(1)可转换为式(3)的矩阵表示形式。
[r = (1-α)r0+αMTr] (3)
其中,r是n维向量,每个元素代表一个节点的PR重要度;r0也是n维向量,第i个位置上是1,其余元素均为0;M是n阶转移矩阵。对于迭代公式(1)左边的PR(j)和PR(i),i是j一条入边,最终迭代概率(权重)在r中表示。当要为第i个节点进行推荐时,可表示为式(4)。
[Mij=1out(i) (j∈out(i)) 0 (j!∈out(i))] (4)
由式(3)变形可得到式(5):
[(1-αMT)r=(1-α)r0] (5)
因为M是稀疏矩阵,所以[1-αMT]也是稀疏矩阵[22]。因此,只需要一次[(1-αMT)-1]矩阵运算,就可通过解稀疏矩阵的线性方程组得到系统稳态。
推荐算法的衡量指标包括准确率(precision)、召回率(recall)、流行度(Popularity)和多样性(diversity)等,使用转移矩阵前后推荐指标对比如图3所示。
图3 实验结果对比
通过实验发现,不使用转移矩阵的传统迭代法经过46次迭代后,所有节点的概率值趋于收敛,用时9 647ms;根据状态转移矩阵,经过一次矩阵运算就可直接得到系统的稳态,计算出各节点的概率值用时45.7ms。由此结果可知,转移矩阵法的推荐效率比传统迭代法提高了211倍左右,推荐效果技术指标基本一致。因此,利用稀疏矩阵的线性方程解法,能有效降低推荐算法的时间复杂度,快速得出推荐结果。
2.2 减少迭代次数
在收敛之前就提前停止迭代,虽然可以减少迭代次数,但可能会因游走概率(α)的取值不同而影响最终精度。为探讨不同游走概率对算法的影响,通过实验测试不同α取值情况下算法的召回率、准确率和覆盖度变化情况,实验结果如图4所示。
从实验数据可知,算法精度总体上随着游走概率(α)的减少而变好。当取值为0.1时精度趋于稳定,算法效果最好。因此,设置游走概率为0.1时可在保证推荐精度前提下,大幅减少算法迭代次数,从而有效提高推荐效率。
图4 实验精度对比
3 结语
PersonalRank算法在推荐系统应用中的时间复杂度过高,影响推荐效率,可从降低时间复杂度和减少迭代次数两方面进行算法优化。本文研究发现,从矩阵论出发建立状态转移矩阵,经过一次矩阵运算就直接得到系统稳态,避免多次迭代过程,有效降低了时间复杂度;另一方面,选取游走概率为0.1时,在各节点概率收敛之前就提前停止迭代,既可保证精度,又能大幅减少迭代次数,提高操作效率。本文为推荐系统提供了一个高效的实现方法。
参考文献:
[1] HAN J,KAMBER M,PEI J. Data mining: concepts and techniques[M]. Morgan Kaufmann,2006.
[2] JANNACH D,ZANKER M,FELFERNIG A,et al. Recommender systems: an introduction[M]. Cambridge University Press,2010.
[3] KOREN Y,BELL R. Recommender systems handbook[M]. Advances in collaborative filtering. New York:Springer,2011.
[4] LIU T Y. Learning to rank for information retrieval[J]. Foundations and Trends in Information Retrieval, 2009, 3(3): 225-331.
[5] RICHARD HAMMACK,OWEN PUFFENBERGER. A prime factor theorem for bipartite graphs[J]. European Journal of Combinatorics,2015(4):542-549.
[6] CHEN L,CHEN G,WANG F. Recommender systems based on user reviews:the state of the art[J]. User Modeling and User-Adapted Interaction,2015,25(2):99-154.
[7] LU C,SHUAI H,YU P S. Identifying your customers in social networks[C]. Shanghai:Proceedings of the 23rd ACM International Conference on Information and Knowledge Management,2014.
[8] TAY D B H,LIN Z. Design of near orthogonal graph filter banks[C]. IEEE Signal Processing Letters,2015:701-704.
[9] RAKESH V,CHOO J,REDDY C K. Project recommendation using heterogeneous traits in crowdfunding[C]. Ninth International AAAI Conference on Web and Social Media,2015:1-10.
[10] 項亮. 推荐系统实践[M]. 北京:人民邮电出版社,2012.
[11] 许海玲,吴潇,李晓东,等. 互联网推荐系统比较研究[J]. 软件学报,2009,20(2):350-362.
[12] 王子政,姚卫东. 一种改进的组合推荐算法研究[J]. 军民两用技术与产品,2015(23):46-47.
[13] 刘琳竹. 基于数据挖掘的个性化推荐算法研究[D]. 北京:北京理工大学,2016.
[14] 裴中佑. 基于随机游走的推荐技术研究及应用[D]. 成都:西南交通大学,2014.
[15] 吴迪. 高校毕业生就业推荐系统的设计与开发[D]. 大连:大连理工大学,2010.
[16] 金连旭. 面向企业的高校毕业生就业推荐算法研究[D]. 济南:山东师范大学,2017.
[17] 金连旭,王洪国,丁艳辉,等. 基于兴趣敏感度的高校毕业生就业推荐算法[J]. 计算机与数字工程,2017(2):201-205,253.
[18] 魏丽芹. 基于历史信息的就业推荐算法研究与可视分析[D]. 济南:山东大学, 2013.
[19] 陈天,刘文浩. 相似度算法分析与比较研究[J]. 现代计算机:专业版,2012(18):18-20.
[20] 吴迪,周利娟,林鸿飞. 基于随机游走的就业推荐系统研究与实现[J]. 广西师范大学学报:自然科学版:2011(1) :179-185.
[21] 王伟,陈伟,祝效国,等. 众筹项目的个性化推荐:面向稀疏数据的二分图模型[J]. 系统工程理论与实践,2017(4):1011-1023.
[22] 黄谭,苏一丹. 基于混合用户模型的二分图推荐算法[J]. 计算机技术与发展,2014(6):145-148,152.
[23] 张绍飞. 矩阵论教程[M]. 北京:机械工业出版社,2012.
(责任编辑:杜能钢)

