加权三支决策增量软聚类算法及性能分析
申彦博 袁洁 纪淑娟 张纯金


摘 要:现有的增量聚类算法虽然解决了数据增量和类簇重叠问题,但在距离度量时没有考虑属性重要度不同,且普遍拥有较高的时间复杂度。针对以上问题,提出一种基于属性重要度的加权三支决策增量软聚类算法(W-TIOC-TWD算法),将属性重要度考虑到距离度量中,弥补了现有算法在聚类过程中将所有属性的重要程度视为相等的不足。该算法还引入离群点概念,降低了算法的时间复杂度。基于人工数据集和UCI数据集的实验结果表明,W-TIOC-TWD算法的聚类准确率优于比较算法。
关键词:聚类分析;增量聚类;离群点;三支决策理论;属性重要度
DOI:10. 11907/rjdk. 191251 开放科学(资源服务)标识码(OSID):
中图分类号:TP312 文献标识码:A 文章编号:1672-7800(2019)008-0042-07
A Weighted Three-way Decision Incremental Clustering Algorithm
and Performance Analysis
SHEN Yan-bo1,YUAN Jie1,JI Shu-juan1,2,ZHANG Chun-jin3
(1. College of Computer Science and Engineering, Shandong University of Science and Technology;
2. Key Laboratory for Wisdom Mine Information Technology of Shandong Province, Shandong University of Science and Technology;
3. Network Information Center, Shandong University of Science and Technology, Qingdao 266590,China)
Abstract:Though the existing incremental clustering algorithms can solve the problem of data increment and class overlap, those algorithms do not consider the difference of attribute importance in distance measurement and generally have a higher time complexity. To solve the above problems, this paper proposes the W-TIOC-TWD algorithm. Taking attribute importance into the calculation of distance measure, this algorithm can cover the shortage that equally regard the importance of all attributes in the process of clustering. Moreover, the definition of outlier point is proposed, which improves the time efficiency of this algorithm. To verify the effectiveness and accuracy of this algorithm, experiments on artificial datasets and UCI datasets are implemented. Experimental results show that the W-TIOC-TWD algorithm outperform the comparison algorithms.
Key Words:clustering analysis; incremental clustering; outlier point; three-way decision theory; attribute importance
基金项目:国家自然科学基金项目(71772107,71403151,61502281,61433012);青島社会科学规划研究项目(QDSKL1801138);山东省重点研发计划项目(2018GGX101045);山东省自然科学基金项目(ZR2018BF013,ZR2013FM023,ZR2014FP011);山东省研究生质量提升计划项目(2016);山东科技大学领军人才计划项目(2014);泰山学者攀登计划项目(2014)
作者简介:申彦博(1994-),男,山东科技大学计算机科学与工程学院硕士研究生,研究方向为人工智能与智能商务信息处理;袁洁(1992-),女,山东科技大学计算机科学与工程学院硕士研究生,研究方向为人工智能与智能商务信息处理;纪淑娟(1977-),女,博士,山东科技大学计算机科学与工程学院、山东省智慧矿山信息技术重点实验室副教授、博士生导师,研究方向为人工智能与智能商务信息处理;张纯金(1977-),男,硕士,山东科技大学网络信息中心工程师,研究方向为智能信息处理和网络安全。
0 引言
聚类分析[1]作为一种常用的数据挖掘技术,广泛应用在推荐系统、话题追踪与检测等领域。传统的聚类算法大多是静态硬聚类算法,无法处理动态变化的数据,并且数据对象经过聚类后只能划分到唯一的类簇中,聚类准确率低。为此,人们提出了基于增量的聚类算法。这类算法基本特点是:增量数据到来后,只需在原聚类结果基础上对增量数据进行聚类,无需重新聚类整个数据集,从而避免了大量的重复计算。然而,增量聚类算法依然属于硬聚类算法,存在着数据对象只能划分到唯一类簇的局限性。软聚类算法则有效解决了这一问题,使得一个数据对象可以属于多个类簇。
基于树结构的三支决策增量聚类算法[2](TIOC-TWD算法)同时解决了数据增量和类簇重叠问题,但该算法在聚类时没有将属性重要程度考虑到距离计算公式中;此外,该算法将密度为1的点也标记为代表点,使构建搜索树以及增量更新时浪费大量时间。针对以上问题,本文提出一种基于属性重要度的加权三支决策增量软聚类算法(W-TIOC-TWD算法),将属性重要度考虑到距离度量中,弥补了TIOC-TWD算法在聚类过程中将所有属性的重要程度视为相等的不足,提高了聚类结果准确率;同时,本文对密度为1的点进行隔离,降低了算法的时间复杂度。
1 相关工作
为降低时间成本,提高聚类准确率,提高聚类算法动态处理变化数据集能力,解决数据对象重叠问题,研究人员提出了很多增量聚类算法和软聚类算法。
1.1 基于增量的聚类算法
Charkraborth等[3]将K-means算法应用到增量聚类中,对离增量数据最近的簇进行聚类操作;Pham等[4]提出一种基于目标优化的增量K-means聚类算法,能对大数据集快速进行增量聚类。但这两种算法都是基于K-means思想实现的,需要人为设定聚类个数并且算法只能发现球状类簇。
ALM等[5]对DBSCAN算法进行了扩展,提出了新的增量DBSCAN聚类算法,并使用有效性评测指标GDI和DB对聚类结果进行评价。实验结果表明增量DBSCAN聚类算法较传统的DBSCAN算法更有效率,但该算法仍未解决算法参数敏感问题。为解决DBSCAN算法受参数影响较大问题,刘青宝等[6]提出了一种基于相对密度的增量式聚类算法,但算法聚类形成的类簇都必须由全部数据组成,在进行增量更新时内存占用问题很难解决。
在基于网格的增量聚类研究中,LEI等[7]提出了新的增量聚类算法IGrid算法,算法基于网格对空间多维数据进行统计分析,利用网格聚类思想处理增量聚类问题,该算法可以发现任意形状的类簇;刘卓等[8]将网格聚类与数据流聚类相结合,使得网格聚类在数据流中得到进一步发展,但是基于网格的聚类算法仍无法解决参数敏感问题。
1.2 软聚类算法
二支决策硬聚类算法都存在不能发现重叠类簇的缺点。为满足应用领域对聚类的需求,人们提出了软聚类算法。Labroche等[9]提出了在线模糊中心聚类算法,该算法可以检测奇异数据对象和重叠的类簇,但需要人工指定数据集中最终的类簇个数;Peters等[10]提出了一种动态粗糙聚类算法,该算法主要使用粗糙集理论检测数据集结构的改变,且算法还定义了一些标准度量新增数据与已有数据对象间的结构一致性,并对增量数据进行聚类。但在实际数据处理过程中,这些判断标准很难确定;Perez-Suarea等[11]提出了一种基于图理论的动态重叠聚类算法DClustR,算法根据数据的密度相关性寻找一组节点完成图的覆盖,且只对受增量数据影响的图进行更新,但该算法的缺点是发现的类簇都比较小。
近几年提出的三支决策思想为解决重叠聚类问题提供了新思路。三支决策[12]是对传统二支决策的扩展,其在二支决策基础上增加了不承诺决策,即三支决策由接受、拒绝、不承诺3种决策组成,分别对应于粗糙集模型的正域、边界域和负域。于洪等[13]将三支决策思想与K-means算法相结合,提出了一种基于K-means的自动三支决策聚类方法,该算法能够发现重叠类簇,并能自动确定类簇个数。然而,该算法对聚类个数的确定依赖于近邻选取。
1.3 三支决策增量聚类算法(TIOC-TWD)
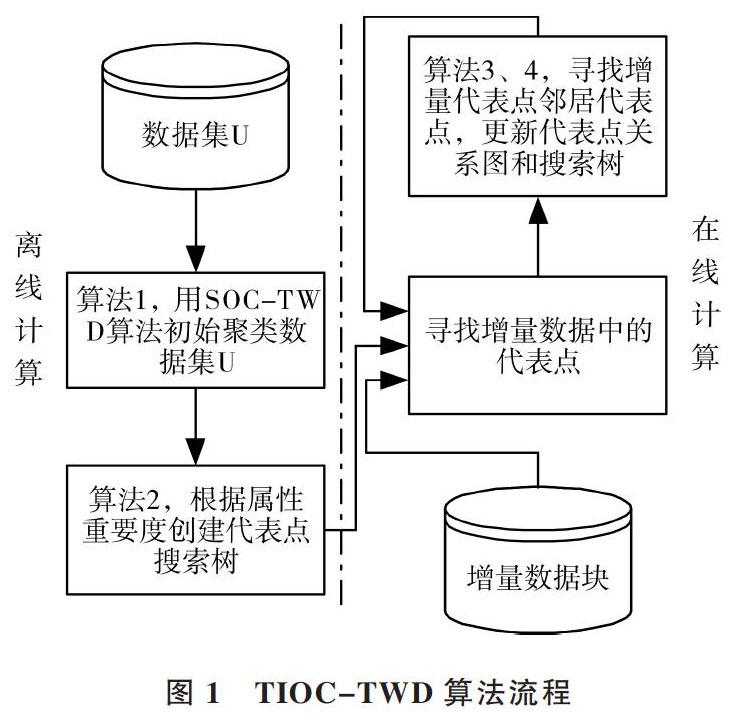
为解决上述问题,于洪等提出了基于树结构的三支决策增量聚类算法(TIOC-TWD算法)。图1展示了TIOC-TWD算法流程。TIOC-TWD算法由4部分组成,算法1、算法2采用离线计算方法,算法3、算法4采用在线计算方法。算法1为三支决策重叠聚类算法,采用欧式距离寻找数据集的代表点,对数据集进行初始聚类;算法2的主要任务是创建代表点搜索树;算法3的基本思想是在增量数据到来后寻找增量数据的邻居代表点;算法4是更新增量算法,更新代表点搜索树和代表点关系,得到增量后的聚类结果。
图1 TIOC-TWD算法流程
TIOC-TWD算法能同时解决增量聚类和重叠聚类问题,实验结果证明該算法的聚类准确率要高于其它增量重叠聚类算法。但TIOC-TWD算法在初始聚类时,将密度为1的点记为代表点,使算法在创建代表点搜索树及增量更新时浪费了大量时间。此外,算法在距离度量时并未考虑数据各属性重要度不同的问题,无法增强重要属性或消除冗余属性对聚类结果的影响,不能体现数据各属性之间的差异性,大大降低了聚类结果的准确率。
2 W-TIOC-TWD算法
针对TIOC-TWD算法不足,本文提出一种基于属性重要度的加权三支决策增量软聚类算法(W-TIOC-TWD算法),下面阐述算法定义及执行步骤。
2.1 基本概念及定义
定义1:代表点。如果条件|Neighbor(r)|≥ζ成立,ζ是密度阈值,就称 r为代表点,其代表了以r为中心、以δ为半径数据区域内所有数据对象。
定义2:代表区域。每个代表点 r 代表了以r为中心,以δ为半径的球形数据空间区域,将该球形区域作为代表点r的代表区域。
定义3:代表区域相似度。设D维数据空间中任意2个代表点分别为[ri]、[rj],则按照如下方式定义它们代表区域之间的相似性值大小。
[SimilarR(ri,rj)=Cover(ri)?Cover(rj)min(Cover(ri),Cover(ri))] (1)
式中,[Cover(ri)],[Cover(rj)]各自表示[ri]、[rj]代表区域数据对象的个数,[Cover(ri)?Cover(rj)]表示代表点[ri]、[rj]代表区域重叠部分中数据对象的个数。
定义4:数据元素相似性。算法中两个数据元素的相似性采用欧氏距离计算,计算公式如下:
[d(xi,xj)=k=1m(xi,k-xj,k)2] (2)
定义5:树节点。设代表点搜索树第i层第j个树节点为[Nodeij],[Nodeij]所包含的代表点集合为[{r1,r2,?,][rNodeij}]。[Nodeij]的值范围采用一个区间表示为[Nodeij=][[Nodeij.left,Nodeij.right]],其中,[Nodeij]左值和右值分別计算,即[Nodeij.left=min{ri1.left,?,riNodeij.left}],[Nodeij.right=][max{ri1.right,?,riNodeij.right}]。一个树节点由多个代表点组成,并且在第i维属性上组成树节点的代表点的数学值范围区间在树节点的值范围区间内。
定义6:数值范围相似性。设两个数值的范围代表区间分别为R1、R2,其代表区间的数据元素个数分别为[R1]、[R2],其中R1=[R1.left,R1.right],R2=[R2.left,R2.right],则当R1[?]R2[≠φ]时,称R1与R2这两个数值范围代表区间元素相似,即当R1[?]R2[≠φ]时认为两个数值范围是相似的。
定义7:数据非负标准化。在对数据集进行熵权重计算前,先对数据集进行非负标准化,将数据元素映射成[0,1]范围内的数据。
[rij=xij-min(xij)max(xij)-min(xij)] (3)
定义8:信息熵。属性j的信息熵[14]计算公式如下:
[Ej=-1lnni=1nbijlnbij] (4)
其中,[bij=riji=1nrij]。
定义9:熵权值。属性j的熵权值计算公式为:
[wj=1-Ejk=1m(1-Ek)] (5)
由公式(5)可知,信息熵越大,对应的属性熵权值越小,属性重要程度越低。
定义10:基于熵权值的加权距离。基于熵权值的加权距离计算公式如下:
[d(xi,xj)=k=1nwi2(xi,k-xj,k)2] (7)
其中[wi=1-Eik=1m(1-Ek)],m为属性个数。
定义11:离群点。假设数据集U在聚类之后,若聚类结果中存在不属于任何一个类簇且密度为1的代表点组成的类簇,则将此类簇定义为离群点并进行隔离。
2.2 W-TIOC-TWD算法
W-TIOC-TWD算法基本思想是:①通过对具有不同权重的各属性进行加权求和改进距离度量;②提出离群点这一概念,通过隔离离群点方法降低算法的时间复杂度。
W-TIOC-TWD算法由3部分组成:算法1为加权静态重叠聚类算法,算法2为创建代表点搜索树算法,算法3为增量更新算法。算法1的基本思想:首先对标准化处理的数据集进行属性权重计算,然后利用改进的距离计算公式寻找数据集的代表点,对数据集进行初始聚类,最后对初始聚类结果中的离群点进行隔离;算法2的主要任务是根据属性重要度创建代表点搜索树;算法3的基本思想是将增量数据与离群点结合,通过搜索树寻找增量数据集的邻居代表点,得到增量后的聚类结果。
图2简要展示了算法流程,其中红色虚线框内部分为W-TIOC-TWD算法与TIOC-TWD算法(图1所示)的改进之处。下面介绍W-TIOC-TWD算法中每个子算法实现。
2.2.1 加权静态重叠聚类算法(算法1)
针对TIOC-TWD中忽略属性重要度这一不足,提出一种加权静态重叠聚类算法(详见算法1)。首先,对标准化处理的数据集进行属性权重计算,为数据各属性分配权重。属性重要度分配能够起到强化重要属性消除冗余属性作用[13];然后,利用改进的距离计算公式寻找数据集代表点,对数据集进行初始聚类;最后,对初始聚类结果中的离群点进行隔离。
图2 W-TIOC-TWD算法流程
2.2.2 创建代表点搜索树算法(算法2)
树结构具有简单、快速、易查找和更新的特点,适合处理动态增量问题。搜索树的创建由属性重要度大小确定,采用自上向下的方式构建。本算法树结构节点由若干个代表点组成,每个树节点代表了这些代表点所处的数据空间区域。本文在建立搜索树时根据信息熵(公式4)确定属性优先程度,信息熵值越大其所对应属性的模糊程度越高,需要根据更多信息确定。
2.2.3 增量更新算法(算法3)
针对新到来的增量数据提出增量更新算法。该算法由3部分组成:①根据算法1中代表点的寻找方法寻找增量数据代表点;②利用算法2创建的代表点搜索树,寻找增量数据代表点的邻居代表点;③对发生变化的代表点及代表区域进行更新,即更新代表点搜索树和代表点关系图。
增量更新算法与原算法不同之处是,增量数据各属性的权重由初始数据集和增量数据集共同组成的数据集整体确定。
2.2.4 算法性能分析
为降低算法的时间复杂度,提高算法效率,本文提出离群点这一概念,下面介绍隔离离群点方法对算法性能的影响。
算法1是加权静态重叠聚类算法,设数据块大小为h,数据属性个数为m,代表点总数为|R|,则计算距离矩阵及寻找数据对象邻居所需时间为[O(n2)],根据邻居个数数据对象的排序时间为[O(nlog(n))]。假设代表点代表区域中的数据对象个数为p,则寻找代表点所需时间为[O(R*p*m+][nlog(n))],创建代表点关系图所需时间为[O(2*R2)]。通过计算发现,寻找代表点及创建代表点关系图的时间复杂度均与|R|的大小直接相关。由此可知,通过隔离离群点的方法可使|R|变小,从而降低寻找代表点及创建代表点关系图的时间复杂度。
Algorithm1:加权静态重叠聚类算法
Input:初始数据集[U],阈值[α,β,δ];权重[wi];
Output: 聚类结果集,R,Neighbor([ri]);
过程:
初始化R=[φ]、代表点邻居集合Neighbor([ri])=[φ]、类簇集合C=[φ] ;
根据式(5)计算数据集的属性权重值[wi];
利用公式(7)生成距離矩阵[Distance(x,y)];
计算每个数据元素的邻居数据Neighbor([xi]);
按照[Neigbor(xi)]值大小排序距离矩阵[Distance(x,y)]中[xi]所在的行;
将[Distance(x,y)]中第一行的数据对象(设为[x1])作为[rnew]的几何中心;
[cover(rnew)]中的每个元素[xi],删除距离矩阵[Distance(x,y)]中[xi]所在的行;
将新生成的代表点[rnew]添加到代表点集合R中,并从代表点集合中根据定义11进行离群点的隔离;
for(对于任意两个代表点[ri]);
根据公式(1)计算相似度并添加强弱连通边构建代表点无向关系图;
宽度优先搜索算法寻找代表点无向关系图中的强连通子图;
for (任意强连通子图[G]);
for (强联通子图中的每一个代表点[ri]);
[Pos(Cnew)=Pos(Cnew)∪Cover(ri)];
for (与强联通子图有弱边相连的每一个代表点[rj]);
[Bnd(Cnew)=Bnd(Cnew)∪Cover(rj)];
[Cnew= Pos(Cnew)∪Bnd(Cnew)];
最终的聚类结果C=C[?][Cnew];
算法2 为创建代表点搜索树算法,最坏情况下代表点搜索树一共有m层,每层需要对|R|个代表点进行排序,则需要进行[(R*(R-1))]次计算,从而分裂节点,所以算法2的时间复杂度为[O(m*(RlogR+R*(R-1))),]也与|R|的大小直接相关。
算法3是增量更新算法。假设离群点的个数为|r|,增量数据块有[R]个代表点,树节点共有L个子节点,查找新增代表点邻居代表点的时间复杂度为[O(m*(L*log(L)+][L+(R-|r|))]。假设每个代表点的代表区域有k1个数据对象,邻居代表点集合大小为k2,则算法3的时间复杂度为[O(|R|*(m*(L*log(L)+L)+R-|r|))]。通过计算可知,随着离群点个数|r|的增加,算法3的时间复杂度降低。
由于W-TIOC-TWD算法的3个子算法串行执行,所以该算法的时间复杂度为[O(sum(算法1,算法2,算法3))]。通过对3个子算法时间复杂度的分析可知,本文通过隔离离群点方法,分别降低了3个子算法的时间复杂度。所以,隔离离群点方法可以降低W-TIOC-TWD算法的总体时间复杂度,提高算法时间效率。
Algorithm2:创建代表点搜索树算法
Input:初始数据集U,代表点集合R
Output:代表点搜索树
过程:
根据公式(4)计算初始数据集U各属性的[Ej]值;
按照[Ej]由大到小的顺序对数据各属性进行排序;
对每个代表点的各维属性的属性值范围进行排序,按照代表点在第j维属性的左值由小到大对代表点排序,并依次计算代表点的值范围相似度。
采用降序排序后的数据集属性集合创建搜索树的每一层树节点,即属性重要度越高的属性越先用于构造树的节点。
3 实验结果分析
为了定性和定量评估W-TIOC-TWD算法性能,设计两组实验:第一组实验在人工数据集上对算法进行定性分析,验证W-TIOC-TWD算法是否具有在增量数据下的类簇合并、增长以及发现新类簇等能力;第二组实验基于UCI[15]真实数据集进行定量分析,以准确率(Accuracy)作为评价指标,以最新、效果最好的增量软聚类算法TIOC-TWD算法和增量聚类算法OFCMD算法[16]作为比较算法。
Algorithm3:增量更新算法
Input:①增量数据集代表点集合R;②代表点无向关系图G;③参数[α、β、δ];
Output:聚类结果C={[C1],…[Ci],…[Cn]}
过程:
for (对任意增量数据代表点[rwait] )
FindNeighbor([rwait]);//寻找代表点[rwait]的邻居代表点
//Mapping each [xi] in [rwait] to neighbor representative points in[Rneighbor]
for ([rwait]代表区域中的任意一个[xi])
for ([rwait]中的任意代表点[ri])
根据公式(7)计算[xi]与[ri]之间的距离;
if (distance([xi],centriod [ri])[≤][δ])
Cover([ri])=Cover([ri])[?][xi];
if(there exists [xi] which cant map to any[ Rneighbor])
for([Rneighbor]中的任意代表点[ri])
for (代表点 [ri] 中的任意 [xj] )
if distance([xj],centriod[ rwait])[≤][δ]
Cover([rwait])=Cover([rwait])[?][xj];
add [rwait] to [ Rneighbor]
else
for(对于每一个树节点 [nodeij] in Path)
从树节点 [nodeij] 中寻找代表点[rwait],并将其从[nodeij] 中删除掉;
更新发生变化的代表点无向关系图G
for (each representative point [ri] in[ Rneighbor])
for(each representative point [ri] in neighbor([ri]))
根据公式(1)计算[ri]、[rj]代表区域的相似性,构建无向连通图;
new=0
for( each changed sub-graph [G'] in G)
new=+1;
for (each representative point [ri] in [G'])
POS([Cnew])=POS([Cnew])[?]Cover([ri]);
for(each [rj] which is linked to [G] with weak edge)
BND([Cnew])=BND([Cnew])[?]Cover([rj]);
C=C[?][Cnew];
3.1 数据与预处理
本文实验数据集为3个人工数据集和6个UCI真实数据集,数据集规模如表1所示。
第一组实验所用到的人工数据集D1、D2、D3是在二维坐标下随机生成的,维度即属性个数,且每组数据都属于一个类,其余6个数据集为第二组实验所用的真实数据集。letterABC和LetterAGI均为数据集Letter的一部分,letter ABC包括字母类A、B和C三个类标签,letter AGI包括字母A、G和I三个类标签;pendigits1234和pendigits1469均来自数据集 pendigits,pendigits1234包括1、2、3和4四个类标签,pendigits1469包括数字类1、4、6和9四个类标签。实验参数有3个,其中δ为距离阈值、α和β为连通边强弱阈值。
表1 数据集
3.2 实验设置
第一组实验,随机选择D2数据集80%的数据以及D1全部数据作为初始数据集,D2剩余20%数据作为增量数据,验证本文算法的类簇增长功能;随机选取D1数据集80%作为初始数据集,20%作为增量数据集,验证本文算法具有类簇合并功能;选取D3作为初始数据集,D1作为增量数据集验证本文算法具有发现新类簇功能。
第一组实验参数以0.1的间隔对参数进行插值调整,参数取值范围为[0,1],实验参数δ、α、β分别设置为0.35、0.25、0.01。
第二组实验将每个真实数据集划分为初始训练数据集和增量数据集两个部分。随机选取真实数据集60%数据作为初始训练数据集,剩余40%的数据分别均分为4组和2组,模拟连续4次每次10%的数据增量实验,以及连续2次每次20%的数据增量实验,具体增量数据流如图3和图4所示。
图3 连续4次10%增量数据流
图4 连续两次20%增量数据流
第二组实验参数采用0.1为间隔的插值分析方法进行调整,参数的取值范围[0,1],W-TIOC-TWD算法采用δ、α、β 三个参数最优值,见表2。
3.3 评价指标
在第二组定量实验中,用准确率作为评价指标对比本文算法与比较算法的性能。
定义12 准确率(Accuracy):设样本集X包括k个类,准确率计算公式如下:
[Accuracy=i=1kaiX] (8)
其中,[ai]表示被正确聚类到类[Ci]中的对象数,[X]表示集合中包含的元素数。
表2 参数最优值
3.4 实验结果及分析
3.4.1 人工数据集实验结果及分析
增量数据到来时,本文算法对类簇增长、合并、发现新类簇等处理能力实验结果如图5-图7所示。
由图5和图6可知,类2的数据个数随着增量数据的到来而增长。由图7和图8可知,随着增量数据的到来,类1和类2的边界域数据个数超过一定量时,两个类合并成一个类。由图9和图10可知,增量数据到来时,算法能够识别出新产生的类2。
结论1:通过在人工数据集的实验可知,当增量数据集到来时,W-TIOC-TWD算法具有使类簇增长、类簇合并和发现新类簇的能力。
图5 初始聚类结果一 图6 增量聚类结果一
图7 初始聚类结果二 圖8 增量聚类结果二
图9 初始聚类结果三 图10 增量聚类结果三
3.4.2 UCI数据集实验结果及分析
基于UCI[15]真实数据集上的横向定量比较实验结果如表3、表4所示。
表3 增量数据为10%时对比试验结果
表4 增量数据为20%时对比试验结果
由表3可知,在增量数据为10%时,W-TIOC-TWD算法在LetterABC、LetterAGI、 Pendigists1469数据集上的聚类准确率比TIOC-TWD算法和OFCMD算法有明显提高,其余3个数据集上的准确率也和最高值相差无几。
由表4可知,在增量数据为20%时,W-TIOC-TWD算法在数据集LetterABC、LetterAGI、Banknote、Pendigists1469上的聚类准确率比其余算法要高,而在数据集Waveform、Pendigists1234上,本文算法准确率也与最高值相差无几。
通过增量占比为40%,模拟连续4次10%以及两次20%的增量聚类实验结果可知,将各属性的重要程度以加权方式体现在距离度量计算中,可以有效加强重要属性对聚类结果的积极影响,消除冗余属性对聚类结果的消极影响,从而提高聚类准确率,由此验证了本文算法的有效性。
结论2:通过在UCI真实数据集的实验可知,在增量数据为10%和20%时,本文W-TIOC-TWD算法在聚类准确率上要优于其余两种算法。通过本文算法与其余两种算法实验对比,证明了本文提出的加权距离公式有效解决了数据各属性重要程度不同的问题,验证了本文所提出的距离加权公式的有效性。
4 结语
在分析增量聚类以及软聚类算法研究现状基础上,为降低现有算法的时间复杂度,解决现有算法未考虑数据各属性重要度这一问题,提出一种加权三支决策增量软聚类算法(W-TIOC-TWD)。该算法将属性重要度考虑到距离度量公式中,给出一种基于属性重要度的加权距离度量方法。将各属性重要度的不同体现在算法中,并提出离群点这一概念。利用隔离离群点的方法降低算法的时间复杂度,并从算法的角度分析这一行为的有效性。通过在人工数据集实验可知,W-TIOC-TWD算法具有使类簇增长、合并以及发现新类簇的功能。通过UCI真实数据集上实验,证明本文算法在聚类准确率上优于其余两种算法,证明W-TIOC-TWD算法的有效性。
虽然本文在一定程度上提高了聚类性能,但仍有很多方面值得进一步研究:①本文所提算法中涉及到的参数,均是通过插值法选取最优参数,在接下来的工作中,可以考虑采用贝叶斯理论、层次分析法、优化算法、博弈论、统计学等方法解决最优参数选择问题;②考虑到当下数据具有格式多样、结构复杂、数量庞大、实时更新等特点,进一步提高本文算法的普适性尤为重要;③本文算法利用三支决策的思想对数据进行聚类,但未将算法应用到实际推荐系统中,下一步研究可考虑将W-TIOC-TWD算法应用到包含增量和重叠数据的推荐系统中。
参考文献:
[1] 海沫. 大数据聚类算法综述[J]. 计算机科学,2016,43(S1):380-383.
[2] YU H, ZHANG C, WANG G. A Tree-based incremental overlapping clustering method using the three-way decision theory[J]. Knowledge-Based Systems,2016, 91(C) :189-203.
[3] SANJAY CHARKRABORTH,NAGWANI N K. Analysis and study of incremental k-means clustering algorithm[J]. High Performance Architecture and Grid Computing, 2011(169): 338-341.
[4] PHAM D T,DIMOV S S,NGUYEN C D. An incremental k-means algorithm[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989-1996 (vols 203-210), 2004, 218(7):783-795.
[5] ALM S,KUMAR K R S. A density based dynamic data clustering algorithm based on incremental dataset[J]. Journal of Computer Science,2012,(5):656-664.
[6] 刘青宝,侯东风,邓苏,等. 基于相对密度的增量式聚类算法[J]. 国防科技大学学报, 2006,28(5):73-79.
[7] LEI G,YU X,YANG X,et al. An incremental clustering algorithm based on grid[C]. Fuzzy Systems and Knowledge Discovery (FSKD),2011 Eighth International Conference on,2011:1099-1103.
[8] 刘卓,杨悦,张健沛,等. 不确定度模型下数据流自适应网格密度聚类算法[J]. 计算机研究与发展,2014, 51(11):218-221.
[9] LABROCHE N. Online fuzzy medoid based clustering algorithms[J]. Neurocomputing,2014(126): 141-150.
[10] PETERS G,WEBER R,NOWATZKE R. Dynamic rough clustering and its applications[J]. Applied Soft Computing,2012,12(10): 3193-3207.
[11] PéREZ-SUáREZ A,MARTíNEZ-TRINIDAD J F,CARRASCO- OCHOA J A,et al. An algorithm based on density and compactness for dynamic overlapping clustering[J]. Pattern Recognition, 2013,46(11): 3040-3055.
[12] YAO Y Y. The superiority of three-way decisions in probabilistic rough set models[J]. Information Sciences,2011,181(6):1080-1096.
[13] 于洪,毛传凯. 基于k-means的自动三支决策聚类方法[J]. 计算机应用,2016,36(8): 2061-2065.
[14] BARBARá D,LI Y,COUTO J. Coolcat: an entropy-based algorithm for categorical clustering[J]. Giteseerx, 2002,1(4):582-589.
[15] LABROCHE N. Online fuzzy medoid based clustering algorithms[J]. Neurocomputing,2014(126):141-155.
[16] 周漩,張凤鸣,惠晓滨,等. 基于信息熵的专家聚类赋权方法[J]. 控制与决策,2011,26(1):153-156.
[17] KOHAVI?R,?BECKER B.Machine learning repository[EB/OL]. [2014-11-16]. http:// archive.ics.uci. edu/ ml/.
(责任编辑:杜能钢)

