基于数据驱动的超导临界温度预测方法研究
李韬伟 王龙 赵宸立

摘 要:超导体具有零电阻特性、完全抗磁性、通量量子化等优点,但受限于物理实验环境与材料自身特性,其临界温度测试一直是超导实验中的难点。对公开超导数据集进行研究分析,以期发现其临界温度与物理特性及化学元素组成之间的关系,进而构建能够辅助预测超导体临界温度的模型,降低实测获得临界温度的难度。结合数据挖掘领域的相关性分析与多元线性回归分析等理论,分别基于超导临界温度实验的物理属性数据及元素构成数据构建预测模型,为通过数据驱动实验获取其它超导体临界温度提供了有益尝试。通过对两个模型进行对比,结果表明,基于元素的预测模型效果略优于基于属性的预测模型。
关键词:超导体数据集;数据驱动;相关性分析;多元线性拟合
DOI:10. 11907/rjdk. 182872 开放科学(资源服务)标识码(OSID):
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2019)008-0029-04
A Data-driven Research on Critical Temperature Prediction of Superconductors
LI Tao-wei1, WANG Long1, ZHAO Chen-li2
(1. National University of Defense Technology,Wuhan 450001,China;2. Unity of 32023 of PLA,Dalian 116000,China)
Abstract: The superconductor has the advantages of zero resistance, complete diamagnetism, flux quantization and the like. Because of the critical temperature test and the material's own characteristics, its critical temperature test has always been a difficult point in superconducting experiments. In this paper, we study and analyze the open superconductor dataset in CUI, and try to find the relationship between its critical temperature and its physical properties and chemical element composition. Then we can construct a model that can help predict the critical temperature of superconductors. Combining the correlation analysis and multiple linear regression analysis theory in the field of data mining, this paper separately predicts the model based on attribute data and element data, and provides a useful attempt for data-driven experiments to obtain the TC of superconductors. The results show that element-based model effect is better than the that of attribute-based model.
Key Words: superconductor data dataset; data-driven; correlation analysis; multiple linear regression analysis
基金項目:教育部联合基金项目(6141A02011607)
作者简介:李韬伟(1990-),男,国防科技大学信息通信学院助教,研究方向为数据挖掘、数据分析、虚拟现实。
0 引言
超导体(Superconductor)是指一种电阻在某一温度下为零的导体,具有零电阻特性、完全抗磁性、通量量子化的特点。超导体的零电阻特性与外界环境的磁场及温度紧密相关,很容易受到温度场和磁场变化影响而被破坏;完全抗磁性则与材料本身属性相关,是指在磁场中磁力线无法穿过导体的现象;通量量子化则是当两个超导体之间的绝缘层薄至原子尺寸时,电子对可以穿过绝缘层产生隧道电流的现象。
超导体临界温度测量一直以来都是超导实验中的难点[1]。游彪等[2]通过测量加热过程中超导体电阻变化记录其临界温度,需要考虑样品与铜底座接触率、恒温器热平衡状态等,难度较大;赵林等[3]从不同体系铁基超导体电子结构的角分辨率电子能谱角度,提出铁基超导新理论,为解决高温超导机理问题提供了依据;殷培环[4]研究了钡元素掺杂用Pb对Bi位替代得到的超导体临界温度变化;吴平[5]也利用电阻—温度特性测量钇钡铜氧超导材料的临界温度。通过常用物理手段测量超导温度,对精密测量仪器、实验员经验及实验环境等要求非常严格,往往需要耗费大量人力、物力才能获取近似测量值。
近年来,随着大数据、人工智能等数据技术的发展,基于数据驱动的方法越来越广泛地被应用于各个领域。杨丽洁[6]利用卫星采集数据与模拟水文及气候,成功实现了洪水预报;聂虹等[7]通过分析地质、物探、化探、遥感等数据,构建矿产预测模型。数据驱动方法的特点为:①建模方法具有一般通用流程;②模型固定效果好,模型主要集中于几个常用类别,如VM[8]、决策树[9]、深度学习[10]等,适用于绝大多数应用场合;③数据预处理过程简单,相比于传统方法,需要领域专家介入的环节较少。
本文拟采用数据驱动方法,在已知数据集的前提下,抽取数据集属性特征,通过机器学习方法训练相应模型,得到一种基于数据的超导体临界温度预测方法,进而通过超导化合物的化学元素即能给出相应超导体临界温度。
1 数据集
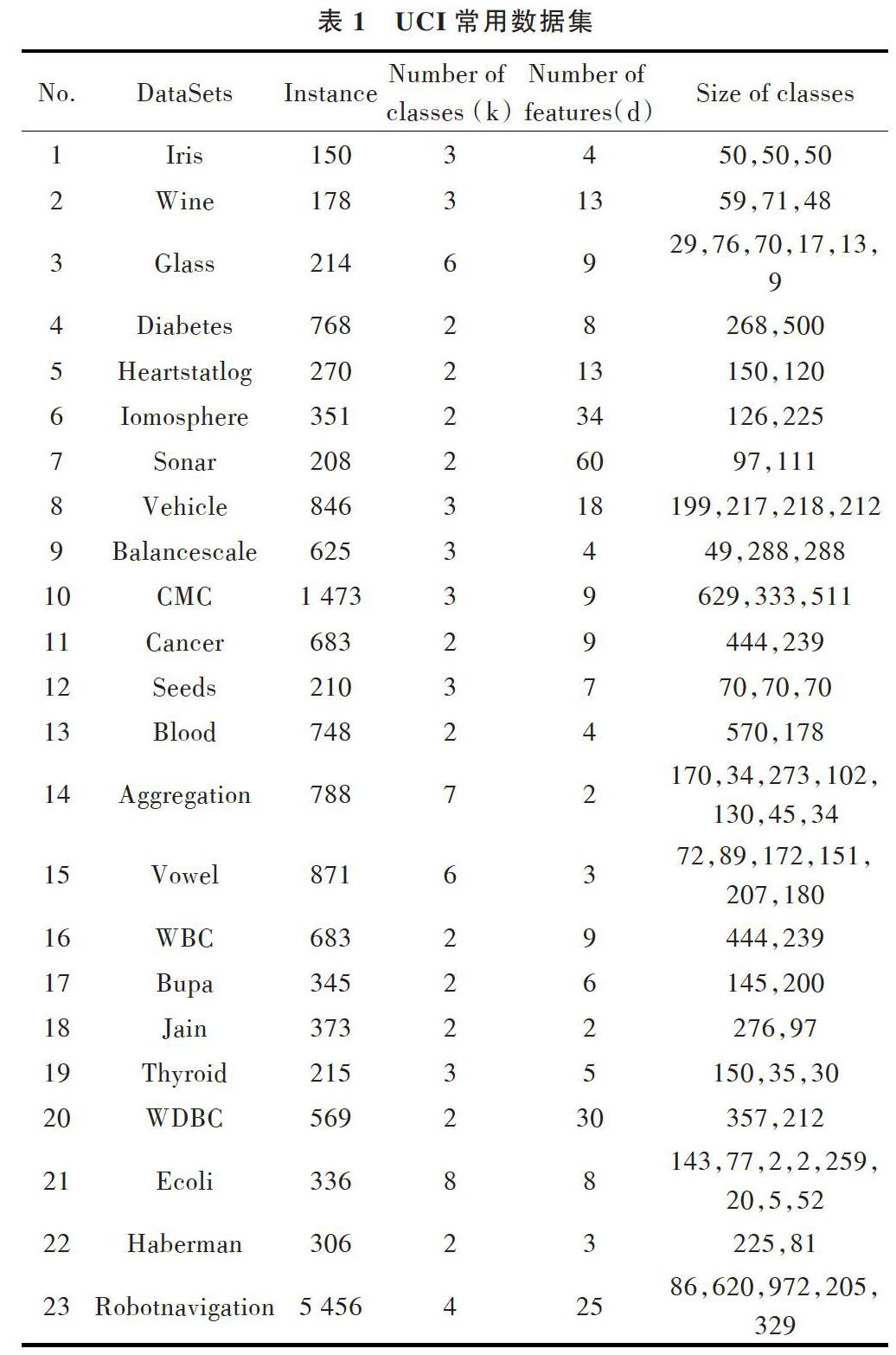
2018年10月12日,UCI[11]数据库更新了一份超导数据集。UCI数据库是加州大学欧文分校(University of CaliforniaIrvine)提出的用于机器学习的数据库,该数据库的数据集一直在不断增加。该机构是比较权威的数据发布机构,表1列出了常用数据集。
表1 UCI常用数据集
UCI提供的超导数据集(Superconductor Data Dataset)中详细记录了已知21 263种超导体的临界温度,其中train.csv列举了从21 263种超导体中提取的81个特征及临界温度;unique_m.csv列出21 263种超导体的化学式及其临界温度,主要列出了每种超导体中包含的86种化学元素及摩尔质量。例如第一种超导体Ba0.2La1.8Cu1O4中包含4种化学元素,其摩尔质量分别为Ba 0.2、La 1.8、Cu 1、O 4。
将数据分成两类,一类作为训练集,用于学习预测超导体临界温度的模型参数,占数据量的70%,剩下的30%作为测试集,用于检测模型效果。
2 超导数据集分析
目前对超导体临界温度的研究有针对其特有元素类型进行的相关测试研究,如对铁系超导体技术的研究,还有针对元素组成的测试研究[3-5,13,14],以及针对η-配对超导体临界温度的研究等[15]。本文通过对数据集中超导体化学元素的分析,旨在找到其临界温度与化学式元素的关系,以此预测超导体临界温度。
2.1 超导体属性数据分析
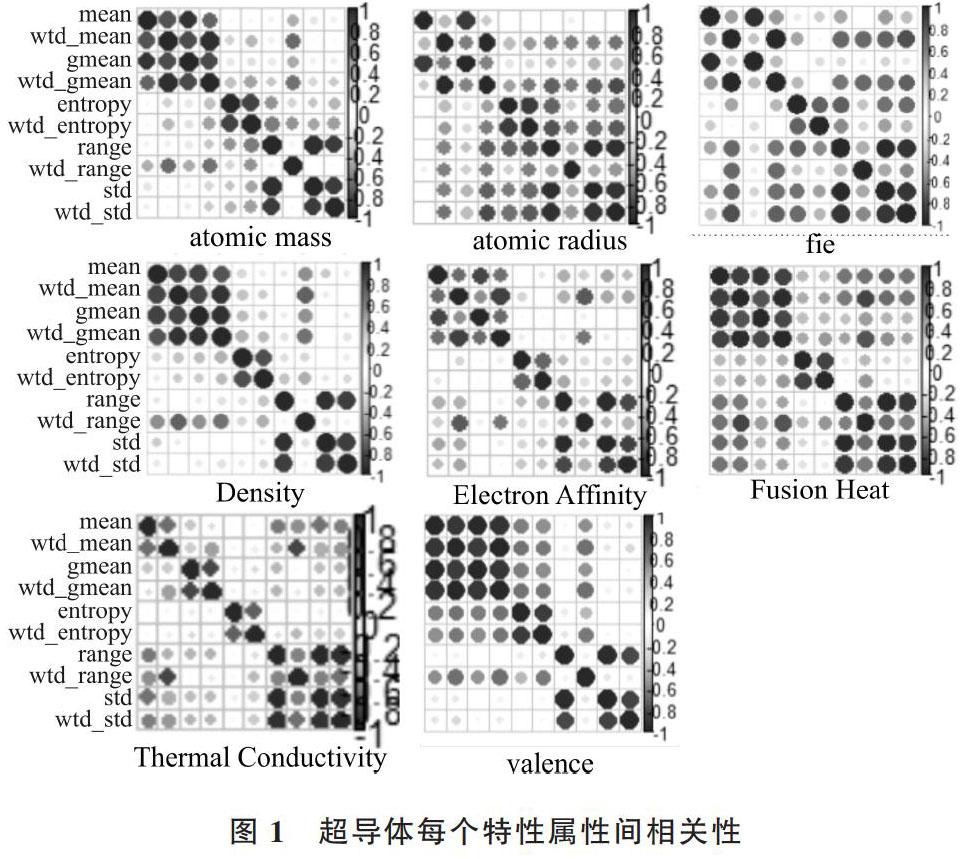
超导体特性中,除元素数量外,其它几个特性相互之间影响较大,需要先进行相关性分析与主成分分析[16]。利用R语言分析属性数据中每个特性下10个属性的相关度,如图1所示。
图1 超导体每个特性属性间相关性
如图1所示,每种特性中,前4个属性(mean, wtd_mean, gmean, wtd_gmean)相关性较高,5、6两个属性(entropy,wtd_entropy)相关性较高,最后两个属性(std_rang,wtd_std_rang)相关性较高。据此确定特性选择方案,在每个特性中选择mean、entropy和std_rang 3个属性作为特征。
对特性数据集进行处理后,利用R语言采用多元线性回归方式建立学习模型, 多元线性回归相关理论可参考文献[17-23],最后得到各元素回归系数如表2所示。
表2中回归系数代表超导体中该属性大小对临界温度的作用,大于0表示起正向作用,属性值越大,超导体临界温度越高;小于 0表示起负向作用,属性值越大,超导体临界温度越低。
表2 基于属性数据的多元线性模型回归系数
将该模型与属性数据测试集中结果进行对比,对比结果如表3、表4所示。
表3 属性数据模型预测结果(部分)
表4 属性数据模型测试结果统计
[温度相差范围\&超导体数量\&10华氏度以内\&2 380\&20华氏度以内\&1 768\&30华氏度以内\&751\&40华氏度以内\&283\&50华氏度以上\&130\&]
对于测试集中的6 379種超导体,对其临界温度预测效果较好(误差在10华氏度以内)的只有2 380种,占比为37.3%,还需要对算法作进一步改进。
2.2 超导体元素数据分析
由化学元素组成的化合物,在稳定形态下各元素都有固定化学键,取正价的元素键之和必须等于取负价的元素键之和。因此,分析各元素之间的相关性是十分必要的。对数据集中86个元素组成化合物的相关性进行分析,结果如图2所示。
图2 元素相关性分析结果
由图2可知,每个元素除与自身有强关联性外,与其它元素的相关性不高。具体而言,相关系数高于0.5的元素对有7组,如表5所示。
表5 高相关性元素对
86种元素中,涉及元素相关性较高(大于0.5)的只有7对14种元素,而数据集的21 263种超导体材料中,除氧O和铜Cu等常见元素外,其它高相关性的超导体只有 3 189种,占总数量的15%。高相关性(大于0.8)元素对只有铁元素Fe与砷元素As,同时包含铁砷的化合物有1 374种,占比为6.5%。关于铁砷元素的超导体研究方法可参考陈宁、刘洋等[13]的研究内容。
针对高关联性元素占比较少的特点,对元素数据集同样采用多元线性回归方式建立学习模型,得到各元素回归系数如表6所示。
表6中元素项对应的回归系数代表超导体中该元素含量对临界温度的作用,大于0表示起正向作用,含有该元素越多,超导体临界温度越高;小于 0表示起负向作用,含有该元素越少,超导体临界温度越低;等于0表示不起作用,共有10种元素的回归系数为0,分别是稀有气体惰性元素氦He、氖Ne、氩Ar、氪Kr、氙Xe、氡Rn,以及稀土元素钷Pm,稀有元素钋Po和砹At,数据集中的超导体都不包含这些元素。例如,第3种化合物为Ba0.1La1.9 Cu1O4,临界温度为19,利用该模型预测的临界温度计算方式为:
[14.481 92+0.1×23.973 66+1.9×(-0.087 78)+1×0.463 187+4×(-0.362 83)=15.72]
预测结果与真实临界温度相差不超过4华氏度。
表6 基于元素数据的多元线性模型回归系数
将该模型与测试集中数据进行对比,对比结果如表7、表8所示。
表7 元素数据模型预测结果(部分)
表8 元素数据模型测试结果统计
[温度相差范围\&超导体数量\&10华氏度以内\&2 632\&20华氏度以内\&1 926\&30华氏度以内\&1 006\&40华氏度以内\&473\&50华氏度以上\&274\&]
对于测试集中的6 379种超导体,对临界温度预测较准确(误差在10华氏度以内)的只有2 632种,占比为41.3%,差距超过100华氏度的有14种。虽然结果相比属性数据模型略优,但该模型仍需要作进一步改进。
3 结语
本文以超导体数据集为基础研究影响其临界温度的属性及元素组成,为条件严苛的物理实验提供了数据驱动的分析视角。实验结果表明,基于元素的模型预测结果略优于基于属性的元素模型预测结果。在后续研究中将尝试根据属性取值与元素质量分段建立模型,研究相关性较强的部分超导体的特殊性,并分析临界温度与实测临界温度差距超过100华氏度的具体原因。
参考文献:
[1] 胡殿才,段旭如,夏元良. 超导体临界温度的测量[J].大连理工大学学报,1988(3):113-116.
[2] 游彪,吴卫国,吴小山. 综合研究性实验试题:高温超导体特性测量综合实验[J]. 物理实验, 2018, 38(10):36-39.
[3] 赵林,刘国东,周兴江. 铁基高温超导体电子结构的角分辨光电子能谱研究[J]. 物理学报,2018,67(20):246-271.
[4] 殷培环. Ba位掺杂对BaPb_(0.77)Bi_(0.23)O_(3-δ)超导电性的影响[D]. 南京:南京大学,2018.
[5] 吴平. 高T_c超导材料YBCO临界温度测量方法[J]. 大学物理实验,2006(3):5-7.
[6] 杨丽洁. 数据驱动模型在洪水预报中的应用及其发展趋势[J]. 电脑知识与技术,2018,14(17):275-277.
[7] 聂虹,朱月琴,常力恒,等. 数据驱动下的矿产预测模型构建方法研究[J]. 中国矿业,2018,27(9):82-87.
[8] CORTES C,VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3):273-297.
[9] QUINLAN J R. Induction of decision trees[J]. Machine Learning, 1986 (1):81-106.
[10] HINTON G. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2010, 9(1):926-947.
[11] UCI Machine Learning Repository. UCI数据集[EB/OL]. http://archive.ics.uci.edu/ml/index.php.
[12] 师瑞华. BP神经网络在粮仓平均温度预测中的应用[J]. 软件导刊,2015,14 (8): 42-44.
[13] 陈宁,刘洋,贾亚魁,等. FeAs超导体临界温度的键长和半径效应[J]. 中国科学,2009(9): 1295-1299.
[14] HAMIDIEH K. A data-driven statistical model for predicting the critical temperature of a superconductor[J]. Computational Materials Science, 2018, 154:346-354.
[15] 王志君,邱孝明,肖业高. η-配对超导体的临界温度[J].低温物理学报, 1994(6):462-467.
[16] 赵蔷.主成分分析方法综述[J].软件工程,2016,19(6):1-3.
[17] 纪钦洪,孙洋洲,于航,等. 基于多元线性回归的碳配额价格预测模型研究[J].现代化工,2018,38(4):220-224.
[18] 陈崇双,唐家银,何平. 方差分析法的线性回归建模重构[J]. 统计与决策,2018(7):71-75.
[19] 李金海. 多元回归分析在预测中的应用[J]. 河北工业大学学报, 1996(3):57-61.
[20] 郭会利. 多元回归分析的逐步回归预测模型[J]. 考试周刊, 2009(26):92-93.
[21] 王惠文,孟洁. 多元线性回归的预测建模方法[J]. 北京航空航天大学学报, 2007, 33(4):500-504.
[22] 胡泽文,武夷山. 科技产出影响因素分析与预测研究——基于多元回归和BP神经网络的途径[J]. 科学学研究,2012,30(7):992-1004.
[23] 张洪祥,毛志忠. 基于提取综合特征因素的投影寻踪多元线性回歸分析[J]. 统计与决策,2010(24):31-34.
(责任编辑:黄 健)

