空中非合作目标旋转部件位置估计方法*
高 磊,曾勇虎,汪连栋,王 伟
(1. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003;2. 中山大学 电子与通信工程学院, 广东 广州 510006)
逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)观测的目标通常都是非合作目标。当使用ISAR观测空中非合作目标时,如果存在旋转部件,按照常规方式开展成像处理时,旋转部件对信号的调制作用会导致成像质量的下降[1-4],从而降低后续散射特征提取与识别结果准确性。
在存在旋转部件的情况下,为了提高ISAR图像质量,常见的处理思路是从高分辨距离像(High Resolution Range Profile, HRRP)数据中分离出旋转部件对应的微动分量,文献[5-9]分别按照不同的方式实现了这个目标。在实现旋转部件对应的微动分量分离过程中,一个重要的前提是确定微动分量在HRRP中的位置。
文献[1]使用经验模态分解(Empirical-Mode Decomposition, EMD)得到的固有模式函数(Intrinsic-Mode Function, IMF)分量中的零点个数来估计旋转部件位置,文献[10]则根据径向距离单元熵值的大小来确定旋转部件位置。文献[1]的做法需要对全部距离单元进行EMD运算,计算量较大;而文献[10]中根据熵值大小估计位置的原则不够稳健,如果存在散射幅度强的非旋转部件,则也会被认为是旋转部件。
基于上述情况,在分析旋转部件在ISAR图像中分布特点基础上,本文提出基于方位向距离单元熵和局部径向距离单元熵的旋转部件位置估计方法。
1 包含旋转部件的宽带成像特点分析
光学区条件下,目标一般都满足散射点模型假设,即雷达回波可等效为一系列散射点回波的叠加。下面建立包含旋转部件目标的散射点回波模型。
实际ISAR在对空中目标进行成像时,目标相对于雷达的运动可以分解为两部分:径向运动和切向运动。径向运动是指目标沿着雷达波照射方向的运动,切向运动是指目标垂直于雷达波照射方向的运动。径向运动不利于方位向散射点的高分辨,故在成像处理中需要通过运动补偿的方式,补偿径向运动,仅保留目标的切向运动,进而将一般运动目标转化成转台运动目标[11]。为简化分析,这里直接考虑转台目标的成像观测模型。为描述目标相对雷达的运动情况,建立雷达坐标系T-UV、目标坐标系O-XY和局部坐标系o-ξη,如图1所示。假设目标由主体部分和微动部分组成,不失一般性,可设微动部件运动为旋转运动。在成像期间,目标主体以角速度ω0绕转动中心O匀速转动,旋转部件在伴随主体运动的同时,还以角速度ω1绕其自身转动中心o做高速旋转。

图1 含旋转部件目标的成像观测模型Fig.1 Imaging observation geometry model for target with rotating part
设雷达发射宽带线性调频信号为:
(1)


(2)

注意到,第二个求和符号中,旋转部件散射点位置随慢时间的变化规律不再是线性变化,与主体散射点相比,多了一个余弦函数。
对比式(2)中主体散射点与旋转部件散射点位置随慢时间变化的规律可知:
1)主体散射点位置随慢时间变化呈现出线性变化,在旋转部件散射强度不是特别强的前提下,经过包络对齐之后,主体散射点在不同慢时间HRRP中的位置被对准,进而,在处理多帧HRRP进行方位向分辨得到ISAR图像时,能够实现良好聚焦。
2)旋转部件散射点位置随慢时间变化呈现线性变化叠加正弦变化,经过包络对齐之后,旋转部件散射点在相邻HRRP中的位置无法对准。设信号分辨率为Δr,上述旋转部件散射点在不同慢时间HRRP中的位置会在⎣2rq/Δr」个距离单元范围内振动。进而,在处理多帧HRRP进行方位向分辨得到ISAR图像时,对于存在旋转部件的距离单元,沿着方位向会呈现严重散焦,即在ISAR图像中,存在一个或多个径向距离单元沿方位向呈现条带状散射结构分布。
2 旋转部件位置估计方法
结合前一部分对主体散射点和旋转部件散射点在ISAR图像中表现特点的分析结果,本部分在径向距离单元熵的基础上,定义方位向距离单元熵和局部径向距离单元熵,进而提出旋转部件位置估计方法。
文献[10]定义的径向距离单元熵如下:设ISAR图像矩阵为g(k,n),k(k=1,2,…,K)表示方位向距离单元序号,n(n=1,2,…,N)表示径向距离单元序号,则径向距离单元熵ε(n)为:
(3)
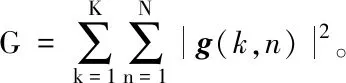
下面给出方位向距离单元熵和局部径向距离单元熵的定义。
定义1方位向距离单元熵εC(k)为:
(4)
式(4)反映了ISAR图像中对应每个方位向距离单元上的能量与整体能量的加权比值。
式(3)和式(4)的形式具有相似性,但其含义是不同的,图2直观地给出了这两个公式的含义对比。在K×N维ISAR图像矩阵中,式(3)对应的是矩阵中第n列元素在整体图像能量中的加权比值,而式(4)对应的是矩阵中第k行元素在整体图像能量中的加权比值。ISAR图像中的行序号和列序号具有不同含义,行序号对应方位向距离单元序号,而列序号对应径向距离单元序号,因此式(3)和式(4)实际上是从两个角度说明ISAR图像中的能量分布情况的。

图2 两种距离单元熵含义对比Fig.2 Comparison of two range cell entropy
定义2设Γ为ISAR图像矩阵g(k,n)中按照一定规则确定的部分行序号集合(即部分方位向距离单元序号集合),则局部径向距离单元熵为:
(5)

旋转部件在HRRP中的位置估计方法步骤如下:
Step1:对ISAR图像数据按照式(4)计算方位向距离单元熵εC(k);
Step2:找出方位向距离单元序号kmax,使得εC(kmax)=max(εC(k));


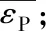

备注1:kmax通常在⎣K/2」附近,如果存在极端情况,则考虑按照循环移位的方式在1,2,…,K范围内确定kmax前后⎣K/W」区间作为目标区域。
备注2:Λ为预先设定值,如果成像结果中噪声较强,则经验取值为5~8;如果成像结果中噪声很弱,则经验取值为10~20。
上述估计方法的内在物理意义有两点:第一,沿着方位向,计算每个距离单元上的能量与整体能量的加权比值,以最大值前后⎣K/W」区间作为目标区域;第二,在存在旋转部件情况下,在目标主体区域之外的部分,旋转部件对应的径向距离单元能量应该远高于其余的径向距离单元。
通过上述处理,可以实现ISAR图像中旋转部件位置的自动估计,进而能够支撑从HRRP中分离旋转部件信号分量,以提升目标主体部分ISAR图像质量。
3 数据验证与性能分析
3.1 仿真数据验证
通过仿真实验,对上述方法进行验证。仿真验证设置如下:
1)目标模型:主体散射结构是由44个散射点组成的飞机状散射点模型,如图3所示(图中坐标轴对应目标坐标系)。主体散射结构散射点强度设置为3~8之间不等,但将机身中间位置个别散射点的强度设置为12。在上述模型中,设置两个旋转部件,位于机翼两侧,如图3中用五角星标出的位置。两个旋转部件的转动参数相同:旋转半径为0.2 m,旋转周期20 r/s。两个旋转部件散射点强度设置为11。

图3 仿真目标散射点模型Fig.3 Scatter model of target for simulation
2)观测位置:雷达坐标系与目标坐标系的坐标轴平行,目标坐标系原点在雷达坐标系中的坐标是(8000 m,8000 m),目标坐标系在雷达坐标系中的X轴方向速度为-230 m/s,Y轴方向速度为-50 m/s。
3)雷达参数:载频为10 GHz;带宽为1 GHz;脉宽为50 μs;宽带信号脉冲重复频率为500 Hz。
在上述参数设置下,成像观测时间为1 s,对500帧宽带雷达回波进行成像处理,其ISAR图像结果和径向距离单元熵结果如图4所示。
在图4(a)中,由于旋转部件的存在,使得在ISAR图像中,沿着方位向,出现两个明显的散射条带,这就是旋转部件存在的距离单元范围。对比图3和图4(a)可知,ISAR图像中旋转部件的位置分布与目标模型中旋转部件的位置设定是一致的。具体来说,在ISAR图像结果中,存在旋转部件的径向距离单元序号是300,340。而由图4(b)可知,其径向距离单元熵最大的距离单元序号为320,并不在图4(a)ISAR图像提示的旋转部件距离单元范围内。

(a) 仿真数据ISAR图像(a) ISAR image of simulation data

(b) 径向距离单元熵(b) Range cell entropy图4 飞机模型仿真数据ISAR图像与径向距离单元熵Fig.4 ISAR image of simulation data for airplane model and its range cell entropy
按照第2节的方法对旋转部件进行位置估计。相应的方位向距离单元熵和局部径向距离单元熵结果如图5所示。根据图5(a)的结果确定目标主体部分的位置后,对ISAR图像余下的部分进行计算,得到图5(b)的结果。
从图5(b)中的局部径向距离单元熵计算结果可知,旋转部件对应的位置分别是:序号300和340附近的距离单元,这与ISAR图像结果以及仿真设置是相同的,从而验证了所提方法的有效性。在仿真数据中未叠加噪声,故在进行旋转部件位置估计时,门限设定为熵均值的20倍,即Λ=20。

(a) 方位向距离单元熵(a) Cross range cell entropy
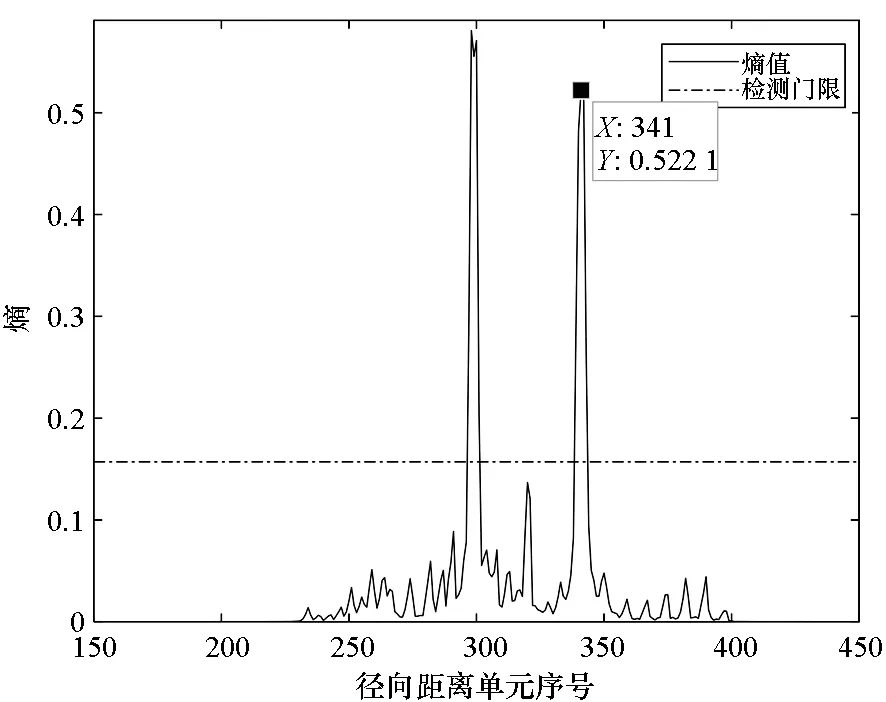
(b) 局部径向距离单元熵(b) Local range cell entropy图5 位置估计过程中得到的两种熵计算结果Fig.5 Result of two kinds entropy in position estimation
3.2 实测数据验证
进一步应用某飞机目标宽带雷达实测数据进行验证。通过观察其ISAR图像结果可知,存在显著的旋转部件。处理该目标实测数据的500帧回波数据得到的ISAR图像以及径向距离单元熵如图6所示。图6(a)中两条沿方位向的不均匀条带即为旋转部件导致的方位向散焦。图6(b)中径向距离单元熵最大的位置对应的距离单元序号是512,从ISAR图像中可以看出,这个距离单元序号周围并不对应旋转部件,即文献[10]给出的旋转部件距离单元确定规则不够稳健。

(a) 实测数据ISAR图像(a) ISAR image of real data

(b) 径向距离单元熵(b) Range cell entropy图6 某飞机实测数据ISAR图像与径向距离单元熵Fig.6 ISAR image of real data for an airplane and its range cell entropy
按照第2节的方法,进行位置估计,其方位向距离单元熵和局部径向距离单元熵结果如图7所示。从图7(a)中确定目标主体部分所对应的方位向距离单元序号后,对ISAR图像中余下部分进行局部径向距离单元熵的计算,得到图7(b)的结果。由图7(b)可知,旋转部件对应的距离单元序号分别对应490,610,这个结果与ISAR图像中的观测结果一致。在图7(b)中,因为噪声的存在,在进行旋转部件位置检测时,对应的门限是熵均值的5倍,即Λ=5。

(a) 方位向距离单元熵(a) Cross range cell entropy

(b) 局部径向距离单元熵(b) Local range cell entropy图7 位置估计过程中得到的两种熵计算结果Fig.7 Result of two kinds entropy in position estimation
3.3 稳健性分析
通过上述实测数据处理,验证了位置估计方法的有效性,进一步考虑在实测数据中叠加不同幅度的额外噪声,分析该方法的稳健性。
所叠加的噪声模型为:
(6)
式中,randn(1,N)表示长度为N的高斯随机序列,Am为噪声幅度。结合实测数据的情况,N=1024,将Am取两个值1500和2500。
叠加不同幅度的额外噪声之后的ISAR图像与未叠加额外噪声的ISAR图像之间的对比如图8所示。在Am=1500的情况下,目标主体散射结构出现一定模糊,尤其是主体部分,但仍能分辨出成像结果;而在Am=2500的情况下,已经几乎难以分辨目标的散射结构。
按照上述方法对叠加不同额外噪声情况下的ISAR图像进行旋转部件位置估计,所得到的局部径向距离单元熵结果如图9所示。从图中可以看出,在上述两种不同额外噪声幅度下,局部径向距离单元熵的几个极大值对应的位置几乎相同,因此估计出的旋转部件位置是相同的,从而可以认为上述方法对存在噪声的情况具有良好的稳健性,只要ISAR图像中能勉强分辨出目标的散射结构,便可以完成位置估计。

(a) Am=0的ISAR图像(a) ISAR image for Am=0

(b) Am=1500的ISAR图像(b) ISAR image for Am=1500

(c) Am=2500的ISAR图像(c) ISAR image for Am=2500图8 叠加不同幅度额外噪声时的实测ISAR图像Fig.8 ISAR images of real data when additional noise with different amplitude existed

(a) Am=1500局部径向距离单元熵(a) Local range cell entropy when Am=1500

(b) Am=2500局部径向距离单元熵(b) Local range cell entropy when Am=2500图9 叠加不同幅度额外噪声时的局部径向距离单元熵Fig.9 Local range cell entropy result when additional noise with different amplitude was added
4 结论
仿真数据和实测数据结果验证了所提旋转部件位置估计方法的有效性,通过在实测数据中叠加不同幅度的额外噪声,进一步检验了所提出方法对噪声的稳健性。数据处理结果显示,只要能够从数据中获取较为清晰的散射结构,就可以应用本文方法实现ISAR图像中旋转部件位置的自动估计。通过估计旋转部件位置,可以有效支撑HRRP中旋转部件分量分离,进而提升主体部分成像质量。

