基于区间非概率可靠性方法的岩溶区桩基下溶洞顶板稳定性评价

秦 溯，李云安，孙 琳

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

修建于岩溶地区的工程，多采用桩基础来维持上部结构的稳定。实际工程中，许多桩基并未完全穿越下伏溶洞，而是嵌于距溶洞之上一定厚度的基岩中(溶洞顶板)，在保证安全稳定的前提下，可节省一定的工期和成本。因此，对桩基下溶洞顶板稳定性的准确评价显得至关重要。

目前，对于溶洞顶板稳定性的评价方法可大致归结为3类：定性评价法[1-2]、半定量评价法[3-9]和定量评价法[10-15]。其中，定性评价法以综合分析影响溶洞顶板稳定性的因素(顶板岩性、裂隙状况、埋藏条件和地下水等)为基础，结合类似工程经验，对岩溶地基稳定性作出定性的判断。定性评价法可操性强，但评价结果较粗略，主要适用于工程初步勘察阶段或重要程度不高的工程。半定量评价法的一般思路是通过将桩基与溶洞顶板的地质模型进行简化后得到物理模型，然后从力学角度将物理模型转换为数学模型，最后通过将计算结果与实际情况对比来判断桩下溶洞顶板的稳定性。由于半定量评价法可操行强，评价结果可靠，因此在岩溶工程中已得到了广泛的应用。定量评价法一般需先作出适当的假设，然后建立桩基与溶洞相互作用的物理力学模型，并设置适当的边界条件，最后利用计算机强大的计算能力进行分析和计算。虽然定量评价法分析较全面，且所得评价结果直观、可靠，但其实施过程复杂，在实际工程中应用较少。值得注意的是，现有的桩基下溶洞顶板稳定性评价方法多基于确定的参数，即桩参数、溶洞的几何参数、岩土体的物理力学参数等都是确定的值。实际上，由于桩基下溶洞具有隐伏性，加上现有技术条件的限制，很难准确掌握溶洞的真实发育形态和岩土体的物理力学参数值，给溶洞顶板稳定性评价过程带来了较大不确定性。曹文贵等[16]采用三角模糊数表示计算参数取值可能性分布，采用模糊能度可靠性理论，提出了基桩桩端岩溶顶板稳定性模糊能度可靠性分析方法。程晔等[17]将多级模糊评判理论、AHP法和灰色关联分析法相结合，提出了高速公路下伏溶洞顶板稳定性的模糊综合评判法，并结合实际工程进行应用，评判结果能够较准确地反映溶洞顶板的稳定性。赵帅等[18]采用蒙特卡洛抽样法对盐穴储气库顶板安全可靠性进行了分析，通过计算出盐穴储气库顶板的失效概率和可靠性指标来描述其可靠度。可以看出，上述方法的共同点都是以概率(客观概率或主观概率)为基础，需要从一定数量的数据样本中统计出概率特征，而在实际工程中，桩基下溶洞顶板的数据样本数量往往是有限的。

鉴于此，本文引入区间非概率可靠性方法，通过计算出溶洞顶板体系的非概率可靠性指标来判断其稳定性。由工程实例验证了本文方法的合理性与可行性，并对各区间变量的敏感性进行了分析。

1 桩基下溶洞顶板力学简化模型

溶洞顶板在桩基荷载作用下的破坏形式主要有3种，即冲切破坏、剪切破坏和弯拉破坏[19]。根据现有研究成果，假设溶洞顶板岩层产状近乎水平，分别从抗冲切、抗剪切和抗弯角度建立桩基下溶洞顶板力学简化模型，并推导出相应稳定性验算公式。

1.1 抗冲切力学简化模型

溶洞顶板在桩基荷载作用下发生冲切破坏时，冲切体多为圆台状。此时，向上的作用力为作用于冲切体侧面的岩体拉力及作用于冲切体底部的充填物顶托力，具体模型如图1所示。

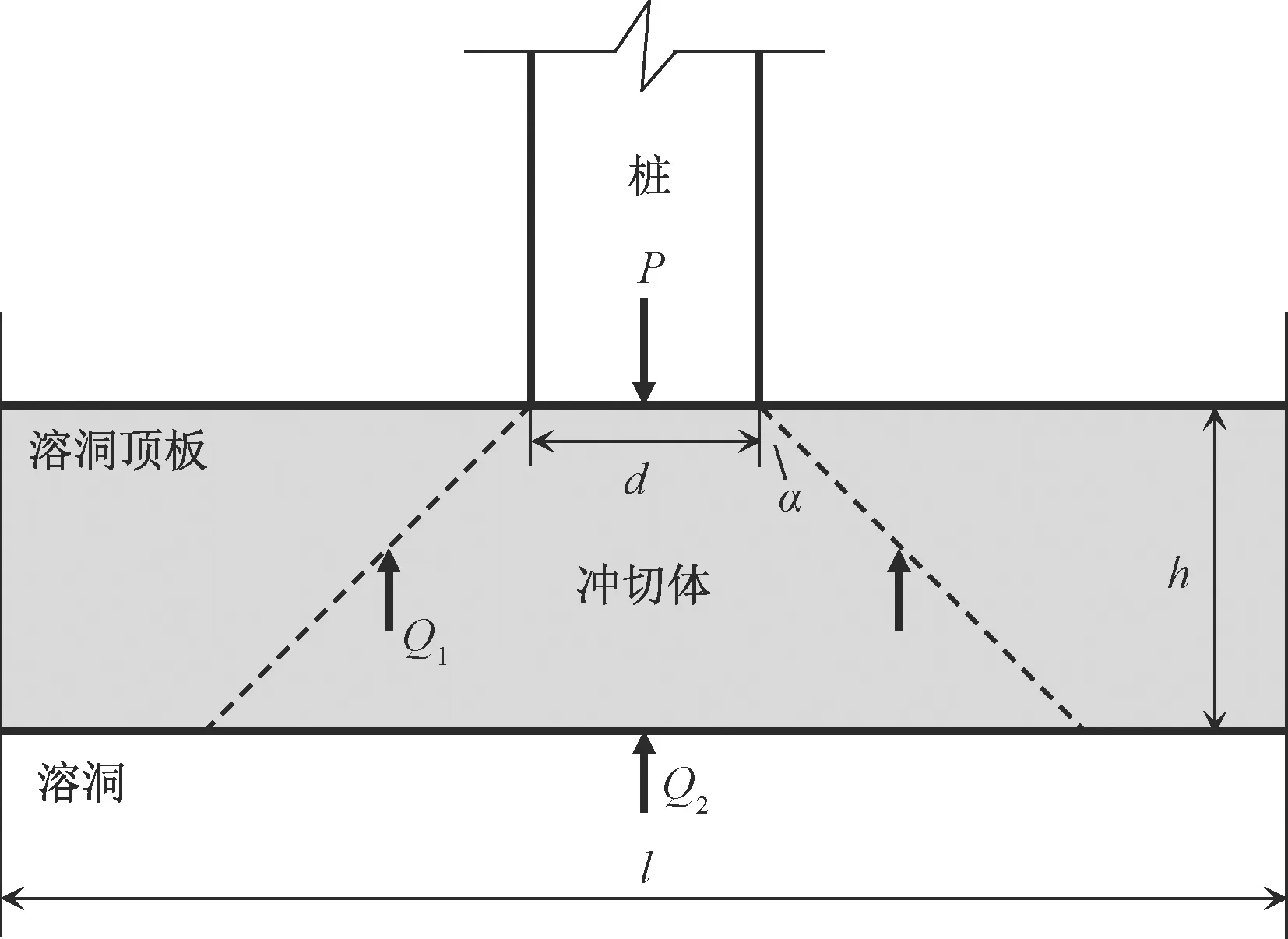
图1 抗冲切力学简化模型Fig.1 Simplified punching mechanical modelP—桩端作用力/kN；Q1—顶板岩体抗拉力/kN；Q2—充填物顶托力/kN；l—溶洞跨度/m；h—顶板厚度/m；d—桩径/m；α—冲切角/(°)

根据力平衡条件可知，维持溶洞顶板稳定而不受冲切破坏，需满足下式：

K1P≤Q1+Q2

(1)

式中，K1为顶板抗冲切安全系数，根据相关规范确定。由于充填物顶托作用微小，基本可以忽略，故视Q2=0。考虑作用于顶板上的桩端作用力P来源于桩顶反力和桩自重，具体计算公式见式(2)。Q1的计算公式见式(3)。

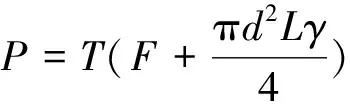
(2)

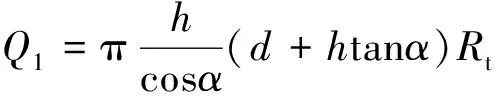
(3)

式中：T——桩端阻力分担比；

F——桩顶反力/kN；

γ——桩体重度/(kN·m-3)；

Rt——顶板岩体抗拉强度/kPa；

L——桩长/m。

其余参数意义同前。

除此之外，当岩体完整性较好，产状近水平时，可取α=45°。为保守起见，将顶板岩体抗拉强度Rt乘以折减系数0.75。联立式(1)、式(2)和式(3)可得：

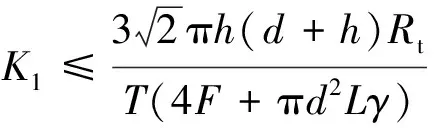
(4)

1.2 抗剪切力学简化模型

溶洞顶板在桩基荷载作用下也可能因为岩体抗剪强度不足而发生剪切破坏，剪切体呈圆柱状，具体模型见图2。图2中，τ为顶板岩体抗剪强度/kPa，其余参数意义同前。

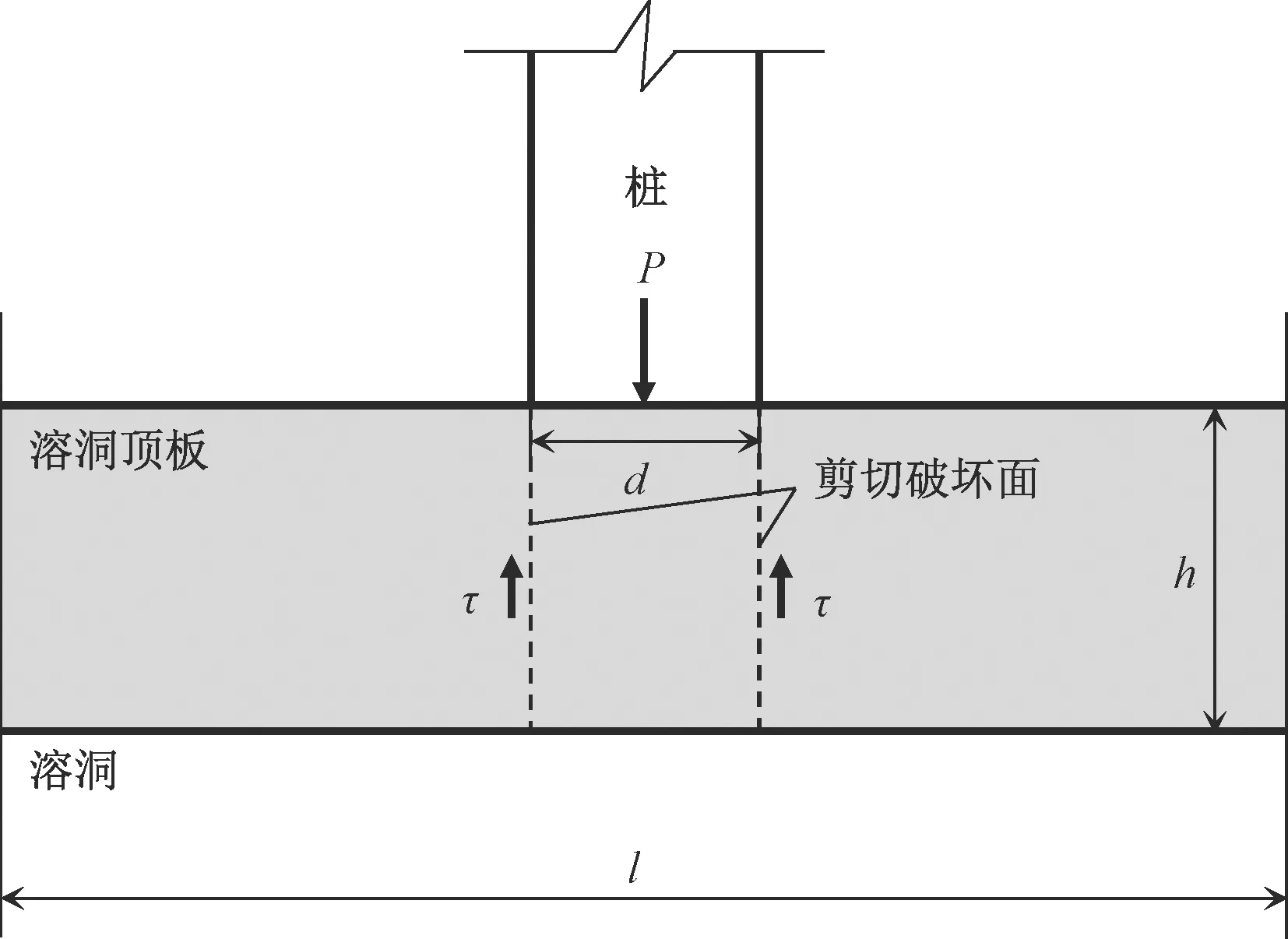
图2 抗剪切力学简化模型Fig.2 Simplified shearing mechanical model

同理，根据力平衡条件可知，维持溶洞顶板稳定而不受剪切破坏，需满足下式：

K2P≤πdhτ

(5)

式中，K2为顶板抗剪切安全系数，根据相关规范确定。将式(2)与式(5)联立可得：

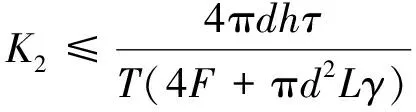
(6)

1.3 抗弯力学简化模型

当溶洞顶板厚跨比较小时，在桩基荷载作用下很可能因为顶板岩体抗弯能力不足而发生弯拉破坏。由结构力学可知，在中部局部荷载的作用下，简支梁的最大弯矩值要大于同几何尺寸下的两端固定梁的最大弯矩值。故出于工程上偏保守的考虑，将溶洞顶板作为简支梁考虑，具体模型见图3。

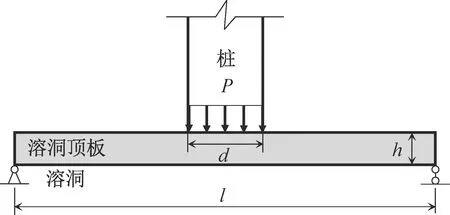
图3 抗弯力学简化模型Fig.3 Simplified bending mechanical model

图3中，通过计算出简支梁中部在局部均布荷载作用下的最大弯矩，进而计算出对应的最大拉应力。当计算出的最大拉应力不大于顶板岩体的抗拉强度时，溶洞顶板稳定而不受弯拉破坏，具体列式如下：

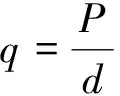
(7)

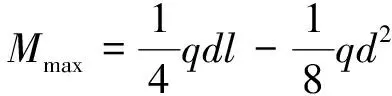
(8)

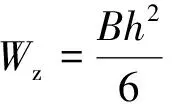
(9)

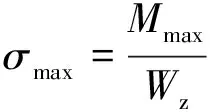
(10)

K3·σmax≤Rt

(11)

式中：K3——顶板抗弯安全系数，据相关规范确定；

B——溶洞宽度/m；

q——考虑桩端作用力下的均布线荷载/(kN·m-1)；

Mmax——考虑桩端作用力下的对应简支梁中部最大弯矩/(kN·m)；

Wz——抗弯截面系数/m3；

其余参数意义同前。

将式(2)与式(7)～(11)联立可得：

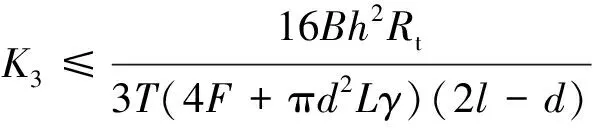
(12)

式(4)、式(6)与式(12)即分别为由对应桩基下溶洞顶板力学简化模型推导出的抗冲切、抗剪切和抗弯稳定性验算公式。

2 桩基下溶洞顶板稳定区间非概率可靠性评价方法

基于前述建立的桩基下溶洞顶板抗冲切、抗剪切和抗弯稳定性验算公式，分别构建出抗冲切、抗剪切和抗弯功能函数g1、g2和g3，并设溶洞顶板体系的功能函数为M，具体列式如下：

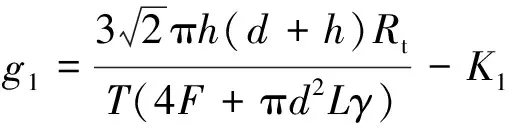
(13)

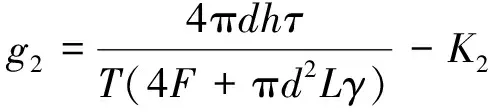
(14)

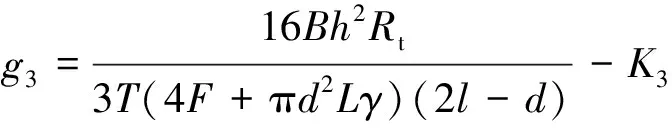
(15)

M=gi(i=1,2,3)

(16)

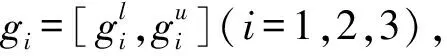
区间运算过程中会产生区间扩展现象，使得响应变量区间变宽而失去真实性。区间截断法是一种能有效解决区间扩展现象的典型方法[20]，其具体实施过程为：设a=[al,au]，b=[bl,bu]为输入区间变量，经区间运算后得到响应区间变量c=[cl,cu]。由输入区间变量a，b对应的中心值a0=(al+au)/2和b0=(bl+bu)/2，求得c的中心值c0=(cl+cu)/2。此时，若c0接近于0，则截断法失效；反之，则用下面的公式分别计算出响应区间变量的上下界限(cu和cl)与其中心值c0的相对偏差Δ1和Δ2。

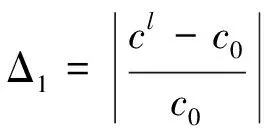
(17)

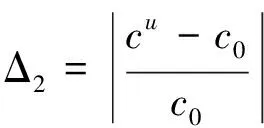
(18)

进一步地，设响应变量的最大相对偏差为2t，t可取所有输入变量相对其中心值偏差最大的值。最后，通过以下条件进行区间截断，并用截断后的区间[dl,du]来代替响应变量c的取值区间。

当Δ1≤t，Δ2≤t时，取

dl=cl

du=cu

当Δ1>t，Δ2>t时，取

dl=c0+t(cl-c0)

du=c0+t(cu-c0)

当Δ1≤t，Δ2>t时，取

dl=cl

du=c0+t(cu-c0)

当Δ1>t，Δ2≤t时，取

dl=c0+t(cl-c0)

du=cu

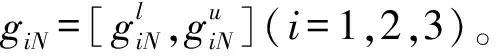
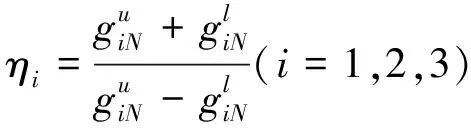
(19)

根据结构可靠性理论可知，当ηi>1(i=1,2,3)时，则相应的功能函数gi>0(i=1,2,3)恒成立，结构稳定可靠；反之，则结构不可靠。桩基下溶洞顶板需同时满足抗冲切、抗剪切和抗弯条件，溶洞顶板体系才算稳定，即溶洞顶板体系的非概率可靠性指标满足η=min{η1,η2,η3}>1时，则溶洞顶板体系安全稳定。

3 工程实例与分析

丹霞高速互通位于中国广东省韶关市境内，包括已建成运营多年的韶赣高速主线(大体呈EW走向)、新建成投入运营的仁新高速(大体呈SN走向)以及8条互通匝道(A～H)。10条线路中，除韶赣高速主线和F匝道全为路基段外，其余线路均含有路基段和桥基段。丹霞高速互通下伏基岩主要为泥盆系锡矿山组砾状灰岩(图4)，为可溶性岩，且地下水运动活跃。经钻探和物探发现该地区岩溶强烈发育(图5)，且存在有桥梁桩基嵌于溶洞顶板之上的情况。为确保线路运营期的安全稳定，需对桩基下伏溶洞顶板进行稳定性评价。以D匝道2#桩下溶洞为例，2#桩桩径d为1.4 m，桩长L为26.0 m。由于勘察技术有限，桩下溶洞的几何参数、物理力学参数等不能准确确定，具有较大的不确定性，故采用区间变量来描述不确定性，具体取值见表1。根据工程要求，为便于计算取顶板抗冲切、抗剪切和抗弯安全系数K1=K2=K3=2。

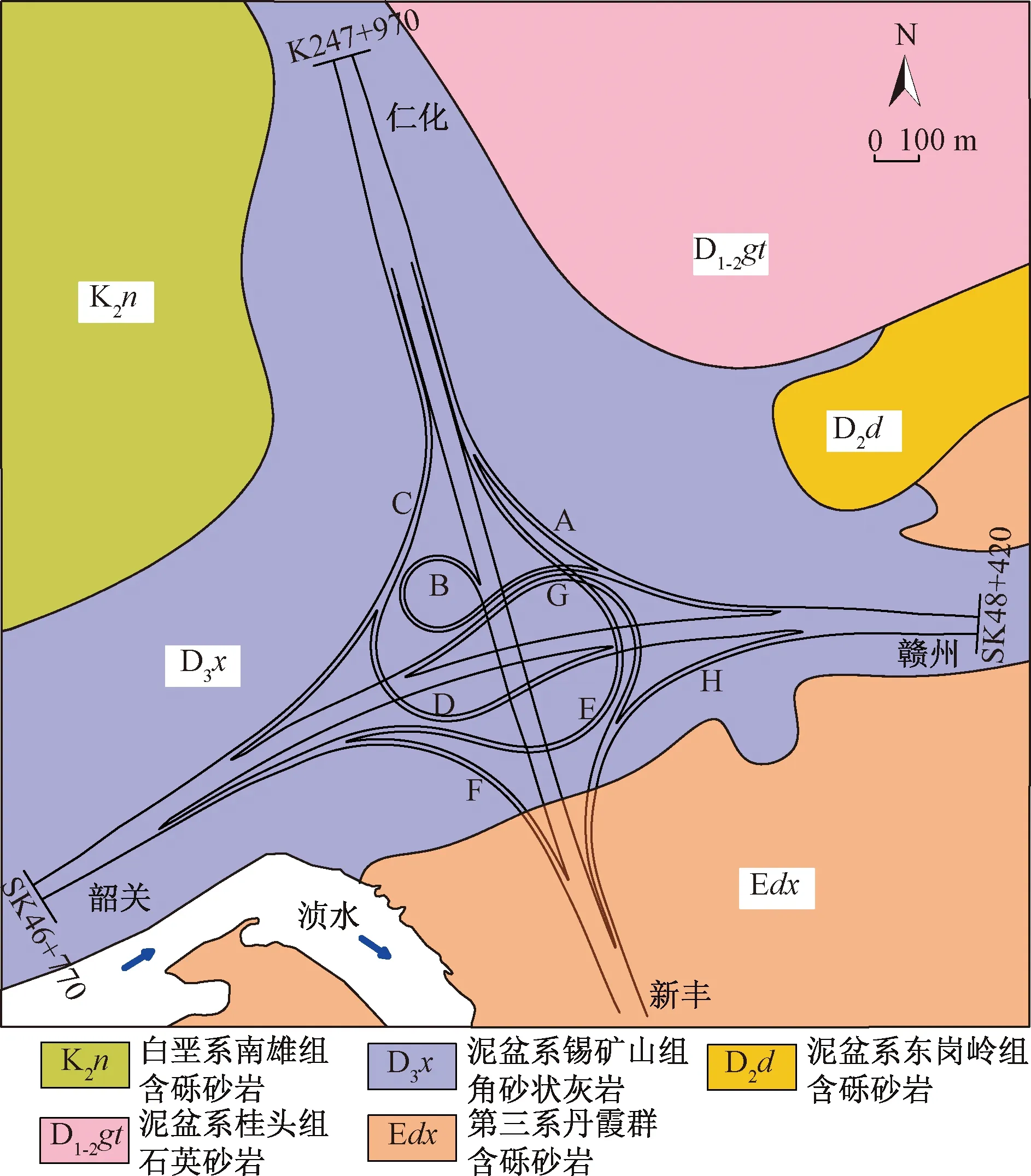
图4 丹霞高速互通工程地质平面图Fig.4 Engineering geological map of the Danxia grade separation area

图5 钻孔揭示溶洞Fig.5 Boreholes revealing the development situation of karst cave

区间变量变量所在区间溶洞顶板厚度h/m[3.4,4.8]溶洞顶板跨度l/m[4.5,5.0]顶板岩体抗拉强度Rt/kPa[4852,5325]顶板岩体抗剪强度τ/kPa[6793,7455]桩顶反力F/kN[4860,5400]桩端阻力分担比T[0.20,0.25]

3.1 区间非概率可靠性方法计算

下面采用前述的区间非概率可靠性方法，分别计算出2#桩下溶洞顶板的抗冲切、抗剪切和抗弯非概率可靠性指标(η1、η2和η3)，进而得到溶洞顶板体系的非概率可靠性指标(η)，通过对比η与1的大小关系来评价桩下溶洞顶板的稳定性。

(1)计算抗冲切非概率可靠性指标η1

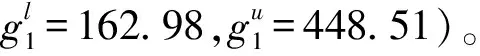
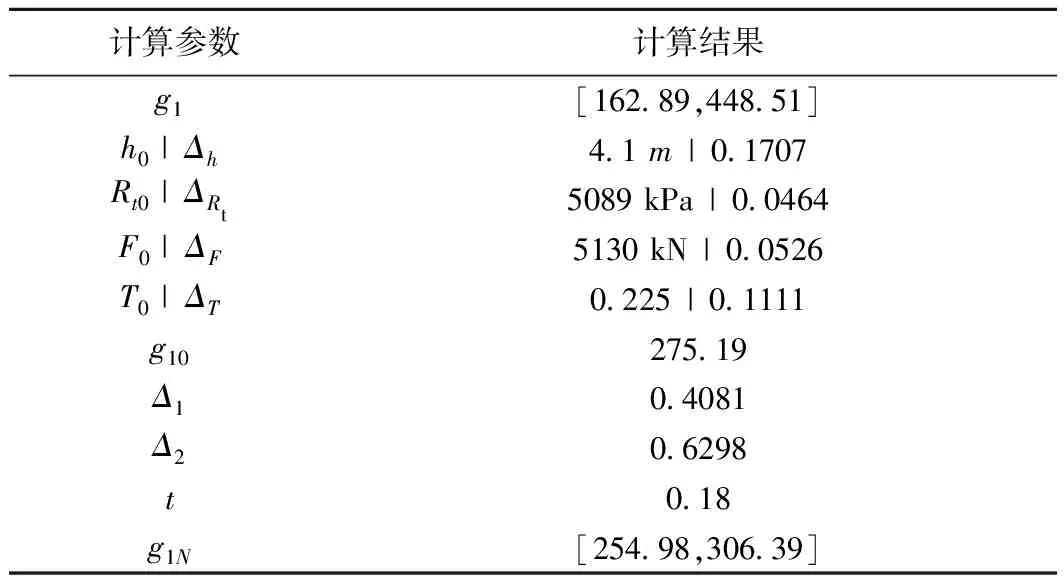
表2 响应区间变量g1区间截断法计算结果

由表2可知，截断后响应区间变量g1N=[254.98,306.39]，根据式(19)可计算出抗冲切非概率可靠性指标η1=10.92。

(2)计算抗剪切非概率可靠性指标η2

同理，将参数代入式(14)，利用INTLAB区间运算工具箱得到响应区间变量g2=[61.48,132.28]，采用区间截断法缩小区间扩展，计算结果见表3。

由表3可知，截断后响应区间变量g2N=[85.79,98.54]，根据式(19)可计算出抗剪切非概率可靠性指标η2=14.46。

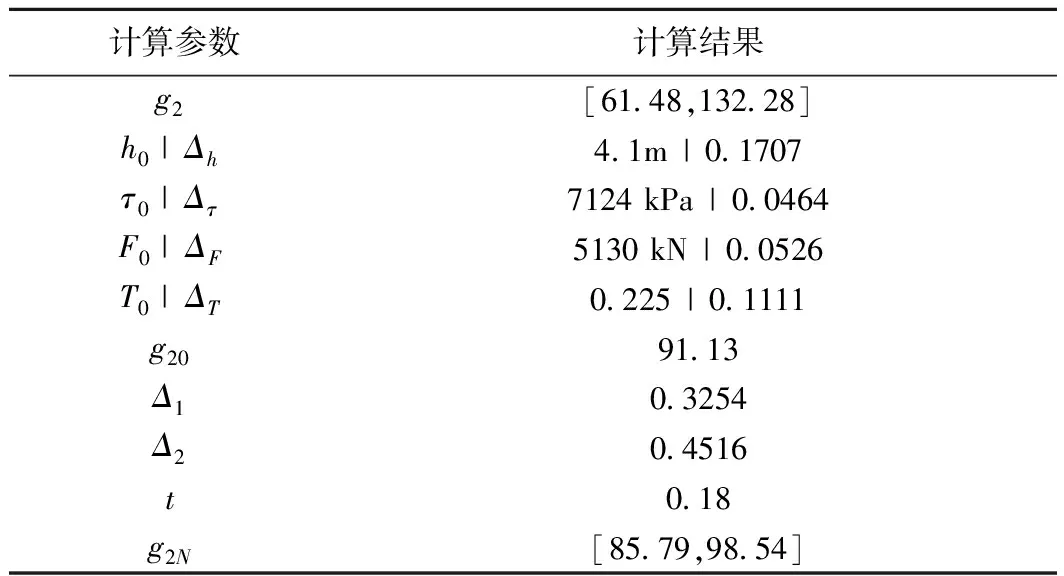
表3 响应区间变量g2区间截断法计算结果

(3)计算抗弯非概率可靠性指标η3

将参数代入式(15)，经区间运算得到响应区间变g3=[22.46,89.82]，其截断后的结果见表4。

表4 响应区间变量g3区间截断法计算结果

由表4可知，截断后响应区间变量g3N=[42.16,54.29]，根据式(19)可计算出抗弯非概率可靠性指标η3=7.95。

通过上述计算可知，2#桩下溶洞顶板体系的非概率可靠性指标η=min{10.92,14.46,7.95}=7.95，大于1，进而可判断出2#桩下溶洞顶板是稳定的。事实上，丹霞高速互通中D匝道自建成通车至今，运营状态良好，未出现桩基失稳问题，说明了本方法具有较好的工程实用性。

3.2 区间变量敏感性分析

为进一步研究区间变量的变异性对桩下溶洞顶板非概率可靠性指标的影响规律，引入变异系数C。以建立的抗冲切、抗剪切和抗弯功能函数为单位，研究当各功能函数中区间变量的变异系数C不同时(C从0.01递增至0.1)，对应的非概率可靠性指标ηi(i=1,2,3)的变化规律。在区间变量敏感性分析过程中，每次只改变一个区间变量。最后得到各非概率可靠性指标与各区间变量变异系数的变化曲线，见图6～8。

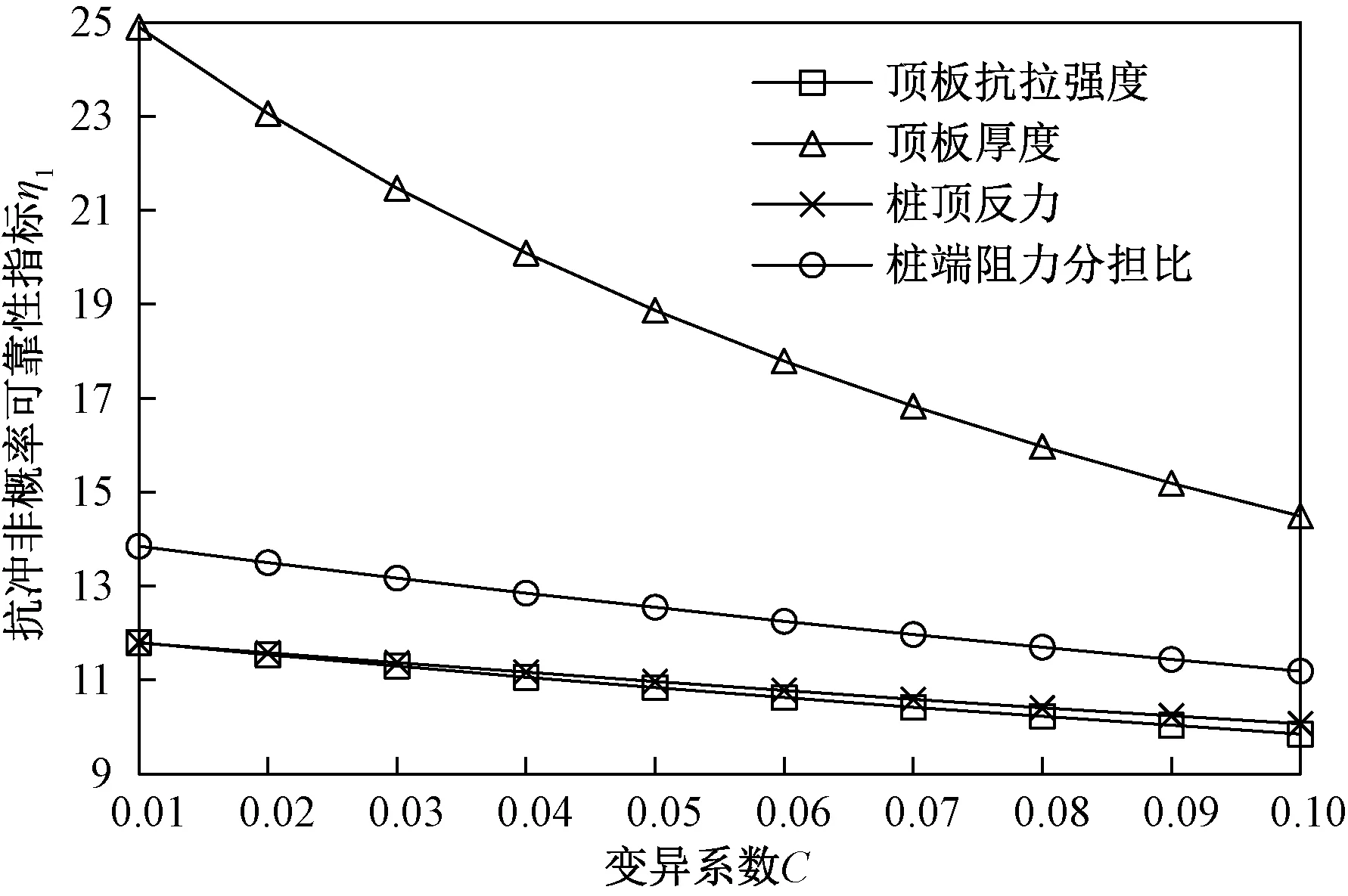
图6 抗冲切非概率可靠性指标与各区间参数变异系数曲线Fig.6 Curve of the punching non-probabilistic reliability index and the coefficient of variation of each interval parameter

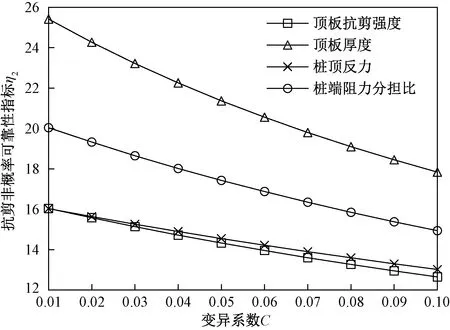
图7 抗剪切非概率可靠性指标与各区间参数变异系数曲线Fig.7 Curve of the shearing non-probabilistic reliability index and the coefficient of variation of each interval parameter

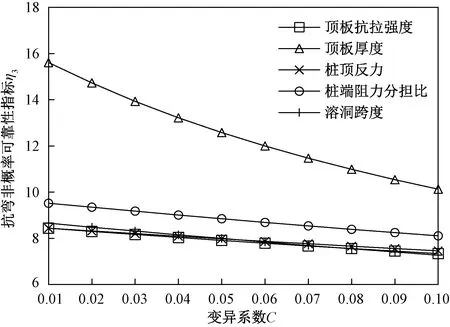
图8 抗弯非概率可靠性指标与各区间参数变异系数的曲线Fig.8 Curve of the bending non-probabilistic reliability index and the coefficient of variation of each interval parameter

从图6～8可以看出，总体上来说，3种非概率可靠性指标(η1、η2和η3)随各区间变量变异系数的增大而降低，但降低程度不同。笔者通过计算出各曲线的割线斜率绝对值K来描述敏感性的大小，曲线对应的割线斜率绝对值越大，相应的非概率可靠性指标随区间变量变异系数增大而降低的程度就越大，敏感性也就越高。图6中，各曲线的割线斜率绝对值计算结果及排序为：K1-h(115.67)>K1-T(29.56)>K1-Rt(21.67)>K1-F(19.11)；图7中，各曲线的割线斜率绝对值计算结果及排序为：K2-h(84.33)>K2-T(56.57)>K2-τ(37.67)>K2-F(33.44)；图8中，各曲线的割线斜率绝对值计算结果及排序为：K3-h(60.89)>K3-T(15.67)>K3-l(15.44)>K3-Rt(12.22)>K3-F(10.89)。通过上述计算结果可明显看出，溶洞顶板厚度h的变异性对3种非概率可靠性指标影响最大，其次为桩端阻力分担比T，桩顶反力F的影响相对最小。由此可见，在进行桩基下溶洞顶板区间非概率可靠性分析时要特别注意区间变量的变异系数，只有将区间变量的变异系数控制在一定范围内，才能得到更准确的溶洞顶板稳定性评价结果。

4 结论

(1)桩基下溶洞顶板稳定区间非概率可靠性评价方法以抗冲切、抗剪切和抗弯稳定性验算公式为基础建立功能函数，借助MATLAB中的INTLAB区间运算工具箱进行区间运算，并采用区间截断法消除运算过程中的区间扩展现象，最后通过比较溶洞顶板体系的非概率可靠性指标η与1的大小来判断桩基下溶洞顶板的稳定性。

(2)以丹霞高速互通中D匝道2#桩基下溶洞为例，计算出该桩基下溶洞顶板体系的非概率可靠性指标η=7.95>1，溶洞顶板处于稳定状态。该评价结果与工程实际相符，表明了本方法的合理性与可行性。

(3)随各区间变量变异系数的增大，相应非概率可靠性指标呈不同程度的降低，其中溶洞顶板厚度h的变异性对评价结果影响最大，其次为桩端阻力分担比T，桩顶反力F的影响相对最小。因此，得到准确评价结果的前提是将各区间变量的变异系数控制在合理范围以内。