钢管混凝土拱桥在桥面激振频率下的动力特性

周 潮 泳

(浙江工业大学建筑工程学院，浙江 杭州 310014)

1 概述

钢管混凝土系杆拱桥因其跨越能力强、外观优美等优点，在我国得到了广泛的应用[1]。钢管混凝土作为一种由钢管与混凝土组成的组合结构，将两种材料各自的优势最大程度地发挥，并将两种材料的劣势相互弥补，使得拱桥发展的各类难题得以解决，拱桥的发展翻开崭新的篇章。

桥梁在服役过程中长期受到车辆动力荷载的作用，而随着车辆轴重、速度的不断增大，桥梁结构的安全与稳定性受到极大考验[2]，因此桥梁动力响应方面的研究也受到越来越多学者的关注。李小珍[3]采用分离迭代法，分别建立了车辆和桥梁的动力学运动方程，对车桥耦合振动的数值计算方法进行了完整的阐述。程保荣和周玉勋[4]采用模态综合分析法对少自由度的车桥耦合系统进行动力特性分析。张军[5]对在此少自由度的车桥耦合系统上进一步简化，仅考虑自由度较多的桥梁子系统，而忽略车辆子系统进行车桥系统耦合振动方程的推导求解。施颖[6]、安里鹏[7]、沈阳超[8]、罗浩[9]等人对连续梁桥进行车桥耦合分析，柳鑫[10]、杨磊[11]、王晓春[12]、朱劲松[13]等人针对悬索桥进行动力响应研究。我国目前对连续梁桥及悬索桥动力响应的研究已经趋于成熟，相对而言，钢管混凝土系杆拱桥动力响应的研究相对滞后。张强[14]在ANSYS中建立空间有限元模型，对某钢管混凝土拱桥进行了车桥耦合振动动力特性分析，结果表明冲击系数与车速并非是正相关关系。赵露薇[15]针对桥梁阻尼对桥梁冲击系数的影响，对某钢管混凝土拱桥进行了研究。肖静霆[16]利用ANSYS中对某系杆拱桥进行了三维全桥模型建立，分析了车辆轴重对桥梁动力特性的影响。

目前钢管混凝土系杆拱桥动力特性的研究多采用有限元软件

模拟分析法，且考虑因素多为车辆轴重、车辆速度、车辆行进路线、路面随机不平顺等，较少考虑桥面激振频率下的不平顺因素对系杆拱桥动力响应的影响。因此，本文以淮安市某钢管混凝土系杆拱桥为工程背景，开展行车荷载下桥梁振动特性研究，利用有限元软件ABAQUS建立系杆拱桥车桥有限元模型，通过现场实测结合有限元数值模拟就桥面激振频率下的不平顺对系杆拱桥动挠度的影响展开研究。

2 现场试验实测

某钢管混凝土系杆拱桥位于淮安市，桥梁结构主要由系梁(2根)、横梁(17根)、拱肋、桥面板、吊杆以及风撑组成。桥梁拱肋为下承式钢管混凝土系杆拱，计算跨径L=85 m，计算宽度为B=12.8 m，矢跨比f/L=1/5，最大桥梁矢高为f=17 m，拱轴线采用二次抛物线。拱肋采用哑铃型钢管混凝土，截面高度为1.9 m，上下钢管直径为0.8 m，壁厚1.4 cm，钢管内填充C40微膨胀混凝土；每片拱设间距为5.3 m的吊杆15根，采用PESFD7—55低应力防腐拉索；系梁采用箱型截面，梁高1.8 m，宽1.4 m。桥梁立面及挠度测点示意图见图1。

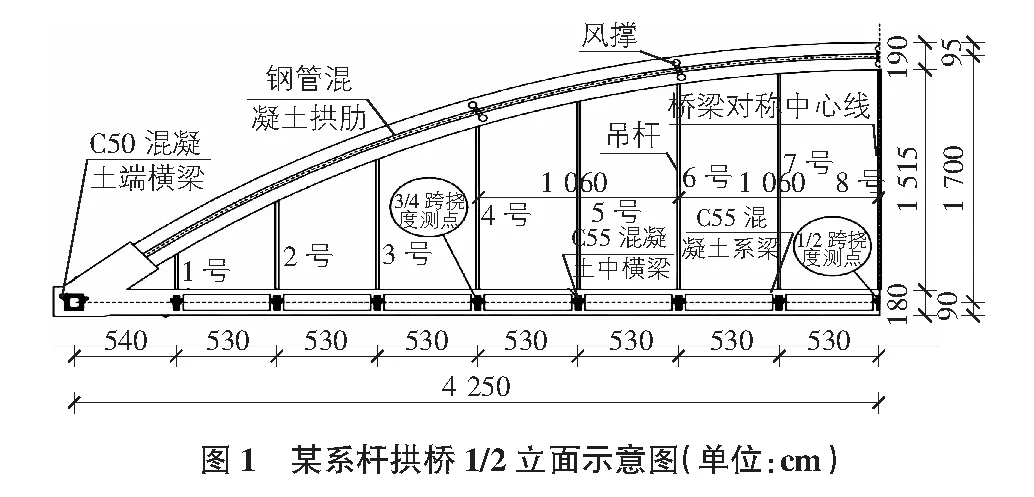
现场试验选用轴重10 t(车辆总重25 t)的三轴装载车以30 km/h的速度沿桥梁中线匀速行驶。为模拟桥面不平顺工况，现场桥面从桥梁跨中往桥梁两端布置11道等间距的凸起减速条带，如图2所示，其中每根减速条带尺寸为：长度1 m、宽度0.15 m、高度0.03 m，减速条带具体摆放数量与间距如表1所示。在恒定车速30 km/h情况下，凸起减速条带的间距变化将引起不同大小的桥面激振频率，实测不同大小桥面激振频率下的桥梁1/2跨与3/4跨处的动挠度。

表1 桥面激振频率工况

车速km/h激振频率/Hz路面突起物间隔/m轴重/t车辆行进位置道路凸起带道数3024.1710桥梁中线113051.6710桥梁中线11

由表2可知：2 Hz和5 Hz激振频率下的1/2跨和3/4跨处最大挠度值均呈现随着激振频率的增加而减小的趋势，同时1/2跨动挠度最值均小于3/4桥跨动挠度。

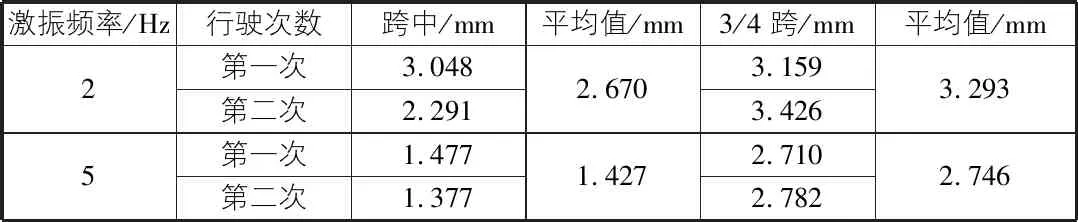
表2 不同激振频率下桥梁动挠度最大值

3 有限元数值分析

3.1 有限元模型建立

在ABAQUS中的全桥模型示意图如图3所示，其中拱肋、吊杆、风撑、系梁以及横梁采用梁单元分析计算，桥面板采用板单元分析计算并设置与现场尺寸一致的减速凸起条带，同时将桥面板与其下各横梁绑定，驱使横梁随桥面板共同上下移动。边界条件设置为桥梁四角点全局指定位移转角固定以还原现场固定盆式橡胶支座连接。桥梁各构件截面尺寸以及材料参数与实际桥梁相同，见表3。

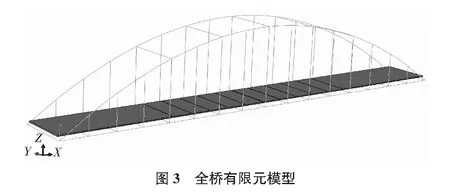
表3 桥梁构件截面尺寸及材料参数

构件单元类型截面形式截面尺寸/m材料弹性模量/Pa密度kg/m3泊松比拱肋梁单元广义—C403.25×10102 5000.2风撑梁单元圆形0.35Q345C2.06×10117 8500.3吊杆梁单元圆形0.13Q345C2.06×10117 8500.3系梁梁单元箱型1.4×1.8C553.55×10102 5000.2端横梁梁单元箱型1.5×1.6C503.45×10102 5000.2中横梁梁单元矩形0.6×1.3C553.55×10102 5000.2桥面板板单元矩形10×0.25C503.45×10102 5000.2

建立与实际三轴装载车尺寸一致的车辆模型，考虑车辆自由度为车体浮沉位移、摇头角位移、点头角位移以及三对车轮的浮沉位移，总计9个自由度，通过相互作用设置自由度并模拟车辆悬挂系统，如图4，图5所示。车辆尺寸、质量、刚度、阻尼等参数见表4。

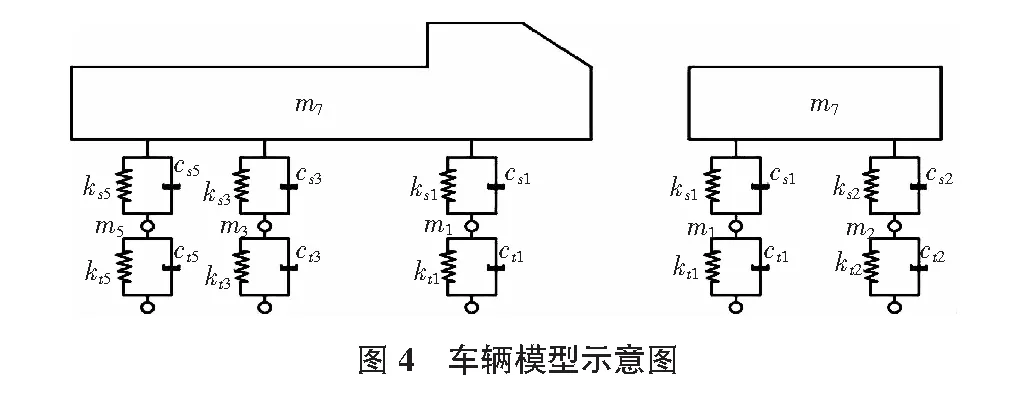
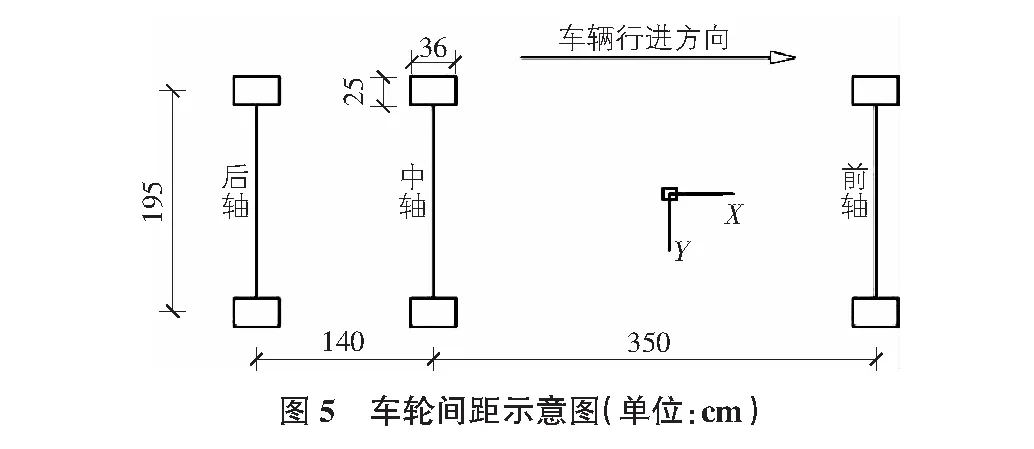
表4 车辆模型参数

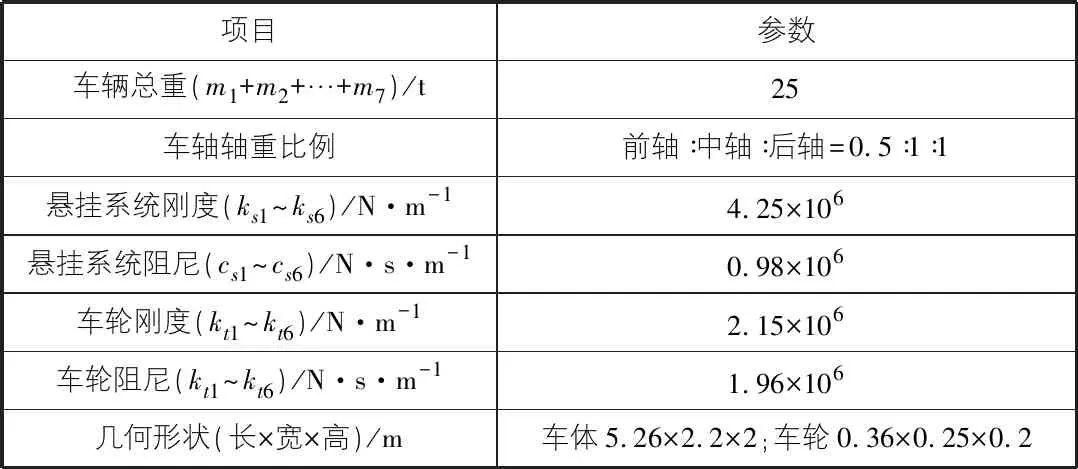
项目参数车辆总重(m1+m2+…+m7)/t25车轴轴重比例前轴∶中轴∶后轴=0.5∶1∶1悬挂系统刚度(ks1～ks6)/N·m-14.25×106悬挂系统阻尼(cs1～cs6)/N·s·m-10.98×106车轮刚度(kt1～kt6)/N·m-12.15×106车轮阻尼(kt1～kt6)/N·s·m-11.96×106几何形状(长×宽×高)/m车体5.26×2.2×2;车轮0.36×0.25×0.2

3.2 实测结果及有限元模型验证

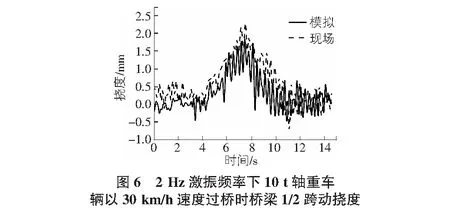
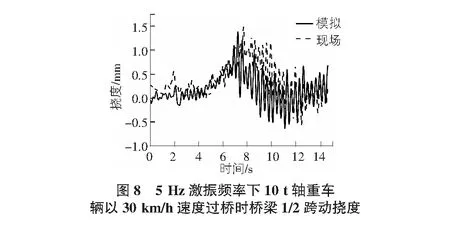
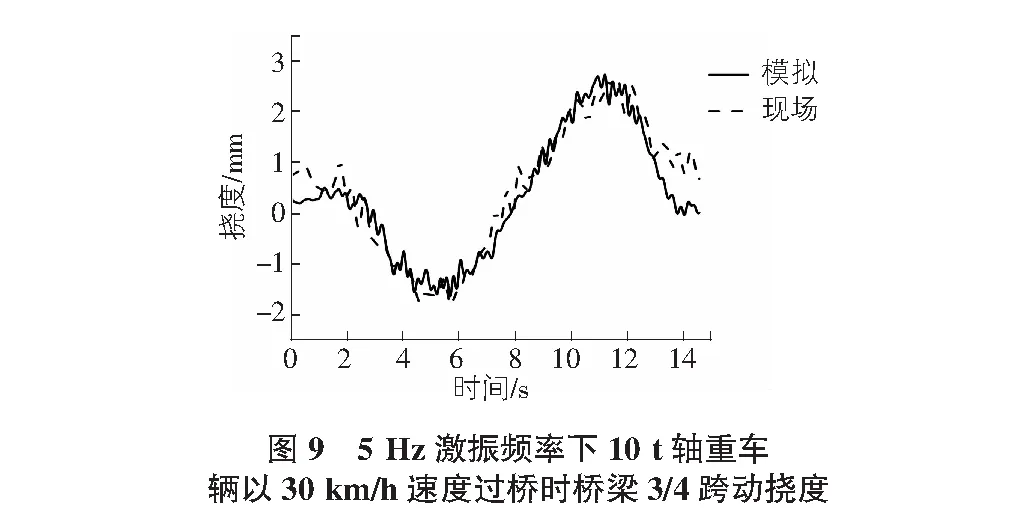
选择轴重10 t车辆以30 km/h的速度沿桥梁中线，通过凸起带设置间距模拟桥面激振频率使其与现场频率相同，为2 Hz及5 Hz。对现场实测结果与有限元数值模拟结果的动挠度时程曲线进行对比，结果如图6～图9所示，由图可知：2 Hz及5 Hz工况下，现场实测与有限元数值模拟动挠度时程曲线的趋势与最值基本吻合，说明有限元模型的正确性。

3.3 有限元模型分析

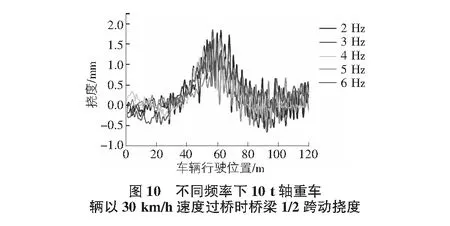
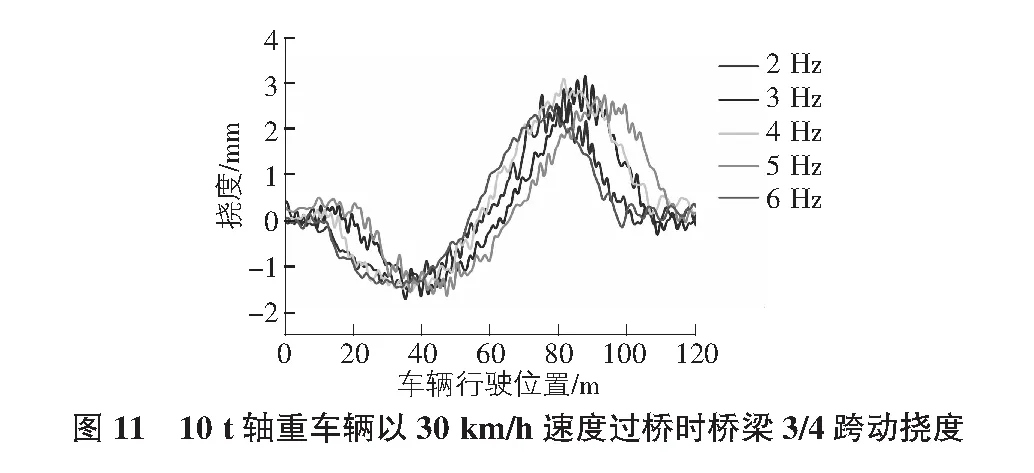
通过现场实测结果与有限元数值模拟结果的动挠度时程曲线对比验证有限元模型的正确性后，在此模型上添加更多工况对不同桥面激振频率影响下桥跨的动力响应进行分析。选择轴重为10 t的车辆，控制车辆速度为30 km/h沿桥梁中线行驶，桥梁1/2跨、3/4跨处的动挠度变化曲线见图10，图11。由图可知，3 Hz激振频率下的最大动挠度值大于其他激振频率下的最大动挠度值，5 Hz与6 Hz激振频率下的最大动挠度值小于其他激振频率下的最大动挠度值，桥跨最大动挠度值随着激振频率的增大而减小。根据现场桥梁基频测试资料可得该系杆拱桥一阶竖向自振频率为2.934 Hz，与3 Hz最为接近，因此3 Hz激振频率下的最大动挠度值最大。同时，通过对比桥梁1/2跨与3/4跨动挠度变化曲线可知，10 t轴重车辆以30 km/h沿桥梁中线行驶时，桥梁3/4跨动挠度比1/2跨动挠度大。

4 结语

本文对淮安市某钢管混凝土系杆拱桥进行了现场行车试验，同时在ABAQUS中建立了空间车桥耦合振动数值模型，将现场实测结果与数值模拟结果进行对比验证了数值模型的正确性。在此基础上，分析了桥面激振频率下的不平顺工况的该系杆拱桥的动挠度值，有以下结论：

1)系杆拱桥最大动挠度值与桥面激振频率并无正负相关关系。

2)桥面激振频率与桥梁基频越接近，系杆拱桥的最大动挠度值越大。

3)不同桥面激振频率下，系杆拱桥3/4跨处的最大动挠度值较1/2跨处大。