基于阻尼层多目标动力学拓扑优化的车内噪声控制

张 宇 ，曹友强

(1. 重庆电子工程职业学院 汽车工程学院，重庆401331； 2. 吉利汽车研究总院，浙江 宁波315336)

0 引 言

车辆行驶状态下车内噪声水平是衡量NVH性能的重要指标，亦是影响消费者购车行为的主要因素之一。合理使用阻尼材料可提高车身壁板的吸隔声性能，从而降低车内低频结构噪声[1]。因此，如何在车身壁板上设计合理的阻尼材料便成为当前NVH技术研究的焦点之一。

传统的方法是基于车身结构模态应变能和板件贡献量来确定阻尼敷设位置[2-4]。模态应变能云图取值范围不同会导致设计的阻尼材料布局各异。这往往给工程化实施带来困扰。但是近年来随着动力学拓扑优化技术的发展，为车身阻尼材料布局优化提供了新的方法[5-6]。

不少文献对车身局部阻尼材料的减振降噪性能进行了研究。例如，文献[7]研究了地板阻尼涂层对车内噪声的影响，并使车内加速噪声峰值下降了2～4 dB(A)；文献[8]研究了顶盖自黏型约束阻尼材料布置优化形式，使车内噪声下降了1.0～2.2 dB(A)；文献[9]采用拓扑优化方法对地板热熔型自由阻尼材料布置进行优化，使车内噪声下降了2.3 dB(A)。但是鲜有关于车身阻尼材料总体布局研究的文献。

针对某车型车内噪声问题，以壁板贡献度和模态贡献度为参考指标，采用多目标动力学拓扑优化方法对整车阻尼材料布局进行综合设计，以期达到改善车内噪声性能的目的，并为整车阻尼材料总体布置提供一种有效的设计方法。

1 复合阻尼结构基本理论

通常为达到减振降噪的目的，以车身不同区域壁板作为基板，敷设面积不等、种类各异的阻尼材料，从而构成复合阻尼结构，并采用复常数模量描述其黏弹性材料的本构关系，复合阻尼结构系统自由振动方程为

[M]{ü}+[K′+iK″]{u}=0

(1)

式中：[M]为质量矩阵；[K′+iK″]为复刚度矩阵。

设式(1)的特解为

{u}={Ψ}eλt

(2)

则将式(2)代入式(1)得：

(λ2[M]+[K′+iK″]){Ψ}=0

(3)

求特征值方程：

|λ2[M]+[K′+iK″]|=0

(4)

可得复特征值：

λi=α+iβ

(5)

式中：α为解的实部；β为解的虚部。

进而可以得到复合阻尼结构第i阶模态的固有频率fi和模态阻尼损耗因子ηi：

(6)

(7)

模态阻尼损耗因子ηi一般为阻尼比的2倍。模态损耗因子描述的是系统能量的衰减，阻尼比描述的是振动幅值的衰减[10]。

因此，为使复合阻尼结构具有最佳的阻尼比和模态损耗因子，可选取降低基板振动幅值为优化目标，借助拓扑优化技术获得阻尼材料最佳布局。

2 车内噪声仿真分析

车辆行驶过程中，路面、动力总成系统、进排气系统、传动系统等外部激励源将振动传递至车身结构，导致车身壁板振动从而产生辐射噪声。基于上述机理，声固耦合仿真分析技术可作为模拟车内噪声性能的一种有效手段。

2.1 车内噪声仿真计算

以某车型为研究对象，运用HyperWorks有限元仿真软件，建立由白车身、开闭件、玻璃和声腔构成的声固耦合仿真分析模型。其中，车身焊点结构采用ACM单元模拟；车身钣金结构采用单元尺寸为10 mm的板壳单元离散；车内声腔结构采用单元尺寸为60 mm的流体单元离散。最终构成的声固耦合仿真分析模型包含55.2万个固体单元，18.7万个流体单元。为模拟车辆匀速行驶状态，在前、后悬架安装点施加20～200 Hz的单位激振力(见图1)。

图1 某车型声固耦合仿真分析模型Fig. 1 Acoustic-structure coupling simulation analysis model for acertain vehicle

选择驾驶员右耳位置(DR测点)和后排座椅中间位置(RM测点)作为车内噪声响应点。计算获得DR测点和RM测点噪声响应见图2。可见该车型DR测点和RM测点在118 Hz均存在明显异常噪声峰值。这类低频噪声极易导致驾乘人员乘坐舒适性恶化，必须采取措施加以改善。

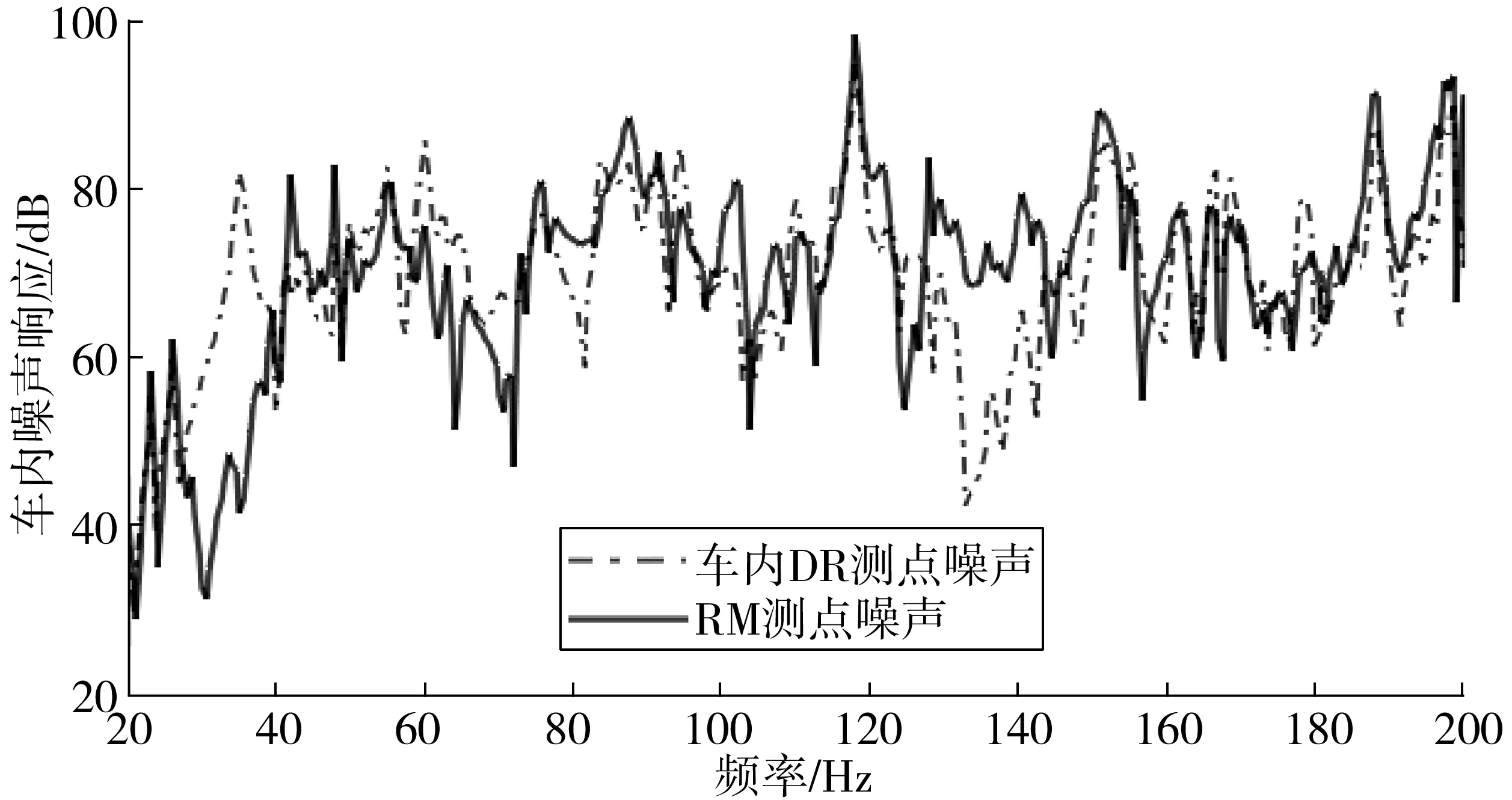
图2 车内噪声仿真计算结果Fig. 2 In-car noise simulation calculation results

2.2 壁板贡献度分析

20～200 Hz频段的车内低频噪声主要是由车身壁板振动所产生的结构噪声，车内噪声测点处的声压可以认为是各板件振动引起的声压叠加。对构成车室声腔的壁板进行贡献度分析，可以获取各壁板对关注噪声频率的影响程度，从而便于确定振动噪声源位置。

为找出导致车内噪声异常峰值的壁板，先分别以DR测点和RM测点118 Hz噪声峰值为对象，计算构成车室声腔主要大面积壁板的噪声贡献度，再将两测点的壁板噪声贡献。

贡献度进行加权求和，得到计算结果见表1。可见，前围板、前车门内板和后地板对车内噪声的贡献度远大于其他壁板。同时，前门内板对DR测点异常噪声峰值贡献量最大，后地板和前围板对RM测点异常噪声峰值贡献量最大。因此，为有效、精准地改善车内噪声性能，应在上述车身壁板合理的敷设阻尼材料。

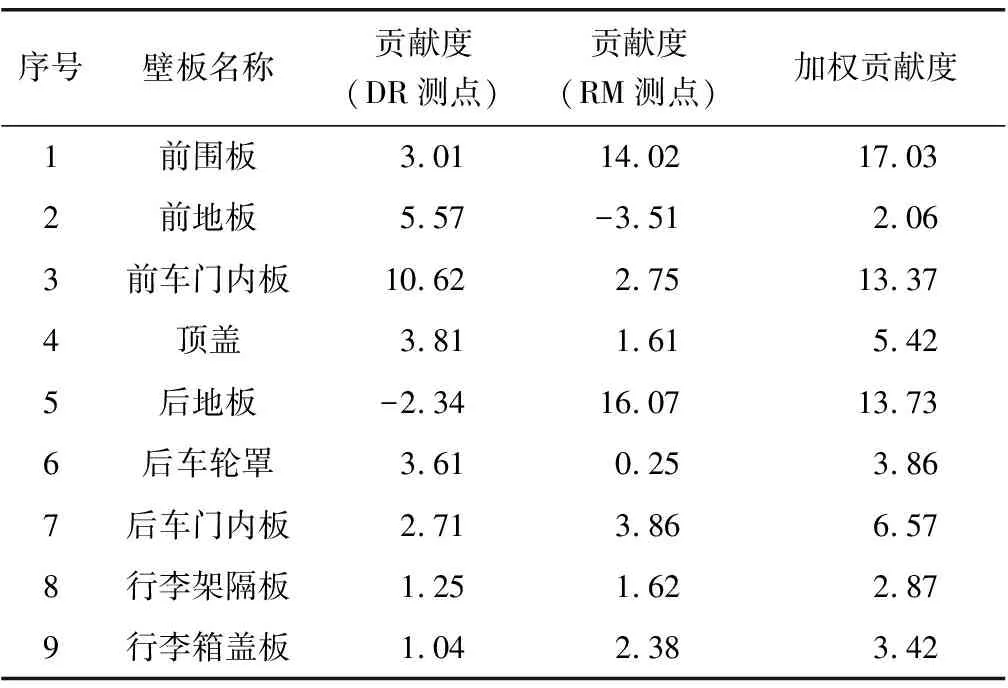
表1 车身壁板贡献度Table 1 Contribution of body panels %

2.3 模态贡献度分析

模态贡献度能反映系统每阶结构模态对车内声学响应的参与量。为了识别对车内异常噪声峰值贡献度最大的结构模态阶次，分别针对DR测点和RM测点在118 Hz处的噪声峰值进行结构模态贡献度分析(见图3)。

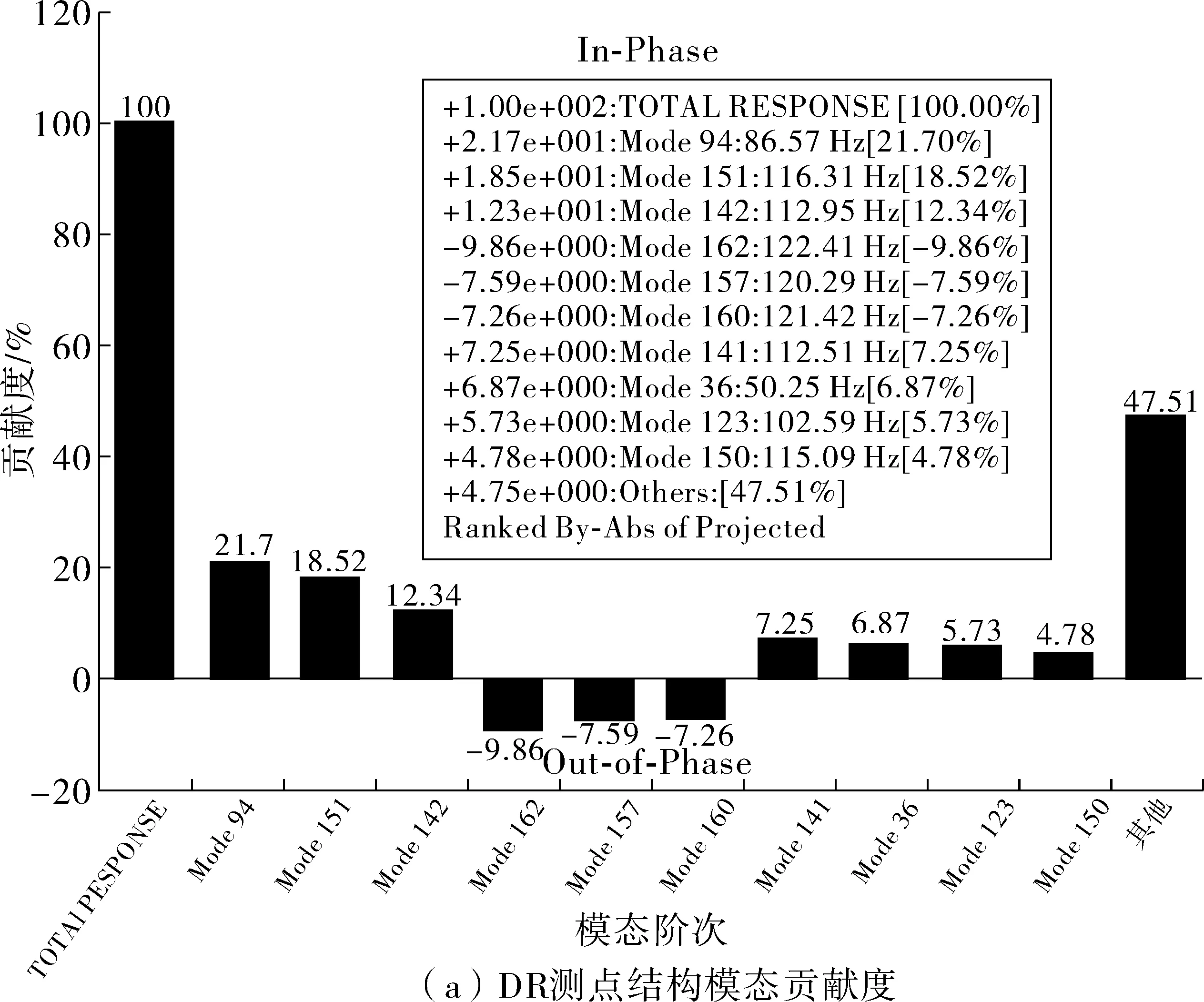
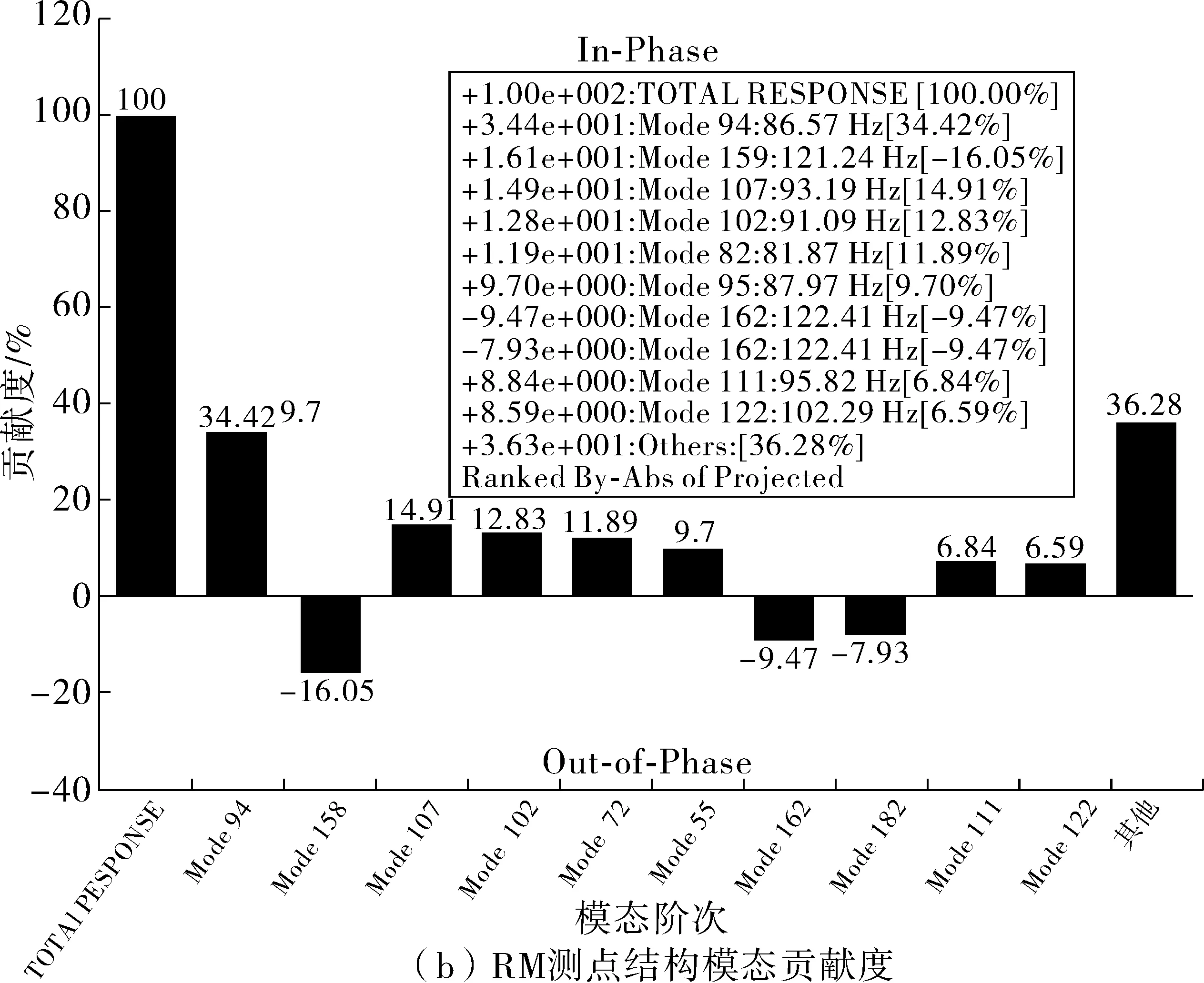
图3 车内噪声测点结构模态贡献度Fig. 3 Mode contribution of noise measurement points in car

由图3可知，对DR测点118 Hz噪声峰值模态贡献度较大的模态阶次为94阶、151阶和142阶，对RM测点118 Hz噪声峰值模态贡献度较大的模态阶次为94阶、107阶、102阶和82阶。

3 车身阻尼材料优化设计

为充分利用阻尼材料的减振降噪性能来改善车内噪声水平，需要对车身阻尼材料布局进行优化设计。而拓扑优化技术通过在给定设计空间内寻求最佳的结构分布形式，来达到优化结构的目的。这为寻求车身阻尼材料的最佳布局提供了一种便捷的手段。

3.1 阻尼材料拓扑优化模型

利用多目标动力学拓扑优化技术，对车身阻尼材料总体布局进行设计，实现尽量少用材料且达到改善车内噪声的目的。为此，建立的多目标动力学拓扑优化数学模型如下：

(6)

3.2 阻尼材料设计

根据上述数学模型，通过壁板贡献度分析和模态贡献度分析结果，计算得到敏感车身壁板在主要贡献模态阶次的综合模态振型应变能见图4，综合模态应变能突出区域见图4中的A～F点。

图4 车身敏感壁板综合模态应变能Fig. 4 Comprehensive modal strain energy of car sensitive panel

为建立合理的拓扑优化模型，结合车身壁板几何结构和阻尼材料敷设工艺要求，首先在前门内板、前围板和后地板敷设阻尼材料初始布局(见图5中白色线框区域)，并分别选取自黏型约束阻尼材料、自黏型自由阻尼材料和热熔型自由阻尼材料。各类型阻尼材料性能参数见表2。

根据式(6)提出的拓扑优化方法，拾取图4中综合模态应变能突出的A-F点为关键点，分别计算求得各关键点的法向频响位移最大幅值以及加权系数αi，从而构建多目标动力学拓扑优化目标函数。随后，运用HyperWorks软件平台中的Optistruct软件，计算获取车身阻尼材料单元密度云图，见图5。

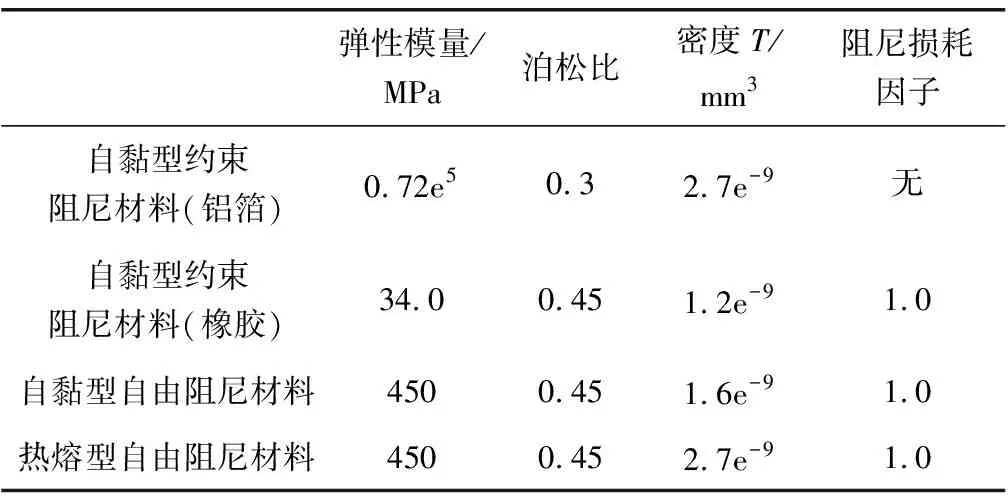
表2 阻尼材料性能参数Table 2 Performance parameters of damping material

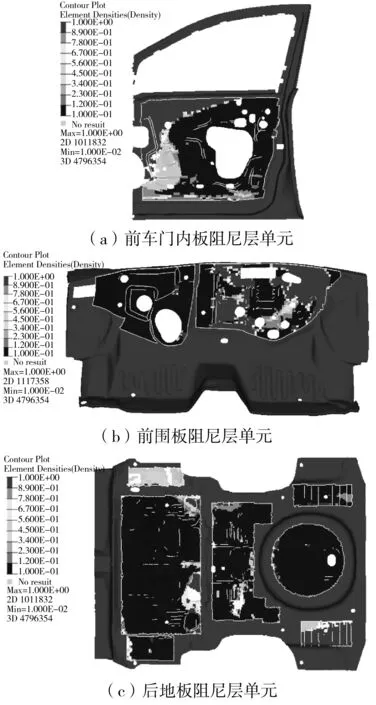
图5 车身敏感壁板阻尼层单元密度云图Fig. 5 Cell density nephogram of damping layer of carsensitive panel

由图4、图5车身敏感壁板的综合模态应变能云图和阻尼层单元密度云图，分别采用在车身壁板模态应变明显区域敷设阻尼材料的方法和笔者提出的多目标动力学拓扑优化方法设计车身敏感壁板阻尼层布局见图6。

计算求得两种车身阻尼材料布局对车内噪声影响效果见图7，车内118 Hz处异常噪声峰值大小见表3。

表3 118 Hz处车内噪声峰值Table 3 The peak value of noise in car at 118 Hz dB

图6 两种阻尼设计方法效果对比Fig. 6 Comparison of two damping design methods

图7 车内噪声改善效果Fig. 7 Interior noise improvement effect

通过车内噪声计算结果对比可知，两种车身壁板阻尼材料设计方案均使118 Hz处车内异常噪声峰值得到明显削弱。方案一使前、后排噪声测点在118 Hz处异常噪声峰值降低约4.5 dB，方案二使前、后排噪声测点在118 Hz处异常噪声峰值降低约6.6 dB。可见，方案二较方案一对车内异常噪声峰值控制具有更好的效果。

3.3 实车性能验证

为进一步验证上述阻尼材料设计方案对车内匀速噪声改善效果，开展实车100 km/h匀速工况车内噪声测试。在驾驶员右耳位置(DR测点)和后排座椅中间位置(RM测点)布置麦克风，通过LMS噪声测试系统采集到实车100 km/h匀速工况噪声数据见图8。

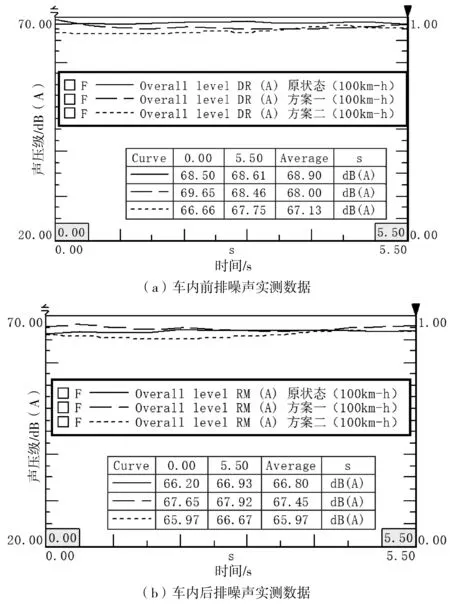
图8 车内噪声实测数据Fig. 8 Measured data of noise in car

通过100 km/h匀速状态下，车内噪声实测数据可知，方案一使前排噪声降低0.90 dB(A)，但后排噪声却升高0.6 5 dB(A)。而方案二使前排噪声降低1.77 dB(A)、后排噪声降低0.83 dB(A)。由此表明笔者提出的基于多目标动力学拓扑优化技术的阻尼材料设计方法对车内匀速噪声改善效果更佳。

4 结 语

针对某车型匀速噪声异常峰值控制，采用有限元仿真技术，根据车身壁板模态应变能分布和多目标动力学拓扑优化方法设计了两种阻尼材料设计方案。经仿真计算和实车测试结果表明，后者减振降噪效果更佳。

提出的阻尼材料设计方法充分考虑车身壁板与车内噪声的关联程度，获得的优化方案清晰，工程实施便捷，且具有良好的优化效果，可为同类车型车身阻尼材料总体布局设计提供思路借鉴和方案参考。