基于面曲率变化的模型桥损伤识别方法研究

张晓艳，汪富资，于 辉，吴 杰，唐 亮

(重庆交通大学 土木与工程学院，重庆 400074)

0 引 言

伴随着外部雨雪霜等环境侵蚀、桥梁结构自身材料老化及超载等不利因素的影响，桥梁主体结构会产生不同程度的损伤，刚度不断退化，最终导致突发性垮塌灾难。桥梁的坍塌事故具有突发性，严重威胁到人身和财产安全，故对桥梁进行经常性检查是非常有必要的。桥梁需要通过经常性安全检查，以发现桥梁结构损伤等问题，从而进行准确有效的维护，防止桥梁服务寿命低于计划期限。

在桥梁经常性检查中，实施方式普遍是通过人工进行桥面目视安全巡检。由于检测维护人员经验、数量的差异，其检测质量参差不齐。同时，人工检测不仅影响路面交通，而且其时效性也并不理想，更缺少量化依据对桥梁进行评估，往往需要从业人员以经验判断，也造成了桥梁检测结果的实际有效性低下。

针对量大面广区域范围内的桥梁，快速精确地进行变形检测，需要更有效准确的检测手段。地面三维激光扫描技术因具有常规测量手段不具备的自动化、进度高、非接触和测距远等优点，同时采用新的数据获取模式快速获取结构三维点云数据，在对数据进行相关分析处理后，能快速得到结构几何信息，因此基于三维激光扫描技术的非接触式自动检测系统可作为新的研究方向，解决现有桥梁检测难、精度差的问题[1]。

国内外对三维激光扫描的应用已非常广泛，在桥梁安全监测中的研究也是各出新意。徐健等[2]采用高速激光三维扫描和红外视觉成像法对老旧桥梁破损程度进行评估，仿真结果显示该方法对桥梁结构损伤点位置识别精度高，可靠性能较好，特别是针对20年以上的旧桥而言。王勋[3]利用徕卡Nova MS50三维激光扫描仪采集了桥面点云数据，识别出处于桥面平扫工况下3mm以上的桥面竖向挠度，该精度可用于柔性桥梁挠度观测及大跨径桥梁挠度观测。CHEN Xuexia等[4]利用车载激光扫描(VBLS)，并基于VBLS点的超高架桥主体特征提取与三维模型重建策略，建立起桥体三维曲面模型，证明了建桥模型的有效性和准确性。TANG Pingbo等[5]利用激光扫描点云中提取的测量目标，提出了一个用于构建和执行工作流程和机制的计算框架，使用3个度量工作流绩效定义了测量抽样穷举、测量目标结果的可靠性和时间效率。

在桥梁识别方面，国内外学者也应用各种方法对桥梁损伤情况进行评估。E.O’BRIEN等[6]研究了桥梁许多点基于偏转响应的损伤指标使用，当车辆穿过桥时，记录轴正下方偏转，创建移动参考偏转响应，然后可使用一批类似车辆的平均移动参考响应来产生损伤指标。Ö.E.AVSAR等[7]探究了激光跟踪技术在桥梁非接触变形监测中的应用，监测静态和温度负载下的桥梁变形。刘宇飞等[8]基于缺口平滑拟合技术研究了梁式桥梁在移动荷载工况下的损伤位置识别，利用整段桥上平均曲率模态变化值寻找桥梁损伤位置及程度，该方法为桥梁结构损伤位置识别提供了一种新的研究方向。

以上学者分别从挠度识别、变形检测、曲率模态方面进行桥梁识别。相较于已有较多研究的模态曲率这一动态方法来进行识别损伤[9-10]，笔者采用一种利用挠度曲线二阶微分得到曲率的静态识别方法。由于测量技术发展，特别是三维激光扫描和倾斜摄影三维建模方法的日益成熟，能在模型桥梁和实际桥梁上都可应用该技术精确找到桥面曲率变化值。笔者的研究重点为考察结构刚度减退(开裂)与桥面曲率的映射关系。为探寻基于桥面曲率变化的桥梁结构损伤识别，采用三维激光扫描获取桥面变形点云数据，通过分析桥面线曲率、面曲率变化来分析桥梁结构损伤情况。

笔者利用不同等级荷载损伤工况实现对T型有机玻璃模型梁桥的分析；同时基于三维激光扫描获取不同工况下的桥面几何点云数据，对比分析了在不同荷载作用下有机玻璃模型桥的挠度云图，依据实测三维点云数据进行损伤识别验证；然后对比3种代表工况下的桥面高斯曲率云图，基于桥面曲率在不同工况下的变化规律，为探索基于桥面曲率突变损伤识别方法在桥面变形监测应用提供参考。

1 有机玻璃模型桥面多级加载试验

1.1 实验目的

笔者探究了基于三维点云几何数据的桥面形态特征识别方法可行性；确定由结构损伤所引起的桥面挠度突变能否通过点云数据体现。通过设计一座简支梁T型有机玻璃模型桥，设置了多种不同等级荷载工况，并在边梁的跨中部位设置一条裂缝作为结构损伤。模型桥设置如图1。

图1 有机玻璃桥Fig. 1 Plexiglass bridge

1.2 模型桥设计相关参数

试验中设计模型桥为受力明确的简支T型梁桥，同时为使桥面挠度变形及结构损伤更为明显，该桥设计长宽比为B/L=0.5；其中桥长为1 600 mm，桥宽为800 mm。为使桥面变形显著同时减少桥面在加载时的覆盖范围，故采用基于杠杆原理的间接偏心加载，其加载如图2。加载过程中选取一根直径为30 mm的钢杆作为传力杠杆，通过轴承将杠杆一端和固定于地面上的支撑杆串联在一起，在相应的加载处重叠多个砝码当作钢杆的第二个支撑点，在钢杆的另一端悬置承台，通过增减砝码个数进行多级加载。当加载时，在钢杆一端放置一枚砝码，则荷载可通过杠杆传达到模型桥面，单个砝码的重量为2 kg，荷载分3个级别加到模型上。具体荷载分级工况为：1级为14 kg，2级为28 kg，3级为42 kg。

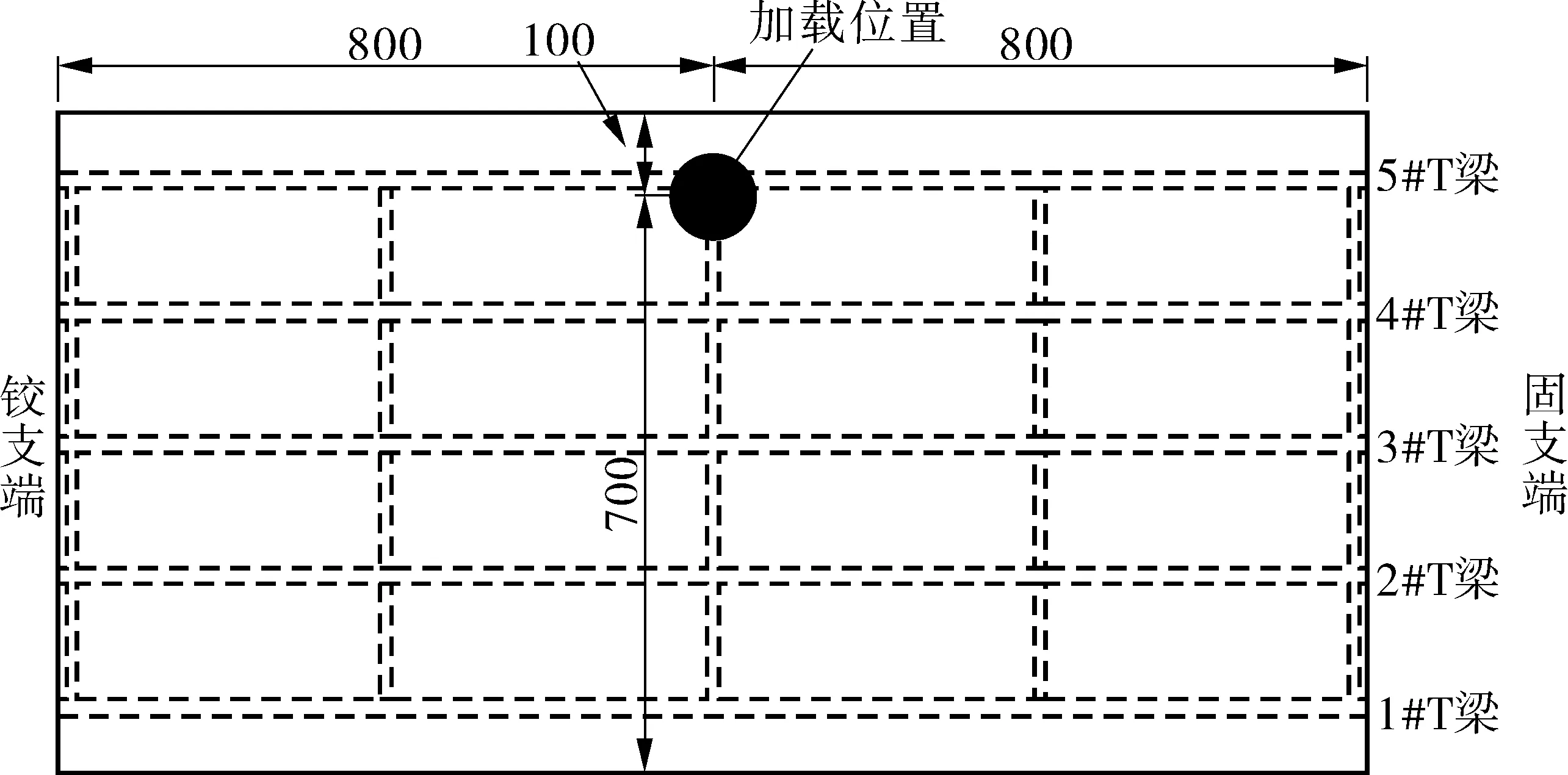
图2 简支T型梁桥加载位置示意Fig. 2 Schematic diagram of loading position of simply supported T-beam bridge

为分析桥梁结构损伤产生的桥面形变及三维激光扫描对于桥面形变测量的可行性，故在完成对于有机玻璃T型梁桥的无损伤工况加载测量后，人为设置桥面损伤使之成为有损模型梁桥，加载后再进行桥面的三维激光扫描测量。本次试验中选择位于第5片T梁肋板底设置宽度为0.6 mm、高度为80 mm的裂缝，使得有机玻璃模型梁桥的桥面挠度更为明显，如图3。

图3 裂缝示意Fig. 3 Sketch map of the crack

1.3 位移计测量数据与桥面三维点云数据对比

实验选择三维扫描系统(徕卡Nova Ms50)对桥面形态数据进行采集。为准确地将有损简支梁T型模型桥及无损简支梁T型模型桥在不同加载工况下的桥面竖向形态变化进行比较，笔者选择使用Geomagic Qualify的3D比较功能对已进行去噪处理的三维点云数据进行分析，从而得到基于不同荷载工况下的桥面竖向形态变化云图。

图4为3级荷载作用下的无损伤简支梁T型桥的桥面点云与无荷载时桥面初始点云的对比云图，以向上作为正，向下作为负。

图4 无损伤简支T型梁桥3级荷载作用下挠度云图(单位：m)Fig. 4 Deflection nephogram of simply supported T-beam bridgeunder three-stage load without damage

2 曲率突变的损伤识别法及桥面曲率变化分析

2.1 突变曲率的损伤识别法

在对模型桥面三维点云数据特征面的分析中，笔者主要提取了桥面高斯曲率和特征面的挠度曲率，同时利用曲率突变损伤识别法对数据进行处理和分析。

基于虚功原理，梁式结构中任意点的挠度[11]可用式(1)表示：

(1)

由于桥梁结构大多为受弯结构，其轴向变形和剪切变形相对于弯曲变形可忽略不计，因此在不考虑构件的剪力和轴力变形后其挠度表达如式(2)：

(2)

由图5中挠度关系可知，桥梁结构的挠度曲线普通方程如式(3)：

y=f(x)

(3)

式中：x为沿着梁长度方向的坐标；y为梁的曲率。

图5 挠度关系示意Fig. 5 Schematic diagram of deflection

同时，挠度曲线的曲率如式(4)：

(4)

式中：ρ(x)为曲率半径。

忽略式(4)中的高阶项，可得挠度曲线曲率近似公式如式(5)：

(5)

梁中任意截面处弯矩与挠度的关系如式(6)：

(6)

式中：E为梁的弹性模量；I为梁截面惯性矩；M(x)为作用梁上的荷载产生的弯矩。

将式(5)带入式(6)中可得到：梁中任意截面的弯矩、刚度及挠度这3者之间关系如式(7)：

(7)

综上可知：当梁中未出现结构性损伤或荷载和结构类型未变化时，截面挠度和挠度曲线曲率呈正相关；相反，出现结构性损伤的梁截面位置处刚度会有一定削弱，在损伤部位处的挠度值和挠度曲率值将会发生突变。因此可基于梁中截面挠度值或挠度曲率值是否发生突变来对桥梁结构损伤进行判断，即通过桥梁结构的桥面形态数据来推断桥梁结构中是否有明显的结构性损伤[12]。

2.2 基于高斯曲率的损伤识别法

受弯薄板的挠度微分方程如式(8)：

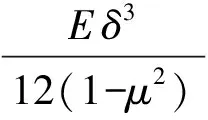
(8)

或表示如式(9)：

D4w=q

(9)

弹性薄板X与Y方向的曲率和扭率如式(10)：

(10)

式中：1/rx、1/ry、1/rxy分别为X、Y方向的曲率和XY平面的扭率。

当τxy=0时，1/rxy=0，即X、Y轴为主应力方向，同时也是主曲率方向。亦即，在弹性薄板中，一点的主应力方向与主曲率方向相同，如式(11)。

(11)

κ1=1/r1，κ2=1/r2，其中：κ1、κ2分别为最大和最小主曲率。则高斯曲率K定义如式(12)：

K=κ1×κ2

(12)

高斯曲率与薄板的抗弯刚度有一定关系。因此，在接下来研究中，笔者采用高斯曲率法用于评估结构损伤引起的刚度退化。

2.3 特征截面挠度与挠度曲率对比

模拟三维点云数据，并进行对比分析，建立起简支T型有机玻璃试验桥的有限元模型。将其网格化为较细的微小单元体，模型分析时先考虑自重作用下对桥面形态变化影响。

建立有限元数据模型，并提取有限元模型上特征面1在有损伤和无损伤情况下的桥梁特征截面挠度及挠度曲率。特征截面1、2设置如图6。根据有限元数据模型，对比基于有损伤工况荷载下三维扫描点云和有限元模型位于特征截面1处的挠度及挠度曲率，如图7。

由图7可知：三维扫描点云和有限元模型位于特征截面1处的挠度及挠度曲率曲线走向大致相同，但其特征截面的挠度曲率曲线存在一定偏差；同时在结构损伤位置附近均出现了明显峰值，且峰值基本相同；点云数据与有限元数据在有损伤结构桥面曲率峰值位置有一定偏差，但两者峰值位置均出现在损伤区域附近，因此仍可用该方法大致确定损伤位置。

图6 有限元模型中特征点、特征截面示意Fig. 6 Schematic diagram of feature points and feature sections inthe finite element model

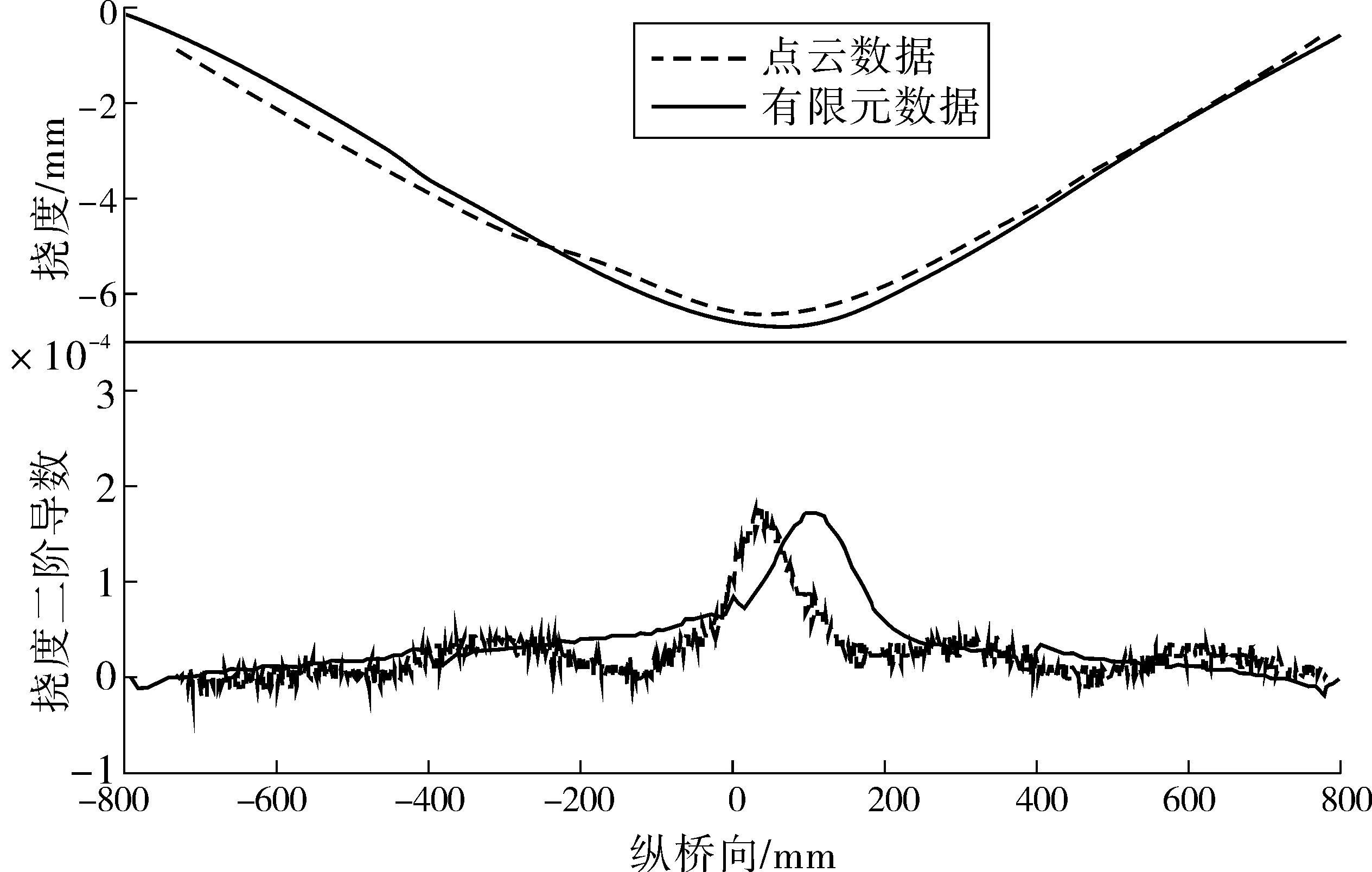
图7 有损伤点云数据和有限元数据中特征截面1的挠度及挠度曲率曲线Fig. 7 Deflection and deflection curvature curve of characteristicsection 1 in the damaged point cloud data and finite element data

2.4 利用桥面高斯曲率进行损伤识别

2.4.1 边主梁不同开裂位置下桥面高斯曲率

由于简支梁桥结构中不同位置相同损伤处会发生相应的刚度退化，故梁中不同位置病害所在截面的挠度值和挠度曲率值将会发生不同程度突变。在有限元模型中5#边梁1/2截面与1/4截面处分别设置相同的裂缝，计算时仅考虑自重作用，计算出不同工况下桥面各点的高斯曲率值，从而得到桥面高斯曲率云图。

由于简支梁横隔板存在，使得裂缝设置并不方便，所以边梁上的两处裂缝不能正好落在其1/2、1/4截面位置，而应该分别设置于1/2、1/4截面偏右侧17.5 mm位置，从而避开了此区域。计算三维点云数据的高斯曲率值，将每一个点对应的高斯曲率值拟合成整个桥面的高斯曲率云图，然后把相同位置处有限元所提取的挠度云图和桥面高斯曲率云图相互对应，如图8、 9。

无论是1/2截面还是1/4截面处设置开裂，在有限元模型同程度损伤设置的不同位置，桥面高斯曲率在对应部位均发生了曲率突变，云图出现了部分凸起，伴随着相应的高斯曲率最大值和最小值。对比在不同位置设置的同程度损伤给高斯曲率云图带来的不同影响发现：随着开裂位置由跨中向支座位置移动，损伤造成的挠度曲率突变逐渐弱化，凸起处高斯曲率最大、小值的绝对值也逐渐减小。

图8 开裂工况下挠度云图Fig. 8 Deflection nephogram under splitting conditions

图9 开裂工况下高斯曲率云图Fig. 9 Gaussian curvature nephogram under splitting condition

2.4.2 边主梁不同开裂数量下桥面高斯曲率

在简支梁桥中，考虑到当结构出现不同数量同程度的损伤时，结构在相应损伤位置会出现不同刚度的退化[13]。桥面在不同数量同程度损伤下，对应截面处挠度值和挠度曲率值将会发生不同程度的突变。在有限元模型中5#边梁设置3个同程度不同位置的裂缝，分别位于1/2截面和其左右200 mm处，只考虑自重作用，估算整个桥面高斯曲率。

桥面高斯曲率云图出现了3处凸起，且凸起数量与边梁设置裂缝个数相同。由于3个不同位置所设置同程度损伤与先前一个位置处所设损伤相同，因此可对比分析图9、11中的高斯曲率云图。由两幅图的对比可知：结构的桥面曲率在结构损伤位置处出现了峰值，同时其峰值数量随着损伤数量增加而增多，由于多处裂缝之间相互影响，致使高斯曲率的最大、小值出现了一定弱化。

图10 3处损伤工况下挠度云图Fig. 10 Deflection nephogram under three damage conditions

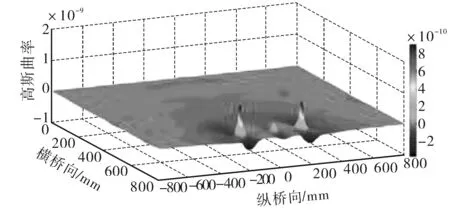
图11 3处损伤工况下高斯曲率云图Fig. 11 Gaussian curvature nephogram under three damage conditions

2.4.3 有限元与点云数据桥面高斯曲率对比

由有限元模拟结果可以看到：通过三维点云数据提取同一位置特征面挠度值基本与有限元数据模型所提取的相符。通过挠度曲率突变的峰值点可以大致确定损伤位置。

为了进一步分析桥面变形情况，笔者针对有机玻璃模型桥中最具代表性的两种工况，将有限元数据模型与三维点云数据所拟合的高斯面曲率进行对比分析。两种工况分别为：无损伤空载、有损伤满载。估算出不同工况下三维扫描点云的数据高斯曲率值，通过MATLAB将每个点对应的高斯曲率值拟合形成完整曲面，从而得到两种工况下有限元数据与点云数据提取的对比高斯曲章云图，如图12～14。

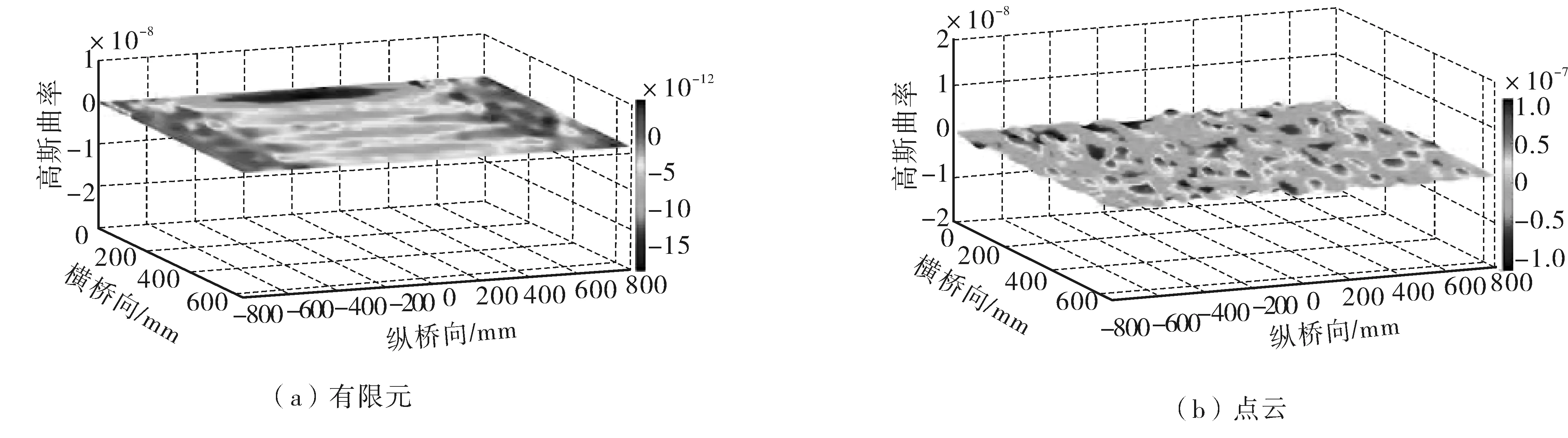
图12 模型桥提取的无损伤空载高斯曲率云图Fig. 12 Non-damaged no-load Gaussian curvature nephogram extracted from model bridge

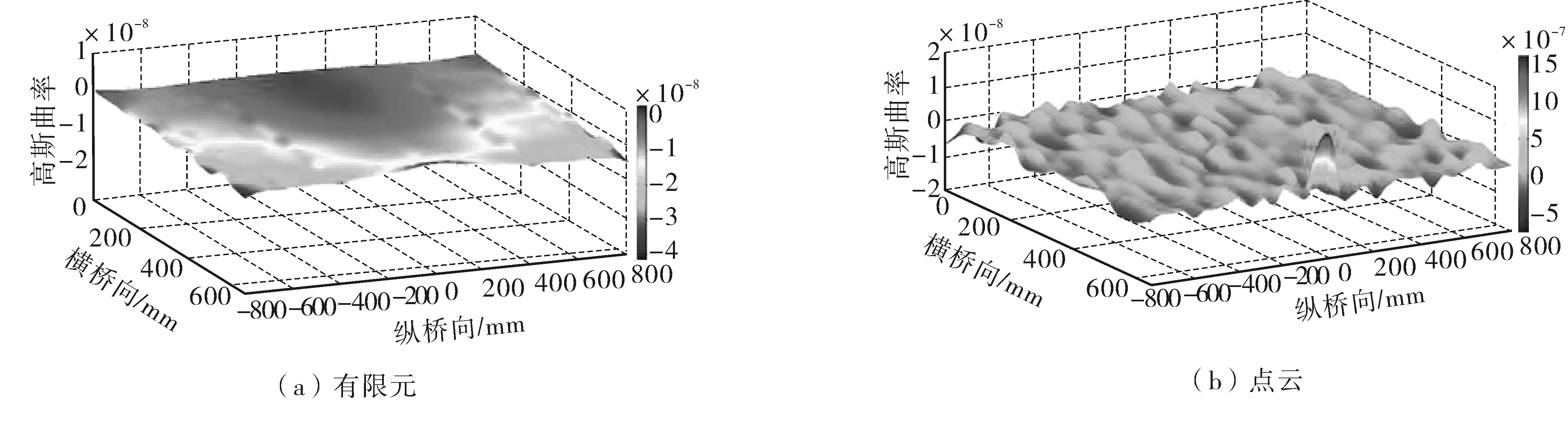
图13 模型桥提取的无损伤满载高斯曲率云图Fig. 13 Non-damaged full-load Gaussian curvature nephogram extracted from model bridge

图14 模型桥提取的有损伤满载高斯曲率云图Fig. 14 Damaged full-load Gaussian nephogram extracted from model bridge

当有限元模型处于空载时，结构主要由支座部位和各主梁承载。点云数据桥面高斯曲率云图呈现凹凸不平形态，试验因T型有机玻璃桥材质为无色透明，对光反射率较低，影响三维扫描采集效果，因此于桥面贴置不透明白色贴纸，气泡的存在致使桥面出现轻微的凹凸不平，可模拟实际桥梁中桥面铺装破损造成的桥面凹凸不平。

由有机玻璃桥面高斯曲率云图〔图12(b)〕可知：模型桥在无损伤空载作用下时的桥面初始状态为平面，且高斯曲率值较小，其变化范围在-1E-7～1E-7之间波动，相对于无损伤满载和有损伤满载的高斯曲率云图波动范围小。由图〔图13(b)〕可知：模型梁桥在无损伤满载工况下的高斯曲率云图向上峰值较大，同时基于MATLAB中的Data Cursor功能分析，以(800, 0)为中心坐标，30 mm为半径的加载点范围内所获得的高斯曲率最大值所对应坐标为(650, -25)；模型梁桥在无损伤满载工况下的高斯曲率云图向下峰值较大，重复Data Cursor功能分析可获得凹陷最低点的坐标值分别为(650, 135)，对照加载点坐标范围和开裂损伤对应桥面坐标可判断为是由开裂损伤引起。

从有损伤满载的高斯曲率云图中可发现：此时有限元数据提取的高斯曲率云图出现了下凹，并且凹陷部位最低点位于对应损伤位置附近；点云数据提取的高斯曲率云图也出现了下凹，参照加载位置的坐标范围以及桥面设置裂缝位置坐标，可确定是由结构开裂损伤引起。这些现象和规律可为将来通过桥面高斯曲率变化规律识别结构损伤提供参考[14-17]。

3 结 论

笔者利用实验室自制的一座有机玻璃模型梁桥，通过三维激光扫描技术获得桥面点云数据，基于桥面高斯曲率分析方法对桥梁结构损伤识别进行了探索，得到如下结论：

1)通过对比分析三维点云数据和有限元模型位于特征截面1处的挠度及挠度曲率曲线图形，发现两者曲线走向大致相同，但其特征截面的挠度曲率曲线存在一定偏差；同时在结构损伤位置附近均出现了明显峰值，且峰值基本相同；但这两者峰值位置均出现在损伤区域附近，通过该方法可大致确定损伤位置；

2)将有限元数据模型与三维点云数据所拟合的桥面高斯曲率进行对比分析也可得到类似的结论：无损空载时，高斯曲率值波动较小，两种曲率云图近似于平面，无异常凸起点；有损满载时，有限元数据提取的高斯曲率云图出现了下凹，且凹陷部位最低点位于对应损伤位置附近；

3)考虑到边主梁不同开裂数量下桥面高斯曲率的变化规律：当设置3个同程度不同部位损伤时，发现桥面出现3处凸起，且凸起数量与边梁设置裂缝个数相同；随着损伤数量增加，高斯曲率突变也相应增加，但由于多处裂缝之间相互影响，致使高斯曲率最大、最小值出现了一定弱化；

4)桥面高斯曲率相对于挠度对损伤更敏感，通过桥面高斯曲率变化规律可识别结构损伤的数量、位置和程度等特征。同时研究发现：不仅是桥梁结构刚度损伤会引起桥面几何形态改变，桥面铺装随营运时间增加所引起的老化损坏、环境温度变化等情况也会带来改变。因此，需要将这些因素剔除，保留由于结构老化损伤引起的桥面形态变化量，从而为安全状态监测与预警提供准确基础数据。桥面点云数据采集噪声信息主要是测量环境的温差效应和桥面局部破损，环境温差效应对桥梁结构带来影响主要是整体位移及应力[18]。

5)接下来的研究中，笔者拟在实测桥梁上针对性设置温度测点，通过高频次车载三维激光扫描系统采集桥面形态点云数据，提取日温差和日温差变形效应，建立日温差特征趋势模板，选取适当的数学预测模型实现基于复现频率的日温差模板外推年温差，从而分离日/年温差变形效应因素；拟通过数值模拟分析桥梁承重结构刚度变化引起的桥面形态变化形状特征，建立起典型桥面形态变化特征尺寸和形状模板，提取实测桥面形态变化参数特征，将桥梁结构刚度变化等带来的桥面形态变化和因铺装自身原因引起的局部破损进行特征分类判别，以达到分离桥面铺装局部破损噪声信息目的。