基于相互作用矩阵法的灾变系统多因素复杂关系研究

姚令侃，张孟帅，黄艺丹，孙少伟

(1.西南交通大学 土木工程学院，四川 成都 610031；2.高速铁路线路工程教育部重点实验室，四川 成都 610031；3.陆地交通地质灾害防治技术国家工程实验室，四川 成都 610031)

0 引 言

2018年10月11日凌晨，四川省甘孜藏族自治州白玉县境内发生了山体滑坡，致使金沙江干流堵塞，形成堰塞湖；2018年10月17日，西藏自治区林芝市米林县发生了雅鲁藏布江滑坡堵江，形成堰塞湖。这类灾害对自然环境和人类社会造成了极其严重的损害。复杂灾害影响因素众多，各因素之间除了存在因果关系外，还可能存在相互作用关系，这给灾害机理的研究带来了很大困难。并且，具有因果关系的一系列灾害相继发生，使得灾害模式复杂、灾势时空放大，导致探究灾害形成机理的科研活动难以展开[1]。

对灾变过程和灾变系统因素间相互作用关系的研究已成为具有重大理论意义和实践价值的课题。史培军[2]将灾变系统的研究归纳为4种理论，即：致灾因子论、孕灾环境论、承灾体论和区域灾害系统论，这些理论从诱因、环境及承载体等方面对灾害进行了分析；李夕兵等[3]通过对汛期尾矿坝溃坝事故的分析，构建了尾矿坝溃坝的事故树图，形象直观地反映了事故成因及逻辑关系；李凡等[4]对含硫油品储罐自燃事故中的“人-机-料-法-环”因素进行了详细分析，构建了鱼刺图，条理清晰地展示了储罐自燃事故各因素之间的逻辑关系；裘江南等[5]构建了突发事件贝叶斯网络，描述了突发事件的发展过程，并对事件进行了预测和诊断。迄今，科研人员已经对灾变系统因素组成的框架、层次及因果关系进行了深入研究，但关于灾害因素相互作用关系的研究鲜见报道。笔者应用事故树分析法、解释结构模型法和相互作用矩阵法等3种数学方法，分析了灾变系统多因素复杂关系，并以八渡车站多级滑坡为例，揭示了灾害的形成过程及发展路径，制定出合理的灾害风险控制对策。

1 灾变系统形成过程分析——事故树法

笔者选择八渡车站多级滑坡的形成过程进行分析，采用事故树法描述主级滑坡和次级滑坡的事故树图，探究各滑坡子系统之间的关系。

1.1 八渡车站滑坡简介

南昆线八渡车站位于贵州省黔西南布依族苗族自治州册亨县八渡镇的南盘江左岸斜坡上，该地区属于中低山峡谷陡坡区，应力相对集中，常年降水充足。八渡车站滑坡是由3个山头组成的巨型深层、切层古滑坡，周界清晰，前缘向南盘江突出，后缘轮廓呈圈椅状，如图1。滑坡体总长约700 m，宽约360 m，坡体为上部凹陷，下部突出的台阶状外貌[6-8]。

图1 八渡车站滑坡全貌Fig. 1 Landslide at Badu railway station

滑坡分为主、次两级(线路左侧为主级滑坡，右侧为次级滑坡)，如图2。该古滑坡原处于稳定状态，由于受到以下因素影响，滑坡出现复活迹象：

1)线路施工对滑坡进行大开挖而形成高陡边坡，使次级滑坡在坡脚形成临空面，并且挖方弃土直接堆积在主级滑坡下滑段上，导致主级滑坡下滑力增大。

2)在滑坡体上修建构筑物及当地居民生活废水的随意排放，均降低了坡体的稳定性。

3)连续集中的降雨致使滑坡体内渗入大量雨水，造成坡体滑动带软化及土层软弱，降低了土体的抗剪强度，增大了坡体重量[7,9]。

图2 滑坡分布剖面Fig. 2 Landslide profile

1.2 八渡车站滑坡灾害成因的事故树法分析

事故树法是按人的思维方式，由结果去推导可能造成事故原因的分析方法[10-11]。通过分析顶上事件(即事故事件)，依据相关事故发生时的资料和事件内部各因素之间的相互关系，得到造成事故的直接原因和间接原因。

笔者结合相关资料，分别编制出主级滑坡复活和次级滑坡复活2个事故的事故树图，如图3。

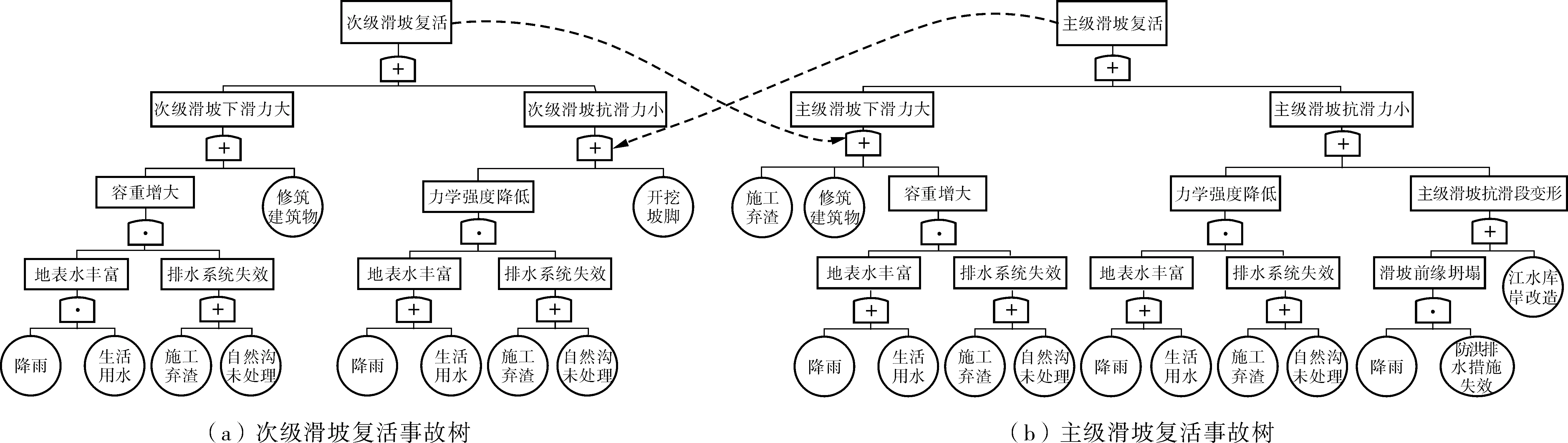
图3 事故树Fig. 3 Accident tree

出现滑动的主级滑坡会对次级滑坡形成牵引，致使次级滑坡滑动；若次级滑坡发生滑动则会在主级滑坡坡体上形成堆载，加剧主级滑坡的滑动。图3中的虚线描述了两者之间的相互影响关系。此时各因素之间的层级关系相对混乱，已无法用事故树图进行描述。

当逻辑关系不明确、组织结构混乱时，研究者无法通过常规分析得出结构图，此时可利用解释结构模型法来分析整理多因素影响关系[12-14]。

2 灾变系统分析——解释结构模型法

2.1 解释结构模型法的原理

2.1.1 通过已知图形关系构建邻接矩阵A

根据系统因素间有向关系图构建邻接矩阵A。若因素间有直接联系，则在邻接矩阵中用数值“1”表示；若因素间无直接联系，则用数值“0”表示。这样即可构建一个反映各因素间关系的邻接矩阵A。

假设系统S有n个单元，即：

S=[S1,S2,…,Sn]

则，系统S的邻接矩阵A为

S1S2…Sn

(1)

2.1.2 通过布尔运算计算可达矩阵M

M=I∪A2∪A3∪…∪An=(I∪A)n

(2)

2.1.3 对可达矩阵M进行分析

找出可达矩阵M中的特色因素，进行区域划分，在此基础上再进行层次划分。

2.1.4 提取骨架矩阵M″

1)去除强连接因素得到浓缩矩阵M′。在系统中，任意两个单元在可达矩阵M中的行值和列值完全相等，则将其视为一个系统单元，从而可对相应的行和列进行化简，得到新的可达性矩阵，称做M的浓缩矩阵M′。

2)去除越级二元关系。

3)去除单位矩阵得到骨架矩阵M″。

2.1.5 绘制多级递阶有向图

1)从上到下按照不同区域逐级排列系统构成因素。

2)加入同层中所删除的与某因素有强连接关系的因素，同时加入反映它们间相互关系的有向弧。

3)根据骨架矩阵M″所反映的邻接二元关系，用级间有向弧将其连接构成有向图。

2.2 复杂灾害系统的解释结构模型法分析

依据事故树图中所反映的各因素间连接关系构建邻接矩阵A，并遵循2个规则：①保留事故树中所有影响因素；②在构建邻接矩阵时，分别用数值1、0表示因素间有、无影响。八渡车站两级滑坡系统所涉及的20个主要影响因素见表1。根据表1因素之间的关系构建邻接矩阵A，如图4。

表1 滑坡致灾因素的可达集、先行集和交集Table 1 Reachability set, the first set and the intersection set of landslide causes

图4 邻接矩阵AFig. 4 Adjacency matrix A

利用式(1)进行可达矩阵计算，经过5次布尔运算后得到稳定的可达矩阵M，如图5。

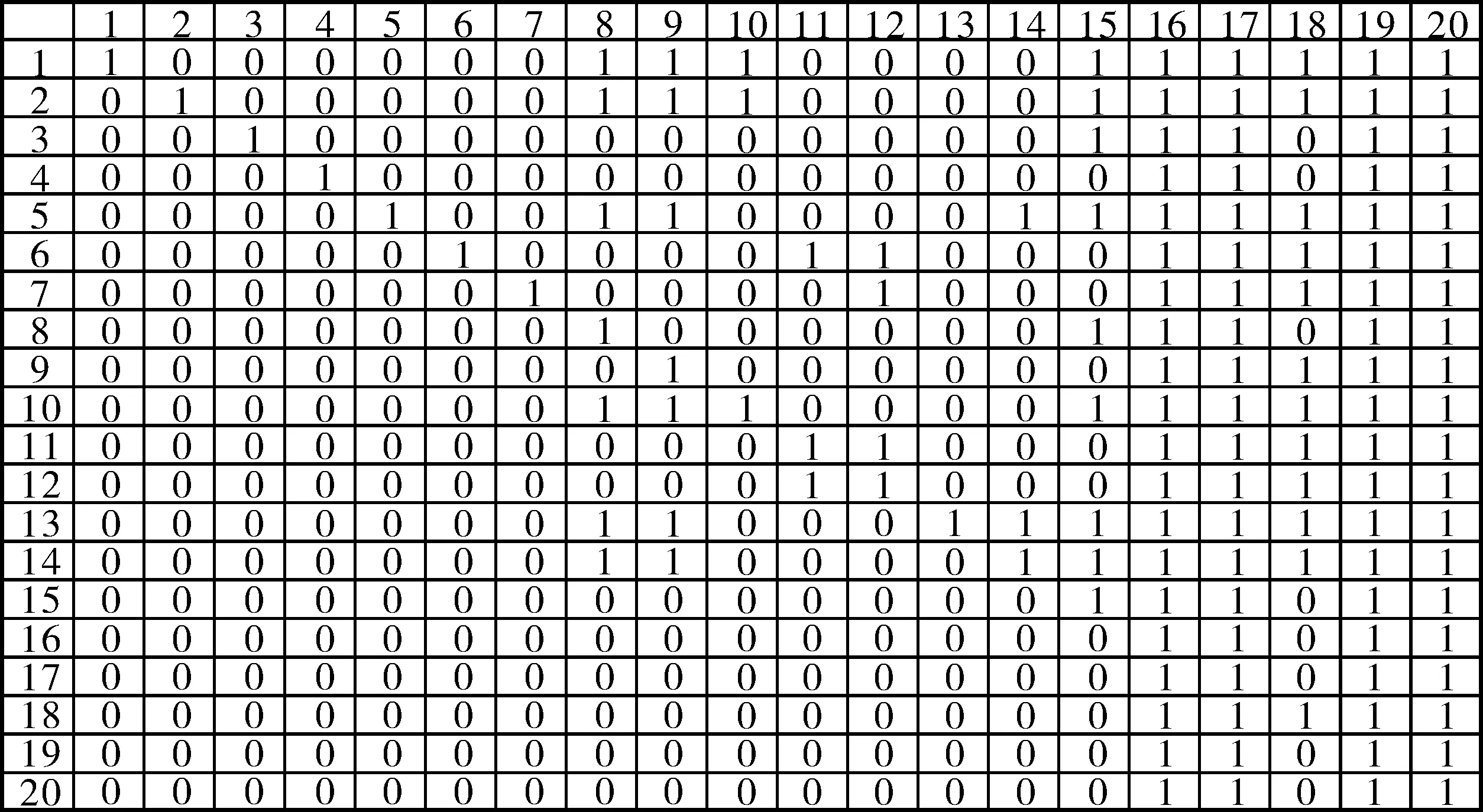
图5 可达矩阵MFig. 5 Reachability matrix M

对可达矩阵M进行分解，得到每个因素的可达集和先行集，进而求得其交集和层数，数据整理结果见表1。

在可达矩阵M中，发现在第1层4个节点因素中，相应的行、列元素值分别完全相等，说明这4个节点构成回路集，其中任意一个节点即可代表回路集中的其他节点。因此，去除可达矩阵M中这4个因素中的3个，得到浓缩矩阵M′(图6)，从而简化了相互作用这一复杂过程。

去除浓缩矩阵M′中的越级二元关系，同时减去单位矩阵，得到骨架矩阵M″，如图7。

图6 浓缩矩阵 M′Fig. 6 Concentration matrix M′

骨架矩阵M″反映了系统的多级层次结构，以此绘制影响滑坡系统的多因素、多级递阶结构图。由于顶层4个因素可视为等价因素，为了更清晰地表示出顶层因素之间的逻辑关系，对该层4个因素进行分析得到影响滑坡系统主要因素的多级递阶结构，如图8。

图7 骨架矩阵M″Fig. 7 Skeleton matrix M″

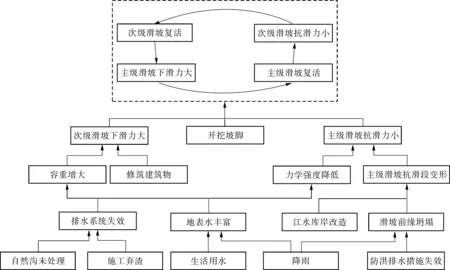
图8 滑坡系统主要因素的多级递阶结构Fig. 8 Multi-level hierarchical structure diagram of major causes for landslides

图8中，虚线方框内的循环路径描述了顶层4个节点构成的回路集，其中任何1个因素的改变都会对另外3个因素产生较大影响。通过层级分解，多级递阶结构图将各因素划分为不同层级，用以描述同一层级之间内部的相互作用关系，对于同一因素的不同路径影响进行简化，因而，图形结构更加清晰、层次分明。

事故树图无法表征八渡车站复杂滑坡系统成因、无法确定各个因素所属层级，而多级递阶结构图则可以解决这些问题。与图3相比，图8简洁、层次分明、条理清晰，由上而下显示出了一种递阶的控制作用关系。

事故树法和解释结构模型法侧重于描述滑坡系统各因素之间的层次关系和因果关系，但对于多级滑坡组成的大型滑坡，由于各级滑坡之间存在相互作用，即一种互为因果的特殊关系，若想对这种相互作用关系进行定量分析，则需要另辟途径。同时，在工程建设中，若视灾害为环境，则灾害危及的工程对象也可能会存在与环境相互作用问题，如大型交通土建工程建设对环境演变造成的影响，加速了环境恶化，引发或加剧了自然灾害而反作用于工程建筑本身。据统计，世界上超过75%以上的滑坡灾害都与人类活动有关，我国因修建铁路形成的泥石流沟就有174条[15]。工程与环境之间的相互作用机制是目前国际上倍受关注且尚未突破的学科前沿问题，也是我国环境脆弱山区道路建设急待解决的关键科学技术问题。

3 八渡车站滑坡选线策略——相互作用矩阵法

3.1 相互作用矩阵法的原理

相互作用矩阵法由J. A. HUDSON[16]提出，用以研究岩石工程系统，其基本思想是通过分析构造与系统相关的多因素作用矩阵，编码并进行定量评价。在相互作用矩阵法中，主对角线对应各研究因素，非对角线为对应因素之间的影响值，如图9。该方法通过矩阵运算可定量获得因素对系统、系统对因素之间作用强度的信息，特别适合用来解决多因素之间的相互作用和相互耦合等复杂情况[13,17]。

图9 多因素相互作用矩阵Fig. 9 Multi-factor interaction matrix

3.2 相互作用矩阵的建立

选取因素P1代表主级滑坡子系统，P2代表次级滑坡子系统，P3代表线路工程子系统。3个因素之间相互影响关系如图10。

根据八渡车站线路情况，选取以下3种不同位置方案(图11)：

方案Ⅰ：线路以路堤形式通过次级滑坡坡脚；

方案Ⅱ：线路以路堑形式通过次级滑坡坡脚；

方案Ⅲ：线路以路堑形式通过次级滑坡坡顶。

采用专家半定量法[16]对矩阵进行编码，利用相关函数关系或专家经验将作用强度进一步细分，进而完成编码工作。具体的编码规则：“-2”为不利相互作用；“-1”为弱不利相互作用；“0”为无相互作用；“1”为弱有利相互作用；“2”为有利相互作用。

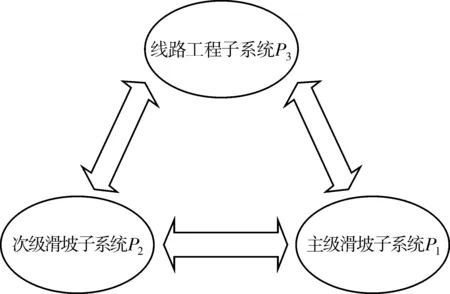
图10 各子系统间相互作用示意Fig. 10 Interaction between various subsystems

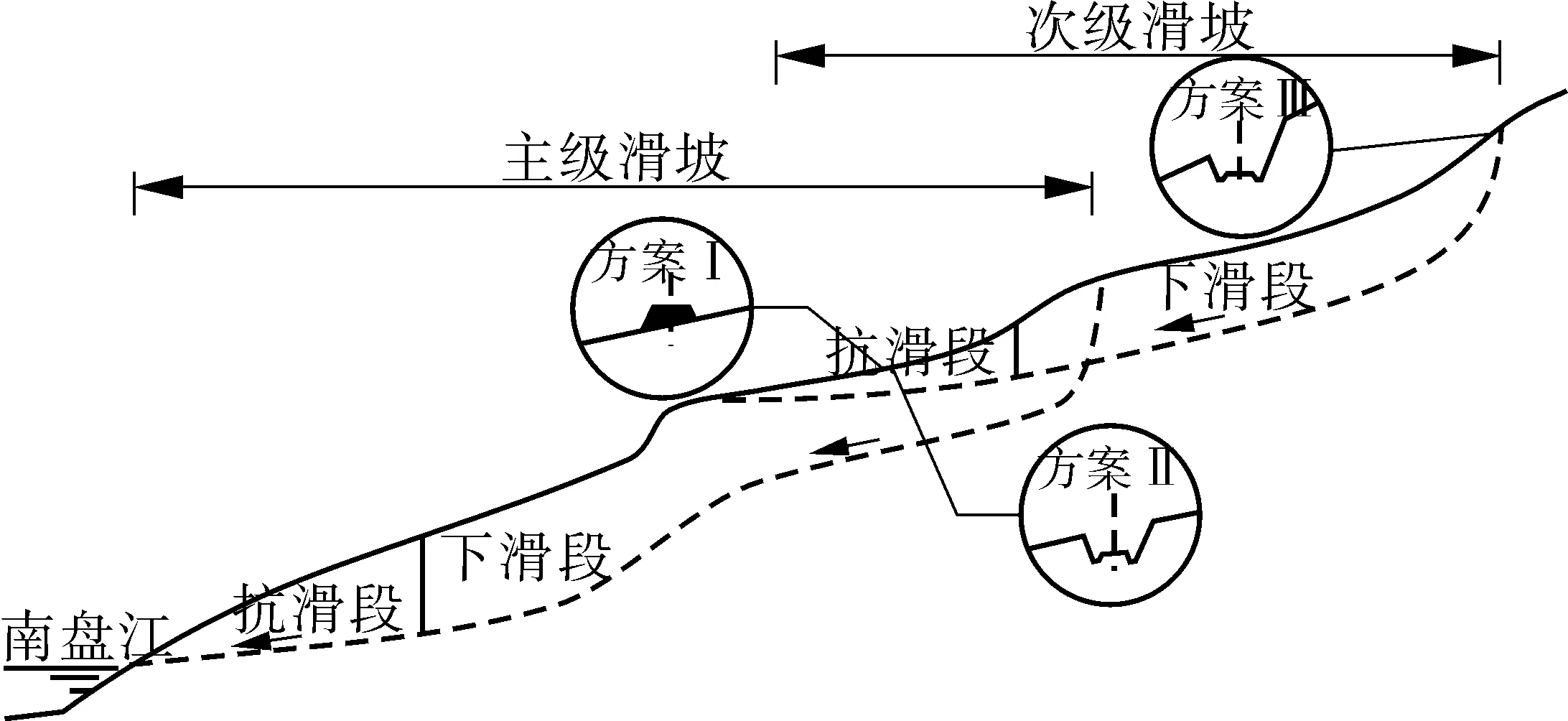
图11 线路选线方案Fig. 11 Route selection schemes

依据相互作用矩阵原理，笔者建立起3个方案的相互作用矩阵如表2，将P1(主级滑坡子系统)、P2(次级滑坡子系统)、P3(线路工程子系统)依次填入各方案作用矩阵的主对角线位置，然后按照顺时针方向对非对角线位置进行编码，例如：X12=“-2”，表示P1对P2有不利作用。

表2 3个方案的相互作用矩阵Table 2 Interaction matrix of the three schemes

3.3 基于相互作用矩阵的方案比选

在每个相互作用矩阵中，行值之和表示因素对系统的影响强度，列值之和表示系统对因素的作用强度，行值和与列值和相加为该因素的相互作用强度。方案Ⅰ、方案Ⅱ、方案Ⅲ的作用强度计算结果分别为：-3、-5、-1。

作用强度值为正时，其值越大，方案越优；作用强度值为负时，其值越小，方案相对劣势值越大，方案越不利。3个方案的总作用强度值均为负值，说明这3个方案均属劣势方案，劣势强度从大到小排序为：方案Ⅲ > 方案Ⅰ> 方案Ⅱ，说明从次级滑坡坡顶以路堑形式通过滑坡区的方案相对最优。

3.4 基于成灾路径分析施工方案风险控制

在相互作用矩阵中，非对角项表示两个因素之间的影响关系。当选取3个或3个以上因素进行分析时，它们的相互作用关系可用一条穿梭于矩阵中的路径来表示[16-17]。通过路径分析可得到该路径强度，依据强度值判断系统机制回路为正反馈机制还是负反馈机制，然后找出该路径的关键节点，从而可针对性地进行风险控制。

3.4.1 案例分析

方案Ⅱ为线路以路堑形式通过次级滑坡坡脚。路堑施工会使次级滑坡坡脚形成临空面，但可减轻主级滑坡上部荷载，反过来主级滑坡和次级滑坡也会作用于线路工程。若从方案子系统P3出发，通过一定路线最终又回到方案子系统P3，可找到4条主要路径，如图12。

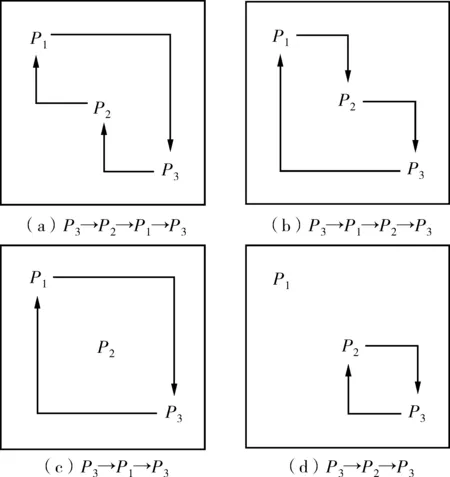
图12 方案Ⅱ成灾路径Fig. 12 Disaster path of scheme-Ⅱ

成灾路径的强度值为负，表示成灾路径为正反馈，可增强系统中的扰动，强度值越小，沿该路径发生灾害的可能性就越大；成灾路径的强度值为正，表示成灾路径为负反馈，可减少系统中的扰动，强度值越大，路径越有利。表3为方案Ⅱ的路径强度值。

表3 方案Ⅱ路径强度Table 3 Path intensity of scheme-Ⅱ

由表3可见，方案Ⅱ中的4条路径强度值均为负值，表明每条路径都会产生正反馈，增强扰动。其中，第1、4条成灾路径的强度值相对更小。第1条成灾路径表示线路施工会使次级滑坡坡脚形成临空面，反过来次级滑坡滑动又会影响到主级滑坡，最终对线路工程产生不利影响，说明在此链式反应过程中，次级滑坡失稳是源头事件；第4条成灾路径表示线路开挖影响到次级滑坡，次级滑坡又反作用于线路工程，产生极其不利的影响，说明次级滑坡失稳也是源头事件。

综上，方案Ⅱ开挖坡脚导致次级滑坡失稳是源头灾害。因此，当确定方案Ⅱ为施工方案时，重点要防止次级滑坡失稳，可制定预先支护后开挖的施工方案，以减少施工引发滑坡灾害的风险。

3.4.2 评价结果

南昆铁路在八渡车站滑坡处实际采用的是方案Ⅱ，即以路堑形式通过次级滑坡坡脚，这是当时投资最小的方案。但在施工过程中，出现了右侧边坡护坡工程鼓胀开裂甚至抗滑桩倾斜等坡体明显失稳征兆。后经设计单位复查，判定主级滑坡为相对稳定的古滑坡，次级滑坡为线路工程开挖引起的工程滑坡，若不治理，不但直接影响到线路工程，还可能导致主级滑坡复活。因此，先后设置3排76根抗滑桩并修建了大量的地面、地下截排水工程对次级滑坡进行治理，增加的滑坡治理费用超过9 000万元[9,18]。结果表明，从工程经济角度考量，方案Ⅱ也不合理。可以说，对滑坡复杂关系定量分析方法的缺失，也是造成施工扰动导致边坡演变成滑坡或老滑坡复活事故多发的原因之一。

4 结 论

1)事故树图是描述灾害系统的基本工具，可以清晰地描述导致灾变事件发生的过程及因果关系。在较复杂的情况下，解释结构模型法通过层级分解和断链将复杂关系简洁化、层次化、条理化，以由上而下的递阶方式反映因素间的控制作用，不过，使用该方法的前提条件是能够准确建立起反映各因素连接关系的邻接矩阵。当灾害系统因素多、因素之间关系模糊时，可先利用解释结构模型法理清因素间的层级关系，即确定其中某部分的逻辑关系，再利用事故树法分析各因素之间具体的因果关系。这两种方法均属于用图形描述灾害过程，二者配合使用效果较显著。

2)相互作用矩阵法是分析系统各因素间相互作用关系和量化评估它们相对重要性的方法。根据相互作用矩阵原理，通过分析工程和环境这两个不同属性系统之间相互耦合作用关系，可对线路方案进行比选。该方法存在着更广阔的应用拓展空间。