基于量纲分析的优化神经网络模型预测GAGD非混相开发油藏采收率

陈小龙，李宜强*，管错，陈诚

0 引言

目前，气驱提高采收率在国外发展速度快，效果佳，已成为其主要提高采收率技术之一，同时也是目前国内部分油田提高采收率的重要技术手段，利用气驱提高采收率的总量已经接近所有提高采收率产量的50%，在轻质油中比例更高[1]。常用的注气手段有连续注气(CGI)和水气交替注入(WAG)。水气交替注入(WAG)的出现就是为了解决在CGI中由于油气密度差异导致的重力超覆问题，尽管如此，WAG驱仍然无法完全克服重力超覆带来的弱波及问题。在解决重力超覆问题的过程中，WAG引起了与增加储层中含水饱和度有关的其它问题，包括降低了注气能力和加剧了水油流动的竞争[2]。为此，气体辅助重力泄油(GAGD)技术做为一种新兴注气手段开始受到人们的关注[3-5]。GAGD技术是利用已有的垂直井将气体注入到储层顶部，由于注入气与储层内原有流体之间的密度差会分离形成一个近水平的气-液界面，随着连续注入，气体向下运移并且体积横向扩大，然后界面被慢慢推向位于油水界面以上产层底部的水平采油井[6]。理论研究和矿场实践表明[7-10]，GAGD技术可以抑制黏性指进、扩大波及体积，提高微观驱油效率，极大地提升最终采收率。由于GAGD开发效果的影响因素较多，目前的研究主要通过量纲分析来研究GAGD相关问题。Geertsma等通过分析推导无因次群组，得到适合注气开发的无因次群组[11]，其中毛管数、邦德数和重力数应用最为广泛。一些研究已经应用无量纲组来研究黏性力、毛管力和重力对GAGD物理模型和理论分析模型的综合影响，以减少实验数量并获得预测石油采收率的模型。Grattoni等利用二维可视化模型各项参数易于控制的优点，对重力驱进行了系统研究。找到了毛管数、邦德数和重力数之间良好的相互关系[11]；针对单一无因次数预测效果差的问题，Kulkarni提出重力泄油数概念，将重力数、毛管数和邦德数组合成单一量纲数，给出了采收率与重力泄油数的对数关系式[12-13]；Wu等利用油气密度差和润湿性对重力泄油数进行了修正，给出了修正重力泄油数与采收率的对应关系[14]；Mohammad等考虑非均质性对采收率的影响，通过非线性回归方法给出采收率预测模型[15]。但上述模型针对GAGD非混相驱都存在预测准确性问题。本文基于量纲分析，利用室内实验、数值模拟和矿场数据，通过优化后的人工神经网络建立GAGD非混相驱采收率快速预测模型，并对比了遗传算法和粒子群算法两种优化方法的差异，给出最佳的优化模型。

1 GAGD开发油藏采收率影响因素

1.1 储层润湿性

储层岩石的润湿性质不仅决定了储层孔隙空间中的油气水分布，而且还影响着产油过程中的流体流动特性[16-17]。Grattoni等最早提出润湿性对注气辅助重力驱的采收率存在较大影响，研究表明，在油湿油藏中，油相已经作为连续膜存在于固体表面上，气体的注入可以有效地使油相膨胀，即使在较低的气体饱和度下也能够获得较大的采收率[11]；相反，对于水湿系统，油以分散状存在于孔隙中。注入气为了驱替残余油，首先要将残余油的物理形态从液滴转变为流动阻力较小的膜状，相同条件下，驱替出的油要明显少于油湿系统。Khorshidian通过微观可视化模型实验，更加详细的给出了润湿性对GAGD的影响[18]。油湿的采出程度比水湿要好，主要是因为油湿情况下，储层非均质性的存在，造成的小孔径的油相在油湿情况下毛管力是动力，孔径越小，越容易驱出；而水湿则相反。同时油湿还存在油的连续流动路径，可以带出更多的油。通过不同油气密度与黏度比的实验发现减小油气界面张力和油气密度差的比值可以提高水湿条件下非混相驱采收率，但是对于油湿系统的最终采收率的影响不大。Morrow等[19-22]通过室内实验和网格模型研究发现，混合润湿系统相较于水湿系统而言更有利于获得较高的采收率。

1.2 储层非均质性

层间和层内非均质性严重制约了采油过程的顺利进行，因为其控制着驱替中的流体注入的难易程度和波及类型。非均质性会为水平气体驱替带来一系列负面影响，如早期气体快速突破以及油藏波及效率低等问题[23-24]。相反，在重力稳定(垂直)气体驱替中，非均匀分层可以延迟由于气体分散作用引起的快速突破，并且还可以通过水平沉积的高渗透层抑制气体大量向下运移，从而改善最终波及效果[25]。Joshi等[26]提出在天然裂缝储层中使用水平井可以提高采收率，垂直井由于裂缝交叉导致有效排水的概率较高，采收率下降。天然裂缝储层通常具有非常低的基质渗透率，裂缝是其产量的主要来源。这一论点表明，与水平注气相比，油藏的非均质性对GAGD可能存在促进作用。Mahmoud等[27]用圆柱管近似代替天然裂缝设计了一套可视化模型来模拟天然裂缝油藏以研究裂缝对GAGD 的影响。结果证明将非混相GAGD 方法应用于裂缝性油藏中具有一定的可操作性，裂缝的存在对GAGD的采收率影响微乎其微。Watheq等[28]通过室内岩心驱替实验也验证了这一观点。因此对GAGD进行采收率预测时，只需考虑非均质性即可，不需要考虑油藏裂缝的发育情况。

1.3 可流动水饱和度

常规注气开发，可流动水的存在一定程度上阻碍了油气的直接接触，降低了混相的发生，同时也会导致开采初期出水严重的问题，极大地限制了注气效率从而降低了采收率。对于GAGD开发油藏，可动水饱和度的影响机制与常规注气相类似。Dumore 等在高渗透率岩心中进行了重力驱实验，发现岩心内部可流动水饱和度是重力驱替中获得理想采收率的关键因素。可流动水饱和度越高，GAGD效果越差，可流动水的存在降低了采收率[29]。Sharma等[30]利用烧结玻璃模型研究了可动水饱和度不同时，模型的采收率差异。结果发现，可动水饱和度不同的模型中，最终流体产量几乎不变，但高可动水饱和度模型的采油量远远低于低可动水模型。Delalat等[25]通过对伊朗西部某油田的数值模拟分析发现，储层中活跃水层的存在几乎可以使注气重力驱失去作用，而弱水层则对注气重力驱几乎没有影响。

1.4 铺展系数

铺展系数和润湿性影响气-油-水分布，从而影响气体注入油藏期间的采收率。铺展系数代表着油/水/气体系统中三个界面张力(IFT)之间平衡关系。式(1)为铺展系数的函数表达式：

式中：σt为流体铺展系数，N/m；σgw为气水界面张力，N/m；σgo为气油界面张力，N/m；σow为油水界面张力，N/m。

铺展系数数值对于确定三个共存于储层内的相之间的平衡扩散特征是至关重要的。流体扩散特性严重制约着气驱原油采收率，特别是在气体辅助重力驱替中。Rao[31]概念性地总结了各相在储层内的空间分布对铺展系数和润湿性的依赖性。从石油开采的角度，提出正铺展系数条件对于提高采收率是有利的。Oren等利用微观模型实验[32]可视化地表征了润湿性和流体间扩散对气体驱替采收率的影响，证明铺展系数的正值有助于确保注入气体和储层之间连续油膜的形成，从而使注入气体与储层内水相的接触机会大大减少，减弱了油水的竞争流动。铺展系数为负值表示在水和气体之间存在不连续的油分布，原油很难形成连续油膜，气水接触，从而降低了原油采收率。

1.5 流体物理性质

对于连续注气(CGI)和水气交替(WAG)而言，在油藏内部，由于油气密度差使得注入气上浮形成超覆作用，导致波及系数大大降低，严重影响油气采收率。然而对于注气辅助重力驱而言，这种重力分异作用却对采收率起着增益作用，使得波及系数明显增大，很大程度上抑制了黏度指进且延缓了气体过早的突破。油气黏度和油气黏度比主要是影响油气界面的稳定性。可通过调整油气流度比，延缓气体突破[30]。

1.6 注气速度

油气界面的稳定对GAGD开发效果的影响巨大，在各类影响因素中，注气速度被公认为是影响界面稳定性的主控因素。注气速度过大，容易造成指进和舌进现象，导致气体突破时间大大提前，波及效果差，采收率低；相反，如果注气速度过低，虽然可以保证油气界面在驱替过程中稳定运移，但是驱替时间大大增加，生产成本高，经济性较差。Mahmoud等[27]开展了不同注入速率的注气辅助重力驱实验，在保证稳定油气前缘的基础上发现注入速率越高，可视化模型内的GAGD最终采收率越高。Meszaros[33]采用相似准则设计不同维数物理模型研究注气辅助重力驱。结果表明，低压时用注气稳定重力驱技术采收率可达70%以上，远高于非稳定重力驱。为了获得最佳的开发效果，理想的情况是找到获得稳定驱替前沿的最大注气速度，有学者将其称为临界速度。国外众多学者对临界速度进行了研究，并得到了不同的临界速度公式(表1)。其中Dumore标准广泛应用。

表1 各类临界速度Table 1 Different kinds of critical speeds

2 量纲群组分析

通过文献调研不难发现影响GAGD开发效果的因素众多，在建立采收率预测模型的过程中，为了得到较为精确的预测模型，要充分考虑各因素的影响。对于室内物理实验和实际油田的开发，这些参数往往存在很大差异，极大的削弱了预测模型的泛化能力。量纲分析被认为是一种有效的分析手段，可用于减少充分描述这些变量之间关系所需的实验变量的数量。在许多科学和工程应用中，特别是实验工作中，系统变量之间的数学关系是未知的[38]。大部分过程变量的实验评估和验证不可行或有时甚至不可能，量纲分析都可以很好的解决这些问题。

对于注气辅助重力驱，目前常用的无因次群组见表2，基本囊括了影响GAGD开发油藏采收率的各项参数，如储层非均质性、润湿性、铺展系数、流体性质等。其中毛管数、邦德数和重力数被认为是描述GAGD过程的最佳参数。值得说明的一点是Dykstra Parson系数是Mohammad提出的用来表征储层非均质性的参数[15]。早期研究仅将储层非均质性视为垂直与水平渗透率比值，在注气辅助重力泄油(GAGD)中，渗透率非均质性定义为储层中不同的渗透率分布，由这些渗透率分布函数产生另一个无量纲数，即Dykstra-Parson系数。大量研究表明，注气辅助重力驱最终采收率随着毛管数的增加而增加，但是，对于某一特定油藏，在非混相驱替时很难明显降低油气界面张力，故注入速度是决定毛管力大小的主要因素，但是受限于注入工艺，注入速度并不能无限增大，而且当注入速度过大时，会破坏油气稳定前缘，反而不利于采收率的增加。邦德数是重力与毛管力相对关系的表现，重力数是邦德数和毛管数的比值。研究表明邦德数和重力数越大，采收率越高，说明重力驱动是主要的生产机制。不过Bautisya的最新研究表明[40]，对于注气辅助重力非混相驱，在气体突破前，较低的毛管数和邦德数，较高的重力数更有利于采收率的提高；相反，在气体突破后，较高的毛管数和邦德数，较低的重力数更有利于采收率的提高。可见注气辅助重力非混相驱的采收率与毛管数、邦德数以及重力数之间存在某种关联。

表2 GAGD量纲数群组Table 2 Dimensional group of GAGD

为了研究采收率与量纲组之间的最佳相互关系，目前已有学者给出了利用量纲群组预测注气辅助非混相驱采收率的方法，见表3。Rostami等[41]考虑毛管数、邦德数和黏度比，给出预测公式。尽管该公式的预测精确度大大增加(R2=0.9104)，但是所考虑到的无因次量纲数量较少；Kulkarni等[13]考虑油气密度差对采收率的影响，将毛管数、邦德数和重力数结合起来定义为重力泄油数，并给出了非混相驱采收率与重力泄油数关系；WU[14]考虑了接触角和油气黏度比，对重力泄油数进行修正并重新给出预测公式，但该公式并没有考虑油藏的非均质性；Mohammad[15]充分考虑了油藏参数如油层尺寸、油藏非均质性等对采收率的影响，利用油藏数值模拟和非线性拟合等手段给出了相关预测，虽然该方法得到的结果与室内物理模拟结果具有一致性，但仍然存在预测精度不高且对实际油田采收率预测结果较差的问题。

表3 GAGD非混相驱采收率预测模型Table 3 GAGD immiscible displacement recovery prediction model

国外Lepski和Bassiouni提出储层倾角大于10°的油藏更有利于顶部注气重力驱[42]；杨超认为油藏倾角越大越有利于顶部注气重力驱[43]，他根据国内实施顶部注气油藏的特点，将顶部注气重力驱可发挥作用的临界储层倾角定为13°，可见，储层倾角大小对GAGD的开发效果影响显著。在GAGD中，重力通常作为驱替动力，毛管力通常作为驱替阻力，储层倾角大小的意义就在于倾角越大，重力发挥的作用就越明显，克服毛管力的能力就越强，越有利于GAGD提高采收率。针对此特点，本文对包含重力作用与毛管力作用的无因次参数——邦德数进行修正。考虑到实际油藏在进行GAGD时，为了得到最佳的采收效果，通常会控制注入速度来保证油气界面的稳定，故这里采用迪茨模式下的重力稳定驱方式并利用油藏倾角对邦德数的重力项进行修正。图1为迪茨模式的几何关系图。

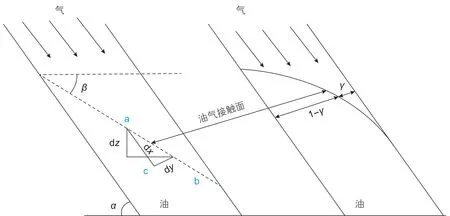
图1 迪茨模式的几何关系Fig. 1 Diez geometrical model

用达西定律以势能的形式表示出沿x轴的情况

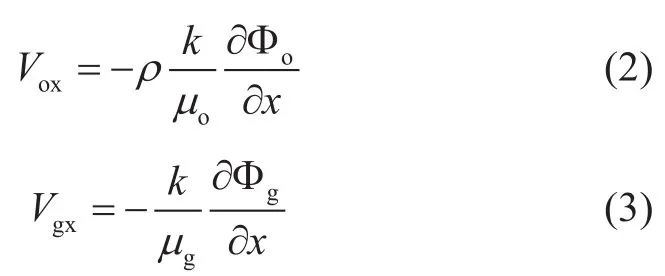
单元流体的势能定义为：

z值向上为正，因流体被看成不可压缩，故(4)式积分可得

假设界面相对地层垂向厚度而言很长，这样Φb近似等于Φc，则沿着界面ab的油相和气相的势能差为：

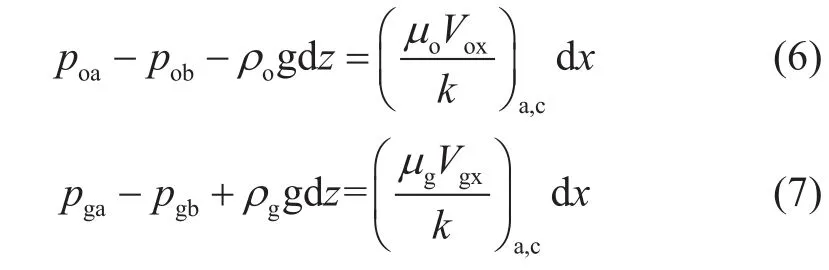
假定界面上的毛细压力不变，方程变为

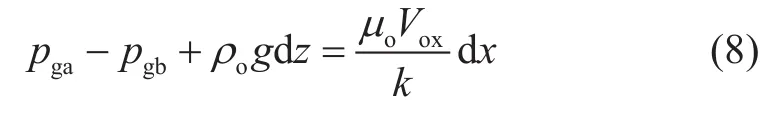
式(7)减去式(8)得：

由图1中几何关系可知

如果界面是稳定的，沿着与地层平行的流线始终有Vox=Vgx=V的关系，由此式(9)可以写成

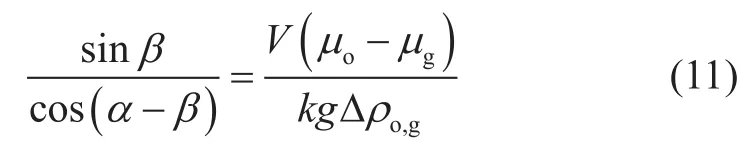
考虑到实际油藏稳定界面几乎都为倾斜界面，故式(11)可以解为

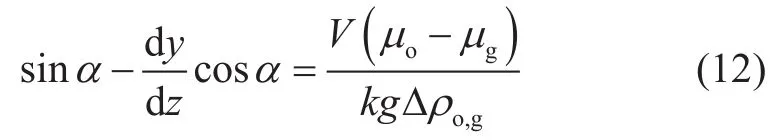
上式右端为黏滞力项，左端即为考虑油藏倾角时的重力项，将其作为邦德数中的重力项，则修正后的邦德数为

式中：Nb′为修正邦德数；α为油藏倾角；Δρ为油气密度差，g/cm3；σ为油水界面张力，N/m；k为绝对渗透率，um2；µ为重力加速度，m/s2；µ为黏度，mPa·s。为了提高预测精度，我们引入了机器学习算法来对数值模拟数据、室内物理模拟实验数据以及部分油田实际生产数据进行分析[14-15]，并利用不同优化算法对分析过程进行优化，以期得到更为精确的预测模型。在本文中，采收率预测模型ζ的一般表达式为：

3 优化人工神经网络预测模型

BP神经网络(BNN)是一类多层的前馈神经网络。在网络训练的过程中，以设定的误差精度为界限，不断的调整权值，直至达到预设精度。这种反向传播的学习算法，即为BP学习算法。BP神经网络一般而言具有一个或数个sigmoid隐藏层和输出层，可以对非连续函数拟合逼近。在本文中，建立三层网络结构模型，在三层网络中，输入层进行参数输入，通过上节的量纲分析，我们确定了6个输入量纲参数，因此输入层神经元个数为6。隐含层神经元个数选择分别13、30和50，通过结果对比选择预测效果最佳的隐含神经元个数。输出层代表最终预测参数，故输出层神经元个数为1，代表采收率。初始权值和阈值的选择对最终网络模型的精度影响较大，其取值通常为随机赋值，这会对模型的预测准确性产生负面影响，为了克服这一缺陷，笔者采用优化算法对BP神经网络进行优化，本文选取粒子群算法和遗传算法来实现对BP神经网络的优化。

3.1 遗传算法优化BP神经网络

遗传算法(GA)是J.Holland等人于1975年仿照生物界优胜劣汰，适者生存的机制演化而来的一种优化算法。其主要特点是适用性强，既可以对非连续函数进行操作，又可以直接面向无函数关系的对象进行直接操作，自适应能力与全局寻优能力尤为突出。鉴于生物进化论理论，遗传算法能够自主利用概率方法进行自优化，获得最佳优化域，整个过程完全由算法自主选择，不需要人为的设置限制条件。遗传算法优化BP神经网络是用遗传算法来优化BP神经网络的初始权值和阈值，使优化后的BP神经网络对样本的预测精度更高。本文遗传算法参数如下：个体数目和遗传代数均设为40；代沟为0.95；交叉概率0.7；变异概率0.01。

3.2 粒子群算法优化BP神经网络

粒子群优化算法(PSO)是一种进化计算技术，1995 年由Eberhart 博士和kennedy 博士提出，源于对鸟群捕食的行为研究。粒子群优化算法的特点是通过个体之间通力协作，共享信息来获得最优域。PSO的优点是比遗产算法更容易实现并且需要人为设置的参数较少。粒子群算法优化BP神经网络是用粒子群算法来优化BP神经网络的初始权值和阈值，使优化后的BP神经网络能够更好地进行样本预测。本文粒子群算法参数如下：粒子群规模为50；粒子维数分别选择13、30和50；惯性权重取定常值为1，学习因子为1.494 45；粒子速度介于1与-1之间，粒子位置范围介于1与-1之间。

4 结果与讨论

预测模型所用数据见表4和表5。首先，本文先对文献中报道的考虑量纲数最为全面的非线性模型进行测试[15]。该方法使用非线性回归方法提供了一个新的组合数，其中包括所有无量纲数。该组合数如下：

表4 物理模拟与实际油田的量纲计算值[13,31]Table 4 Dimension calculation of physical simulation and actual oil field[13,31]

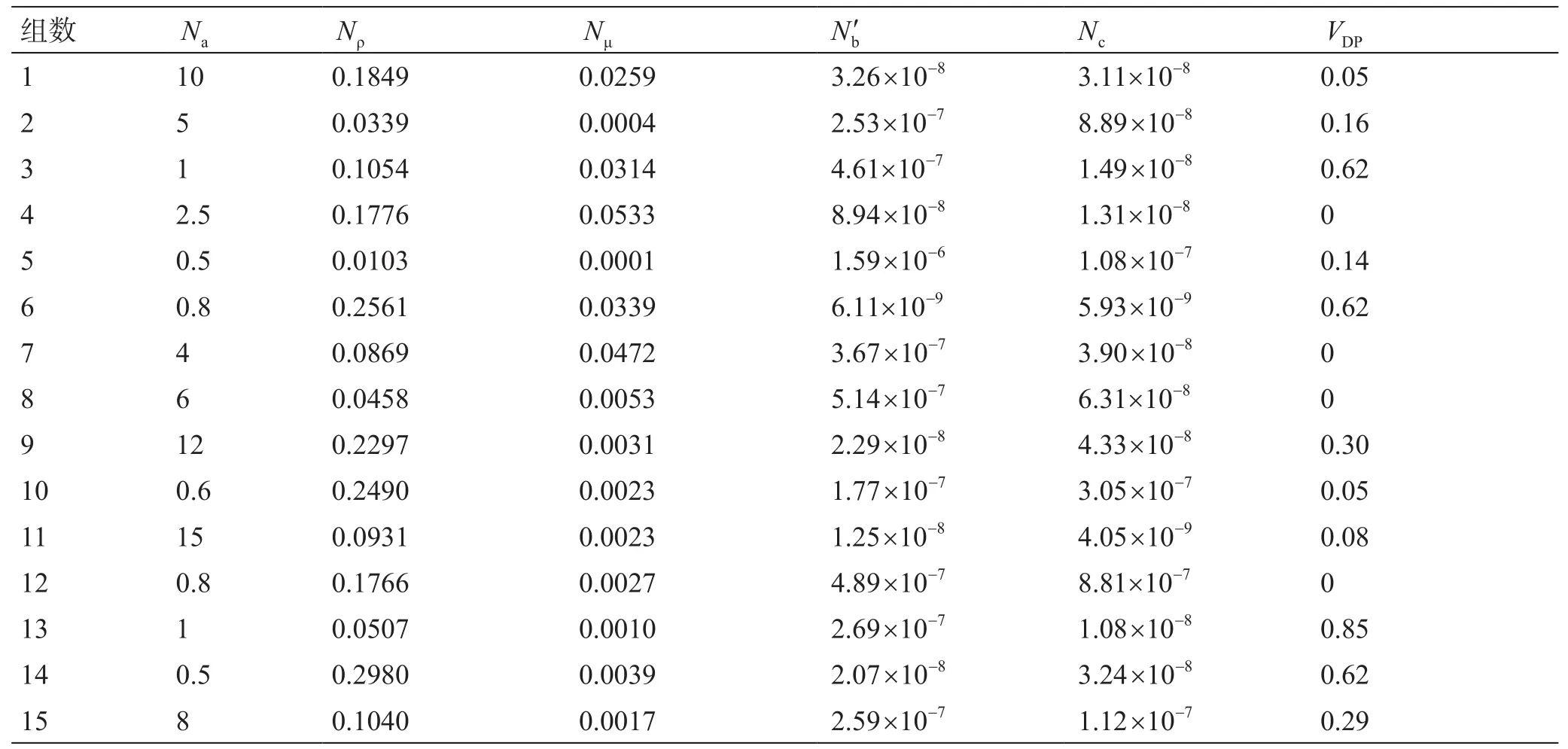
表5 数值模拟实验量纲计算值[15]Table 5 Dimension calculation of numerical simulation[15]

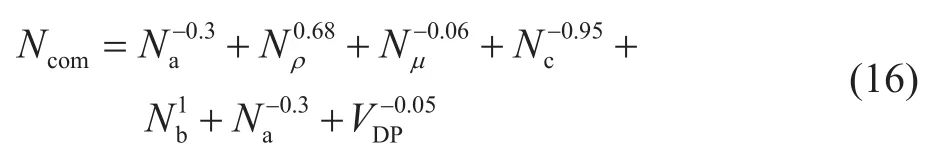
利用该组合数，Mohammad等[15]人建立了采收率预测公式：

将物理模拟和实际油田数据利用该公式进行预测计算，结果见图2。

由图2不难看出，非线性模型对于数值模拟的预测结果令人满意，预测结果多位于预测-实际理想关系曲线附近；对于物理模拟结果与实际油田数据的预测误差较大。说明仅仅依靠量纲参数之间简单的组合运算，很难准确地预测出GAGD非混相驱开发油藏的采收率。

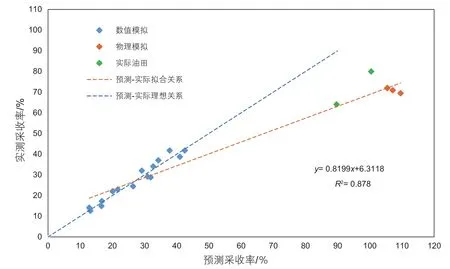
图2 非线性模型预测结果Fig. 2 Nonlinear model prediction results

4.1 优化神经网络模型预测结果

建立模型过程中，我们选择数值模拟1～11组以及物理模拟1、2组为训练样本，其余数据作为测试样本，目的是利用训练样本得到的模型对测试样本进行预测，从而检验模型是否具有泛化能力。具体结果见图3和图4。

图3 隐藏节点数为50时GA-BP预测结果Fig. 3 GA-BP prediction result when the number of hidden nodes is 50

图4 隐藏节点数为30时PSO-BP预测结果Fig. 4 PSO-BP prediction result when the number of hidden nodes is 30

不同模型预测结果见表6，利用机器学习算法进行预测，得到的结果相比于非线性拟合方法，相关性都有所提高。当遗传算法网络模型结构隐藏层节点数为13和30时，模型对于物理模拟和数值模拟结果的预测效果较好，对于实际油田结果的预测误差非常明显；当节点数增至50时,实际油田预测效果明显提升，预测值与实际值的拟合相关系数可以达到0.9635。理论上无限增加节点数可以使预测精精度无限提升，但是相对应的预测模型计算时间会呈现几何倍数增长，大大削弱了预测模型的快捷性。对于粒子群算法，预测效果随着节点数增加并没有明显提升，但是该预测

模型计算时间远少于遗传算法模型。由以上结果分析可知隐藏节点数为50的GA-BP预测模型和隐藏节点数为30的PSO-BP预测模型预测精度更高。

表6 不同模型预测结果Table 6 Different model prediction results

4.2 不同模型预测误差分析

将3种模型预测得到的各组结果进行误差计算，结果见图5。从预测误差效果来看，3种预测模型对于数值模拟数据的预测误差比较接近，非线性模型对于物理模拟数据和实际油田数据的预测误差要明显高于机器学习方法。对比两种机器学习方法，发现遗传算法优化后的神经网络预测模型的预测精度要远高于粒子群算法优化神经网络模型。可见，利用遗传算法优化后的BP神经网络模型更适合用来对注气辅助重力非混相驱的采收率进行预测，分析结果表明该类模型可以很好地作为GAGD油藏采收率评估的替代手段。

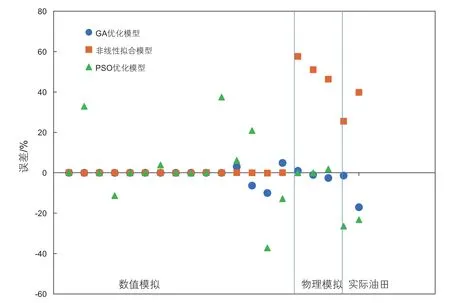
图5 不同模型采收率计算误差对比Fig. 5 Comparison of calculation error of different model recovery factors

5 结论

提出了一种用于预测GAGD非混相开发油藏采收率的神经网络模型。该模型以影响GAGD开发效果参数构成的无量纲数为输入项，模型建立过程中对其中的无量纲邦德数利用油藏倾角进行了修正。同时为了保证模型的预测准确率，分别利用遗传算法和粒子群算法对神经网络模型参数进行优化。结果表明，基于量纲分析的神经网络预测模型可用于估算任何给定非混相油藏的采油潜力。优化后的神经网络预测模型可以很好地作为GAGD非混相油藏采收率评估的替代手段。值得注意的是，本文所提出的预测模型仅适用于GAGD非混相油藏。对于GAGD混相油藏采收率的预测，本模型存在很大的局限性，原因在于模型中的关键参数毛管数和邦德数在混相条件下可以认为是不存在的。