多模式集成分级降水概率及落区预报试验*

吴振玲，张 楠，徐 姝，董 昊，汪 靖

(1.天津市气象台，天津 300074；2. 天津市气象局，天津 300074)

降水是天气要素预报业务中难度最大，挑战性最强的天气要素，当其降水强度较大时，常给人民生命财产及工农业生产带来严重危害[1-4]。且近年来，随着数值预报技术的发展，降水预报的准确率得到了一定程度的提高[5]，但是天气预报存在着不可避免的不确定性[6-7]，任何数值模式都无法准确无误地描述真实的大气过程，所以单一模式确定性预报水平的提高已经变得越来越困难[8-9]，并且实际业务中预报员要面对很多的预报产品，对预报产品的使用依赖于预报员的主观判断，因而带来较多的主观性。

为消除降水预报的系统性误差，统计方法在降水预报产品释用方面得到了较为广泛的应用，如Leslie[10]采用统计回归方法，使用模式预报结果和3个统计预报因子对澳大利亚东南部天气系统进行集成组合预报，Hamill等[11-12]也提出使用Logistic回归方程对降水数值预报进行订正，这些都使得预报质量得到显著提高。但是，预报员每日面对的模式数值预报产品种类繁多，导致预报员很难在短时间内有效地利用这些预报信息，这也促使了多模式集成预报方法在国内气象部门的快速发展[13]。在多模式集成研究方面，金龙等[14]，魏凤英[15]，陈桂英等[16]分别采用神经网络方法，区域动态权重方法，分区权重法，研究了降水集成预报，预报的准确率高于单一集成成员的预报结果，但这些方法无法将预报的不确定性描述出来。

概率预报是表达预报不确定性的一种方式，而多模式集成预报则是获得概率预报的一种有效途径。目前预报业务中最常用的办法是“平均法”，即给予每个模式成员相同的权重，根据预报发生某天气现象的成员个数来确定未来该天气现象发生的概率[17-19]，Hamill和Colucci[20-21]提出一种概率预报新方法(Rank方法)，即根据前期各模式成员的等级分布以及各成员的预报结果确定未来某天气现象发生的概率，根据王晨稀[22]和陈超辉[23]的预报试验表明，Rank方法的概率预报效果要好于平均法，但王晨稀[22]的预报试验是利用有明显降水过程的个例统计的等级分布，并且试验对象也是明显的降水过程，陈超辉[23]的试验对象主要为7月盛汛期的降水过程。但如果需要将降水概率预报业务化，无论降水过程是否明显，有雨无雨都要输出概率预报产品，这就要求统计的对象不仅仅局限于明显降水过程，因此，针对业务需求，需要进一步设计基于Rank方法的概率统计方案。

本文将EC-thin，JAP，GER，T639、TJ-WRF模式作为集成降水概率预报模式成员，设计了基于Rank方法的概率预报方案，对天津地区2014年4-10月232个自动站点进行降水概率预报试验，对比其与业务上常用的平均法和相关法[22]的预报效果，并讨论了多模式集成概率预报产品在降水落区预报中的应用方法。

1 资料与方法

1.1 资料来源

数值预报资料来源于2013年、2014年4-10月每日20时欧洲中心模式(EC-thin)，日本模式(JAP)，德国模式(GER)，T639模式(T639)以及天津本地WRF模式(TJ-WRF)5个集成模式成员的格点降水预报，结合预报业务应用时段，每日选取2段12h累计降水预报。实况资料选取与模式相同时段的天津232个区域自动气象站的降水量资料。

2013年资料用于建立集成降水概率预报统计模型，2014年资料用于集成降水概率预报试验。

1.2 资料处理

将EC-thin，JAP，GER，T639、TJ-WRF模式作为集成降水概率预报模式成员的格点预报数据利用双线性插值方法转换为天津232个自动雨量站的站点预报数据。

1.3 集成降水概率及落区预报方法简介

1.3.1 Rank方法

(1)建模样本筛选

利用2013年4-10月的降水资料，共筛选出39797个建模样本，每个样本需要满足如下两个条件：①五个模式逐12 h降水预报资料完整；②任一自动站点的数值预报有一个以上的成员预报该站降水或该站点实况出现降水，即可作为一个统计样本。

(2)降水等级分布概率统计

将5个集成模式成员按预报降水量(R)从小到大进行排列R1、R2、R3、R4、R5，当实况降水V≤R1，排列为等级1；当实况降水R1R5，排列为等级6，形成6个等级，其对应的实况可能位于6个等级中的任一等级。积累一定量的样本, 判断每个样本降水实况对应的等级, 进而统计降水实况位于每个等级的概率即等级分布。为满足集成降水概率预报的业务需求，本文没有直接对所有样本进行统计，而是根据预报有降水的模式数量将样本进行分类，然后再按照Rank方法分类统计其等级分布，如表2按预报降水的模式个数分类统计各等级的概率分布所示，当1个模式预报降水时，R1=R2=R3=R4<0.1，R5≥0.1，统计实况位于等级5、等级6的概率(等级分布)，当2个模式预报降水时，R1=R2=R3< 0.1，R4≥0.1、R5≥0.1，统计实况位于等级4、等级5、等级6的概率，以此类推，当5个模式全部预报降水时，统计实况位于等级1、等级2、……、等级6的概率。

表1 按预报降水的模式个数分类统计各等级的概率分布

(3)降水分级概率预报规则

根据该方案统计得出的实况位于各个等级的概率分布，以及2014年4-10月各集成模式成员的预报结果，即可对2014年汛期降水概率进行预报试验。具体方法与王晨稀等[22]利用的方法一致。

(4)降水落区预报方法

采用概率阈值的方法将集成概率预报转化为集成确定性预报。根据计算的多模式集成的分级降水概率，设定不同的分级降水预报概率阈值，对达到或超过阈值的降水预报的击中率POD、误报率FAR、预报偏差bias及综合评分ETS进行评分，选取最佳集成概率阈值，将集成分级降水概率预报转换为确定性降水及落区预报。

2 集成降水概率预报试验分析

从2014年4月1日20时起，利用Rank方法、平均法以及相关法对天津232个自动站点进行逐12 h分级降水概率预报。预报分为两个时效区间： 08时至20时为第一时效区间，20时至08时为第二时效区间。

2.1 试验样本

2014年4-10月期间，除37d数值模式缺少数据外，共计176 d有效资料，那么每个时效区间共有176个试验时段，共计352个试验时段，由于天津共有232个自动站点，则每个时段内共有232个试验样本，共计试验样本数232×352=85 376个。

2.2 RPS评分

RPS评分是对多个等级的概率预报结果给出综合评价的一个指标，其值越小越好，为0时效果最好。表2为三种方法降水概率预报的RPS评分，在第一时效区间和第二时效区间的预报试验中，Rank方法得到的概率预报的RPS评分平均值最低，平均法次之，相关法最高，表明Rank方法的集成概率预报误差最小，比平均法和相关法的降水概率具有更好的预报准确性。

表2 三种方法降水概率预报的RPS评分

图1 三种方法在各个试验时段的RPS评分结果

图2 三种方法各级降水概率预报的BS评分

对两个时效区间内每个试验样本的集成概率预报进行RPS评分(图1)发现，352个试验预报中，83.5%基于Rank法的预报的RPS评分小于平均法和相关法，也说明Rank方法的集成降水概率预报准确率高于平均法和相关法。

2.3 BS评分

BS评分值RBS是对某一等级降水的概率预报结果进行评价的一个指标，其值也是越小越好，为0时说明效果最佳。图2为三种方法各级降水概率预报的BS评分，对比了三种概率预报方法对各个量级降水的预报准确率。降水量级越大，BS评分相对越小，这与统计方法有关，并不能说明三种集成概率预报方法对量级大的降水的概率预报效果好于对量级小的降水的概率预报效果[22]，因此，在此仅分析不同方法相同量级降水的概率预报效果。对于各级降水概率集成预报，平均法和相关法的评分基本相当，相关法预报误差最大，Rank方法评分总体上都比平均法和相关法小，BS评分小于0.1，概率预报误差小于平均法和相关法，尤其是无雨和小雨概率预报准确率高。在无雨概率预报中，在第一时效区间，Rank方法的BS评分小于平均法的幅度为20%，在第二时效区间小于平均法的幅度10%；在小雨概率预报中，第一时效区间Rank方法的BS评分小于平均法的幅度为23%，第二时效区间预报小于平均法的幅度为13%；对于中雨和大雨的预报，虽然三种方法的BS评分差异不大，Rank方法的优势不特别明显，但是Rank方法预报误差仍是最小的，低于其他两种方法，对于暴雨预报，三种方法的BS评分都较小，基本持平。

图3 Rank方法(红色实线)、平均法(绿色实线)以及相关法(黑色实线)对应的ROC曲线

表3 不同阈值降水预报准确率和ETS评分

2.4 ROC曲线

ROC曲线反映的是某量级降水概率预报结果命中率和假预警率的关系，当ROC曲线位于对角线上方时为有技巧预报，此时ROC曲线下方的面积(称为ROC面积)>0.5;当ROC曲线位于对角线下方时为无技巧预报，此时ROC面积<0.5；图3为利用Rank方法、平均法以及相关法的各量级降水的概率预报产品绘制的ROC曲线。无论小雨、中雨、大雨还是暴雨，三种方法的ROC曲线均位于对角线上方，即ROC面积大于0.5，但随着降水量级的增大，ROC曲线的面积在减小，表明利用这三种方法对各个量级的概率预报都是有技巧预报，且对量级小的降水概率的预报技巧要高于高量级降水，这与王晨稀[22]得到的结论是一致的。在各个量级的降水中，平均法和相关法的ROC曲线几乎是重合的，表明这两种方法对各个量级降水的概率预报效果是基本一致的， Rank方法在各个量级降水的ROC曲线下方的面积均大于另外两种方法，说明Rank方法的预报效果要好于平均法和相关法，在小雨预报中，虽然Rank方法的ROC曲线下方的面积大于平均法和相关法，但非常接近，表明Rank方法的预报效果优势并不明显。而在中雨、大雨、暴雨预报中，Rank方法的ROC曲线明显在平均法和相关法上方，表明在这三个量级降水的概率预报中，Rank方法的优势明显，这一结论与上文中BS评分结果不一致。这主要与评价方法的侧重点不同有关，前者统计的是降水概率预报的均方差，后者统计的是命中率和假预警率的相对关系。

3 降水落区预报应用试验

通过三种多模式集成降水概率预报方法的试验分析，发现Rank方法的概率预报准确性要高于平均法和相关法，因此，这里探讨了基于Rank方法集成降水落区预报，将集成概率预报转化为集成确定性预报。

3.1 晴雨预报概率阈值选取

选取2014年4月1日-10月30日所有样本的降水概率预报结果，分别统计当这一阈值等于10%，20%，30%，40%，50%，60%时，降水正确、降水空报、降水漏报以及晴预报正确次数。表3给出了当选择不同阈值时降水正确、空报、漏报、晴正确次数以及晴雨预报准确率和ETS评分，晴雨预报准确率和ETS评分计算公式如下：

(1)

(2)

(3)

式中：NA代表预报降水，实况也出现降水；NB代表预报降水，而实况没有出现降水；NC代表没有预报降水，而实况出现降水；ND代表没有预报降水，实况也没有出现降水。

由表3可知，当阈值取10%时，降水预报正确次数最多，但空报也最多，因此晴雨预报的准确率和ETS评分都是最低的，随着阈值的加大，空报次数减少，预报效果有所改善，当阈值取40%时，晴雨预报准确率可以达到0.85，降水ETS评分也能达0.343 7，效果最好，当阈值取50%以上时，虽然晴雨预报准确率略有上升，但降水漏报次数明显增多，导致ETS评分效果不佳。因此取40%为最佳概率阈值。

3.2 分级降水预报概率阈值选取

根据晴雨预报的概率阈值选取方法，确定各个量级降水预报的概率阈值。经过多次试验选取，小雨预报的最佳概率阈值为17%时，ETS评分最高，为0.248 7；中雨预报的最佳概率阈值为17%时，ETS评分最高，为0.157；大雨预报的最佳概率阈值为8%时，ETS评分最高，为0.093 6；暴雨预报的最佳概率阈值为1%时，ETS评分最高，为0.020 2。由此可以看出，对于中雨以上量级的降水，降水量级越大，其对应的概率阈值越小，这可能是由于大部分模式成员的空间分辨率较低，对局地性的较大量级降水的预报能力较弱，导致对较大量级降水预报的概率较低，如对暴雨的概率预报，所有样本中预报的最大概率也仅为18%。

表4 各量级降水概率预报最佳概率阈值选取及ETS评分

图4为基于多模式集成概率阈值给出的降水预报产品的ETS评分与各个模式成员各量级降水产品的ETS评分对比，在不分量级的降水预报中，基于概率阈值的降水产品的ETS评分为0.34，较单一模式中最高的EC模式的ETS评分高出6%，在小雨量级预报中，基于概率阈值的降水产品的ETS评分为0.25，较单一模式中最高的T639模式的ETS评分高出100%，对于中等以上量级的降水，单一模式的ETS评分均在0附近，而基于概率阈值的降水产品的ETS评分均为明显的正值。由此表明，基于多模式集成概率阈值给出的降水预报产品的ETS评分都要明显高于单一模式成员降水预报的ETS评分，且在分级降水预报中，多模式集成产品优势更加明显。

图4 基于概率阈值给出的降水预报产品与单一模式降水预报的ETS评分

3.3 概率预报落区检验

将2014年4-10月352个试验时段进行逐时段的多模式集成降水概率预报与实况降水落区对比。

3.3.1 预报降水落区定义

根据本文确定的最佳集成概率阈值，将集成降水概率预报大于等于40%的站点判定为预报降水站点，小于40%的站点判定为预报无雨站点，将所有预报降水站点围成的区域定义为预报降水落区。352个时段中有133个时段有预报降水落区。

3.3.2 降水落区击中判定原则

如果某试验时段降水预报正确站数大于空报站数和漏报站数，或者实际发生降水的全部站点为预报正确站点，定义此试验时段为降水落区击中，如果某时段降水未定义为降水落区击中，则需判断是否为降水空报或漏报时段：如某时段空报站数大于正确站数和漏报站数，则定义此时段为降水空报时段，如某时段漏报站数大于正确站数和空报站数，则定义此时段为降水漏报时段。

3.3.3 落区预报检验分析

通过对352个预报时段进行检验分析，落区预报击中72例，少部分击中4例，空报22例，漏报90例。通过逐个时段分析，发现漏报的90例中有66例都是局地性降水，而且降水站数不足20站，相对天津232个站点，所占比例仅为8.6%，降水区域非常小(图5)，对天津降水落区统计没有实际意义，因此，滤去66例局地性降水个例。落区预报击中准确率达到62.3%。在图5中分别列举了3个试验时段多模式集成降水概率预报与实况降水的对比图。对比图5中各图发现2014年5月1日白天为降水落区击中时段，多模式集成预报大于40%的区域和实况降水发生的位置都是在天津北部；9月1日夜间为降水落区全区击中时段，多模式集成预报大于40%的区域覆盖天津全区，而实况也是全区发生降水；图5也展示了漏报时段，4月9日夜间，天津地区没有出现多模式集成预报大于40%的区域，但实况在东部局部地区出现了小雨，降水发生站数较少，对天津降水落区统计没有实际意义。

3.3.4 典型个例落区检验

选取2016年7月20日全区暴雨以及2017年8月27日全运会开幕式降水过程预报为例，分析基于Rank方法的降水预报落区对区域极端灾害性天气过程以及一般性降水过程的预报能力。

(1)暴雨落区预报分析

图6为 7月20日暴雨落区预报与实况对比，提前24 h多模式集成分级降水概率预报结果显示，2016年7月20日白天(08时-20时)全区降水概率均达到或超过暴雨概率阈值标准，图6中暴雨概率预报落区表明，天津将出现全区性暴雨。同期降水实况显示，20日白天天津95.3%的自动气象站点的降水量超过暴雨标准50 mm，85.6%站点出现大暴雨或特大暴雨，其他几乎为大到暴雨，只有一个站点为中到大雨，与实况非常吻合。对比分析表明基于Rank方法的集成概率预报和基于概率阈值的降水落区预报，对小概率极端性的暴雨落区预报具有很好的预报性。

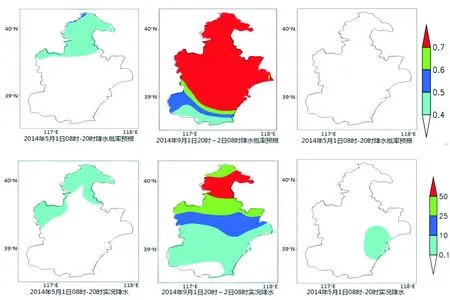
图5 Rank方法降水概率预报(阴影，大于等于0.4的部分)和实况降水量(阴影，单位：mm)对比

图6 2016年7月20日08:00-20:00暴雨落区预报(阴影)和实况降水量(阴影，单位：mm)对比

(2)一般性降水落区分析

图7为8月27日一般性降水落区预报与实况对比，2017年8月27日白天(08:00-20:00)的全区降水概率预报均超出0.4的降水判断阈值标准，其中天津南部降水概率达到中雨判断阈值标准，表明天津将出现全区性降水过程，中南部等部分地区将有中雨。同期降水实况显示，27日白天天津普降小雨，中南部的市区、西青、东丽、津南、静海、滨海新区等地达到中雨量级，提前24 h落区预报分布与实况基本吻合。27日夜晚(27日20:00-28日08:00)集成分级降水概率落区预报显示，全区性降水继续维持，中雨落区预报北移。同期降水实况显示，天津普降小雨，其北部的蓟州、武清、北辰、宁河等出现中雨降水。对比分析表明，根据Rank多模式降水概率预报和前文确定的分级降水概率阈值，对概率较大的一般性降水落区预报也有很好的预报效果。虽然27日夜间中雨落区预报面积较小，但是对降水强度落区移动方向有很好的指示意义

4 结论

本文利用EC-thin，JAP，GER，T639以及TJ-WRF五种业务常用数值模式的格点降水预报资料和历史实况资料，分别基于Rank方法、平均法、相关法设计了三种集成降水概率预报方案，并对2014年4-10月进行集成降水概率预报试验及RPS、BS评分、ROC曲线检验，探讨了集成降水概率预报产品在降水落区预报业务中的应用方案。

(1)通过对2014年4-10月进行多模式集成降水概率预报试验发现，无论是预报概率的BS/RPS检验，还是ROC曲线检验，Rank方法得到的降水概率预报比平均法和相关法具有更高的预报准确性，所不同的是对于BS检验，Rank方法对于小雨的概率预报均方差要明显小于其他两种方案，但对于中雨-暴雨的预报，Rank方法的优势不明显，而对于ROC曲线检验，Rank方法对于中雨-暴雨的概率预报效果要明显优于其他两种方案，但对小雨的优势不明显；

(2)基于Rank方法的多模式集成降水概率预报对降水具有较强的可预报性，通过降水概率阈值的试验分析，发现当集成降水概率预报达到40%时，降水预报准确率高，晴雨预报准确率可达到85.1%，TS评分也将达到0.43，基于多模式集成概率阈值给出的降水预报产品的ETS评分都要明显高于各个模式成员降水预报的ETS评分，且在分级降水预报中，多模式集成产品优势更加明显；

图7 降水落区预报产品(阴影)、中雨落区预报产品(阴影)实况降水量(阴影，单位：mm)的对比

(3)分级降水落区预报检验表明，通过分析选取的集成分级降水概率判断阈值进行的分级降水落区预报，对大范围降水有较好的指示意义和可预报性，降水落区预报击中的准确率达到62.3%。典型个例分析显示，对天津小概率极端性的全区性暴雨落区和概率较大的一般性降水落区均有较好的预报效果。

5 讨论

基于Rank方法的多模式集成降水概率预报对降水具有较强的可预报性，集成降水概率预报大于40%的区域对降水落区具有一定的指示意义，但对局地性降水的漏报较多，其主要原因为以下2个方面：一方面模式对小尺度局地对流降水过程预报本身存在时间和空间误差；另一方面数值模式资料的空间分辨率较低，而天津的自动气象站点较密，由低分辨率向高分辨率转换过程中，可能放大数值模式预报的误差，增强了局地性对流降水预报的难度。