基于多级模糊数学的矿山地质灾害指标体系设计*

王 继

(四川财经职业学院，四川 成都 610101)

金属矿山地质灾害是当前地质灾害研究的又一个分支，并且是最可能直接诱发地质灾害的一种。其是在人为或自然因素的作用下产生的，对人类的生命安全、环境破坏以及资源损失具有严重的威胁作用[1-2]。我国属于发展中国家，国家的发展、人类的生活需求需要消耗大量的矿产资源，对矿山开采的需求日益增加[3-4]。但是部分矿山开采只注重经济效益，导致开采事故日益增多[5]，对矿山地质灾害进行评估可高效实现预防矿山地质灾害的目的，因此需要研究一种新的金属矿山地质灾害评估方法。

目前，国内外已有相关学者进行了相应研究。邓创等[6]提出一种基于风险理论的金属矿山地质灾害评估方法，结合相关环境及地质设定相关联的参数，并量化金属矿山地质发生灾害的概率，结合相关的风险理论指标，完成金属矿山地质灾害评估，该方法的评估耗时较长。贾茜淳等[7]提出一种基于GPS定位的金属矿山地质灾害评估方法，通过量化采集得到的相关数据，将量化数据作为输入因子，灾害等级作为输出因子，构建神经网络模型，完成金属矿山地质灾害评估，该方法评估的准确性较低。

针对以上所述现状及现有方法存在的问题，本文提出了一种基于多级模糊数学的金属矿山地质灾害评估方法。

1 基于多级模糊数学的金属矿山地质灾害评估方法

1.1 多级模糊数学设计

模糊数学主要是描述以及处理不确定性的相关工具，并且具有稳定的数学基础，能够对灾害中的不确定性进行建模，提供直观的方式描述各个风险因素之间的关系。模糊推理结构能够更加充分的反应风险机制的产生[8-9]，它能够有效利用数据库进行数据存储，能够提供快速有效的概率推理方法，并且在风险跟踪中发现新的证据，新数据能够引入相关的模糊数学模型中，重新计算或者更新先前的评估结果。

首先分析金属矿山地质灾害的不确定性特征，构建灾害评估指标体系，设计多级模糊模型，进行主客观定权。具体过程如下：

模糊数学理论可直观的表示为一个复杂的赋值因果关系，一个完整的模糊数学模型是由二元组构成，且B≤G，则有：

·G=(V(G),E(G))。

(1)

式中：·G代表有向无环图，V(G)代表节点集合，E(G)代表弧集合。

依据模糊数学模型结构，确定多级模糊模型[10]：

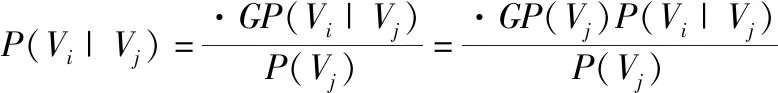
。(2)

式中：P(Vi)代表先验概率，P(Vi|Vj)代表后验概率。在矿山地质灾害中，将矿山地质划分为不同区域，作为不同节点目标，即为评价不同区域的灾害风险指标，风险指标主要是指某一矿山地质风险状态的发生概率[11]；矿山地质灾害风险指标之间存在的因果关系，利用不同区域节点的有向弧表示，地质灾害发生的条件概率充分反映了因果关系的强弱，也就是所谓的概率指标大小；利用先验概率以及后验概率，进行推理计算，确定最终的地质灾害概率后验分布，即为地质区域所处不同状态的概率分布，以概率的表达式充分说明区域矿山地质灾害风险状态。

依据多级模糊模型，整合不同区域风险，并对其进行约束，获取后验概率的表达式：

(3)

通过公式(3)设定先验概率分布以及非根节点概率分布，推理得到包含整体矿山地质的联合地质灾害风险概率分布。

在上述分析的基础上，加入地质灾害根节点的权重参数wi[12]。对后验概率公式进行主客观定权，获取隶属函数表达式为：

L(Vi)=P(v|V1,V2,…,Vk)wi

(4)

1.2 基于模型的矿山地质灾害指标体系设计

在前一小节的基础上，依据主客观定权后的地质灾害风险数学模型，构建金属矿山地质灾害评估模型，利用该模型将金属矿山地质灾害划分为不同的等级，进而完成矿山地质灾害指标体系设计。具体过程如下：

采矿区的面积不断扩大的同时，支撑其覆岩层的矿柱压力也就越来越大[13]，此时矿山地质沉陷系数为：

(5)

式中：H代表开采深度，W代表开采宽度。当沉陷系数达到一定的值时，矿柱就会发生破裂。

在岩层中由于水的冲刷会带走大量的细小颗粒，发生机械腐蚀。随着细小颗粒的不断减少，造成岩层逐渐松散，其孔隙度与强度快速降低，造成大规模的碎屑流，导致颗粒无法均匀的分配在岩层中，矿层渗透压力为：

(6)

式中：h代表颗粒分布差，L代表渗透长度。

岩石颗粒的不断渗透变形对金属矿山造成较大的危险，从而发生事故。滑坡主要是指斜坡的岩体在受重力的作用下沿着任意弱面下滑的地质现象[14-15]。在进行矿山开采以前，边坡岩体应该处于平衡的状态，尾矿的堆积会加大顶部的荷载，造成变形，增大坡度，降低了腐蚀的基准面。此时岩层斜坡的稳定性系数稳定系数为：

(7)

式中：θ代表坡角，φ代表临界坡脚，C·A代表滑坡重力和滑坡之间的接触面积。通过公式(7)可知下滑力的增大会造成山体滑坡的机率增大，下滑力和重力坡角呈正相关。

在开采矿山的过程中，岩石颗粒的渗透产生了大量固体残渣，主要包含弃土等多种物质，是形成泥石流灾害的主要原因[16-17]。在固定的地形地貌条件下，颗粒渗透动力会激发一定的山体滑坡，加快堆积物的流动速度。

在上述分析的基础上，结合主客观定权模型，构建金属矿山地质灾害评估模型，即：

(8)

金属矿山地质灾害等级为：

(9)

有效的金属矿山地质灾害指标为：

Q=Jδ×P(Mp|mp1,mp2,…,mpk)。

(10)

式中：δ表示灾害等级效用因子。P(Mp|mp1,mp2,…,mpk)表示金属矿山地质灾害环境影响因素集合，金属矿山地质灾害发生受众多环境因素的影响，包括动力地质作用、岩土体基本属性、胁迫稳定性、水文地质特征与人类活动强度等，用M1,M2,…,Mp表示，p≤5，每种环境因素包含众多环境因子，表示为mp1,mp2,…,mpk。

综上所述，完成了基于多级模糊数学的金属矿山地质灾害指标设计。

2 实验结果与分析

以我国某矿区为例，对该矿区实行地质灾害评估，判断该矿区地质灾害危险性相关的模糊因素，先设定评价单元与评价因素，然后根据本文提出的多级模糊模型，进行主客观定权，获取隶属函数；将每个参评因子的每项因子根据地质灾害评价因子分级，获取每个因子隶属于相应的评价等级隶属度，最后评估结果根据最大隶属度原则判定。

把地质灾害评估等级设定为危险性高、危险性较高、危险性中度和危险性低4种等级。实验所选取的矿区地质灾害分布情况如表1所示。

表1 实验矿区地质灾害点统计数据

环境因素的设定是该矿区地质灾害准确评估的重中之重。根据野外调查的资料把该矿区地质灾害的环境因素设定为5种，依次是动力地质作用、岩土体基本属性、胁迫稳定性、水文地质特征与人类活动强度。该5种环境因素设定为19个环境因子，由此建立的评价指标和引用贝叶斯网络模型，进行主客观定权后的结果如表2所示。

表2 地质灾害评估因子权值、隶属度计算结果

续表2评估指标(三级)权值环境因子(二级)权值评估内容(一级)权值隶属度水文地质特征0.2基岩孔隙水0.34孔隙裂隙水0.3孔隙水0.3水土流失0.2富水性0.3(0,0.5,0.3,0)埋深0.24(0,0.9,0)矿化度0.34(0,0.2,0.6)富水性0.3(0,0.14,0.84,0)埋深0.24(0,0,2,0)矿化度0.34(0,0,0.1,0.7)富水性0.3(0.04,0.2,0.24,0.5)埋深0.24(0.04,0.2,0.24,0.5)矿化度0.34(0,0,0.1,0.7)地形坡度0.3(0,0,0.2,0.6)沟谷密度0.34(0.1,0.1,0.1,0.3)植被覆盖率0.24(0,0.1,0.1,0.5)人类活动强度0.2人工填土0.2水质污染0.15填土分类0.34(0.5,0.1,0.2,0.2)厚度0.3(0.5,0.1,0.2,0.2)面积0.24(0.5,0.1,0.2,0.2)五毒含量0.24(0.2,0.2,0.1,0.5)硬度0.1(0.2,0.2,0.1,0.5)NO-40.24(0.2,0.2,0.1,0.5)NO-30.1(0.2,0.2,0.1,0.5)SO2-40.2(0.2,0.2,0.1,0.5)

根据表2数据，通过最大隶属度原则，对该矿区的每个环境因子实行地质灾害等级综合评价，结果如下。

(1)一级评估

将矿区地质灾害综合评估结果矩阵用A表示，表示非相同质量级别的隶属度：

A11=[0,0.46,0.52,0] ；

(11)

A12=[0,0.05,0.33,0.5]；

(12)

A13=[0.08,0.65,0.18,0.05]；

(13)

A21=[0.21,0.45,0.14,0.14] ；

(14)

A23=[0.54,0,0.44,0]；

(15)

A24=[0.3,0,0.5,0]；

(16)

A25=[0.234,0.364,0.1,0.1]；

(17)

A26=[0.62,0.13,0.17,0.04]；

(18)

A31=[0.11,0.21,0.29,0.35]；

(19)

A33=[0.014,0.184,0.25,0.53]；

(20)

A34=[0.016,0.382,0.30,0.28]；

(21)

A41=[0,0.40,0.30,0.27]；

(22)

A42=[0,0.01,0.5,0.37]；

(23)

A43=[0.032,0.064,0.331,0.56]；

(24)

A51=[0,0.04,0.334,0.614]；

(25)

A52=[0.4,0.24,0.1,0.04]；

(26)

A53=[0.04,0.1,0.24,0.4]。

(27)

(2)二级评估

A1=[0.2,0.38,0.39,0.2]；

(28)

A2=[0.37,0.33,0.1,0.07]；

(29)

A3=[0.05,0.33,0.33,0.25]；

(30)

A4=[0.012,0.260,0.28,0.435]；

(31)

A5=[0.194,0.124,0.2,0.37]。

(32)

(3)三级评估

A实验矿区=[0.30,0.15,0.24,0.37]。

(33)

实验矿区地质灾害综合评估结果矩阵设成A实验矿区。把地质灾害情况用隶属度区间的形式进行判断，实验将隶属度区间设定为：

低级：[0.8,1.0]；

中级：[0.5,0.8]；

较高级：[0.2,0.5]；

高级：[0,0.2]。

计算最终评价结果，取各级中间值设成模糊子集，则模糊子集 ，实验矿区地质灾害最终评价结果设成G:

G=(0.8×0.302+0.64×0.152+0.34×0.242+0.2×0.372)/(0.302+0.152+0.242+0.372)≈0.43。

(34)

则该矿区的地质灾害危险性等级为较高。

综合上述一级评估、二级评估和三级评估的分析，可以看出利用本文的评估模型能够明确的划分出地质灾害等级，验证了方法的可行性，表明其能够有效的完成矿山地质灾害指标体系设计。

3 结束语

针对传统方法存在的一系列问题，设计多级模糊数学模型，在金属矿山地质灾害评估中应用。分析金属矿山地质灾害的不确定性，构建相应的评估体系。划分出不同的灾害等级。实验结果表明，本文给出的方法能够有效降低灾害评估时间，提高灾害评估效率，使获取的灾害评估结果更为准确。

总体分析，当前的金属矿山地质灾害评估的研究主要属于自然灾害。虽然全面考虑了导致灾害发生的灾害风险评估体系已经建立，但是进展却不是十分的明显。在灾害损失的评估中，针对直接造成的经济损失的评估方法当前发展较为成熟，但是间接造成损失的评估还不是十分完善。未来阶段，需要进一步完善金属矿山地质灾害评估体系，及时采取相应的保护措施，进一步减少经济损失。