复杂气井井筒完整性量化分级评价方法
刘铭刚,王廷春,李 勇,逄铭玉,万古军
(1.中国石油化工股份有限公司青岛安全工程研究院,山东 青岛 266100;2.中国石油化工股份有限公司青岛安全工程研究院化学品安全控制国家重点实验室,山东 青岛 266100)
0 引 言
井筒完整性(wellbore integrity,WI)评价技术的研究始于1977年英国石油公司(BP)建立的油气井完整性管理体系,其于1980年确立了以完井技术为核心的油气井完整性管理方法,提出并阐明了油气井完整性工程师岗位对油气田开发的重要性[1]。
2010年“深水地平线事件”后,各油气资源大国、油气开发企业和技术服务公司等吸取教训,开始重视油气井井筒完整性的技术开发和科学研究。挪威石油工业协会牵头成立由英国石油公司(BP)、康菲石油公司(Conoco Phillips)、埃尼挪威公司(Eni Norge)、埃克森美孚(Exxon Mobil)、Marathon Oil、Nexen Inc.、挪威壳牌公司(Norske Shell)、挪威国家石油公司(Statoil)、道达尔(Total)等石油技术服务的龙头企业组成工作团队,负责编写井筒完整性标准《OLF Commended Guidelines for Well Integrity》,2011年挪威石油工业协会完成对Norsok D-010标准《Well Integrity in Drilling and Well Operations》的更新。2011年,美国石油学会发布API96《Deepwater Well Design and Construction》,其中对油气井设计和钻井建井中的井筒完整性提出了比较规范的概念和技术条款。2013年,挪威石油工业协会对上述两部井筒完整性的主要标准进行了修改和增补,将“油气井井筒完整性”定义为采用有效的技术、优化的设计及合理的管理模式来降低运行风险,保证油气井在达到废弃前的运行周期内的安全可靠性;API标准将“油气井井筒完整性”定义为采用技术、操作和管理措施,使得油气井井筒在整个生命周期中保持稳定的、正常的流体注入状态和采出状态[2]。
“井筒完整性”概念的提出为油气井井筒设计和安全评价的综合研究提供了方向,而完整性分析最重要的内容是建立有效的可靠性评价方法。现行的工程结构设计方法多以名义值或最大值作为可靠性评价的依据,如API 5C5、ISO 10400、SY/T5724等[3]。但对复杂油气井,如普光气田的超深高温高含硫气井,其井筒结构是由油管、套管、水泥环、地层和胶结面等组成的多层有机整体,该类井筒的完整性无法用某个单一的名义值来评价。目前针对井筒完整性的评价方法存在以下问题:由于计算模型复杂导致考虑的可靠度指标过少;没有考虑参数之间的相关性,导致计算变量过多,造成计算过程繁琐复杂。如图1所示的复杂气井井筒结构,为对其完整性进行评价,除对各组成结构或部分的强度进行校核外,可以将整个复杂结构作为一个系统进行可靠性分析和失效概率计算。因此本文基于可靠性理论,提出一种适用于复杂气井井筒完整性评价的量化和分级方法。
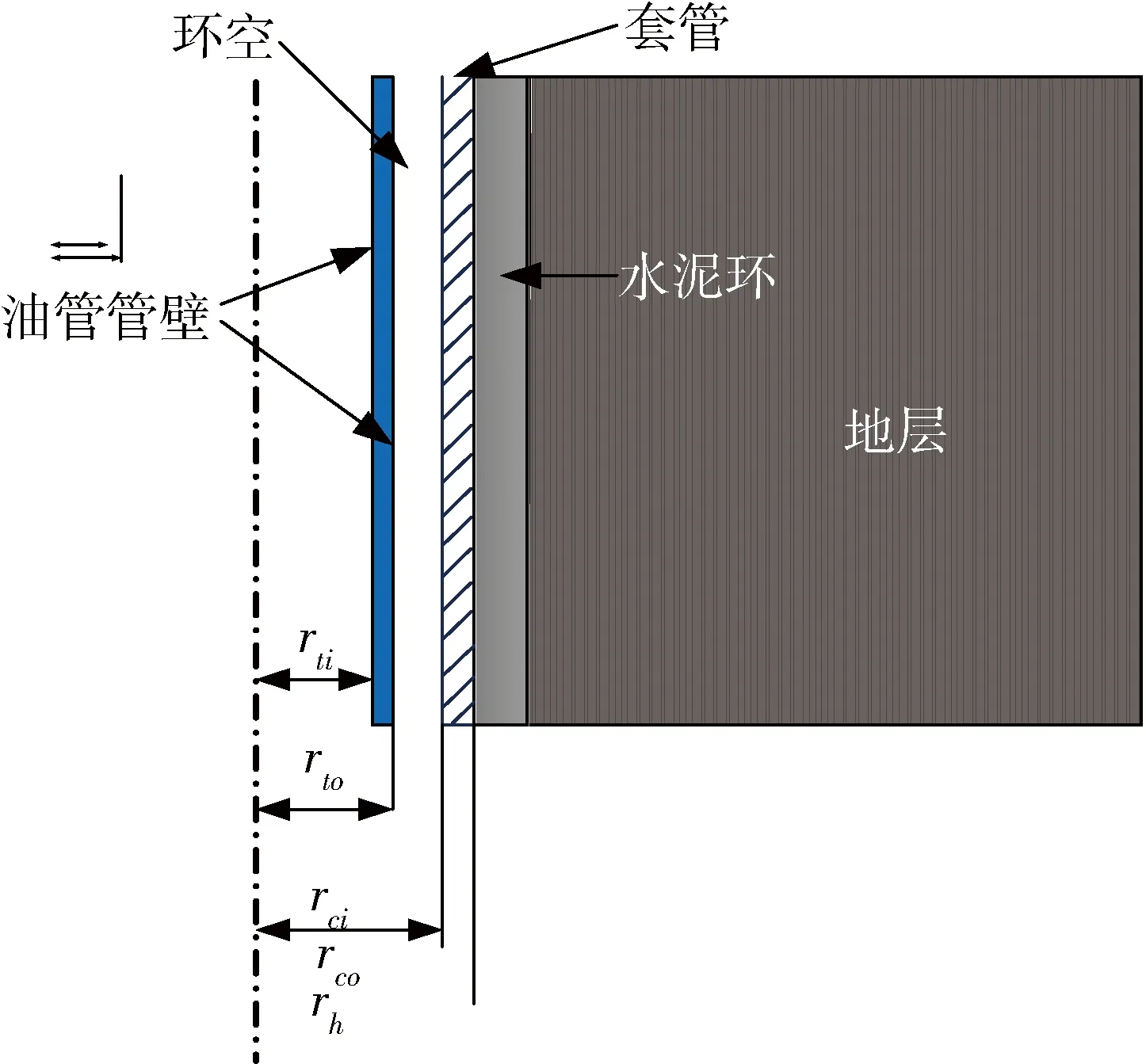
图1 复杂气井井筒结构示意图Fig.1 Schematic diagram of wellbore structures in complex gas well
1 基于中心点法的井筒完整性评价原理
对复杂气井井筒来说,其可靠性取决于整个生产、作业过程中的井筒结构完整性。根据已有研究可知,与井筒完整性有关的不确定性参数都符合正态分布,因此可以定义服从正态分布的可靠性指标β,其与井筒完整性失效概率及可靠概率的关系见式(1)[4]。
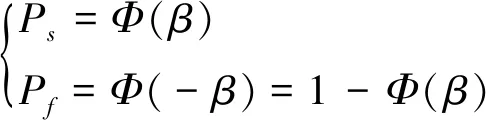
(1)
式中:Φ()为标准正态分布函数;Ps为可靠概率,表示井筒完整性保持良好的概率;Pf为失效概率,表示发生井筒完整性失效事件的概率。存在关系见式(2)。
Ps+Pf=1
(2)
定义井筒完整性的状态函数见式(3)。
Z=g(X1,X2,…,Xn)
(3)
式中:Xi为对状态函数的贡献因素,其平均值为μXi,i=1,2,3……n;g(Xi)为状态函数的计算函数,对井筒完整性参数来说,定义g(Xi)为各结构的剩余强度,即失效强度与实际强度之差[5-6]。
将式(3)在每个贡献因素Xi的均值μXi处展开成Taylor形式,见式(4)。
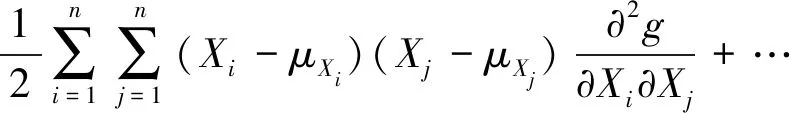
(4)
省略高阶项,式(4)简化为式(5)。
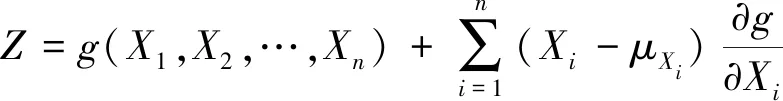
(5)
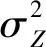
μZ=E(Z)=g(μX1,μX2,…,μXn)
(6)
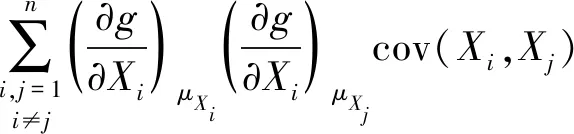
(7)
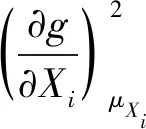
式(7)中,如果贡献因素项Xi(i=1,2,3……n)是相互间线性无关的,则式(7)化简为式(8)。
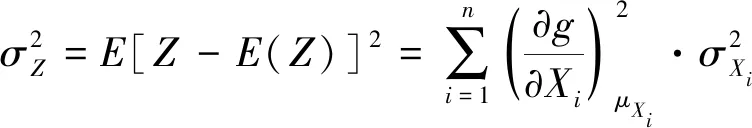
(8)
则可靠性指标β用μZ和σZ表示为式(9)。
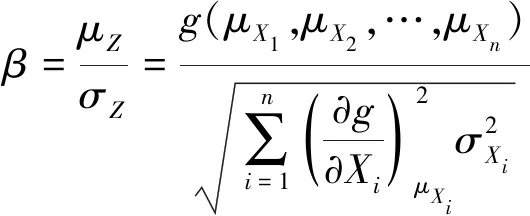
(9)
进而失效概率Pf可由式(10)求得。
Pf=Φ(-β)=1-Φ(β)
(10)
2 基于Monte-Carlo法的井筒完整性评价原理
当处理结构复杂、失效贡献因素众多的问题时,上述方法存在人工计算量庞大的问题。利用数值软件,如ANSYS软件,基于Monte-Carlo法可以计算用结构或力学参数作为井筒完整评价指标的可靠性问题[7]。Monte-Carlo法是一种基于事件抽样的概率分析方法。在复杂的事件系统中,Monte-Carlo法通常是检验概率计算结果准确性的唯一方法[8-10]。
Monte-Carlo法计算井筒完整性失效概率的步骤如下所述。
1) 通过统计或其他方法获取井筒完整性失效的贡献因素Xi(i=1,2,3…n),及每个贡献因素的概率分布。
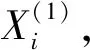
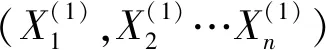
4) 判断N个随机数Z(1),Z(2)…Z(N)里面是否满足以下条件,即存在M(M≤N)个随机数Z(i)(1≤i≤M),满足Z(i)<0,则在抽样次数足够多(N足够大)的情况下,根据大数定理可知井筒完整性的失效概率见式(11)[11-12]。
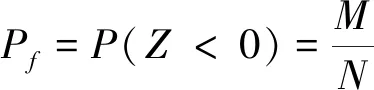
(11)
5) 拟合Z的概率分布曲线,进而得到状态函数的平均值μZ和方差σZ,利用式(12)、式(13)和式(14)即可求得井筒完整性的可靠性指标β、失效概率Pf和可靠概率Ps。

(12)
Pf=1-Φ(β)
(13)
Ps=Φ(β)
(14)
根据因子分析结果可知,复杂井筒的各结构对“井筒完整性失效”这一项事件的贡献因素重要度排序为:油管轴向应力、套管等效应力、水泥环切应力、第一胶结面切应力、第二胶结面切应力和地层切应力。可靠度计算时,仅需对上述6个最重要的贡献因素进行概率计算。假设上述6个贡献因素对应的失效事件互相独立,则根据Bayes定理求得最终的井筒系统可靠概率见式(15)[13]。
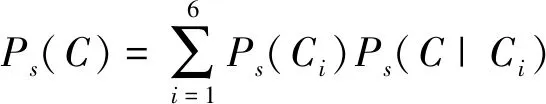
(15)
式中:C为井筒完整性良好的事件;Ci为贡献因素;Ps(C)为井筒完整性良好的事件的发生概率;Ps(Ci)为贡献因素的重要度大小;Ps(C|Ci)代表贡献因素Ci发生C事件的概率。
3 工程实例
3.1 基于中心点法的井筒可靠性概率计算
以T4为算例,取井深分别为800~900 m、1 100~1 200 m和1 800~1 900 m的储层所在井段进行井筒完整性评价,井筒各结构的确定性参数见表1。
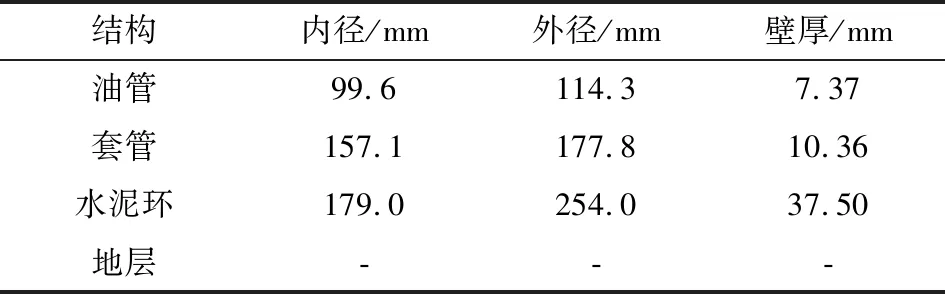
表1 T4储层井段确定性参数统计结果Table 1 Statistical results of deterministic parameters in T4
选取油管轴向应力、套管等效应力、水泥环切应力、第一胶结面切应力、第二胶结面切应力和地层切应力6项作为复杂气井井筒完整性的状态函数Z的贡献因素,利用中心点法计算得到每个贡献因素对应的可靠性指标β及概率的分布见表2和图2。
从表2和图2中可以看出,在800~900 m井段,第一胶结面的可靠概率最低,为0.826,地层的可靠概率最高,为0.989;在1 100~1 200 m井段,第一胶结面的可靠概率最低,为0.822,地层的可靠概率最高,为0.980;在1 800~1 900 m井段,套管的可靠概率最低,为0.797,地层的可靠概率最高,为0.886。说明在井深较小的井段,第一胶结面是引起井筒完整性失效最可能的因素;随着井深的增加,因套管失效而造成井筒完整性失效的概率将逐渐增大。此外还可以看出,水泥环和胶结面的可靠概率在6项贡献因素中排名相对较低,是复杂气井设计和作业中应重点注意的因素。
表3为40次井筒事故中井筒完整性失效的贡献因素与失效次数统计情况,根据前文提到的Bayes定理,计算T4井筒完整性的可靠概率见式(16)。
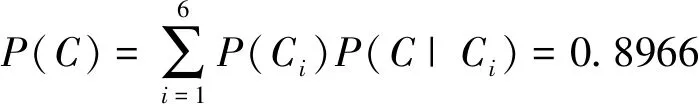
(16)
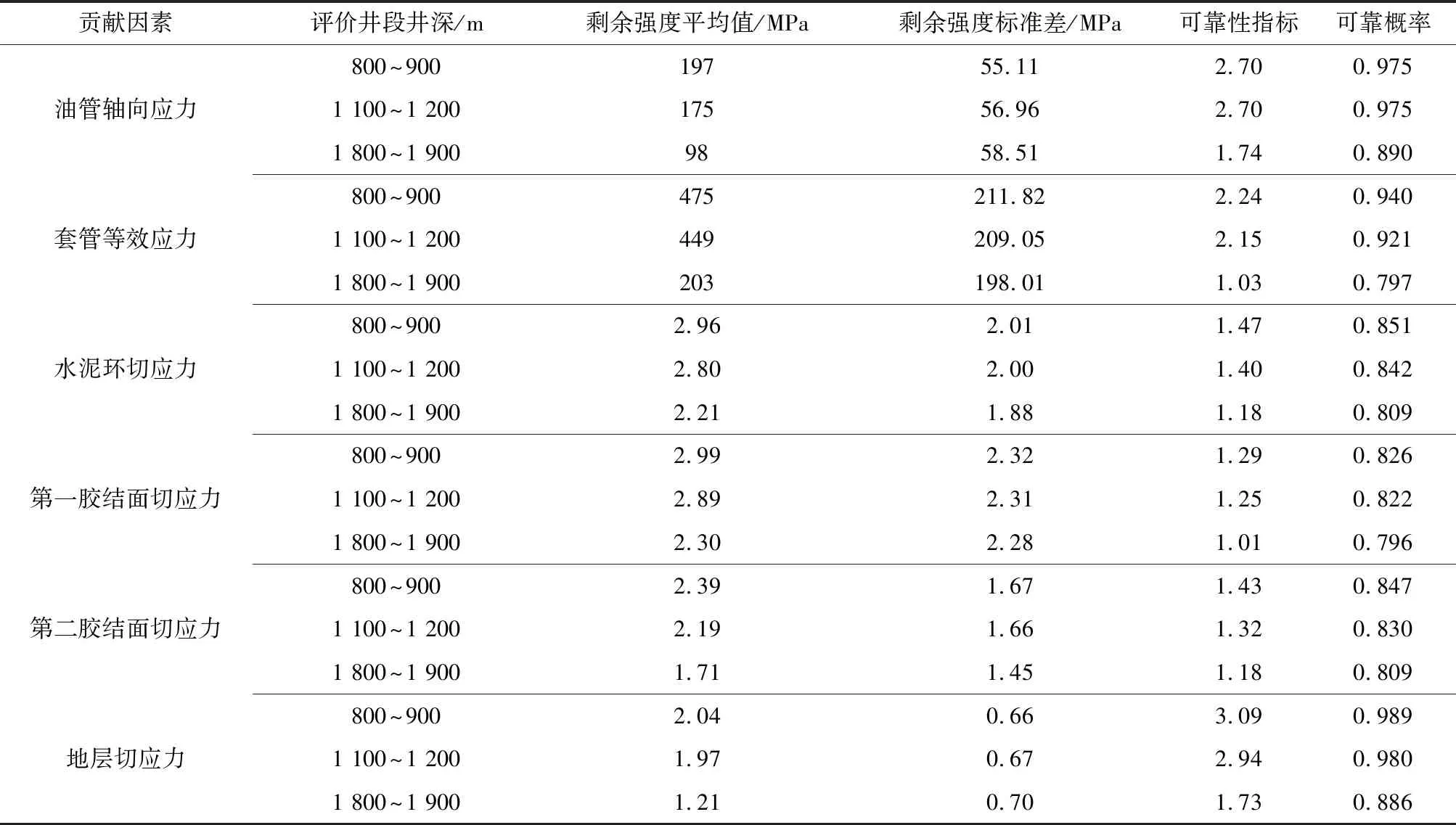
表2 T4井筒完整性的可靠性指标和可靠概率计算结果(中心点法)Table 2 Calculation results of reliability indexes and reliable probabilities for wellbore integrity in T4 (center-point method)
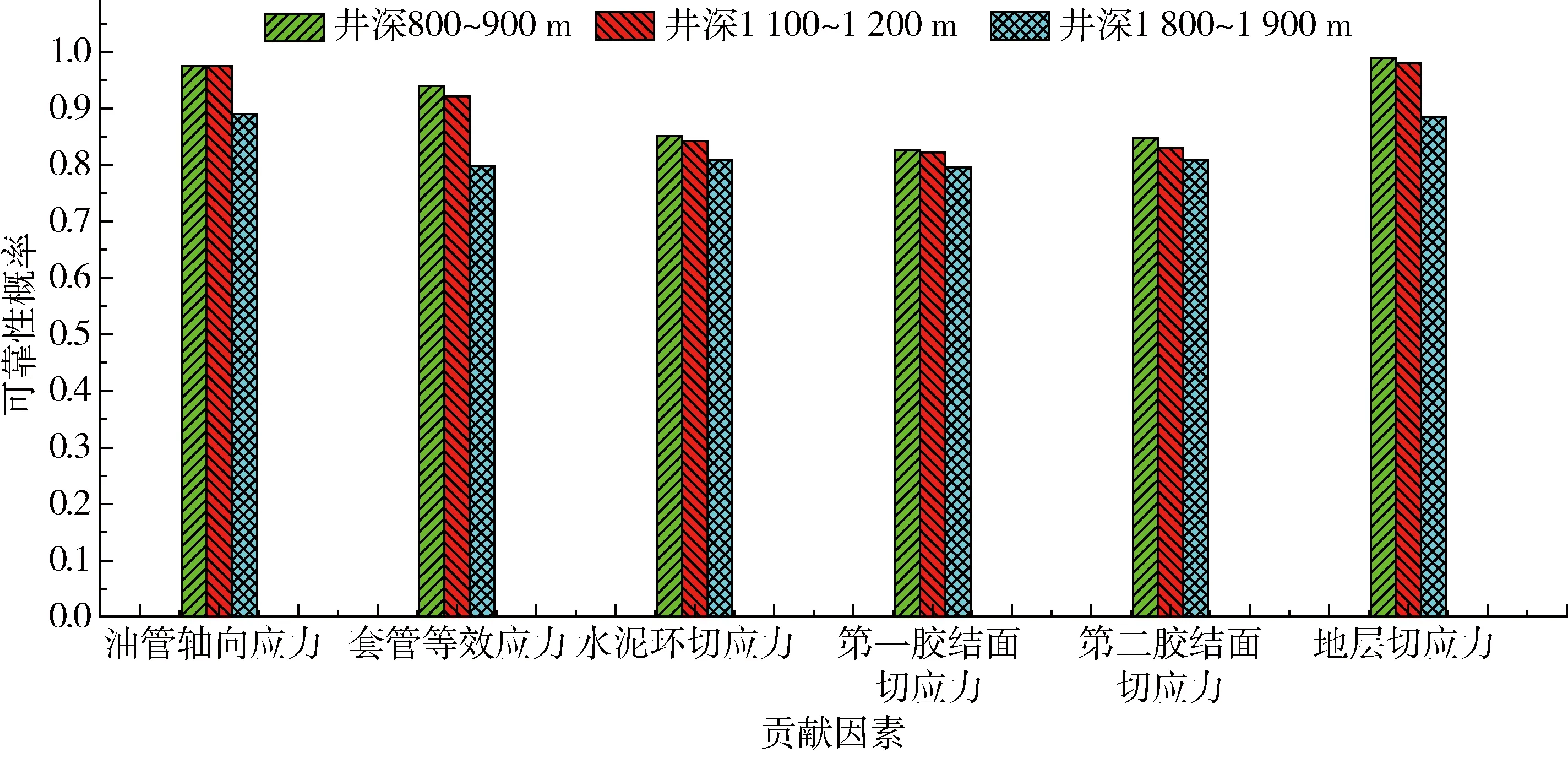
图2 T4井筒完整性的可靠概率与失效贡献因素的关系(中心点法)Fig.2 Correlation of reliable probabilities and failure contributing factors of wellbore integrity in T4(center-point method)
3.2 基于Monte-Clarlo法的井筒可靠性概率计算
为验证中心点法计算结果的准确性,将T4井筒各结构的6个贡献因素对应的名义值(即各结构的强度计算结果)输入ANSYS概率分析模块,对每个目标井段进行10次Monte-Carlo法抽样,得到106组贡献因素组合。当任意结构的实际计算强度大于失效强度时,即判定井筒完整性失效,反之则井筒完整性可靠[11-12]。得到的状态函数值(可靠度指标)与其对应的概率密度曲线如图3~8所示。

表3 T4井筒完整性失效的贡献因素与失效次数Table 3 Contributing factors and failure times of wellbore integrity failure in T4

图3 油管可靠性状态函数的概率密度曲线Fig.3 Probability density of reliability state function of tubing
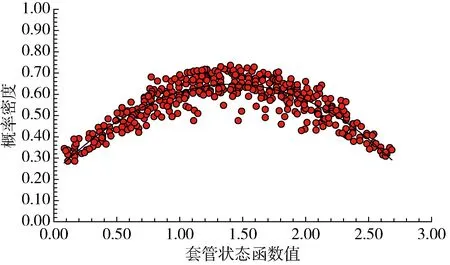
图4 套管可靠性状态函数的概率密度曲线Fig.4 Probability density of reliability state function of casing
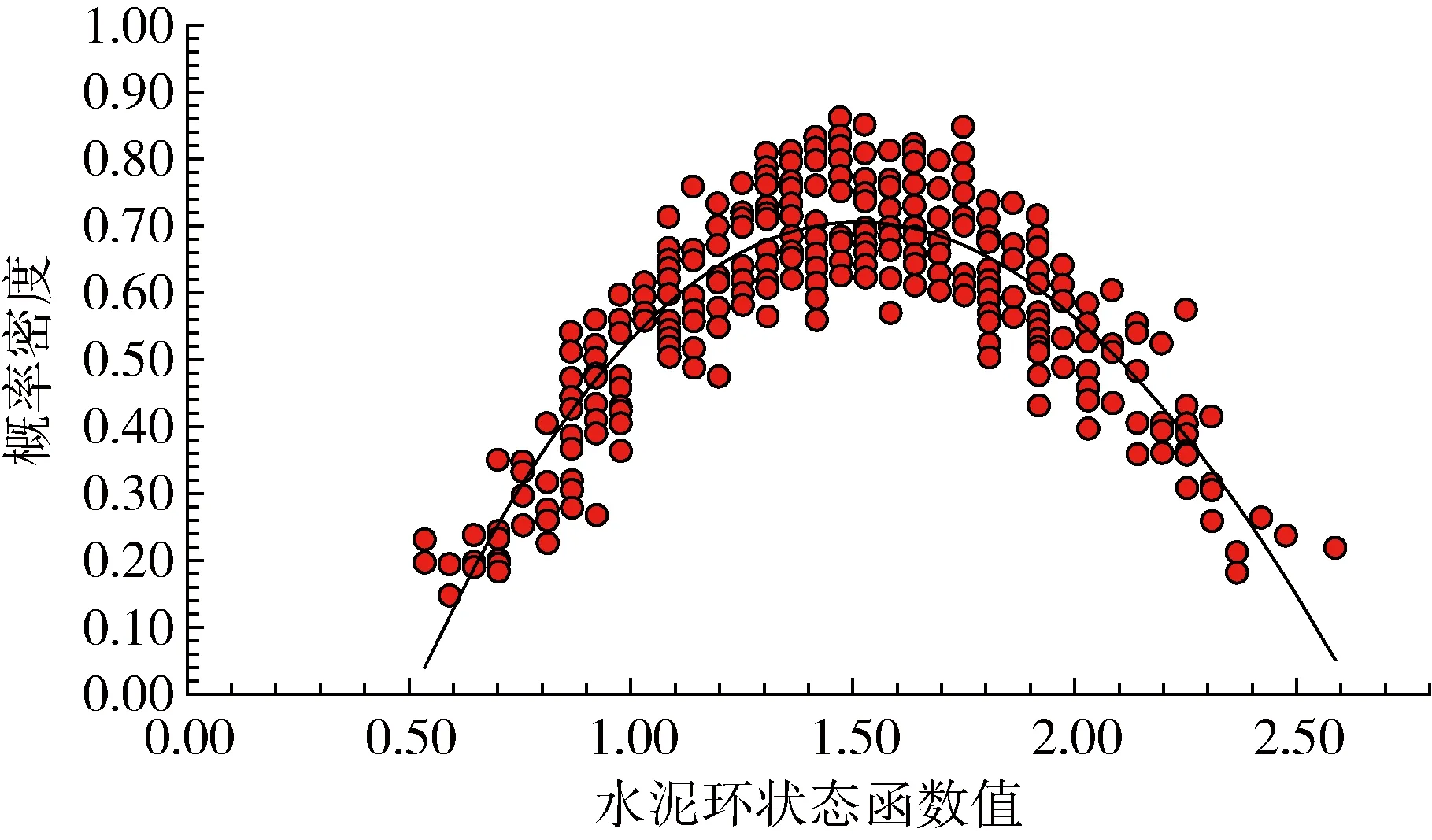
图5 水泥环可靠性状态函数的概率密度曲线Fig.5 Probability density of reliability state function of cement
通过对上述概率密度曲线的拟合,得到每个贡献因素对应事件平均值和方差,从而得到Monte-Carlo法计算的可靠性指标β及概率的分布,分别见表4和图9。根据Bayes定理,计算T4井筒完整性的可靠概率见式(17)。
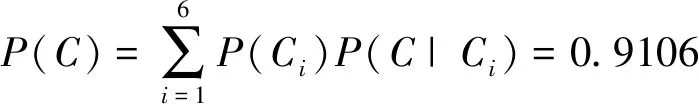
(17)
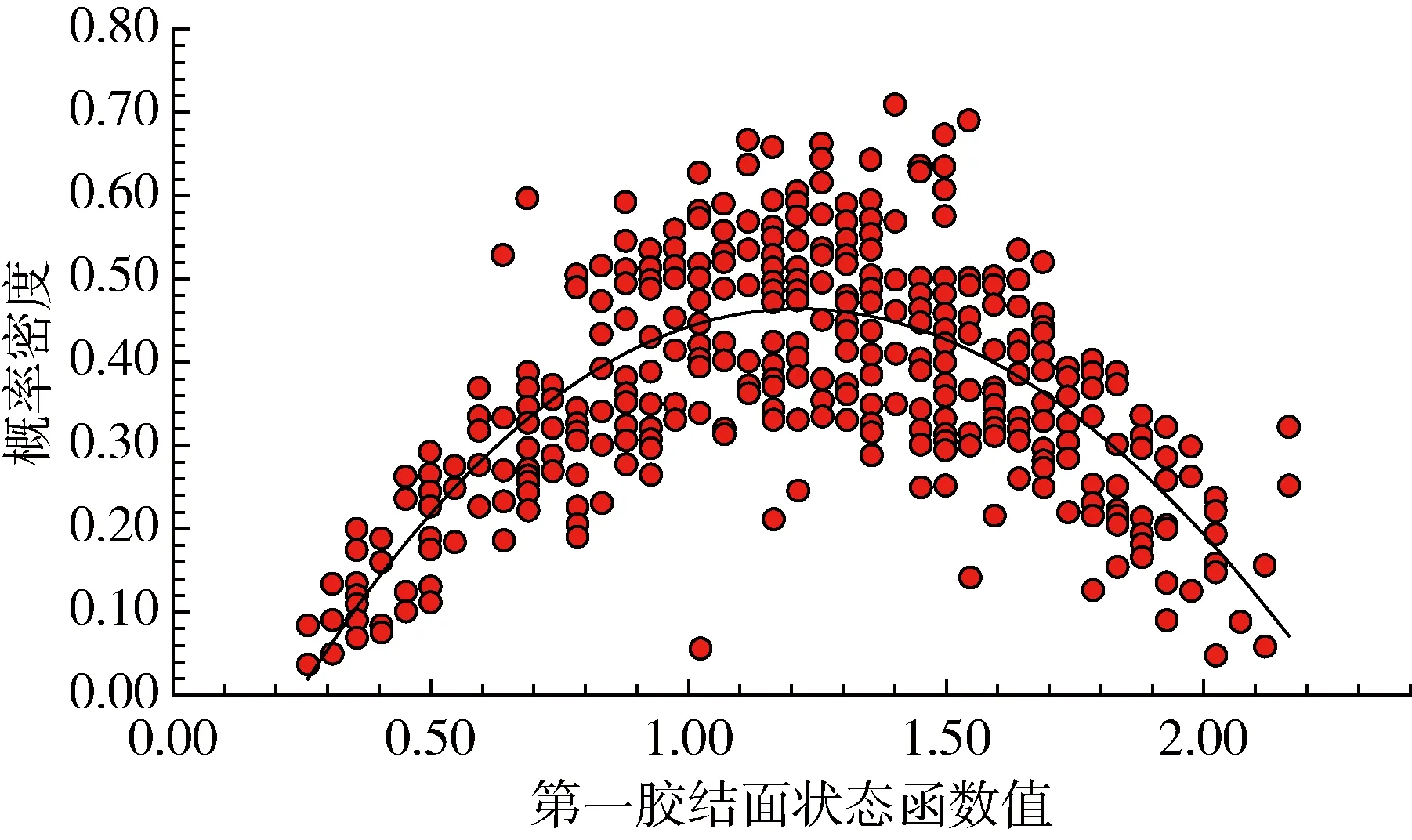
图6 第一胶结面可靠性状态函数的概率密度Fig.6 Probability density of reliability state function of 1st cemented interface
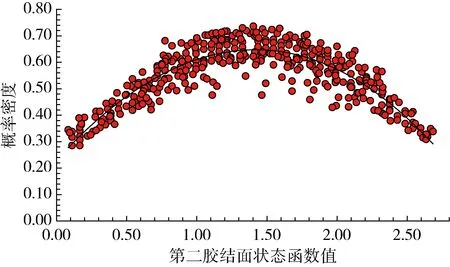
图7 第二胶结面可靠性状态函数的概率密度Fig.7 Probability density of reliability state function of 2nd cemented interface
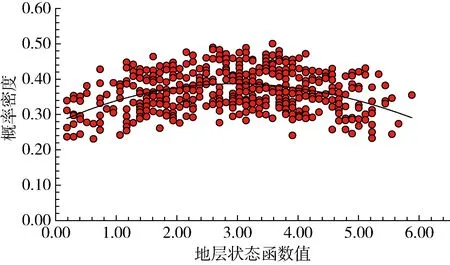
图8 地层可靠性状态函数的概率密度Fig.8 Probability density of reliability state function of stratum
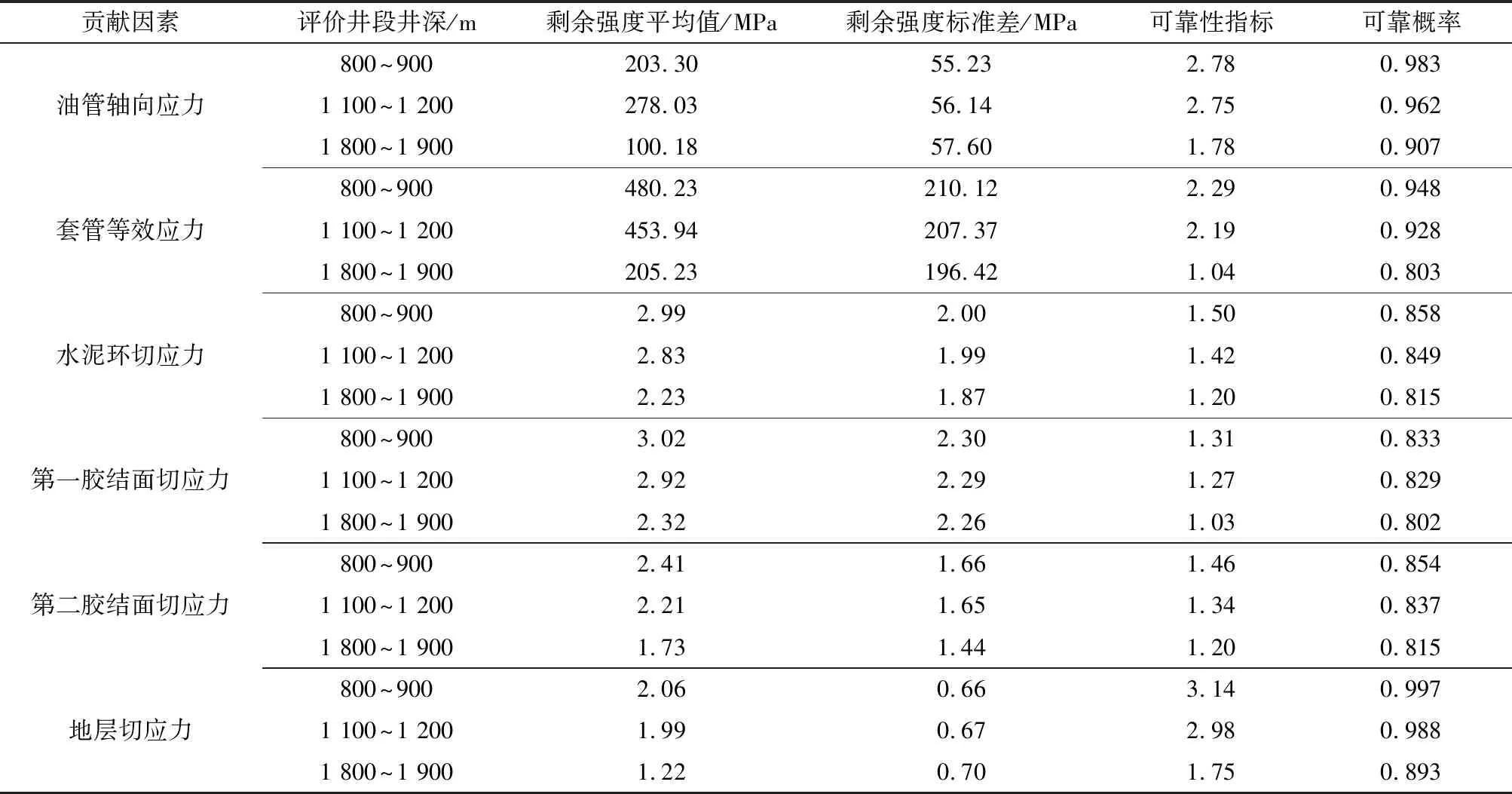
表4 T4井筒完整性的可靠性指标和可靠概率计算结果(Monte-Carlo法)Table 4 Calculation results of reliability indexes and reliable probabilities for wellbore integrity in T4 (Monte-Carlo method)
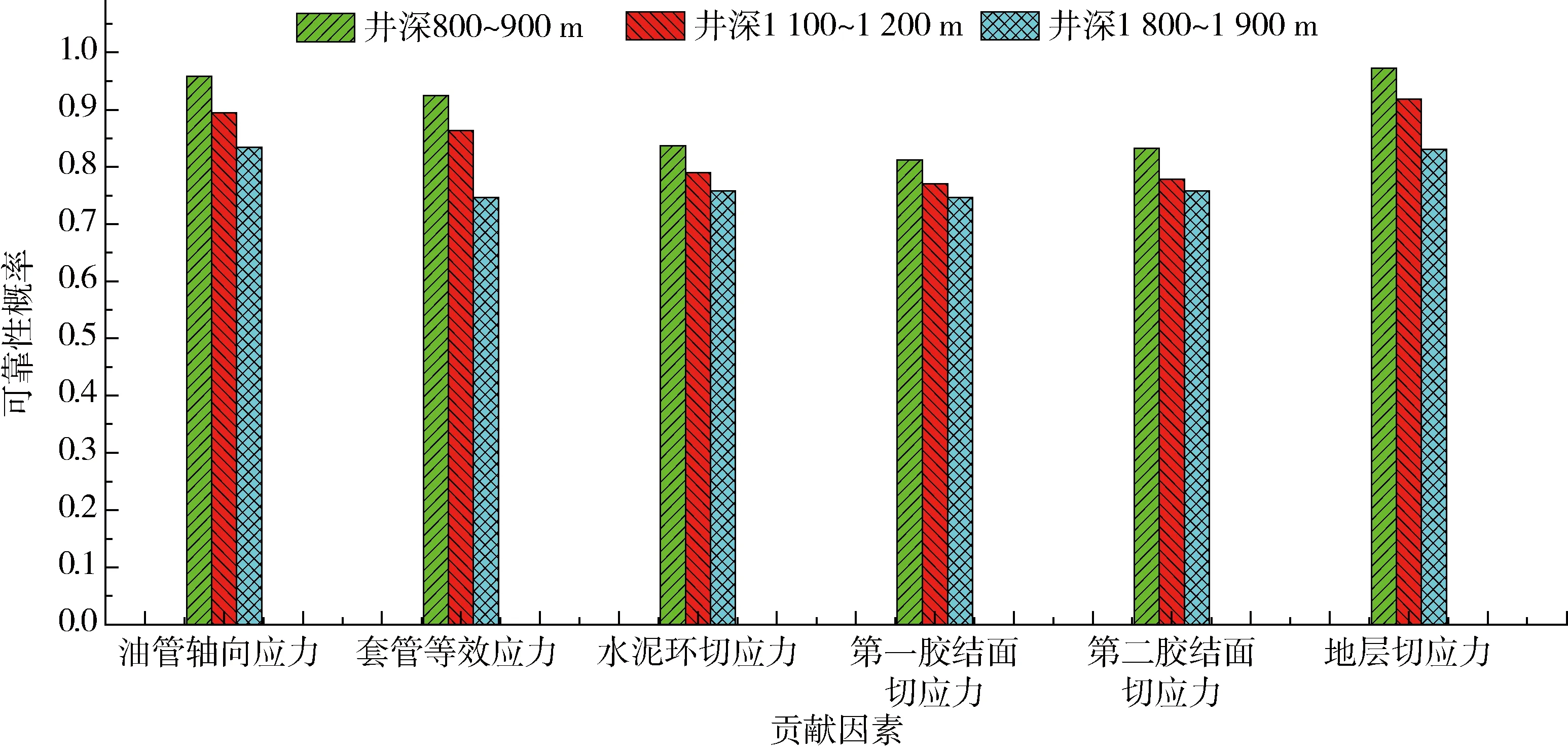
图9 T4井筒完整性的可靠概率与失效贡献因素的关系(Monte-Carlo法)Fig.9 Correlation of reliable probabilities and failure contributing factors of wellbore integrity in T4 (Monte-Carlo method)
可以看出,Monte-Carlo法计算的可靠性指标和概率与中心点法的结果比较吻合,可靠概率的计算误差仅为1.54%,说明本文建立的井筒完整性的可靠度计算方法是准确可行的。
3.3 两种方法结果对比
定义可靠概率0.90 图10 T4井筒完整性的分级结果Fig.10 Grading results of wellbore integrity of T4 1) 基于中心点法推导了复杂气井井筒完整性可靠概率计算公式,并通过建立“井筒完整性可靠概率”与“井筒可靠性指标”之间的关系,提出了井筒完整性的分级评价标准,定义可靠概率0.90 2) 通过将中心点法与Monte-Carlo法进行对比,证明了中心点法精度良好,并具有工程适用性。以T4为例,中心点法和Monte-Carlo法计算得到的井筒完整性可靠概率分别为0.8966和0.9106,井筒完整性的评价结果分别为“较可靠”和“很可靠”。 3) 后续应加强对完整性失效贡献因素不确定性分析方法的研究,考虑其随机分布规律,进而引入更多相关参数,如时间、管柱材料的超低周疲劳和地层蠕变等。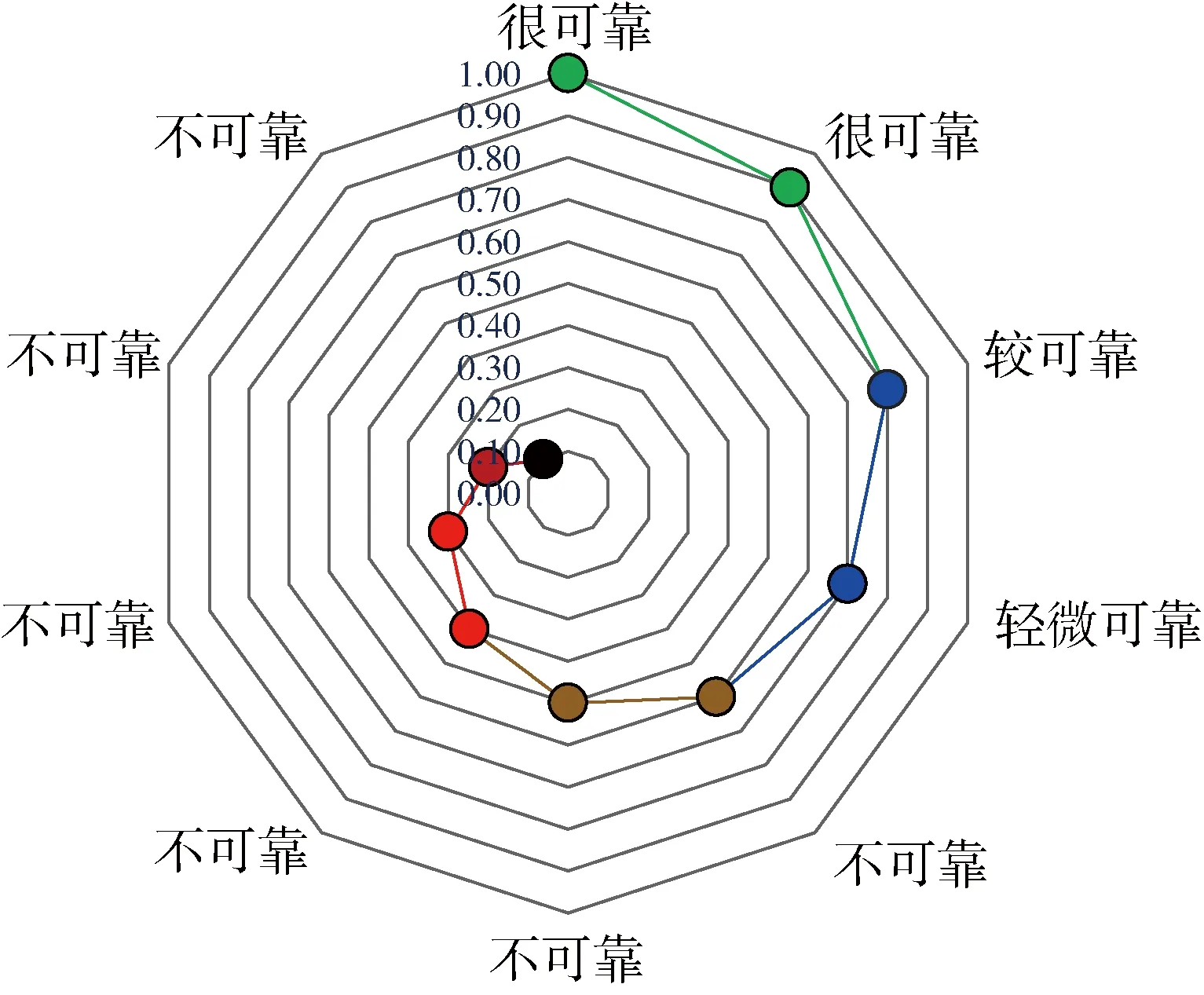
4 结论及建议

