SCE标定结合EnKF同化遥感和WOFOST模型模拟冬小麦时序LAI

许 伟，秦其明，张添源，龙泽昊

SCE标定结合EnKF同化遥感和WOFOST模型模拟冬小麦时序LAI

许 伟，秦其明※，张添源，龙泽昊

（北京大学遥感与地理信息系统研究所，北京 100871）

WOFOST（world food studies）模型可用于模拟冬小麦全生育期内的时序叶面积指数（leaf area index, LAI），各器官生物量以及最终产量，对冬小麦的长势监测与产量预估有着重要意义。但将WOFOST模型用于中国具体区域的冬小麦生长模拟时，存在着参数定标困难、模拟结果不够准确等严重问题。目前对该模型的定标大多依靠研究者的经验进行，虽已总结出了一套从标定到模拟应用的研究方法，但在区域模拟时仍然存在很多问题。为此，该文以较易获取的LAI为参考指标，结合潜在生长水平模式下的WOFOST模型在衡水地区的应用，提出了一种“区域优化标定，像元同化修正”的研究方法：首先在区域尺度上对WOFOST模型进行优化标定，利用扩展傅里叶幅度灵敏度检验法（extend fourier amplitude sensitivity test, EFAST）分析模型各个参数的敏感性，在此基础上选择了可以迅速找到全局最优解的SCE（shuffled complex evolution）算法对总敏感度最高的5个参数进行优化，并将优化前后的时序LAI曲线进行对比；其次运用第一步确定的模型最优参数，在对区域内每个像元进行模拟时，结合Sentinel-2卫星数据反演所得的各个像元LAI，利用集合卡尔曼滤波（ensemble kalman filter, EnKF）在像元尺度上对LAI进行同化修正，并结合采样点的2次实测LAI数据对同化所得结果进行验证。试验发现，优化标定后的WOFOST模型模拟所得LAI曲线更接近所给的LAI真值，在此基础上结合数据同化模拟得出的衡水地区每个像元LAI的2达到0.87，RMSE仅为0.62。因此，与原来只能通过经验进行定标的方法相比，该方法有效地解决了WOFOST模型在具体应用中亟待解决的复杂标定问题，并且结合同化修正有效地提高了模型在各个像元的模拟精度，2由0.70～0.83提升至了0.87，RMSE由0.89～1.36降低至了0.62。同时该文也提供了从模型标定到具体模拟整个过程中各个环节的思路与方法，有利于促进WOFOST模型在区域尺度上的应用。

模型；遥感；冬小麦；时序LAI；WOFOST；SCE

0 引 言

小麦作为中国三大粮食作物之一，在农业生产中有着不可替代的地位，而叶面积指数（leaf area index，LAI）作为小麦生长过程中的一个重要参数，体现了小麦光合、呼吸和蒸腾作用等生物物理过程的能力，与小麦的生长动态以及生态系统生产力密切相关[1-2]。因此准确高效地获取小麦LAI及其动态变化信息对小麦的长势监测与产量预估具有重要意义[3]。

获取小麦LAI的方法一般有4种。第一种是利用仪器进行实地测量，如由美国LI-COR公司生产的LAI2000型植物冠层分析仪。实地测量的LAI数据准确度高，但是只能定点定时测量，难以获取一定空间尺度和长时间序列的LAI数据。第二种方式是利用遥感数据，通过建立小麦光谱反射率与LAI的定量关系，反演得到小麦LAI，一般分为经验模型和物理模型。经验模型的本质是通过建立光谱反射率与LAI的回归关系来进行LAI的反演[4]；物理模型则以辐射传输模型为基础，通过分析电磁辐射在植被冠层内部的传输与交互作用，找到植物参量与冠层反射率之间的物理关系[5]，目前最常用的是PROSAIL模型[6]。利用遥感反演的手段可以快速高效地获取大面积的小麦LAI，但是由于卫星重返周期以及天气的限制，难以获取小麦全生育期的时序LAI。第三种方式是利用作物生长模型结合研究区的天气数据，模拟小麦全生育期的生长状况，进而可以得到小麦全生育期的LAI，常用的有WOFOST（world food studies）模型[7]。但一般模型参数众多，在特定区域使用前必须进行本地化。第四种方式则是在作物生长模型模拟的基础上，结合地面实测数据或者卫星遥感数据进行数据同化。同化常用的方法有优化法[如四维变分法（four-dimensional variational data assimilation, 4DVar）[8]]、滤波法[如卡尔曼滤波（kalman filter, KF）[9]]等，通过最小化观测值与模拟值之间的差异，修正所得的时序LAI曲线，使得模拟结果更加准确。

本文选择潜在生长水平模式的WOFOST模型结合气象站提供的每日最高与最低气温数据和日照数据模拟衡水地区冬小麦的生长，以获得小麦全生育期的时序LAI。如前文所述，本研究开展的关键是对模型的参数进行标定使其适用于衡水地区冬小麦生长的模拟，针对这方面的研究，国内外学者已经开展了很多工作。张素青等[10]在河南省夏玉米主产区对WOFOST模型进行了校准和验证。黄健熙等[11]根据经验将模型参数划分为敏感参数与非敏感参数，敏感参数通过农气站点记录的作物与环境参数计算取值范围，再通过优化法确定，非敏感参数则采用默认值或查阅相关文献得到。何亮等[12]利用扩展傅里叶幅度灵敏度检验法（extend fourier amplitude sensitivity test, EFAST）[13]分析了WOFOST模型各个参数的敏感性，再利用马尔科夫蒙特卡洛方法（markov chain monte carlo，MCMC）对这些敏感参数进行优化。可以看出，现有工作中对WOFOST模型参数标定大多数根据经验进行的，在优化敏感参数的过程中也未采取科学高效的优化算法，主观性较大。何亮等采用的EFAST可以较好地得到模型各个参数的敏感性，但MCMC优化算法依赖于初值的选取，难以收敛。

一般来说，当研究区域内的农作物属于同一品种时，WOFOST模型的参数是唯一确定的，在此情况下每个像元若采用不同的参数反而是不合理的，也即研究区域内的每个像元共用同一套标定后的模型参数。但在每个像元内的作物生长可能由于土壤、水分、播种期等条件的不同而有一定的差异，仅利用同一套参数的潜在水平下的WOFOST模型结合气象数据对作物的生长进行模拟在不同的像元可能存在着一定的偏差。针对此问题，范丽颖[14]在利用经验知识将WOFOST模型进行标定的基础上，利用了集合卡尔曼滤波（ensemble kalman filter, EnKF）[15]方法对LAI的模拟进行同化，以此来提高LAI的模拟精度。但其WOFOST模型的标定仅仅是依靠人为的经验判定，可能会引入较大的误差。

因此，综合以上WOFOST模型在实际应用中的问题，本文提出一种“区域优化标定，像元同化修正”的研究方法。首先，针对WOFOST模型过程中过于依赖人为经验的问题，本文先通过EFAST全局敏感性分析得到模型敏感性最大的5个参数，再利用了SCE（ShuffledComplexEvolution）[16]优化算法结合研究区域单个站点的观测数据对这5个参数在相关研究者们探索出的大致取值范围内进行了优化，从而实现模型的标定，标定后的参数则会被应用于整个研究区域进行作物生长的模拟。其次，为了进一步提高模型模拟的精度，在模型标定的基础上，本文结合Sentinel-2[17]卫星数据反演得到几个特定日期每个像元的LAI值，运用EnKF对模型在每个像元的模拟进行数据同化，以修正由于不同像元的环境差异对作物生长带来的不同影响，由此得到衡水地区冬小麦全生育期的LAI。

1 研究区与数据来源

1.1 研究区概况

本文以河北省衡水市作为试验区。衡水市位于河北省东南部（115°0′－116°34′E，37°03′－38°23′N），占地面积约8 815 km2。衡水市平均海拔约为21 m，西南部地势较高，东北部地势较低，属于大陆季风气候区。衡水市共包括2个市辖区（桃城区、冀州区），1个县级市（深州市）与8个县（枣强县、武邑县、武强县、饶阳县、安平县、故城县、景县、阜城县）。

衡水市地处河北冲积平原，是中国华北平原冬小麦的主产区之一。根据农气站物候资料，衡水地区冬小麦的播种时间一般约为10月中上旬，收获时间一般为次年6月初。衡水市一般采用灌溉式方式种植小麦，水肥条件充足，受水分胁迫或养分胁迫等因素的影响较小。

1.2 数据获取与预处理

1.2.1 地面实测数据

LAI地面实测数据利用LAI2000仪器测量得到，实测数据采样点的分布如图1所示。采样点共有22个，每个县各分布2个，编号如图1所示。在每个采样点附近随机选取5个采样位置并记录经纬度，每个位置进行5次LAI的测量，取平均值作为对应位置的LAI真值。

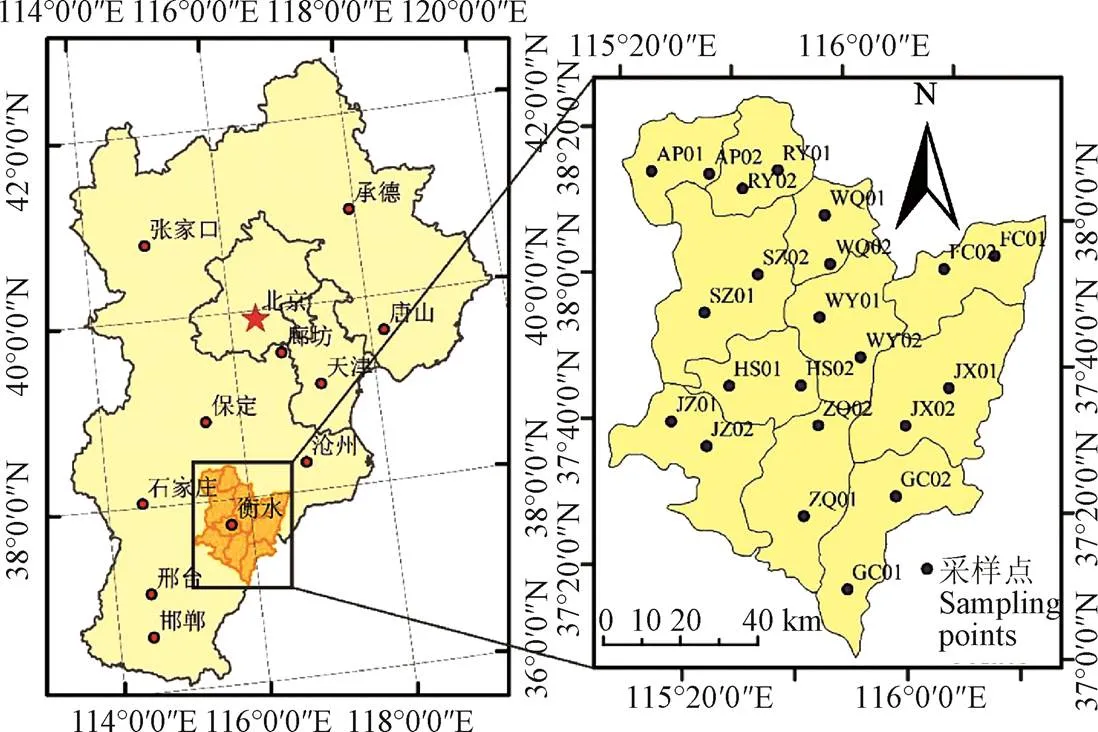
图1 研究区域与采样点分布

Fig.1 Studyareaandsamplingpoints distribution

在小麦的整个生育期内，共进行了2次LAI的实地测量，测量日期分别为2017-03-29—2017-04-01以及2017-05-04—2017-05-06，分别位于冬小麦生长发育的拔节期与抽穗—灌浆期。这两个生育期在冬小麦的生长过程中具有重要的意义，并且两个时期的生长状况不同，LAI相差较大，因此利用它们来对LAI的模拟进行同化修正可以有效的提升模拟精度。

两次地面测量共得到了110组实测的LAI值。主要用于：建立Sentinel-2卫星数据的LAI经验反演模型；SCE优化算法中的LAI真值输入；验证同化之后WOFOST模型输出的LAI精度。

1.2.2 气象站数据

为进行WOFOST模型的标定，本文选择位于衡水市地区的国家气象站——南宫气象站（台站编号54705，位于115.38°E，37.22°N）提供的2016年9月－2017年7月的中国地面气候资料日值数据（http://data.cma.cn）作为气象数据驱动WOFOST模型。在潜在生长水平模式下，WOFOST模型需要输入的驱动数据有日最高气温、日最低气温与日照时数，其余的如降水、肥力等数据则采用潜在水平下模型的默认数据。

为得到整个衡水地区每个像元内的LAI模拟曲线，本文选取了21个河北省内的国家气象台站（张北、蔚县、石家庄、邢台、丰宁、围场、张家口、怀来、承德、遵化、青龙、秦皇岛、霸州、唐山、唐海、乐亭、保定、饶阳、泊头、黄骅、南宫）的气象数据进行插值，并提取出衡水市内每个像元上的天气数据作为WOFOST模型的驱动数据。

1.2.3 Sentinel-2数据

Sentinel-2卫星数据在可见光、近红外、短波红外波长范围内共提供13个波段。本文选择空间分辨率为10 m的红光波段与近红外波段反射率数据，与两次地面测量相对应，所选择的Sentinel-2遥感影像的过境日期为2017-03-29与2017-05-04。这2景数据与地面实测数据一起构建LAI反演的经验模型，从而反演出衡水地区的LAI，为后续像元尺度的同化修正提供真值。

2 试验方法

本文的试验流程可概括如下：首先利用单点的气象数据驱动潜在水平下的WOFOST模型，结合EFAST算法得到影响模型运行最敏感的5个参数；再利用对应的单点实测LAI数据结合SCE算法对这几个敏感参数进行优化标定；接着将标定后的参数运用于整个衡水地区的每个像元，利用插值得到的每个像元的气象数据作为驱动，并将Sentinel-2反演得到的LAI数据作为真值对模型的模拟进行同化修正，最终得到每个像元的生长模拟结果，技术路线图如图2所示。

2.1 基于Sentinel-2的LAI反演

传统的基于NDVI模型反演的LAI在浓密植被覆盖地区往往出现饱和情况，为解决这一问题，Sun等[18]提出了反转差值植被指数（inverted difference vegetation index，IDVI）用于高植被覆盖地区的LAI反演。

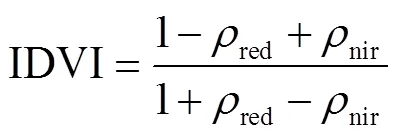
式中red和nir分别为红光和近红外波段的地表反射率。IDVI在浓密植被地区与LAI有较好的线性关系，而在植被稀疏地区的相关性较差。

为准确反演出研究区LAI，本文基于NDVI与IDVI构建统计回归模型，以解决2种指数各自在高植被覆盖区和低植被覆盖区的不足。

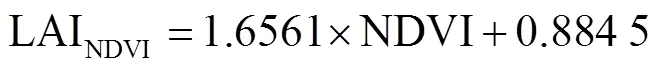
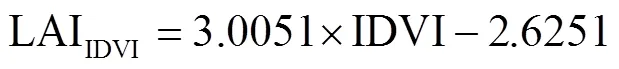
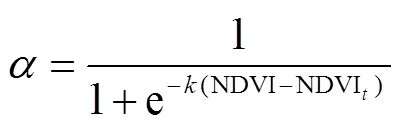
式中是Logistic形式的动态比例因子，NDVI为NDVI达到饱和时的阈值，为Logistic方程中的幅度系数。NDVI和在研究区域应用之前应当根据先验知识进行更新和调整。在本文中的具体表达式为

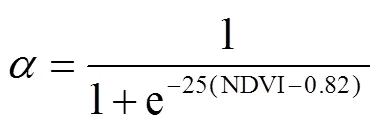
本文所使用的数据以及LAI的反演过程与Sun等[18]一致，通过文献[18]可知，利用IDVI反演得到的LAI的为0.91，RMSE为0.81.

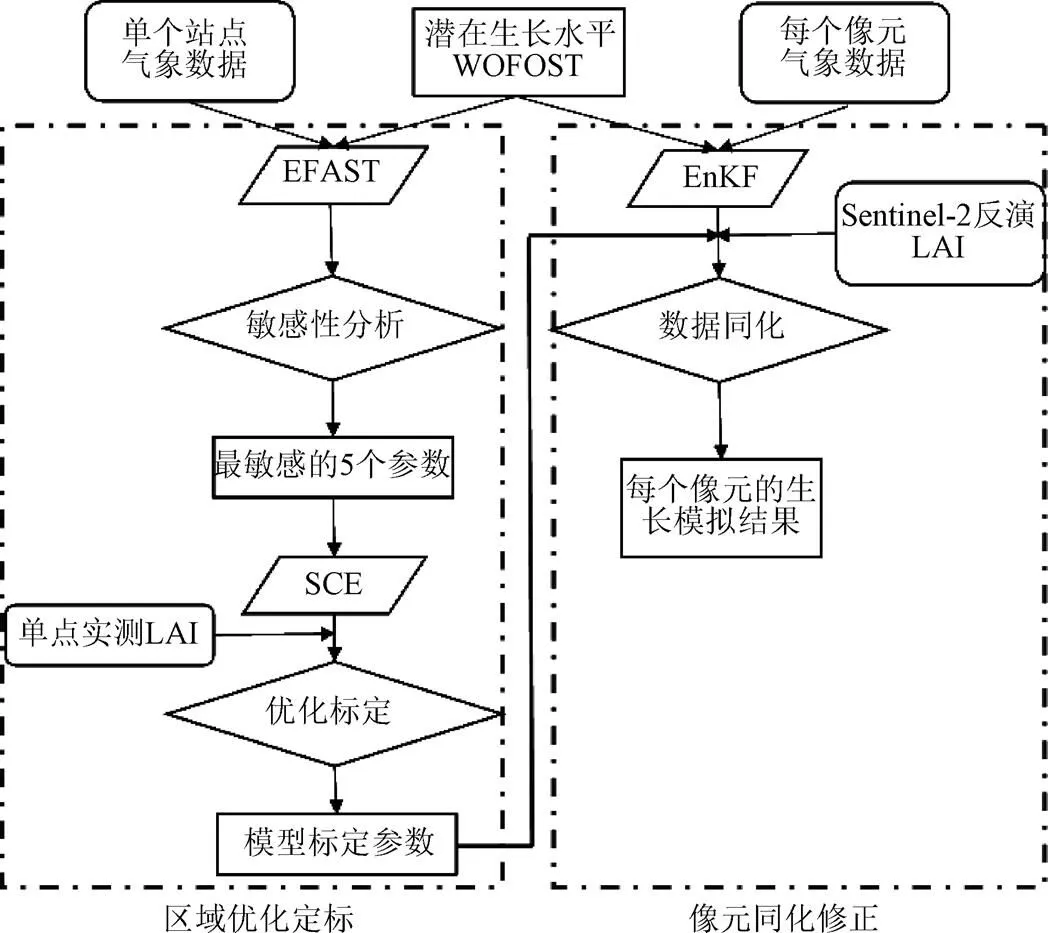
图2 技术路线图

2.2 EFAST

EFAST是一种基于方差理论的定量全局敏感性分析方法，对样本要求低，计算高效[13]，适用于WOFOST这种参数众多且关系复杂的模型的敏感性分析。其算法的基本思想是分解模型参数对模型模拟结果的方差，把参数敏感性分为2种类型：各参数对结果的影响以及参数之间耦合对模型结果的影响。其中单个参数独立作用是用主敏感度（main effect）衡量，而参数相互作用（interaction）则用总敏感度（total effect）和主敏感度之差来衡量。

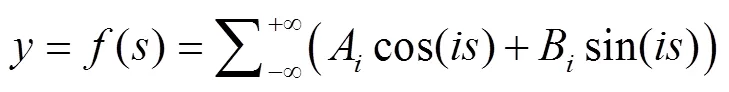
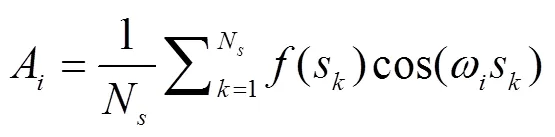
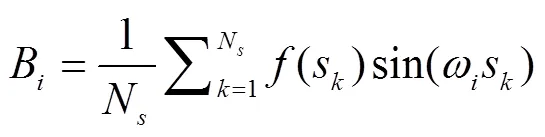
模型的总方差分解为

式中为V参数x输入变化单独引起的模型方差，V为参数x通过参数x作用贡献的耦合方差，V为参数x通过参数x、x作用贡献的耦合方差，依此类推。

通过归一化处理参数x的主敏感度S定义为

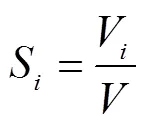
参数x的总敏感度为

式中−i为与参数x无关的所有其他参数方差之和（即去掉式（11）中所有含下标的方差项）。

2.3 SCE

SCE算法是段青云博士于1992年在Arizona大学水文与水资源系作研究时提出的全局优化算法，最初应用于水文模型的优化中[16]。它可以解决MCMC算法依赖于初值而难以收敛的问题，并且可以避免优化过程中陷入局部极值区而无法收敛于全局最优值。该算法继承了下山单纯形（downhill simplex）方法、控制随机搜索（controlled random search）方法，竞争演化（competitive evolution）方法和洗牌（shuffling）算法等算法的特色，通过最小化代价函数，迅速找到全局最优解。

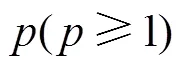
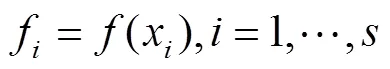
3）样本点排序：把个样本点函数值（x,f）按升序排列，排序后仍记为(x,f)，=1,…,。其中,将排序后的点存在中；

4）划分复合形群体：将划分为个复合形1,···,A，每个复合形含有个点。

5）复合形演化：通过CCE方法[16]，对每个复合形分别演化。

6）复合形混合：把演化后的每个复合形的所有点组合，生成新的点集，再次按函数值f升序排列；

7）收敛判断：如果满足收敛条件则停止，否则返回步骤（4）。

其中的CCE算法是下山单纯形方法的拓展，通过竞争机制决定复杂形参与演化的是哪些点。该算法根据每个点的目标函数值，采用特定方法来确定每个点被选择的概率，从而保证目标函数值较高的点，参加演化的概率大于目标函数值较低的点，同时目标函数最低的点也有参加演化的机会。

2.4 EnKF

EnKF由Evensen提出，其核心思想是利用集合成员的统计来得到误差协方阵，以避免复杂算子的计算[15]。EnKF在处理各种数据不确定性时比较灵活，算法易于实现和操作，因此被广泛应用于地表数据同化研究中。

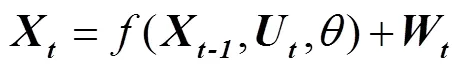
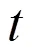
同化的过程分为预测和分析2个部分。

首先通过模型的运行得到LAI的一步预测值：

但一步预测值只是通过模型向前运行得到的，要得到时刻LAI的估计值，还需要将该时刻的卫星反演值同化进去

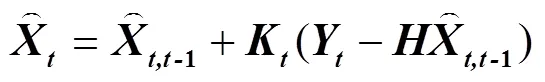
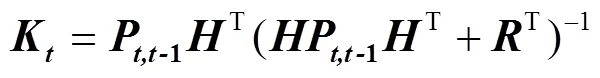
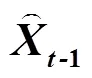
根据以上处理，可以得到

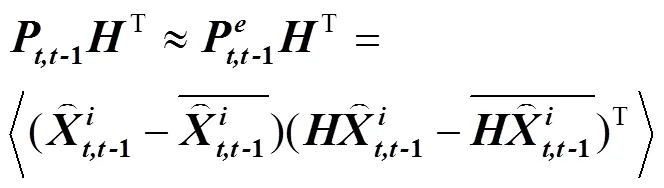
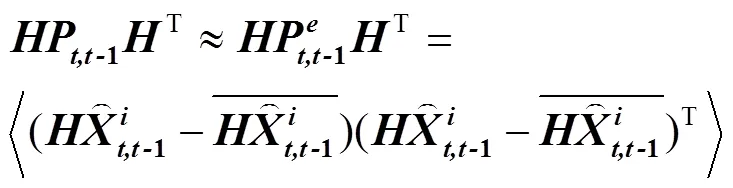
由此可以方便地计算出滤波增益的值，进而得到时刻LAI的估计值。同理可以得到时刻LAI估计值的误差P。

3 结果与分析

3.1 敏感性分析结果

WOFOST模型可输出作物全生育期逐日的叶面积指数、地上总干物质量以及最终产量，对于不同的目标输出，模型输入参数的影响程度也不同（例如可以模拟出最优LAI的模型不一定能够模拟出最优的最终产量）。由于本文同化的参数为LAI，因此选取作物生育期最大叶面积指数（LAImax）作为分析对象，结合南宫气象站提供的气象数据作为驱动，在单点采用EFAST算法对WOFOST模型的14项重要输入参数进行敏感性分析。参数的取值范围与最终分析结果如表1所示。

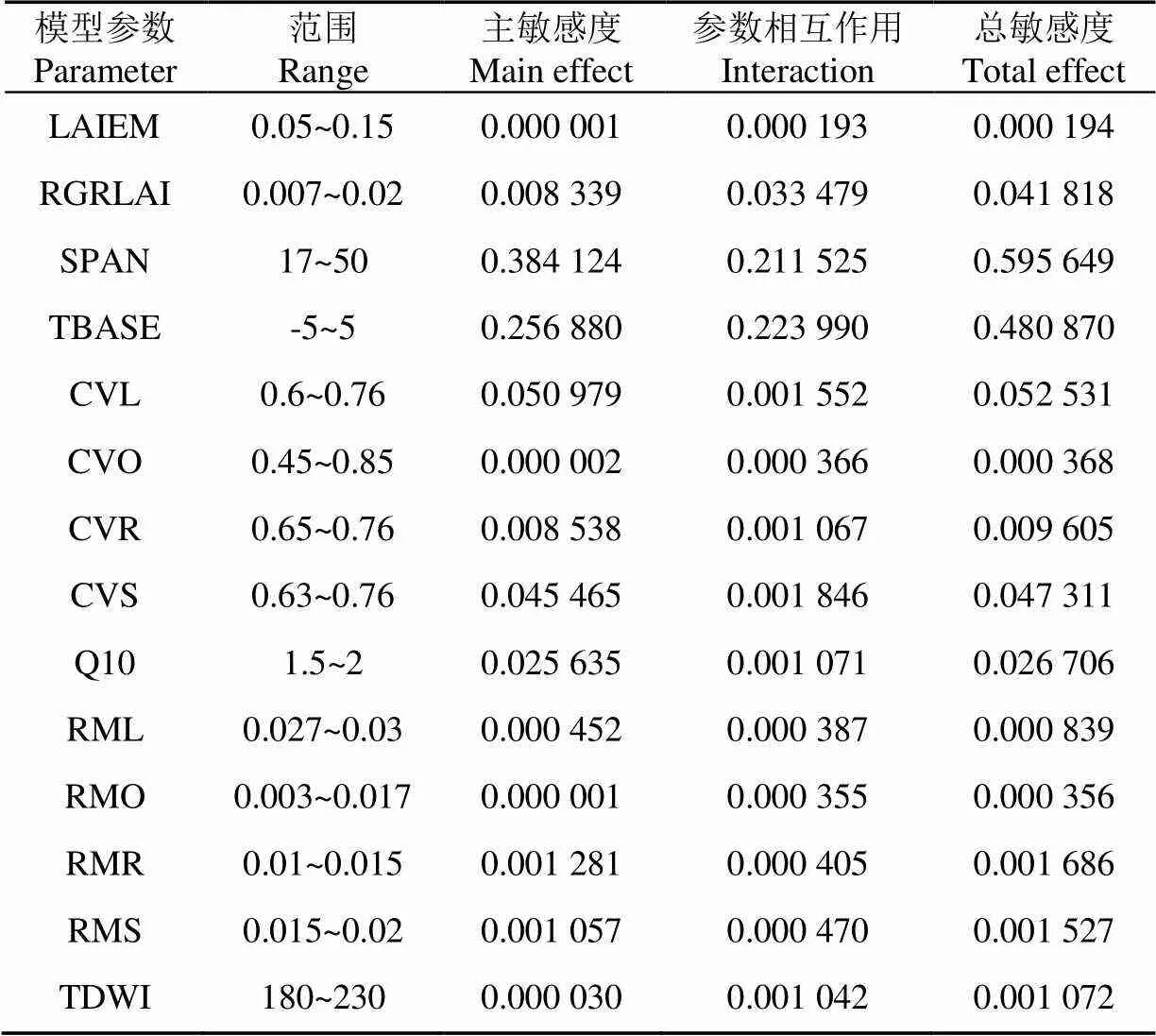
表1 WOFOST模型参数对冬小麦生育期最大叶面积指数（LAImax）的影响

从表1中可以看出，对作物生育期最大叶面积指数（LAImax）总敏感度最大的5个模型输入参数依次为：SPAN、TBASE、CVL、CVS、RGRLAI。其中SPAN、TBASE 和RGRLAI与作物叶片的存活时间相关，CVS、CVL则与呼吸作用积累同化物以及同化物转化成干物质密切相关。

3.2 SCE优化算法结果

对于上述的5个总敏感度最高的参数，进一步在该点采用SCE算法对模型进行优化标定，对于其他参数，采用相关文献中的推荐值[11-12,19-28]。最终WOFOST模型输入参数如表2所示。

3.3 冬小麦全生育期LAI反演结果与对比验证

3.3.1 SCE优化前后LAI结果对比

为展示SCE优化方法的效果，分别利用SCE算法优化前后的WOFOST模型模拟采样点HS01所在区域内的冬小麦生长状况，如图3所示。

从图3中可以看出，优化后的时序LAI曲线更加接近所给的2个日期的LAI真值，也即通过SCE优化后的WOFOST模型更适合对衡水地区冬小麦的生长状况进行模拟。

表2 SCE算法优化WOFOST模型标定后部分参数取值

注：“/”左侧为优化前的参数值，“/”右侧为优化后的参数值。

Note: The values before optimization are on the left hand of ‘/’ and that after optimization are on the right hand of ‘/’.

图3 HS01采样点在WOFOST模型经SCE优化前后的冬小麦时序LAI曲线

3.3.2 EnKF同化结果与验证

利用标定后的WOFOST模型模拟衡水地区每个像元内的冬小麦生长情况，并结合Sentinel-2反演所得到的LAI值进行数据同化，并分别从时间和空间上对所得到的结果进行展示。

时间上选取采样点HS01所得到的时序LAI曲线进行绘制，如图4所示；空间上选取2017-03-30与2017-05-05这2个日期整个衡水市的LAI分布情况进行绘制，如图5所示。

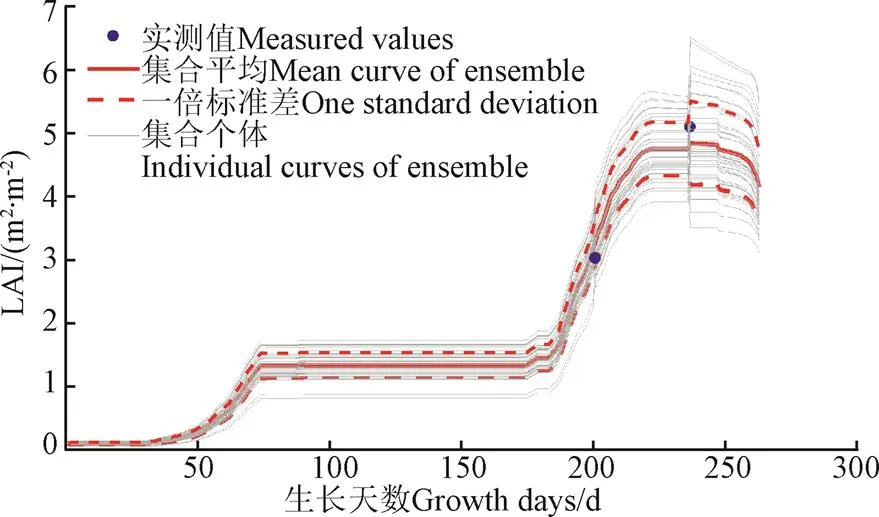
图4 WOFOST模型经EnKF同化后在HS01采样点的冬小麦全生育期时序LAI曲线

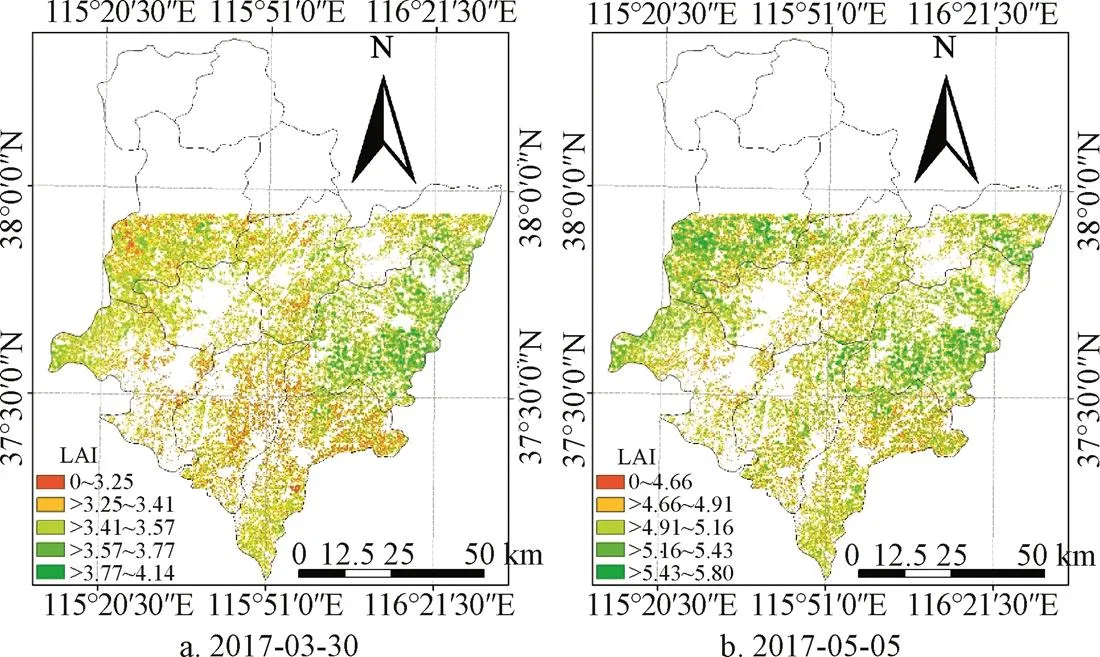
图5 SCE定标与EnKF同化后模型模拟的特定日期的衡水地区LAI分布

可以发现，在圆点处，原本光滑的LAI曲线会出现向点靠近的凹陷与凸起，这种现象说明了WOFOST模型的模拟与真实值有一定的偏差，而数据同化可以通过在某些时刻加入观测值，将模拟曲线拉回到与真实值更加接近的水平，进而提高模型的模拟精度。

图5中，模拟结果在衡水市的北部有一片空白区域，这是因为所选择的两景Sentinel-2影像没有覆盖到这些地区，因此依赖于观测值的数据同化无法进行。为了直观的展示出小麦种植区的LAI分布，在遥感影像覆盖区域，本文利用2017衡水地区冬小麦的种植面积[29]将模拟结果进行掩膜提取。

为验证本文研究方法所模拟得到的衡水地区LAI的精度，将图5中2个日期的LAI模拟值分布图中与采样点相对应像元的值分别提取出来，并与地面实测数据进行对比验证，如图6所示。

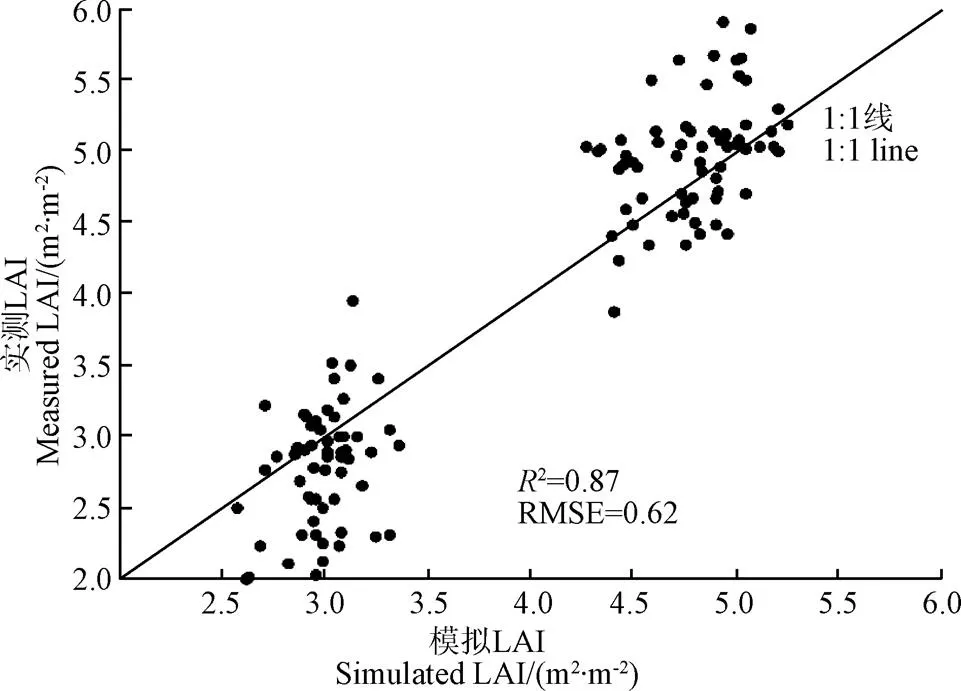
图6 WOFOST模拟所得LAI与实测数据比较

从图6中可以看出，同化得到的LAI与实测LAI的散点基本分布在1:1线附近，当LAI值较低时，同化得到的LAI存在高估现象，当LAI值较高时，同化得到的LAI存在低估现象。同化结果与实测数据存在较好的相关性，2为0.87，RMSE为0.62，同化结果与实测数据之间的差异较小。而只采取查阅文献与经验标定的方法对参数进行校准的WOFOST模型模拟得到的LAI与真实值之间的2在0.70～0.83之间，RMSE在0.89～1.36之间[11]。因此，利用本文提出的方法所模拟的LAI的2有所提高，RMSE有所降低，同化效果较好，所得LAI的精度较高，可以有效表征冬小麦的长势情况。

4 讨 论

本文的目的是使用WOFOST模型模拟衡水地区冬小麦的生长状况，从而得到全生育期的时序LAI曲线。在模型的标定上，本文利用EFAST模型获取最敏感的几个参数，既避免了凭经验选取参数的主观性，又减小了后续优化过程的计算量；同时，本文利用的SCE算法可以使待优化的参数快速收敛到全局最优值，解决了MCMC算法依赖于初值选取的问题。在模型的区域尺度应用方面，本文通过EnKF结合遥感数据反演LAI对标定后的模型进行数据同化，使得模型在每个像元上模拟得到的LAI准确度更高。总的来说，本文所提出的“区域优化标定，像元同化修正”的研究方法对WOFOST模型在中国区域尺度上的应用具有一定的参考意义。

在结果验证方面，采取时序的LAI实测数据或已有的时序LAI产品与模型模拟所得到的LAI曲线进行对比更能反应本文研究工作的意义。但时序LAI的实测耗时耗力，现有的MODIS-LAI产品分辨率过大，且精度又达不到应用需求[26]，因此本文只选择了小麦生长过程中两个时间点的实测LAI数据在空间尺度上对WOFOST模型的模拟结果进行了验证。从验证的结果可以看出，模型在某些采样点的模拟值并不够准确，但WOFOST模型的目的在于获取小麦生长过程中LAI变化趋势，其单点模拟LAI的准确度并不能达到遥感反演结果的水平，与其他WOFOST模型的应用方法比较，本文的研究方法所模拟得到的LAI精度已经达到了较高的水准。同时，这些不准确的点也反映了在区域内每个像元上仅仅使用标定的WOFOST模型有很大偏差，在定标之后进行“像元同化修正”是必要的。

5 结 论

本文通过潜在生长水平下的WOFOST模型对衡水地区冬小麦的LAI进行模拟分析，提出了一种“区域优化标定，像元同化修正”的研究方法。结果表明，利用EFAST算法对模型的参数敏感性进行分析，再结合地面实测数据，利用SCE算法对最敏感的几个参数进行优化后的模型更适用于该地区。为准确地模拟区域尺度上的冬小麦时序LAI，本文结合了Sentinel-2卫星数据反演得到的LAI，利用EnKF算法对优化后的WOFOST模型进行数据同化，所得到的LAI的2为0.87，RMSE为0.62，均达到较好的水平，模拟精度较高。本文的意义在于提供了从模型标定到具体模拟整个过程中各个环节的思路与方法，使得对WOFOST模型的应用不再仅仅依靠经验，这有利于WOFOST模型在中国区域尺度上的应用。

[1] Fan W J, Gai Y Y, Xu X R, et al. The spatial scaling effect of the discrete-canopy effective leaf area index retrieved by remote sensing[J]. Science China Earth Sciences, 2013, 56(9): 1548－1554.

[2] Liu Yang, Liu Ronggao, Chen Jingming, et al. Current status and perspectives of leaf area index retrieval from optical remote sensing data[J]. Journal of Geo-Information Science, 2013, 15(5):734－743.

[3] 刘良云．高光谱遥感在精准农业中的应用研究[R]．中国科学院遥感应用研究所博士后出站报告，2002．

[4] Tillack A, Clasen A, Kleinschmit B, et al. Estimation of the seasonal leaf area index in an alluvial forest using high-resolution satellite-based vegetation indices[J]. Remote Sensing of Environment, 2014, 141(141): 52－63.

[5] Rasmus Houborg, Henrik Soegaard. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data[J]. Remote Sensing of Environment, 2007, 106(1): 39－58.

[6] Baret F, Jacquemoud S, Guyot G, et al. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands[J]. Remote Sensing of Environment, 1992, 41(2/3): 133－142.

[7] Diepen C A, Wolf J, Keulen H, et al. WOFOST: A simulation model of crop production[J]. Soil Use & Management, 2010, 5(1): 16－24.

[8] Rabier F, Thépaut J N, Courtier P. Extended assimilation and forecast experiments with a four‐dimensional variational assimilation system[J]. Quarterly Journal of the Royal Meteorological Society, 1998, 124(550): 1861－1887.

[9] Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering Transactions, 1960, 82: 35－45.

[10] 张素青，张建涛，李继蕊，等. WOFOST模型在河南省夏玉米主产区的校准与验证[J]. 河南农业科学，2014，43(8)：152－156.

Zhang Suqing, Zhang Jiantao, Li Jirui, et al. Calibration and validation of WOFOST in main maize-producing regions in Henan[J]. Journal of Henan Agricultural Sciences, 2014, 43(8): 152－156. (in Chinese with English abstract)

[11] 黄健熙，贾世灵，马鸿元，等. 基于WOFOST模型的中国主产区冬小麦生长过程动态模拟[J]. 农业工程学报，2017，33(10)：222－228.

Huang Jianxi, Jia Shiling, Ma Hongyuan, et al. Dynamic simulation of growth process of winter wheat in main production areas of China based on WOFOST model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(10): 222－228. (in Chinese with English abstract)

[12] 何亮，侯英雨，赵刚，等. 基于全局敏感性分析和贝叶斯方法的WOFOST作物模型参数优化[J]. 农业工程学报，2016，32(2)：169－179.

He Liang, Hou Yingyu, Zhao Gang, et al. Parameters optimization of WOFOST model by integration of global sensitivity analysis and Bayesian calibration method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 169－179. (in Chinese with English abstract)

[13] Mcculloch A. Sensitivity analysis in practice: A guide to assessing scientific models[J]. Publications of the American Statistical Association, 2005, 101(473): 398－399.

[14] 范丽颖. 基于集合Kalman滤波的作物生长模型与遥感数据的同化研究[D]. 北京：中国农业科学院，2012.

[15] Evensen G. The ensemble Kalman filter: Theoretical formulation and practical implementation[J]. Ocean Dynamics, 2003, 53(4): 343－367.

[16] Duan Q Y, Gupta V K, Sorooshian S. Shuffled complex evolution approach for effective and efficient global minimization[J]. Journal of Optimization Theory and Applications, 1993, 76(3): 501－521.

[17] Richter K, Atzberger C, Vuolo F, et al. Evaluation of Sentinel-2 spectral sampling for radiative transfer model based LAI estimation of wheat, sugar beet, and maize[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2011, 4(2): 458－464.

[18] Sun Y, Ren H, Zhang T, et al. Crop leaf area index retrieval based on inverted difference vegetation index and NDVI[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(11): 1662－1666.

[19] Huang J, Sedano F, Huang Y, et al. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation[J]. Agricultural and Forest Meteorology, 2016, 216: 188－202.

[20] Huang J, Tian L, Liang S, et al. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model[J]. Agricultural and Forest Meteorology, 2015, 204: 106－121.

[21] Ma G, Huang J, Wu W, et al. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield[J]. Mathematical & Computer Modelling, 2013, 58(3/4): 634－643.

[22] Ma Hongyuan, Huang Jianxi, Zhu Dehai, et al. Estimating regional winter wheat yield by assimilation of time series of HJ-1 CCD NDVI into WOFOST-ACRM model with Ensemble Kalman filter[J]. Mathematical & Computer Modelling, 2013, 58(3/4): 759－770.

[23] Huang Jianxi, Ma Hongyuan, Su Wei, et al. Jointly assimilating MODIS LAI and ET products into the SWAP model to estimate winter wheat yield[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4060－4071.

[24] Tian Liyan, Li Zhongxia, Huang Jianxi, et al. Comparison of two optimization algorithms for estimating regional winter wheat yield by integrating MODIS leaf area index and world food studies model[J]. Sensor Letters, 2013, 11(6/7): 1261－1268.

[25] 黄健熙，马鸿元，田丽燕，等. 基于时间序列LAI和ET同化的冬小麦遥感估产方法比较[J]. 农业工程学报，2015，31(4)：197－203.

Huang Jianxi, Ma Hongyuan, Tian Liyan, et al. Comparison of remote sensing yield estimation methods for winter wheat based on assimilating time-sequence LAI and ET[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(4): 197－203.(in Chinese with English abstract)

[26] 黄健熙，武思杰，刘兴权，等. 基于遥感信息与作物模型集合卡尔曼滤波同化的区域冬小麦产量预测[J]. 农业工程学报，2012，28(4)：142－148.

Huang Jianxi, Wu Sijie, Liu Xingquan, et al. Regional winter wheat yield forecasting based on assimilation of remote sensing data and crop growth model with Ensemble Kalman method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(4): 142－148. (in Chinese with English abstract)

[27] 邱美娟，宋迎波，王建林，等. 山东省冬小麦产量动态集成预报方法[J]. 应用气象学报，2016，27(2)：191－200.

Qiu Meijuan, Song Yingbo, Wang Jianlin, et al. Integrated technology of yield dynamic prediction of winter wheat in Shandong province[J]. Journal of applied meteorological science, 2016, 27(2): 191－200.(in Chinese with English abstract)

[28] Wu D, Yu Q, Lu C, et al. Quantifying production potentials of winter wheat in the North China Plain[J]. European Journal of Agronomy, 2006, 24(3): 226－235.

[29] Sui J, Qin Q, Ren H, et al. Winter wheat production estimation based on environmental stress factors from satellite observations[J]. Remote Sensing, 2018, 10(6): 962.

Time-series LAI simulation of winter wheat based on WOFOST model calibrated by SCE and assimilated by EnKF

Xu Wei, Qin Qiming※, Zhang Tianyuan, Long Zehao

(100871)

WOFOST (world food studies) model can be used to simulate time-series LAI (leaf area index), the organs’ biomass, and the yields of winter wheat. Therefore, it is meaningful for the growth monitoring and production prediction of winter wheat. So far, the calibration of WOFOST usually relies on researches’ experience, which brings many problems while using the model in a specific area. As a result, we focus on the calibration problem and try to improve the accuracy of the simulated results in this paper. The potential production WOFOST was analyzed and LAI was chosen as the measure index because it was easy to obtain. In this study, we selected Hengshui as the study area, and two field experiments were carried out in this area during two different periods. One period was from 2017-03-29 to 2017-04-01 and the other was from 2017-05-04 to 2017-05-06. It was divided into 11 sampling areas and 5 sampling points in every area were obtained to measure the LAI, so we got approximately 110 measured data totally. A method called ‘Calibrating in area by optimization and correcting at pixel by assimilation’ was presented in this paper. Firstly, calibrating WOFOST model in local area: The weather data including sunshine duration data and the maximum and minimum air temperature data every day were used to run the WOFOST model. The data were from Nangong National Weather Station and can be downloaded in National Meteorological Information Center. Then the sensitivity of model parameters can be analyzed with EFAST (extend fourier amplitude sensitivity test) and the 5 most sensitive parameters were selected to optimize the model. It was worthwhile to note that there were different indices to evaluate the sensitivity of every parameter, such as main effect, interaction, and total effect, and the total effect was considered as the most important index in this study. As for the optimization, the SCE (shuffled complex evolution) algorithm was used which could find the global optimal solution fastly. It can solve the initial value dependence problem and local convergence problem which might exist in other optimization algorithms such as MCMC (Markov Chain Monte Carlo). In order to proof that the optimization was valid, the time-series LAI curves simulated were compared by WOFOST before and after optimization with SCE with measured values. It turned out the model after optimization was much more appropriate to simulate the growth of winter wheat in study area. Secondly, assimilating the model in every pixel in the study area: We interpolated weather data from 21 National Weather Stations in Hebei Province in order to run WOFOST in every pixel. Based on this, EnKF (Ensemble Kalman Filter) was used to assimilate LAI in every pixel with the remote sensing data from Sentinel-2. As a result, we could get the time-series LAI curve at every pixel. The LAI curve at point HS01 was illustrated and it was obvious that assimilation made a difference in the simulation. Additionally, the simulated LAI distribution maps were illustrated in Hengshui at date of 2017-03-30 and 2017-05-05. And the simulated LAI values of the pixels according to the sampling points were extracted. By comparing the simulated LAI with measured LAI, we found that2was increased from 0.70-0.83 to 0.87 and RMSE was decreased from 0.89-1.36 to 0.62. Therefore, the method proposed in this study solved the calibration problem and improved the accuracy of time-series LAI simulated compared with other studies. In addition, we provided specific theories and methods in every stage from calibration to application. It contributed to the application of WOFOST in our country.

models; remote sensing; winter wheat; time-series LAI; WOFOST; SCE

2018-08-10

2019-06-12

国家高分重大专项“GF-7卫星高精度农作物信息提取技术”（11-Y20A16-9001-17/18）；国家重点研发计划课题“作物生长与生产力卫星遥感监测预测”（2016YFD0300603）

许 伟，安徽芜湖人，博士生，主要研究方向为农业定量遥感。Email：xuwei1995@pku.edu.cn

秦其明，江苏徐州人，教授，博士，博士生导师，主要研究方向为定量遥感与地理信息系统。Email：qmqin@pku.edu.cn

10.11975/j.issn.1002-6819.2019.14.021

S127; S512.1; TP79

A

1002-6819(2019)-14-0166-08

许 伟，秦其明，张添源，龙泽昊. SCE标定结合EnKF同化遥感和WOFOST模型模拟冬小麦时序LAI[J]. 农业工程学报，2019，35(14)：166－173. doi：10.11975/j.issn.1002-6819.2019.14.021 http://www.tcsae.org

Xu Wei, Qin Qiming, Zhang Tianyuan, Long Zehao. Time-series LAI simulation of winter wheat based on WOFOST model calibrated by SCE and assimilated by EnKF[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 166－173. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.14.021 http://www.tcsae.org