混合偏最小二乘回归和粒子群优化直接进给轴加速度饱和性能的优化方法
林献坤 张立明
1.上海理工大学机械工程学院,上海,2000932.上海理工大学苏州精密制造技术研究院,苏州,320507
0 引言
直线电机是一种将电能直接转换成直线运动机械能,不需要中间转换机构的传动装置,它具有定位精度高、传动效率高、推力大和加速度大等优点,已广泛应用于精密数控机床加工中[1]。在高加速进给的条件下,由直线电机驱动的进给轴能够在短行程内产生较高的进给速度,提高了加工效率;高切削速度使得切削过程中的发热量更小,降低能耗,又可使工件轮廓误差更小,提高加工精度[2]。加速度饱和性能评价指标是指在一定行程范围和加速度最高值限定范围内使进给过程速度的时间积分值(即驱动过程最高加速度绝对值)持续的时间,该性能参数也是衡量是否能保持高速度进给过程的重要指标。由于直线电机特殊的机械结构、端部效应、推力波纹以及摩擦阻力等诸多因素的存在,影响到进给驱动过程的加速度,加速度饱和性能对于提高加工效率和加工质量具有重要意义[3-4]。
直接进给轴加速度的抗扰动能力是其驱动性能的重要因素,并且驱动性能受到电机推力波动与包括摩擦力在内的扰动力等诸多因素的影响,国内外专家学者对此做了较多的研究。TAVANA等[5]提出了一种基于麦克斯韦方程组的分析方法,利用遗传算法对影响电机推力的参数进行了优化;HAN等[6]通过加入加速度反馈环节,分析了伺服系统的抗扰动性和加速度闭环的稳定性;GUO等[7]提出具有反馈输入环节的扰动观测器模型,对负载扰动进行了深入分析;赖国庭等[8]通过加速度的前馈控制策略,对永磁伺服电机的驱动性能进行了研究;ITAGAKI等[9]通过构建非线性摩擦迟滞特性的模型,采用线性虚拟摩擦的方法,对进给轴摩擦的补偿进行了研究;向红标等[10]提出一种基于LuGre模型的自适应摩擦补偿方法,对伺服系统的摩擦干扰进行了研究。上述对直接进给轴驱动性能的研究,都是基于建立精确的电机模型,在电机模型的基础上通过设计控制器或观测器等开展的。但在实际工程中,建立精确的电机模型往往难以实现;影响进给轴驱动性能的非线性因素众多又相互作用,对一些扰动的实时观测较为困难,要提高直接进给轴驱动性能有一定的局限性。
由于对进给轴各种扰动因素的控制,都与伺服参数的配置环节有关,因此,将扰动看作系统内在固有特性,利用试验方法获得系统的输入与输出,建立数学模型,进行伺服参数优化的方法,已成为提高驱动性能的热点研究方向[11]。LEE等[12]提出用神经网络、支持向量机等方法提高直接进给轴的驱动性能。陈东宁等[13]提出一种细菌群觅食优化算法,对伺服系统的控制参数进行了深入研究。俞亚新等[14]提出一种模糊变系数PID控制器,利用模糊控制原理在线调整PID控制器的比例、积分及微分增益。林献坤等[15]通过分析数控系统中应用伯德图优化伺服参数存在的问题,给出了一种基于动刚度评价的直接进给轴伺服参数优化方法。
本文以自构建的直线电机驱动进给轴为研究对象,通过分析进给轴加速度饱和性能的影响因素,对其加速度饱和性能的优化方法进行了研究。
1 加速度饱和性能的影响因素分析
永磁直线伺服电机的动力学方程:
(1)
式中,Fe为电机推力;m为动子及负载的总质量;x为运动位移;t为运动时间;Fc为摩擦力;ΔF为非线性因素摄动引起的扰动力。
由式(1)可知,直接进给轴加速度与电机推力有着直接的关系。永磁同步直线电机在d-q坐标轴下的电压方程:
(2)
式中,ud和uq为动子端d轴和q轴的电压分量;Rs为永磁同步直线电机动子绕组的电阻值;ψd和ψq为d、q轴动子感链;ω为直线电机平移速度折算成的旋转电机角速度。
磁链方程:
(3)
式中,Ld和Lq分别为电机d轴和q轴电感;id和iq分别为d轴和q轴动子电流;ψf为定子永磁体产生的励磁磁链。
由此可得电机推力:
(4)
当永磁直线电机进行矢量控制时,即要求动子电流矢量与定子永磁体磁场在空间正交。如果id=0,电机推力Fe与iq成正比,即
(5)
式中,Kf为电机推力系数。
所以,式(1)可转换为
(6)
直线电机伺服控制系统是由3层闭环结构组成,从内而外分别为电流环、速度环和位置环。电流环用来抑制电流干扰信号,提高系统的快速性和稳定性,且电流环给定i是速度环的输出信号;速度环采用PI调节器,用来消除力矩扰动和速度波动,提高系统抗负载扰动能力,且速度环给定u是位置环的输出信号;位置环采用P调节器,用来提高系统静态精度和动态跟踪能力,保证伺服系统的精度和稳定,位置环给定是运动指令x*。结合式(6)可得图1所示的直线电机伺服加速度控制框图。图中,KPs为位置环比例增益;KPv为速度环比例增益;KIv为速度环积分增益;KPi为电流环比例增益;KIi为电流环积分增益;Ke为反电势常数。
从图1可以看出,在特定系统的前提下,电机推力系数Kf、动子及负载的总质量m以及控制环节1/s皆是固定不变的,电流环参数在直线电机和功率模块选定之后通常保持不变,在研究中,不对

图1 直线电机伺服驱动控制原理图Fig.1 Control block diagram of linear motor servo acceleration
该环节进行优化,而伺服参数Ks、KPv、KIv是可以调节变动的,与加速度之间存在着紧密的联系。
2 加速度饱和性能建模
2.1 偏最小二乘回归建模的应用
偏最小二乘回归方法是建立在X(自变量)与Y(因变量)矩阵基础上的双线性模型,可以看作是由外部关系(即独立的X块和Y块)和内部关系(即两块间的关系)构成。本文以伺服参数位置比例增益Ks、速度比例增益KPv以及速度积分KIv为自变量,运动时间t和速度最大超调量σ为因变量,通过分析自变量和因变量各自的潜变量,建立自变量与因变量的线性回归模型。
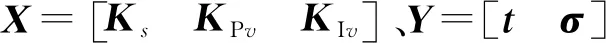
记E0为自变量集合X的标准化矩阵,有
(7)
i=1,2,…,nj=1,2,3

记F0为自变量集合Y的标准化矩阵,有
(8)
i=1,2,…,nj=1,2
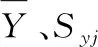
偏最小二乘回归分析建模时,先要从两组变量分别提取第一对成分为t1和u1,t1是自变量X的线性组合:t1=w11Ks+w12KPv+w13KIv,u1是因变量Y的线性组合:t1=v11t+v12σ,同时需满足以下要求:①t1和u1各自尽可能多地提取所在变量组的变异信息;②t1和u1的相关程度达到最大。综合起来,即要求第一对成分t1和u1的协方差Cov(t1,u1)最大:
(9)

(10)
式中,α1为自变量X的3×1阶回归系数向量;β1为因变量Y的1×1阶回归系数向量;E1和F1为回归方程的残差矩阵。
以残差阵E1和F1代替E0和F0重复以上步骤得到第二个主成分t2及相应的残差矩阵E2和F2,如此循环直到第r个主成分满足精度要求。最后可实现E0和F0在t1,t2,…,tr上的回归:
(11)

t=a11Ks+a12KPv+a13KIv
(12)
σ=a21Ks+a22KPv+a23KIv
(13)
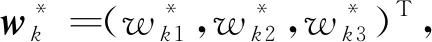
2.2 变量提取的收敛评判
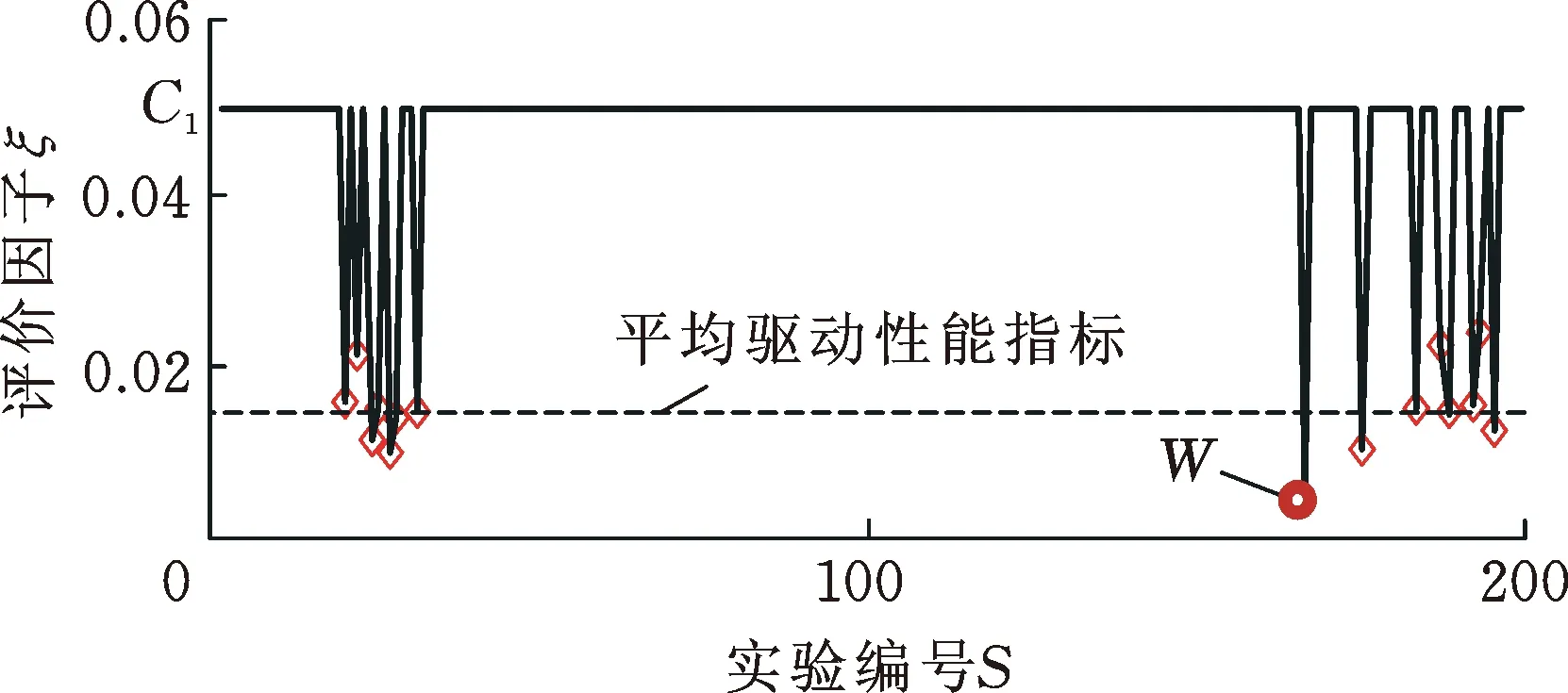
在应用偏最小二乘回归的方法对加速度饱和性能进行建模的过程中,并不需要选用全部的成分t1,t2,…,tr(r=rank(X))进行回归建模。事实上,如果后续的成分已经不能为解释F0提供更有意义的信息,采用过多的成分只会破坏对加速度饱和性能统计趋势的认识,引导错误的预测结论;仅用前l个成分t1,t2,…,tl(l (14) j=1,2 式中,P(h)是提取成分数为h时回归模型的拟合误差平方和;S(h-1)是提取成分数为h-1时因变量的变异平方和;yij是因变量原始数据;yij(h-1)是以全部样本点为基础,并取h-1个成分建模后第i个样本点的拟合值;y(i)j(h)是删除第i个样本点后,并取h个成分建模的第i个样本点的拟合值。 在高精密数控机床加工中,伺服控制系统不仅需要有快速的响应特性,还要有良好的稳态精度。其中,速度的超调量是影响系统稳态精度和跟踪性能的关键因素。过大的速度超调量,使得系统的振荡性能变差,影响了工件的加工精度、表面粗糙度以及机床的定位精度;长期的振荡抖动还会造成机械联接装置的磨损,进而损坏机床,严重时会酿成生产事故。因此,对于加速度饱和性能的优化,速度超调量的抑制是需要考虑的重要约束条件。 粒子群优化(particle swarm optimization,PSO)算法能够快速有效地解决工程中的可靠性优化问题,它不但具有全局寻优能力,而且通过调整参数也具备较强的局部寻优能力,能够不依赖于初值的选取和不用考虑目标函数是否可微,尤其在多维空间内非线性有约束的优化问题中取得了良好的效果。本文利用粒子群算法,以运动时间t关于伺服参数的数学模型为适应度函数,在速度最大超调量σ的约束下辨识优化参数。粒子群算法首先初始化得到一组随机解,以这组随机解为基础,通过迭代搜索最优解。由式(12)、式(13)中存在3个自变量(Ks,KPv,KIv)可知,本文通过粒子群算法优化的问题是在三维空间内搜索,即d=3。假设有m个粒子,粒子i位置可表示为Xi=(Xi1,Xi2,Xi3);粒子i的速度为vi=(vi1,vi2,vi3);每个粒子都有一个由优化目标函数(式(12))决定的适应值,粒子i个体经历过的最好位置为bpi=(pi1,pi2,pi3);种群经历过的最好位置为bgi=(g1,g2,g3)。粒子就是根据这两个极值来不断更新自己的速度和位置: (15) (16) 根据随机权重法,本文的惯性系数λ在搜索过程中按照下式变化: (17) 式中,N(0,1)表示服从标准正态分布的随机数;rand(0,1)表示在0到1之间产生的随机数。 本文对于加速度饱和性能优化方法的研究,包含加速度饱和性能的建模和优化参数的辨识两个部分,建模和计算流程如图2所示。 首先,在一定位移条件下,通过位移采集系统获取不同伺服参数时运动时间t和速度最大超调量σ的数据。将伺服参数序列(自变量)与运动时间t、速度最大超调量σ数据(因变量)建立统计样本库,应用偏最小二乘回归方法,通过提取潜变量和交叉有效性分析得到回归系数,构建运动时间t和速度最大超调量σ关于位置比例Ks、速度环比例增益KPv以及速度环积分增益KIv的数学模型。然后,以运动时间t关于伺服参数(Ks,KPv,KIv)的数学模型为适应度函数,设定速度最大超调量σ不大于5 mm/s为优化条件,通过粒子群优化算法进行优化参数的辨识。 图2 建模和计算流程图Fig.2 Flow chart of modeling and calculating 为了验证本文给出的直接进给轴加速度饱和性能优化方法的可行性,建立了图3所示的试验系统,该系统以有铁芯-无冷却的直接进给机构为试验平台,最大推力为5 000 N,最大速度可达1 000 mm/s,工作台行程为337 mm。应用GTS-400-PV运动控制卡和EDD-3020-T0S驱动器,构成该试验平台的伺服控制系统,应用MCV-500激光多普勒位移测量仪、IPC1-400高频数据采集卡组成位移采集系统。伺服控制系统、位移采集系统与安装有集成开发环境和位移采集软件的计算机,构成了完整的试验测试系统。 1.数据采集计算机 2.上位机 3.端子板 4.激光发射装置 5.激光反射标靶 6.欧姆龙EE-SX-67限位开关图3 试验平台布置Fig.3 Experimental platform layout 位移采集系统采用双通道双频激光干涉仪进行在线精密测量,2个激光干涉仪发射器平行置于导轨两侧,发射器对应的反射镜固定在滑台上,并随滑台一起运动。激光通过反射镜反射后,在嵌于激光头内的探测器中形成干涉光束,进而实现对直接进给轴的位移测量。 图4 试验平台伺服控制系统框图Fig.4 Servo control system block diagram of experimental platform 试验平台控制系统的驱动控制原理如图4所示,通过开发环境编写的控制程序在上位机运行后,上位机便将程序指令通过PCI总线发送给运动控制器。运动控制器在接收指令后完成相应的实时运动规划,并将运动信号发送给驱动器,伺服驱动器控制直接进给轴的运动。同时通过编码器测量实际的位移量并反馈给运动控制器,运动控制器将理论值与实际值相比较,通过差值信号调节电机运动误差,构成了全闭环式的伺服系统,实现了高精密电机驱动控制。 在设定位移一定的条件下,运动时间t的大小是直接进给轴加速度饱和性能的重要表现形式,运动时间t包含两部分,即加速时间和匀速时间。当加速度饱和性能越强时,到达目标速度的时间越短;开始匀速运动的时间节点越早,运动时间t越短。试验中,进给轴在位置模式下进行位置规划运动,设置进给轴的目标距离为100 mm,目标速度为0.5 m/s,目标加速度为0.4g。通过位移数据采集软件设置高频采集模块的采样率为5 000 Hz,采集时间为2 s,由位移的起始和结束对应的采样点可以得到运动时间t的数据样本。同时,每隔两个间隔采样点,对采集到的位移数据进行平均时间值处理,由此得到运动速度的数据样本。 本文应用正交试验设计方法,对自变量伺服参数进行选定,从全面试验中挑选出部分有代表性的点进行试验,该试验设计方法具备“均匀分散,齐整可比”的特点。借助于SPSS统计工具,设计出三因素六水平正交表,其中,水平因子的取值情况见表1。 表1 正交试验水平因子分布情况Tab.1 Distribution of horizontal factors 经过上述试验,可以得到不同伺服参数下运动时间t和速度超调量σ的样本数据库,应用偏最小二乘回归方法,构建运动时间t和速度最大超调量σ关于位置环比例增益Ks、速度环比例增益KPv以及速度环积分KIv的关系模型,可得 t=(3.058 8×102)+(1.633 7×10-2)Ks+ (18) σ=(1.110 7×102)-(9.596 1×10-2)Ks- (19) 以式(18)为适应度函数,在速度超调量不大于5 mm/s的约束下,通过粒子群算法,辨识优化参数,最终通过PSO算法优化得到的解为:Ks=793.62,KPv=1.15,KIv=6×10-5。该优化解对应的适应度值为3.189×102。 为了验证应用偏最小二乘回归建立的运动时间t和速度超调量σ的数学模型的预测精度,随机选取200组样本,进行了模型的预测性能测试,设置预测数据与试验所得数据的差值为预测偏差值,通过统计分析,得到图5所示的模型预测效果图。从图中可见,运动时间t的偏差均值为0.20 ms,预测偏差值可控制在±1 mm/s以内,最大偏差为0.80 ms;速度最大超调量σ的偏差均值为0.21 mm/s,预测偏差值可控制在±1 mm/s以内,最大偏差为0.92 mm/s;且运动时间t和速度最大超调量σ的标准差分别为0.15 ms和0.18 mm/s,都比较小,由此可见,运动时间t和速度最大超调量σ的模型精度较高。 图5 模型预测效果图Fig.5 Prediction performance of PLS model 为了验证通过PSO算法辨识得到的优化参数的有效性,随机选取200组试验参数进行比较,其中一组为优化辨识得到的伺服参数,试验条件皆与样本建立时所采用的试验条件相同。将最终得到的运动时间t和速度最大超调量σ的数据进行对比,得到如图6所示的运动时间与速度最大超调量试验结果对比图。 图6 运动时间与速度最大超调量对比图Fig.6 Comparison of motion time and velocity overshoot 图6为运动时间t与速度最大超调量σ的试验结果对比图。P点和Q点分别表示优化参数下运动时间t和速度最大超调量σ的试验结果。 从图6中运动时间t和速度最大超调量σ的总体趋势可以看出,运动时间t较大时,对应的速度最大超调量σ较小;速度最大超调量σ较大时,运动时间t较小;该结果是与系统的快速响应特性和振荡性能之间成负相关的事实相吻合的。以优化得到的试验序列位置P和速度最大超调为基准,对图6中表示的试验结果分4种情况讨论:①高于P运动时间的虚线区域;②低于P运动时间的虚线区域;③超过速度最大超调可行分界线(σ=5 mm/s)的区域;④低于速度最大超调可行分界线的区域。由图6可知,小于P点运动时间的点,其对应的速度最大超调量都高于该分界线,不满足优化条件,但P点试验的超调量满足条件,且达到最小值。 为了统一量纲和更直观地体现优化伺服参数的效果,对不满足优化条件的运动时间值进行惩罚,在数据处理环节中,引入综合考虑运动时间t及速度最大超调量σ的评价因子ξ: (20) 式中,C1为惩罚常数,C1=0.05;Et为运动时间t的均值;C2为调节常数,C2=0.5,根据运动时间t的下界对评价因子ξ进行调节;σ0值取5 mm/s。 当σ>σ0时,ξ=C1;σ<σ0时,ξ值越小,表示直接进给轴的加速度饱和性能越好,由此可得图7所示的评价因子效果图。 图7 评价因子效果图Fig.7 Evaluation factor rendering 图7中,W点表示优化参数的综合试验结果。由图7可以看出,与其他满足优化条件的试验数据相比,W点对应的ξ值最小,表现出最好的加速度饱和性能。将图中W点的值(4.6×10-3)与样本组的平均驱动性能指标(1.45×10-2)进行比较可得,优化伺服参数的加速度饱和性能比样本组的平均加速度饱和性能指标高68%。综上可知,本文提出的直接进给轴加速度饱和性能优化方法是可行的,能有效提高直接进给轴的加速度驱动性能。 本文对直接进给轴加速度饱和性能的优化方法进行了研究,分析了伺服加速度的影响因素,在直接进给轴试验台上开展加速度饱和性能测试研究,通过偏最小二乘回归方法建立运动时间和速度最大超调量关于伺服参数的模型,运用粒子群算法辨识加速度饱和性能优化的伺服参数。通过对比模型预测结果和试验结果,直接进给轴加速度饱和性能模型能够准确地预测加速度饱和性能。在自构建的直接进给轴试验平台上进行随机试验验证,结果表明:混合优化结果得到的伺服参数具有较好的加速度饱和性能,不但满足速度超调量的要求,而且比样本组的平均驱动性能指标高出68%,说明混合偏最小二乘回归与粒子群优化的直接进给轴加速度饱和性能优化方法是可行的。
3 加速度饱和性能的优化
3.1 优化引擎
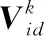
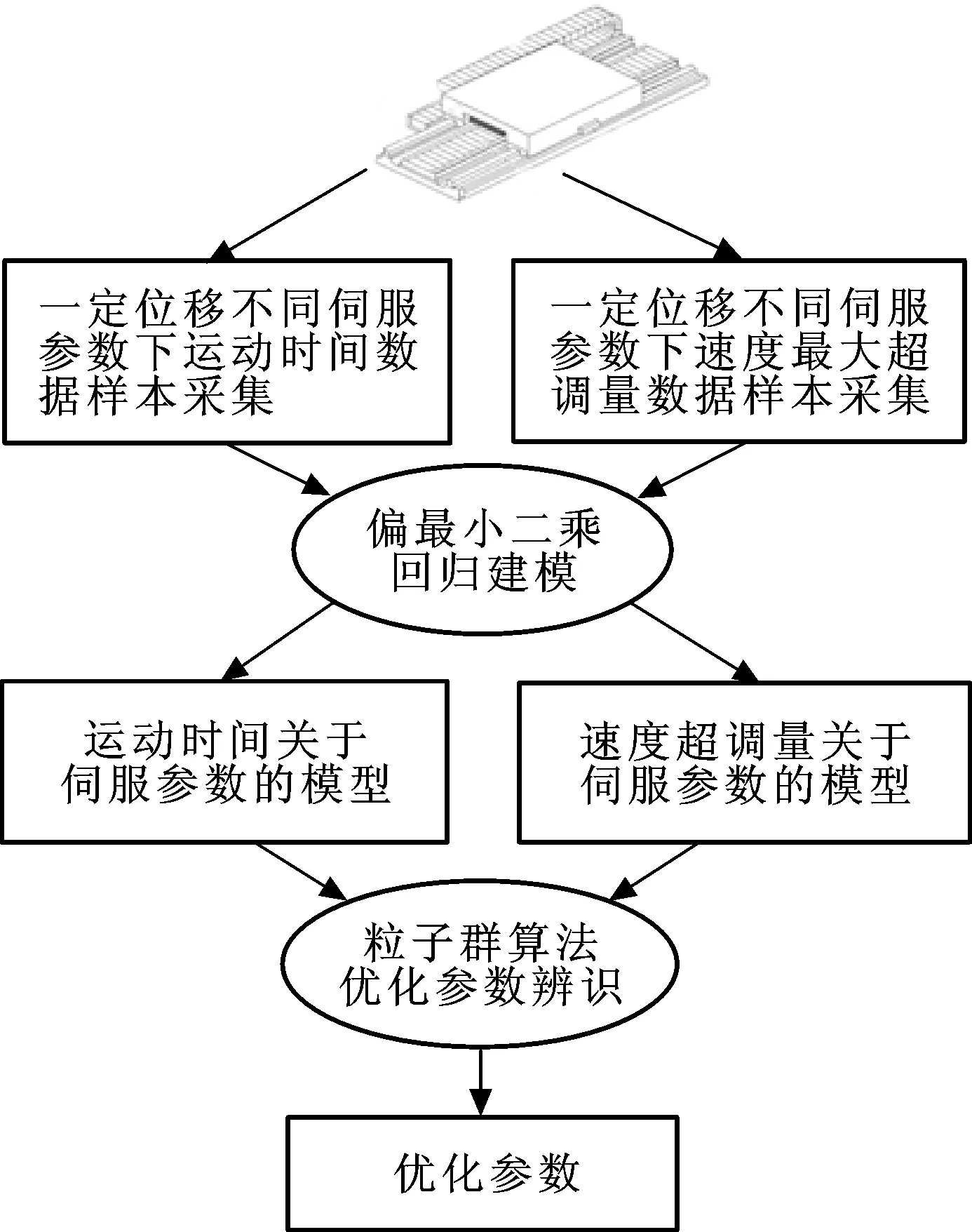
3.2 优化方法
4 试验研究
4.1 试验平台的建立


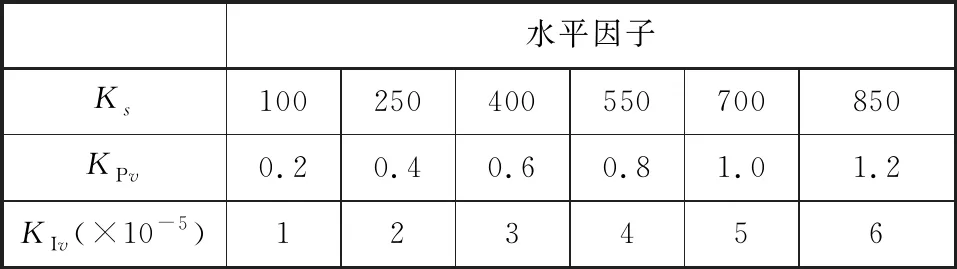
4.2 试验方案的设置
4.3 试验结果与分析
(4.214 3×10-1)KPv-6.946 4×103)KIv
(2.081 9×101)KPv-(8.217 4×104)KIv

5 结论

