基于A-INS组合导航的现代有轨电车轨道几何状态快速精密测量

周禹昆,陈起金,牛小骥

(武汉大学卫星导航定位技术研究中心,武汉 430079)

随着城市现代化节奏加快，交通拥堵问题日趋严峻，现代有轨电车因其容量大、造价低、节能环保、舒适便捷、运营灵活等特点成为各大中城市轨道交通方式的首选[1-3]。武汉市首条现代有轨电车试验线采用超级电容储能式有轨电车，运营长度63.6 km，设计最高运行速度为70 km/h，如图1所示。有轨电车铁轨在列车动荷载的反复作用下，轨道结构的几何形状、位置和尺寸逐渐偏离其正常状态，形成各种轨道变形，即各类轨道不平顺。轨道的几何状态直接关系到有轨电车的运行安全、行车速度、平稳舒适性和车辆部件寿命等，并关系到设计、施工、维修等各部门的工作和运输成本[4-7]。因此，测量轨道几何不平顺对于整个轨道的维护具有极其重要的意义。

图1 武汉有轨电车线路

目前，国内外多采用全站仪配合手推式轨检小车进行铁路轨道建设和运营维护阶段的轨道几何平顺性的检测，如瑞士GRP1000轨检小车和Trimble GEDO CE轨道测量系统[8]。国内目前自主研发基于全站仪的轨检小车主要有广州南方高速铁路测量技术有限公司、江西日月明测控科技股份有限公司、成都普罗米新科技有限公司、中铁工程设计咨询集团有限公司等[9-13]。该系统通过高精度全站仪在轨道控制网下设站，采集轨道的三维位置坐标，可以在“走走停停”的测量模式下实现1 mm的绝对测量精度。然而，以全站仪为核心的轨道不平顺检测系统测量效率偏低，每小时只能检测大约150 m的轨道，无法在有轨电车的天窗时间完成维护工作；同时，全站仪的测量精度很容易受到外部环境的影响，如温度和光照条件等[14]。在这种情况下，亟待一种快速实现有轨电车轨道几何状态精密测量的方案，在短时间内完成轨道几何不平顺性的检测。本文提出一种基于带有辅助信息的惯性导航系统(A-INS)测量轨道几何状态的方法，通过在轨检小车上搭载高精度惯导系统以及其他辅助传感器，采用连续移动测量的模式获取有轨电车轨道的几何平顺性参数，测量速度可达5 km/h。相比于传统基于全站仪的轨检小车，该测量系统在保证亚毫米级相对测量精度的同时，极大提高了测量效率，缩短了作业时间。

在过去的研究中，惯性器件被广泛应用于铁路轨道几何状态的监测中，包括轨道检测车和车载式轨道测量仪。现代轨道检测车普遍采用惯性基准法，车体相对于其惯性基准线的位移通过加速度计测的车体加速度二次积分获得，车体与轴箱间的位移可用位移传感器测得。轨道检测车能够有效评估轨道的整体状况，但是难以精确确定轨道变形发生的位置，其里程定位精度只能做到1 m左右，同时其装备率和便利性不足以支撑工务部门的日常养护工作，不适用于局部路段的轨道几何状态精密测量。车载式轨道测量仪的典型方案是将加速度计、陀螺仪和位移传感器等设备安装在列车的刚性结构上，例如轴箱、转向架和车身，通过积分运算推算轨道不平顺参数[15-19]。由于加速度计和陀螺仪值存在测量误差，为克服精度发散的问题必须使用高通滤波器，而这又不可避免地使所测得的轨道不平顺波形存在失真的问题。带有辅助信息的惯性导航技术(A-INS)通过卡尔曼滤波器，利用GNSS的绝对定位结果和其他辅助传感器的观测信息来抑制惯性导航系统的误差积累[20]。

本文首先阐述基于A-INS组合导航系统的有轨电车轨道几何状态精密测量基本方案和相应算法；然后以武汉有轨电车线路实测数据为例，评估本系统测量的精度。

1 基本测量方案

1.1 有轨电车轨道几何状态参数

有轨电车轨道几何状态指的是轨道几何形态和位置，轨道不平顺测量和轨道精调所关心的几何状态参数主要包括轨距、超高、轨向不平顺和高低不平顺。对于武汉现代有轨电车轨道对应的槽型轨来说，轨距定义为左、右两股钢轨头部内侧轨顶面下0～14 mm内作用边之间的最小距离，如图2所示；超高是指同一里程断面左、右轨顶面相对于参考水平面的设计高差，可通过测量对应的倾角得到；轨向不平顺为钢轨内侧面沿轨道延长方向的横向凹凸不平顺，会使车轮产生横向运动，引起现代有轨电车的左右摆动；高低不平顺是钢轨顶面沿轨道延长方向上的垂向凹凸不平顺，会激起车辆的垂向振动，并在轮轨间产生很大的垂向作用力[14,21]。目前，对于铁路轨道快速检测与准确评估来说，轨距和超高的不平顺测量技术已经相对成熟，轨道几何状态精密测量的主要挑战在于高精度轨向不平顺和高低不平顺信息的获取，需要满足亚毫米级的相对测量精度要求。

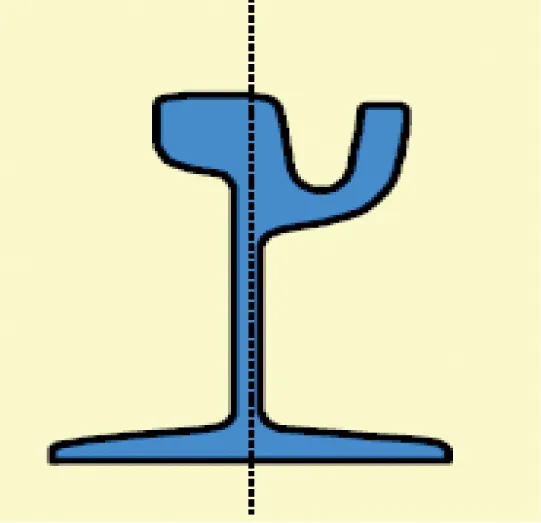
图2 武汉现代有轨电车的槽型轨道

1.2 基于A-INS的轨检小车测量原理

现代有轨电车的钢轨本质可看作一条三维空间曲线，其几何形状可用三维坐标来描述。实际的轨道由于存在变形，其坐标和姿态角等信息也会偏离其设计值。轨道变形改变了轨道各里程点之前的相对几何关系，因此，轨道不平顺本质上是通过钢轨的三维坐标和姿态评估检核点间的相对位置关系。

惯性测量单元(IMU)感知载体(轨检小车)的运动状态，通过对加速度计和陀螺测量值进行机械编排运算，获取载体的位置、速度和姿态信息。惯性导航系统可以跟踪载体的任何机动运动，导航输出数据平稳，具有极高的相对测量精度。但是由于惯性器件噪声的影响，惯性导航系统自主推算的位置、速度和姿态的误差会不断积累下来，严重影响到测量的准确性。带有辅助信息的惯性导航系统(A-INS)可以通过外部观测信息(如GNSS位置信息，里程计辅助)，校正惯性导航系统的误差积累，在较长时间内维持极高的相对测量精度，实现有轨电车轨道几何状态精密测量[20,22-23]。

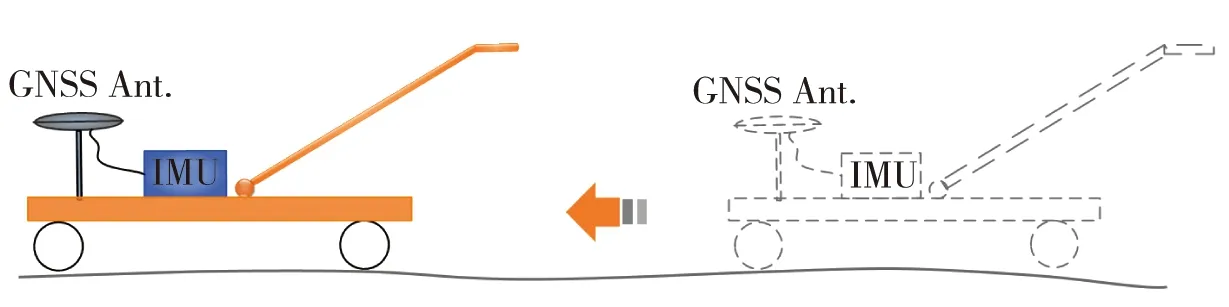
图3 A-INS轨道几何状态测量系统示意

在现代有轨电车轨道几何状态的移动精密测量过程中，惯性测量单元和其他辅助传感器搭载在轨检小车上，与其刚性固联。同时，轨检小车的行走轮与钢轨始终保持刚性接触，保证小车的轨迹线能够真实有效反映实际轨道的几何形状，如图3所示。当轨检小车在现代有轨电车轨道上运动时，轨道变形会引起小车车架运动状态的变化，从而被与小车固联的A-INS组合导航系统感知和测量出来。A-INS轨道几何状态测量系统的基本原理是，以惯性导航系统和辅助传感器为核心测量设备，在动态条件下快速测量轨道的位置、姿态和轨距，据此计算出轨道不平顺测量所关心的轨道几何参数。

2 数据融合算法

针对有轨电车轨道几何状态精密测量这一特殊应用，设计了基于A-INS的卡尔曼滤波数据融合算法，为了提高GNSS/INS组合导航系统的量测精度，算法中加入了非完整性约束(NHC)和反向平滑算法减小量测误差，达到轨道几何不平顺的测量精度要求。根据A-INS组合导航系统提供的高精度三维位置坐标和姿态信息，可以通过投影计算钢轨的位置坐标和超高信息，然后，拟合得到轨道的偏差量，计算轨道不平顺等轨道几何参数，具体参考文献[24]。

2.1 卡尔曼滤波器

卡尔曼滤波作为一种重要的最优估计理论已经广泛应用于组合导航系统，设计了基于21维状态量的卡尔曼滤波器。其中，惯性导航推算的位置、速度、姿态误差在导航坐标系(n系)下表示，姿态误差采用Phi角模型[25]。详细的惯导机械编排算法可参考文献[25]。

在组合导航解算过程中，惯性传感器的残余误差是影响测量精度的重要误差源，需要在滤波器中进行在线的估计和补偿。由于IMU误差随时间变化缓慢，将上述误差建模为一阶高斯-马尔科夫过程，增广到系统状态量中在线估计。卡尔曼滤波状态量包括位置、速度、姿态误差和惯性传感器误差。具体表示为

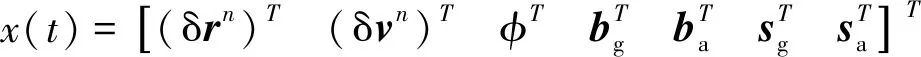
(1)

式中，δrn为在惯性导航系统在n系下的位置误差，δvn为在n系下的速度误差，φ为惯导的姿态误差，b，s分别为IMU陀螺和加速度计的零偏误差和比例因子误差。

卡尔曼滤波器的状态方程可以表示为

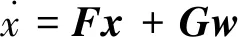
(2)

式中，F为状态转移矩阵；G为系统噪声矩阵；x为系统状态量；w为驱动白噪声。

本文选用GNSS的高精度定位结果作为外部位置观测信息在卡尔曼滤波器中进行更新，用于修正惯性传感器误差。GNSS位置和惯导机械编排推算得到的位置差值作为滤波器的离散观测向量，观测方程为

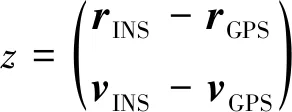
(3)

2.2 非完整性约束

非完整性约束(NHC)一般是指在车辆运动过程中，在不考虑其发生侧滑和垂直跳动的情况下，可以认为车辆在侧向和垂直方向上速度为零。在有轨电车轨道几何不平顺测量中，为了能时刻准确捕获和传递轨道形变量，轨检小车做了特殊的精密机械设计，在轨道上推行时不可能出现垂直跳动和侧向滑动，满足非完整性约束的要求，即轨检小车的垂向速度和侧向速度为零[14,23,25]。

非完整性约束可以作为外部观测信息用作卡尔曼滤波器的量测更新，表示如下

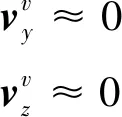
(4)

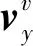
载体坐标系的速度可以表示为

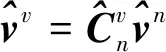
(5)

对上述速度方程做误差扰动，考虑到一阶项，在v系下的速度计算误差模型可表示为

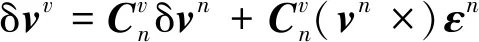
(6)

2.3 反向平滑

为了充分利用A-INS组合导航系统当前和前后历元所有的观测量，进一步地提高测量的精度，在卡尔曼滤波组合导航数据后处理中加入了反向平滑算法。本文采用的反向平滑算法为Rauch-Tung-Streibel(RTS)平滑算法[25-26]。RTS反向平滑算法是一种典型的固定区间平滑线性算法，能够利用过去、当前和未来历元的观测信息计算出比卡尔曼滤波更准确的状态量估计值。算法具体为

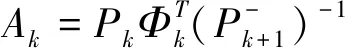
(7)

式中，Ak为增益平滑矩阵；Φ为状态转移矩阵；P为状态误差阵；N为测量历元总数。

3 系统设计

3.1 测量设备

基于A-INS组合导航的有轨电车轨道几何状态精密测量系统主要测量设备包括轨检平台(轨检小车)、高精度惯导系统(INS)、绝对定位模块(GNSS)、轨距传感器和里程计传感器。

3.1.1 轨检平台

轨检平台是整个测量系统的基础部分，用于搭载包括组合导航系统在内的所有测量设备和传感器。轨检小车的车体为刚性结构，3个行走轮与小车固联且与钢轨轨顶面在垂向上保持刚性接触，车体在钢轨的行走轨迹线可以准确反映轨道的实际几何形状。

3.1.2 惯性测量单元

惯性测量单元(IMU)是整个测量系统的核心设备，采用武汉迈普时空导航科技有限公司生产的MP-POS830。该惯导系统由3个单轴激光陀螺仪、3轴高精度石英加速度计构成，测量IMU中心的角速度和加速度信息。POS830内置了NovAtel公司的OEMV-2板卡作为组合导航系统的移动站GNSS接收机，为惯性导航系统提供1 Hz的GNSS观测值信息。表1为POS-830性能参数。

表1 POS830性能指标

3.1.3 绝对定位模块(GNSS)

绝对位置修正对于维持A-INS组合导航系统的相对测量能力和系统精度具有重要意义。在武汉有轨电车轨道不平顺测量中，采用Trimble公司的R9接收机作为GNSS基站，内置在POS830的OEMV-2板卡作为GNSS移动站，通过载波相位的动态后处理模式(PPK)进行GNSS解算，获得高精度的绝对位置修正。在测量作业过程中，基站接收机和移动站同步观测，数据采样率均为1 Hz，在GNSS信号良好的情况下，通过PPK解算实现移动站厘米级的绝对定位精度。

3.1.4 里程计传感器

里程计传感器主要是测量轨检小车沿轨道行进的纵向距离。里程信息是轨道测量中的重要量测信息，可以精确定位轨道不平顺信息，提高空间对齐基准精度。同时，里程计输出信号可以转换为沿轨道方向的速度观测值，与非完整性约束(NHC)一起构成轨检小车的三维速度约束，在GNSS信号受到干扰时，可以有效提高整个组合导航系统的解算精度。

3.1.5 轨距传感器

轨距是轨道几何状态测量的一个重要考察指标，因此需要在轨检小车上集成距离测量传感器，以测定各里程点所对应的轨距信息。轨距传感器安装在小车车体横梁上，可以通过测量车体伸缩杆端弹簧长度变化来测量有轨电车的轨距变化值。

3.2 数据处理方案

基于A-INS组合导航的现代有轨电车轨道几何状态精密测量数据采用武汉大学GNSS中心惯性导航课题组自主开发的InsRail软件进行处理，主要包括A-INS组合导航解算模块和轨道几何状态分析两部分，如图4所示。

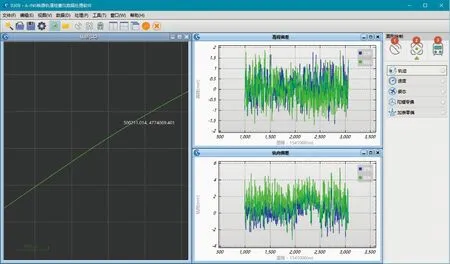
图4 InsRail软件界面

组合导航算法采用松组合模式，支持多种辅助信息与惯性导航的数据融合处理，通过基于21维误差状态向量的卡尔曼滤波器和反向平滑算法以及非完整性约束，可以输出高精度的位置、速度和姿态信息。轨道几何状态分析模块根据组合导航解算的轨道三维位置坐标、姿态信息以及轨距、里程计测量值，可以得到轨道内部几何状态参数，包括轨距、超高、轨向不平顺和高低不平顺，用于轨道几何状态的检测和维护。

4 结果及数据分析

图5 现场测试

本次试验区选在武汉现代有轨电车试验线轨道，在试验线上使用轨检小车搭载POS830系统检测有轨电车的槽型轨道几何状态。本次测量轨道长度约2 km，覆盖直线段、缓和曲线段和圆曲线段，如图5所示。在检测过程中，将Trimble NetR9接收机在现代有轨电车轨道施工控制点设站，作为GNSS基站。GNSS基站具有良好的观测环境，基站和轨检小车的基线长度小于2 km。在实验过程中，为评估A-INS组合导航系统测量现代有轨电车轨道几何状态的实际精度，在同一段现代有轨电车轨道进行了3次重复测量，通过3次测量解算结果的重复性来评估测量精度。解算过程主要包括以下步骤：组合导航解算、轨道几何状态分析解算以及不同测回的轨道内部几何参数比较。图6～图9表示对同一段现代有轨电车轨道3次重复测量解算结果的轨道几何参数差异比较，包括轨距和超高偏差以及沿轨道延长线横向和垂直方向的偏离值，其中，各图中的图(a)表示第一测回的轨道几何参数测量值，图(b)表示第二测回和第三测回几何参数测量值相对于第一测回的差异。图10表示三个测回中第二测回和第三测回的轨向不平顺和高低不平顺(30 m弦，5 m检核点对)相对于第一测回的差异。

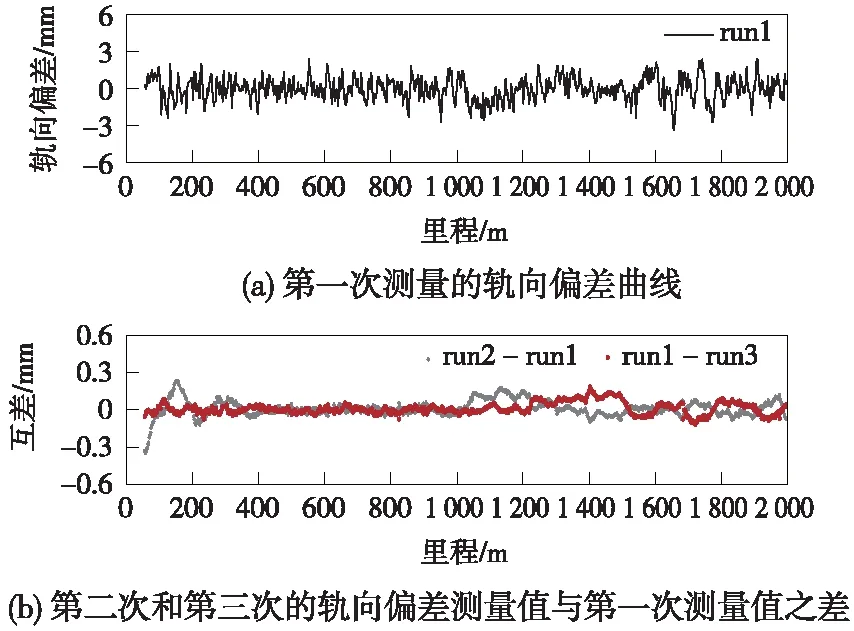
图6 轨向偏差测量值

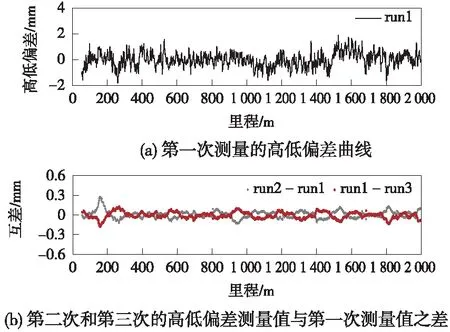
图7 高低偏差测量值

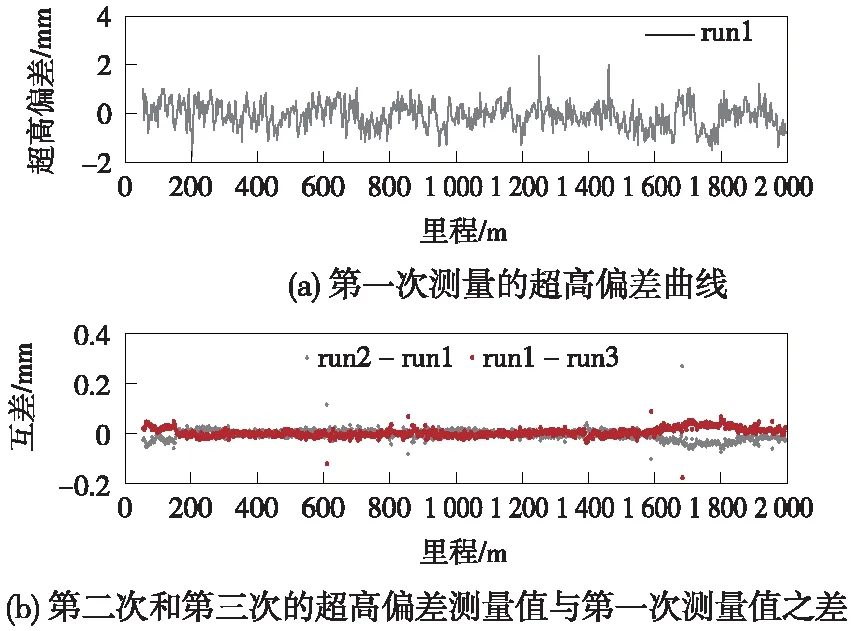
图8 超高偏差测量值

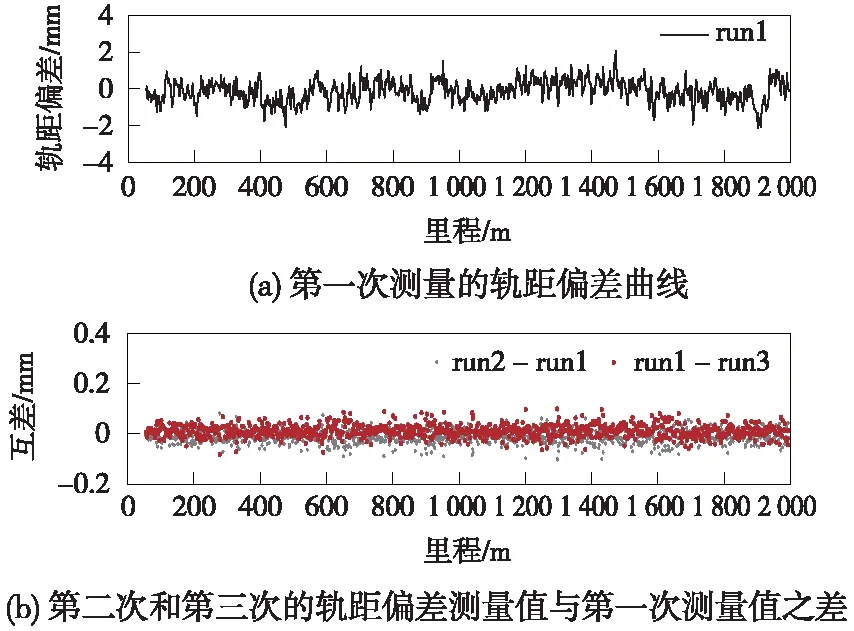
图9 轨距偏差测量值

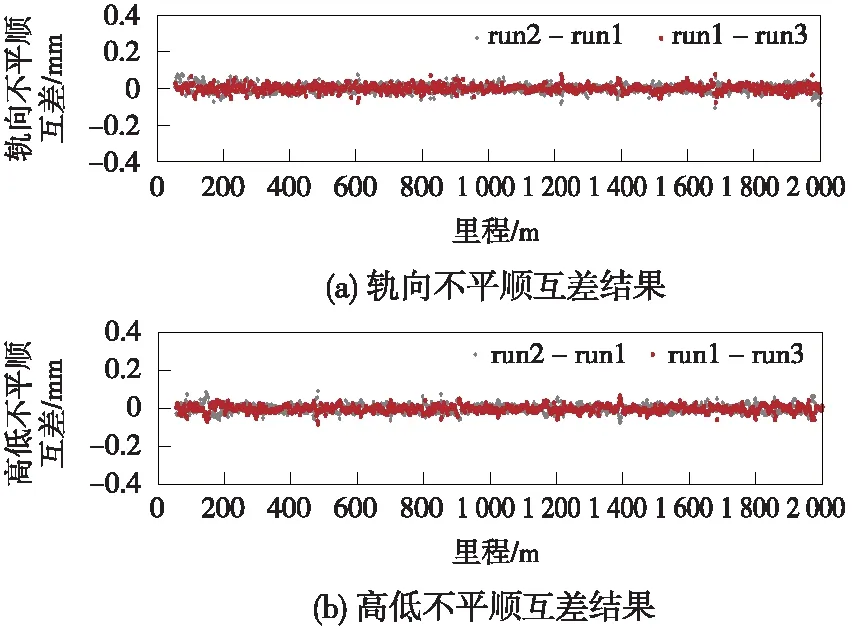
图10 不平顺(30 m弦，5 m检核点对)测量值

从图中可以看出，基于A-INS组合导航的轨道几何状态精密测量系统可以达到亚毫米级的重复测量精度。同一段现代有轨电车轨道三次重复测量的轨道几何参数解算结果显示，被测轨道的超高和轨距偏差的重复测量误差小于0.2 mm，轨向和高低偏差的重复测量误差整体不大于0.3 mm，轨向不平顺和高低不平顺重复测量误差小于0.2 mm。实测结果表明，基于A-INS的组合导航技术可以满足现代有轨电车几何状态精密测量的精度要求。

5 结论

本文提出了一种基于A-INS组合导航技术的轨道几何状态快速精密测量方法及其现代有轨电车轨道不平顺检测的应用。该测量系统采用轨检小车作为移动平台搭载惯性测量单元和其他辅助传感器来获取轨道高精度、高稳定性的位置、速度和姿态信息，来评估轨道的几何状态。在施工作业中，该系统具有很好的稳定性，不依赖施工控制网坐标，可以在5 km/h的速度下完成轨道几何状态精密测量任务，相比于传统基于高精度全站仪测量系统，极大提高了测量效率。在武汉有轨电车的轨道几何状态重复测量结果表明，该系统可达到0.2 mm的重复测量精度，满足现代有轨电车轨道不平顺测量的精度要求，具有较大的测量精度潜力和应用前景。