基于改进型扰动观察法的MPPT 控制策略研究

楼伯良，吴 俊，黄弘扬，马智泉，徐群伟

（国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

随着人类环保意识的增强，新能源受到的关注越来越广泛。太阳能作为新能源的一个分支，具有取之不尽，用之不竭的特点[1-2]。如何有效利用太阳能成为当下研究的焦点和热点，而光伏发电作为利用太阳能的一个有效途径，怎样提高太阳能转化效率的问题得到国内外专家的广泛关注，因此，MPPT（最大功率点跟踪）技术应运而生。

当前，相关领域专家和学者对MPPT 的研究越来越广泛，各种MPPT 算法层出不穷。文献[3]对传统扰动观察法进行了优化，当相邻时刻的功率变化较大时采用大步长，功率变换较小时采用小步长，有效提高了跟踪效率。文献[4]所提出的功率预测变步长扰动观察法能很好地解决跟踪速度和稳态精度的矛盾，外界环境突变时，具有较强抗干扰能力。文献[5]把光伏系统输出功率变化区间划分为3 个区段，通过判断区间来选择步长，有效提高了跟踪效率。文献[6-9]分别采用了模糊控制、神经网络控制、自适应控制和克隆选择算法，均能实现又快又好的控制。但是由于算法复杂，难以在实际中得到大范围推广，目前多限于实验室仿真和理论研究。本文提出了一种基于恒定电压法结合扰动观察法的MPPT 复合控制策略，此复合控制策略就是对传统恒压法和扰动观察法取长补短，实现动态响应速度和稳态精度的共存。

1 光伏电池数学模型简化

1.1 光伏电池电路模型

由文献[10]通用光伏电池模型得到光伏组件等效电路模型，如图1 所示。

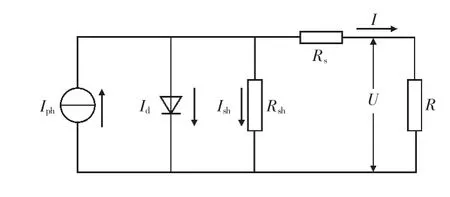
图1 光伏电池电路模型

PV 电池的I-U 输出如式（1）所示：

式中：Io为反向饱和电流；Iph为光生电流；I 为光伏电池输出电流；Rs为等效串联电阻；Rsh为等效旁漏电阻；T 为绝对温度；A 为二极管因子；系数K=1．38×10-23J/K；电荷量q=1．6×10-9C。

为得到简化光伏电池模型，此处仅需4 个参数，分别为开路电压Uoc、短路电流Isc、最大功率点对应电流Im和最大功率点对应电压Um，就可以描述光伏电池特性，Uoc，Isc，Im和Um均是在标准情况（S=1 000 W/m2，T=25 ℃）下所得。简化式（1）可得：

1.2 PV 组件的输出特性

在Matlab2017b/Simulink 平台上通过搭建光伏组件模型，可得到不同光照和温度条件下的P-U 输出特性曲线，如图2 所示。由图2 可知，任意一个温度和光照都会对应一条单峰值的曲线，这个峰值点即为MPP 点，该点会对应一个电压值，即为Um。光伏组件要时刻进行最大功率输出，就需要对曲线的峰值点进行跟踪，因此，需要通过MPPT 技术实现。

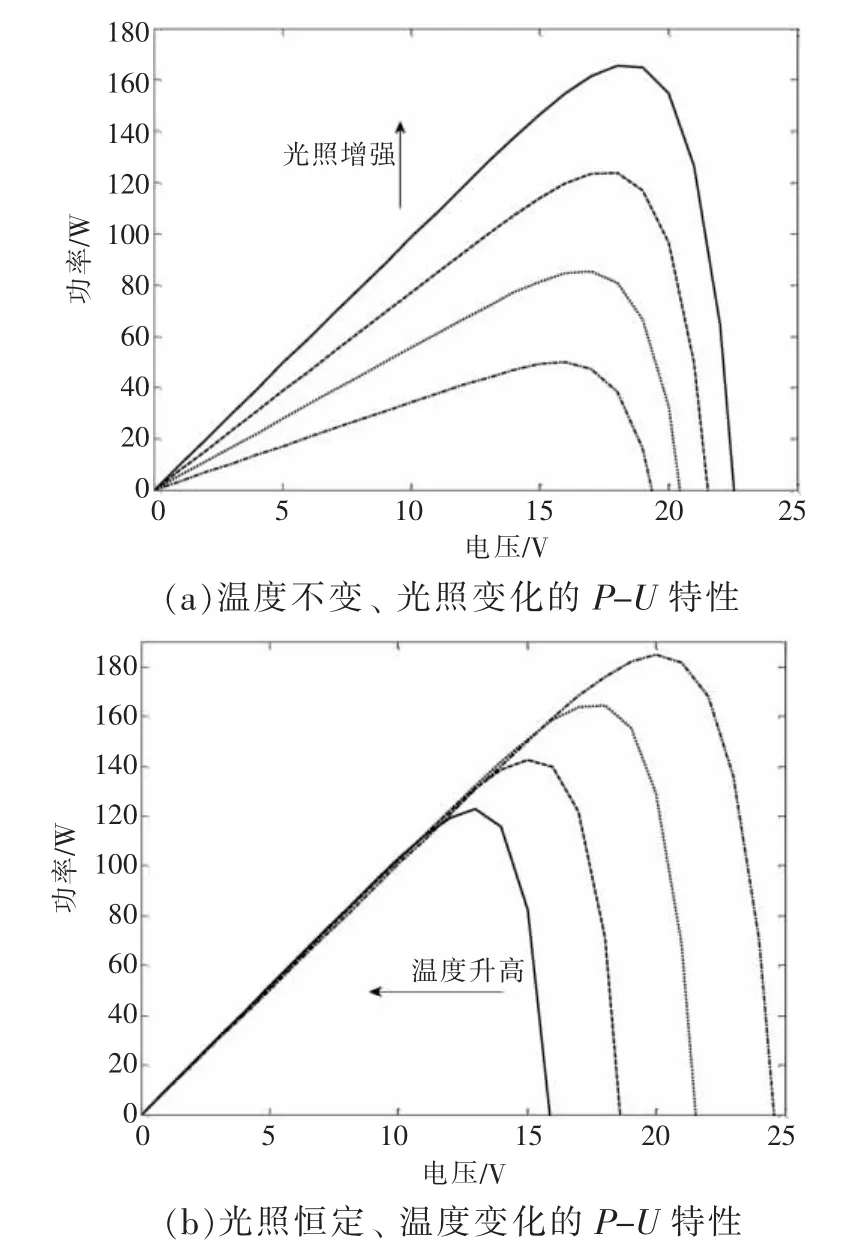
图2 温度、光照变化条件下的PV 组件输出特性曲线

2 传统扰动观察法控制策略

传统扰动观察法的工作机制是通过在相邻时刻对PV 组件输出电压施加一个正向扰动ΔU，判断扰动前后时刻输出功率的变化量ΔP，如果ΔP 大于0，则表示最大功率点位于当前工作点的右侧，还需要继续保持正向扰动；反之，则反向扰动。扰动观察法流程如图3 所示。由图3 可知，扰动观察法工作机制虽然可以实现最大功率点跟踪，但是步长ΔU 难以选择，若ΔU 过大，跟踪速度加快，但是会造成稳态震荡问题，降低光伏系统的效率；若ΔU 过小，虽然减轻了稳态震荡，但是存在动态响应速度迟滞问题。因此，常规扰动观察法不能同时兼顾跟踪速度和稳态精度。

3 基于恒压法结合变步长扰动观察法的MPPT 控制策略

由第2 节分析可知，传统扰动观察法采用定步长，会难以同时兼顾响应速度和稳态精度问题。为了解决此问题，本文提出一种基于恒压法和变步长扰动观察法的MPPT 复合控制策略，复合控制策略流程如图4 所示。

（1）恒压法和变步长扰动观察法的工作机制。由图2（a）的P-U 特性曲线可知，曲线的MPP 点基本近似分布于一条垂直于x 轴的直线两侧，一般满足Um=0．8Uoc作为光伏组件初始电压值[11]，利用此关系可以达到快速定位MPP 附近区域的目的，可极大地加快响应速度。另外，从图2（a）的P-U 曲线还可以看出，远离MPP 时，斜率较大；越接近MPP 时，斜率越小，峰值处，斜率为0。因此，变步长扰动观察法首先实时检测相邻时刻的I（k），I（k+1），U（k）和U（k+1）；其次计算出P（k），P（k+1），dP 和dU。由数学关系可知，在远离MPP 时，dP/dU 越大；在接近MPP 时，dP/dU越小。 因此A=dP/dU 可以作为步长实时调整因子，以A×ΔU 为步长。在恒压法切换到变步长扰动观察法后，在MPP 附近可以对MPP 进行精确定位。恒压法和变步长扰动观察法的控制流程图如图4 所示。

（2）新型MPPT 算法工作机制。启动时，利用恒压法先快速定位到MPP 附近，再启动变步长扰动观察法，根据实际工作点离MPP 的位置，实时计算出步长。当实际工作点离MPP 相对较较远时，MPP 步长越大，可加快追踪速度；当实际工作点离MPP 相对较较近时，MPP 步长越小，可以对MPP 进行精确定位，降低震荡程度。可以实现跟踪速度与跟踪精度的兼顾。

图3 传统扰动观察法控制流程

图4 基于恒压法和变步长扰动观察法的控制流程

4 仿真模型搭建与结果分析

在Matlab R2017b/Simulink 平台上搭建基于Boost 电路的复合MPPT 控制模型，如图5 所示。Boost 电路器件参数设置：电容C1=120 μF，电容C2=450 μF，电感L=15 mH，负载R=55 Ω。PV 组件的仿真参数设置：Uoc=29．96 V，Isc=7．79 A，Um=23．64 V，Im=6．05 A。另外，当标准情况下（S=1 000 W/m2，T=25 ℃）[12-15]，光伏组件最大输出功率输出约为143 W，Simulink 仿真总时间为2．4 s，大步长扰动观察法的步长为0．05 s，小步长扰动观察法的步长为0．000 1 s。

在仿真中，光照强度的变化趋势可以自行设置，这里设置为：启动阶段，S=1 000 W/m2，t=0．8 时，光照强度突变为S=300 W/m2；t=1．6 s 时，光照强度再次突变为S=500 W/m2。Simulink 仿真中，分别对大步长扰动观察法、小步长扰动观察法和恒压法结合变步长扰动观察法进行仿真对比，3 种算法控制条件下的输出功率波形如图6—8 所示。

由图6 可知，启动阶段，标准情况下（T=25 ℃，S=1 000 W/m2）时，在大步长扰动观察法条件下，启动迅速，仅用0．076 s 即可达到新稳态，稳态时的输出最大功率为141．2 W 左右且震荡幅度较大，这是由于步长选择大造成的，会降低光伏电池输出效率；当t=0．8 s 时，光照突变为S=300 W/m2，到达新的稳态用时约为0．07 s，响应速度较快；选取2．1～2．3 s 时段的局部放大图可以清晰看出，在S=600 W/m2的稳态条件下，光伏组件的输出功率在93．4～88 W 之间震荡，震动幅度较大。

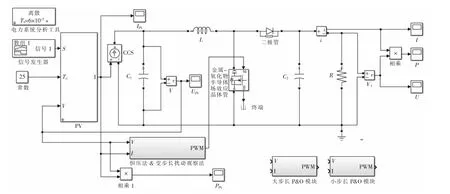
图5 基于Boost 电路的复合MPPT 控制模型

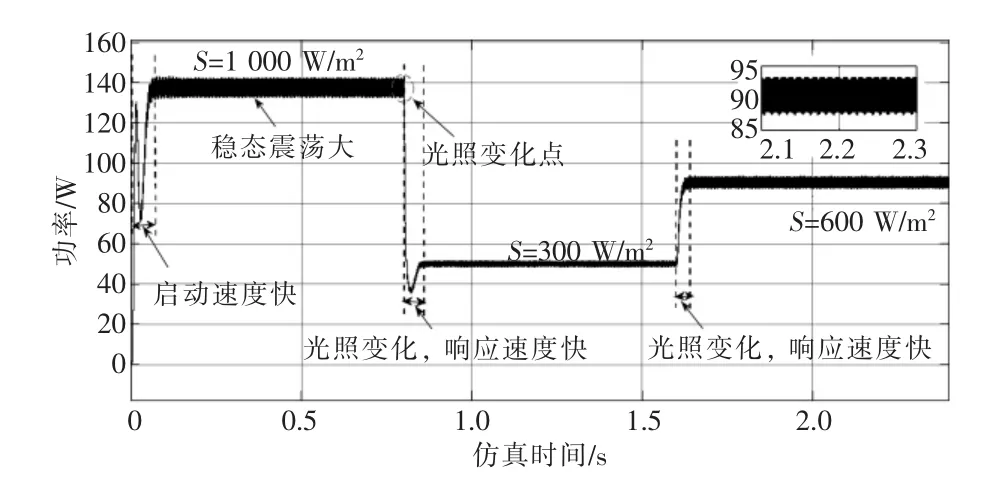
图6 基于大步长扰动观察法MPPT 控制策略输出功率波形

由图7 可知，在小步长扰动观察法控制条件下，启动阶段用时约为0．55 s，启动反应缓慢，到达稳态后的输出最大功率为142．5 W 左右，且震荡幅度很小；当t=0．8 s 时，光照突变为S=300 W/m2，到达新的稳态用时约为0．18 s，响应速度慢；选取2．1～2．3 s 时段的局部放大图可以清晰看出，在S=600 W/m2的稳态条件下，光伏组件的输出功率在92～93．5 W，震荡区间很小。

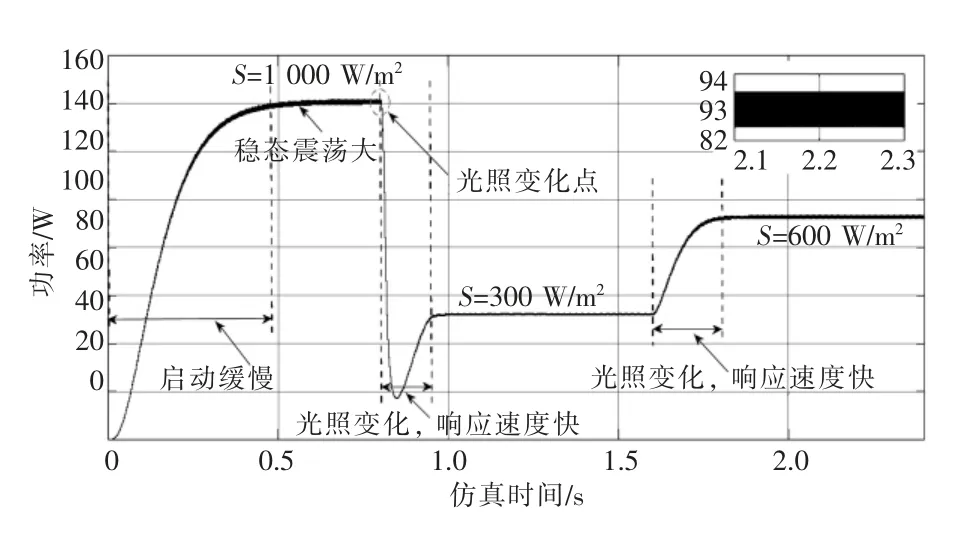
图7 基于小步长扰动观察法MPPT 控制策略输出功率波形

由图8 可知，在恒压法结合变步长扰动观察法控制条件下，启动阶段，恒压法首先起作用，利用Um=0．8Uoc关系式可准确快速定位到最大功率点附近区域，随后切换到变步长扰动观察法对最大功率点进行精确定位。由图8 还可以看出，启动到新稳态用时仅为0．078 s，达到稳定时，最大输出功率约为142．7 W，且震荡幅度很小，稳态精度高；当t=0．8 s 时，光照突变为S=300 W/m2，到达新的稳态用时约为0．077 s，响应速度较快；选取2．1～2．3 s 的局部放大图可以清晰看出，在S=600 W/m2的稳态条件下，光伏组件的输出功率在92～93．4 W，震荡区间很小，稳态震荡范围与小步长扰动观察法基本一致。

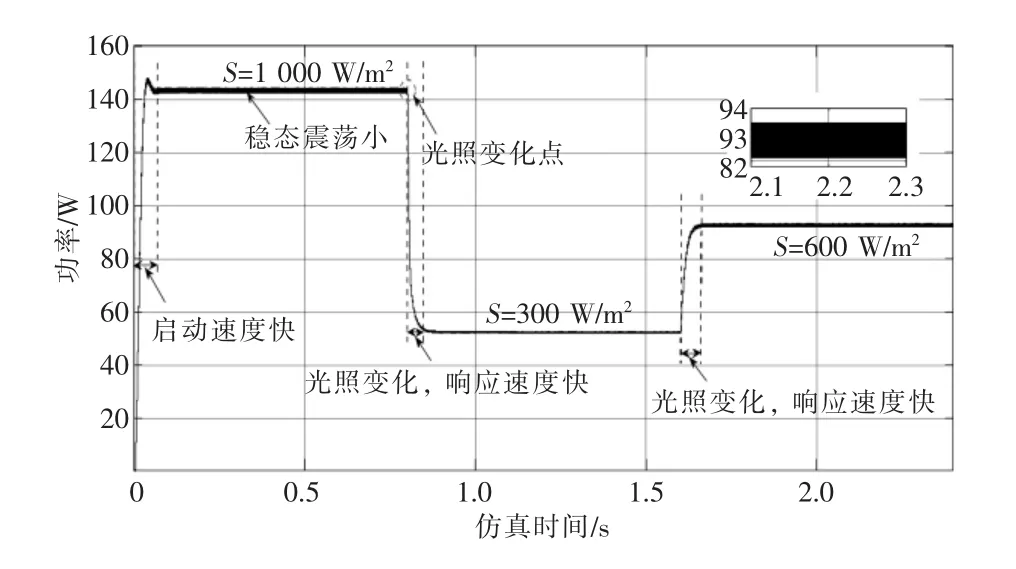
图8 基于恒压法结合变步长扰动观察法的MPPT控制策略输出功率波形

5 结语

针对传统扰动观察法动态和稳态不可调和的矛盾，提出了改进型扰动观察法MPPT 控制算法，通过对恒压法和扰动观察法的取长补短，进行优势互补，有效实现了又快又稳地对MPP 的精确追踪。相比于传统扰动观察法，改进型复合控制策略不但跟踪速度快，而且稳态精度高，具有良好的推广价值。