适应值引导下的粒子群算法群体特性分析

穆华平

（鹤壁技术学院公共基础教研部，河南鹤壁，458030）

0 引言

粒子群算法[1]（PSO）是一种具有适应性的搜索算法，由美国的Kennedy 和Eberhart 教授于1995 年共同研究提出。由于该算法模型简单、收敛速度快并且收敛的精度较其他智能算法要高，因而得到了领域内诸多学者的关注[2-3]。然而随着应用领域的扩展和深入，早熟收敛的问题日渐突出，尤其对于大规模、复杂的多维优化问题，这种弊端就更加突出。由于复杂网络的自适应形成过程和特点与粒子群算法的搜索的驱动力之间具有许多相似之处，本文就适应性引导下的粒子群算法群体特性进行研究，探索提高粒子群算法性能的方法。

1 粒子群算法模型

粒子群算法是将优化问题的潜在解看作一个个没有质量、没有体积的“粒子”，以一定的初速度在解空间中飞行搜索，其搜索的轨迹由自身的状态和飞行中学习其它优秀粒子的结果共同决定[4]。假设规模为N的粒子群体在D维空间中飞行，每个粒子的当前位置为Xi=(xi1,xi2,...,xiD)，当前速度为Vi=(vi1,vi2,...,viD)。粒子根据自身的历史最优位置Pi=(pi1,pi2,...,piD)和邻域内历史最优位置Pig=(p ig1,pig2,...,igD pigD)调整自己的飞行状态，可以得出算法的搜索公式：

公式(1)的第一部分是粒子自身的速度惯性对飞行轨迹的影响；第二部分是粒子的历史最优位置对其飞行轨迹的影响；第三部分是粒子所在邻域内其它粒子对其飞行轨迹的影响。显然，群体的规模大小和连接方式能够影响邻域的范围，进而影响粒子的寻优轨迹。当邻域为整个群体时群体结构为完全连接，邻域内最优位置即为整个群体的历史最优位置；当邻域只包含自身时群体结构完全离散，邻域内最优位置与自身历史最优位置相同。

2 群体网络特征属性

粒子群算法的群体模型实质上是通过粒子在寻优过程中对于搜索经验的借鉴而相互作用形成的关系网络，根据复杂网络的相关理论[5]，同时结合图论的基本概念，抽取能够描述群体网络特点的特征属性来进行研究。

（1）平均最短路径长度

平均最短路径长度是指群体网络中任意两个粒子之间学习经验最少要经历的边数的平均值，它是用来衡量群体内粒子之间信息传播速度的重要性能指标，其定义为：

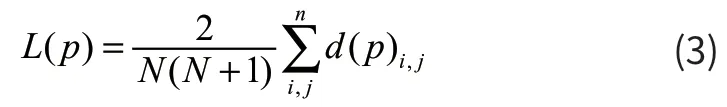
其中，d(p)i,j表示进化概率为P时粒子i和j之间的最少边数。

（2）平均聚集系数

节点的聚集系数描述的是群体网络中与某节点直接关联的所有节点之间的关联度，即所有与某节点直接相连的节点中实际的连接边数占全连接情况下边数的比例。具体定义为：

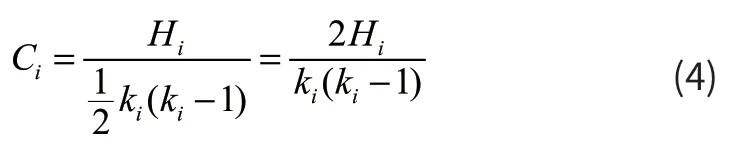
其中，Hi是与节点i直接关联的边的数量；k i(ki-1)/2是最多可能存在的边的数量。由此可以得出整个网络的聚集系数为：

3 以适应值为驱动的群体演化机制

粒子群群体随着算法的搜索，按照适应值的优劣同步完成群体网络的自适应生长。初始化群体为随机网络模型，当搜索陷入停滞状态或者多次震荡性搜索时，根据适应值大小增加或者删除连接，促进算法搜索的同时演化群体结构。

3.1 增删边策略

为了使算法跳出局部最优，获得更佳的优化性能，应当让适应值好的粒子比适应值差的粒子获得更多的连接。因此，算法在进入搜索停滞状态时，要将群体内的所有粒子按照适应值的优劣进行排名，适应值差的粒子在前，适应值好的在后。

定义：第t代时粒子i的排名为：Rank i(t)=Indexθ(Xi(t))，其中Index(X i(t)为粒子适应值排名后的粒子的编号，θ为影响因子，来调节粒子间的排名差距。删除边的概率定义如下：

对于粒子i和j之间的边(i,j)，删除边的概率根据适应值较差的粒子确定。经过多次的删边操作，群体间的连接会大大减少。为了避免出现孤立节点，因而给断边后的节点选择学习对象的机会。增加边的概率定义如下：

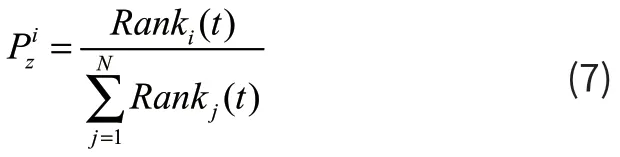
3.2 算法流程

适应值引导下的粒子群算法（Particle Swarm Optim ization Guided by Fitness）的基本流程为：

（1）将粒子按照适应值大小降序排列，记录排序后的每个粒子的排名Rank(t)；根据公式（4）计算群体中删除边的概率；

（2）遍历粒子群体中的所有连接，根据边删除规则删除边，根据边增加规则增加边；

（3）判断迭代次数tMOD20=0 是否成立；

（4）结束条件是否成立，如果成立则停止优化并输出最优值；若不满足，则进化代数t=t+1 。

4 仿真实验

4.1 实验设置

实验选取典型的Rosenbrock 函数来测试群体结构的演化过程。Rosenbrock 函数是一种非常难以优化的单峰病态函数，全局极值点位于一个类似香蕉形的狭长山谷内，xi=1时达到最小值0，其定义如下：

实验设置如下：粒子个数为100，问题维数为50 维。惯性权重ω从0.9 线性递减为0.4，加速因子为1.5，运行环境为Inter i5 CPU，4G 内存，Windows7 系统。函数进化1000 代，每进化200 代记录一次两个特征属性值。

4.2 实验结果与分析

影响因子θ通过调节粒子适应值的排名差距而影响删除和添加边的概率大小，进而达到调整群体进化速度和结构特性的效果，因而对不同的θ取值对于群体结构和算法性能的影响，取θ=1,θ=5,θ=10,θ=20进行对比实验，结果如图1 和图2 所示。

图1 平均最短路径长度变化情况

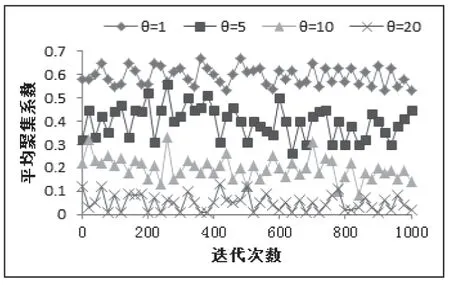
图2 平均聚集系数变化情况

从图1～图2 可以看出，θ=1 时，群体进化过程中边的删除概率较小而增加新连接的概率较大，因而删除边的速度较慢，增加边的速度较快，整个群体结构的聚集系数比较大，这说明群体中节点度小的粒子很少，群体结构接近完全连接，这种结构容易导致算法的局部搜索能力降低，容易引起算法在局部最优位置附近徘徊而难以到达全局极值点。θ=10，20 时，群体结构的聚集系数变小，群体的连接程度变得松散，这有利于算法的细致搜索，然而搜索速度大大下降，全局搜索能力降低，并且由于删除和增加连接边的概率增大，平均最短路径长度出现震荡性变化，进而引起群体模型的大幅度震荡，对历史最优位置的记忆能力减弱，有可能导致算法的稳定性降低，不利于算法的寻优。同时，从图1和图2 的变化趋势看，随着影响因子θ的增加，群体最优粒子能够吸引更多的粒子通过学习与之产生连接，这必然导致解信息在群体中的传输速度不断加快。搜索速度过快，有可能导致算法跨过全局最优位置，导致算法发无法搜索到全局极值，而θ过小则会导致算法在陷入局部极值时没有突破局部极值的外力，搜索范围狭窄而陷入局部最优位置。

5 结论

以适应值为引导的粒子群算法优化过程，同时也是粒子群体结构自适应演化的过程。从仿真结果可以看出在适应值的引导下，群体模型的特征属性表现出自适应的动态变化。在不同的影响因子的作用下，群体网络的平均聚集系数和平均最短路径长度出现较大的差异。这意味着，改变群体结构的特征属性，能够影响潜在解的优化信息的传播方式和速度，进而调整算法的优化方式和性能，是改进粒子群算法性能的一个简单有效的策略。