基于SVM的手写数字识别

陈虹州

（杭州师范大学附属中学，浙江杭州，310030）

1 研究背景

阿拉伯数字作为唯一被世界各国通用的符号，其在各行各业的地位是无可取代的。随着科技的发展，越来越多的数据信息需要被录入于计算机之中随后进行处理，通过人工识别纸张上数字的方法由于效率低下已不适用于海量数据的识别。

作为光学字符识别技术的一个分支，手写体数字识别主要研究内容为如何利用计算机自动辨认手写在纸张上的阿拉伯数字。其可分为脱机手写数字识别和联机手写数字识别，前者无需特定的输入设备，只需将书写好的文字采集到本地机器中，对该图像进行处理，因此占一定的本地空间，识别速度快，但由于缺少笔划顺序等信息因此识别精度较低；而后者则为对书写数字的实时识别，需要通过特定的输入设备，其可记录笔划的顺序等信息。相比于前者，由于获取的信息较多其识别精度较高，但识别速度慢。目前手写体数字识别技术对各行各业发展的影响也越来越大。银行票据、财务报表、邮政编码等都可以通过手写体数字识别进行数字识别，从而提高效率，节省大量的人力、物力和财力。同时，由于手写数字识别实现相对简单，其可作为其他复杂问题、复杂算法的试金石。

虽然阿拉伯数字只有0-9 共10 个数字，且笔画相对简单，但由于各国、各人的手写习惯的不同，以及数字之间的差异性较小，导致手写数字识别的通用性不佳。除此之外，阿拉伯数字常用于银行、财务等方面，因此对其识别的准确性具有很高的要求。综上所述，如何准确、高效、低拒识率地识别出手写体数字一直是研究领域内的热点问题之一。

2 国内外研究现状

手写体数字的识别是光学字符识别的一个分支，早在1929 年，Tausheck 就利用光学模板匹配方法识别数字，1995 年Vapnik 等人建立了支持向量机(Support VectorMachines.SVM)的知识体系，SVM 的出现为基于模式识别的字符识别领域提供了新的工具[1]。在国内，将SVM 应用于手写数字识别领域并进行优化的研究也一直在进行，2005 年杭州电子工业学院的蒙庚祥、方景龙在实验中用基于支持向量机的SMO 的改进算法解决了大训练样本的问题得到了识别速度快、识别效率高的效果[2]。同年长沙理工大学计算机与通讯工程学的张鸽、陈书开用穿越次数特征让识别率有所提高，并且比较了SVM 和bp 神经网络进行手写体数字识别的速度，发现SVM 可以解决bp 神经网络的局部极值问题[3]。2006 年山东师范大学的吴琳琳为解决找到适合多类分类方法和大规模数据集的训练算法设计了SVM.HDR 软件系统，将手写数字的识别过程流程化，再选择合适的核函数，实现了验证SVM 算法的有效性和识误率低的目标[4]。由此可见，目前国内外针对SVM 的手写数字识别的研究内容主要集中于如何利用特征提取、优化SVM算法等方法，提高SVM 识别的准确性以及高效性。

3 基于支持向量机的手写数字识别

3.1 支持向量机简介

支持向量机方法属于经典的有监督机器学习方法，它包含了多种技术知识，如最大间隔超平面、Mercer 核、凸二次规划和松弛变量等，可用于解决二分类问题。针对于样本线性可分的情况，可采用间隔最大化法进行分类。具体内容为，假设给定训练样本集中有n 个样本，即：

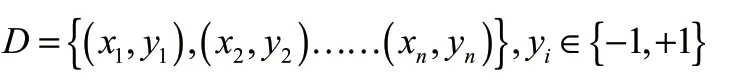
其中xi表示由m 维特征构成的第i 个样本，yi则表示第i 个样本的分类结果。SVM 的基本思想为在已知的训练样本集D 的样本空间中找到一个超平面wTx+b=0，该超平面可以将不同的样本分开，同时使得支持向量（即距离超平面最近的训练样本）到超平面的距离最大化，具有上述特点的超平面则被称为具有“最大间隔”的超平面。求该最大间隔的超平面即找到满足y i(wTxi+b) ≥ 1约束的w 和b，并使得最大。

当原始样本线性不可分时，则可采用合适的核函数将样本特征空间映射到更高维度的样本特征空间中，使得样本在更高维的特征空间内线性可分。SVM 的分类精度会受核函数影响，因此选取合适的核函数是使用SVM 算法的重要内容之一。

由于SVM 是二分类的机器学习算法，即分类结果不是A 就是B，但在现实生活中多为多分类应用场景，为解决二分类向多分类的转换，有一对一（OneVSOne，OVO）和一对其余（Onevs Rest，OVR）两种常用方法。其中OVO 算法解决问题的思路是：假设有n 个类别的分类任务，将这n个类别两两组合，就会产生n（n-1）＊2 个二分类任务。在测试过程中，把新样本同时提交给所有分类器，这样就会得到n（n-1）＊2 个结果，而最终的测试结果会综合所有的结果，把预测的最多的类别作为最为最终分类的结果。OVR 算法则每次训练中选取一个类的样例作为正例，而所有其他类的样例作为负例来训练N 个分类器。在测试时，若仅有一个分类器预测为正类，则对应的类别标记为最终分类结果。

3.2 支持向量机优势

支持向量机拥有诸多优点，主要包括：

（1）切分平面间隔最大化的基本思想使得支持向量机避免了对数据规模，数据分布的依赖，因此对于小样本的机器学习问题有较好的效果。

（2）SVM 将低维的特征维数空间转化为高维维数空间，虽然看似计算更为复杂，但将分类任务的非线性问题转化为线性问题。通过只由少数的支持向量所确定的核函数，不仅解决了维数灾难的问题，同时使得样本维数与算法复杂度解耦。

（3）传统方法会产生过拟合和局部最小等问题，而理论上，SVM 优化方法得到的结果为全局最优解。此外，SVM 在鲁棒性、学习能力、泛化能力方面均较为优秀。

4 支持向量机解决手写数字识别问题基本方法

如图1 所示，基于SVM 的手写数字识别流程主要包括划分数据集、图像预处理、特征提取、训练及测试、分类等主要部分：

（1）划分数据集

进行图像预处理之前首先需要将数据集合理地划分成训练集和测试集，以避免训练过程中的过拟合或欠拟合问题导致识别效果欠佳的现象发生。

（2）图像预处理

图像预处理的目的是便简化识别内容，提高识别精度。预处理包括对图像完成归一化、二值化、去噪等操作。归一化操作包括裁剪和大小规格化，对于一张有数字的图片来说，只有数字才是所需信息，因此要区分出图像区和非图像区，裁剪出图像区后，求得图像中的数字上、下、左、右四个边界点，剪裁掉图像四个方向的边界空白区域，并求出待识别数字的高度和宽度，然后按比例将图像统一缩放为n＊n 像素。随后，进行数字图像的二值化，将数字图像提取后的灰度数字图像转化为二值化图像，以进一步简化计算。转换过程是把n＊n 的图像中的每一个像素点的0-255 灰度值转化为0 或1。最后进行去噪，即将图片中除数字以外的噪点消去，以避免干扰特征向量的提取进而影响数字识别。

（3）特征提取

特征提取在手写数字识别中是非常重要的环节。它的过程是通过映射或变换的方法将数字图像的特征从高维映射到低维。特征提取的方法一般分为两种：结构特征提取以及统计特征提取。结构特征是通过分析字符笔画得到的，对局部特征的区分效果较好，例如笔画密度、交叉点、断点、轮廓等；统计特征则是利用统计方法得到的，包括点密度估计、特征区、矩等。其中具体的方法有粗网格特征及笔划密度特征。粗网格特征指将图像预处理后分成n＊n 的网格，统计每个网格内的黑像素的数量即得到一个以数值表示的网格特征;笔划密度特征则以不同方向扫描数字,计算扫描线与笔划相交的次数。

（4）训练与测试

图1 基于SVM 的手写数字识别流程图

将进行特征提取之后的特征向量集合，将划分之后的训练集用于SVM 模型的训练过程中，由于所提取的特征向量可能线性不可分，因此需利用核函数将特征向量提高至线性可分的维度，随后利用最大间隔超平面的原理，求出支持向量，进一步求得最大间隔超平面方程和决策函数，即训练好的SVM 模型。由于手写数字识别为多分类问题，因此将训练多个SVM 模型以区分不同的数字。随后将测试集应用于训练之后的SVM 模型集合中，获得分类结果并与自身标签相比对，得出识别精度，若精度不满足则调整相关参数再次训练，直至达到理想精度。

（5）分类过程

将待分类的数据集依次输入至训练好的多个SVM 模型中，整合每个SVM决策函数的结果，仲裁该样本的具体类别。

5 实验与结果分析

为比较不同的核函数和解决多分类问题的算法对基于SVM 的手写数字识别实验的训练时间、测试时间以及准确率的影响，本实验首先对MINIST 数据集进行相同的预处理，然后分别使用四种不同和函数和两种解决多分类的方法进行多次训练构造SVM 模型并测试，得出实验结果。为简化编程本实验中使用Python 中提供的sklearn 库实现SVM算法。

5.1 实验设计

实验中首先读取MINIST 数据集中的训练集，对其进行归一化、二值化、去噪的预处理操作，然后利用sklearn 库中SVC 函数的kernel 参数和decision_function_shape 参数分别实现多项式核函数（poly）、高斯核函数（rbf）、线性核函数（linear）、sigmoid 核函数以及OVO，OVR多分类方案，随后进行训练，得出训练时间及SVM 模型集合，最后利用得到的SVM 模型集合对预处理后的测试机进行测试，得出实验精度。

5.2 实验结果

通过多次试验取平均值，本文得到了如图2 所示的折线图。

从图2 的实验结果中我们不难发现以下几点结论（其中实线框中为OVR 实验数据，虚线框内为OVO 实验数据）：

(1)虽然OVR 需训练N 个分类器，而OVO 需要训练N(N-1)/2 个分类器，但每个核函数分别用OVR、OVO 方法时正确率基本相同，而且训练时间也相差不多。这是因为，OVR 的每个分类器均使用全部训练样例，而OVO 的每个分类器仅用到两个类的样例，因此两者的训练时间相差不大，但在类别很多的时候，OVO 相较于OVR 通常所需的训练时间小。

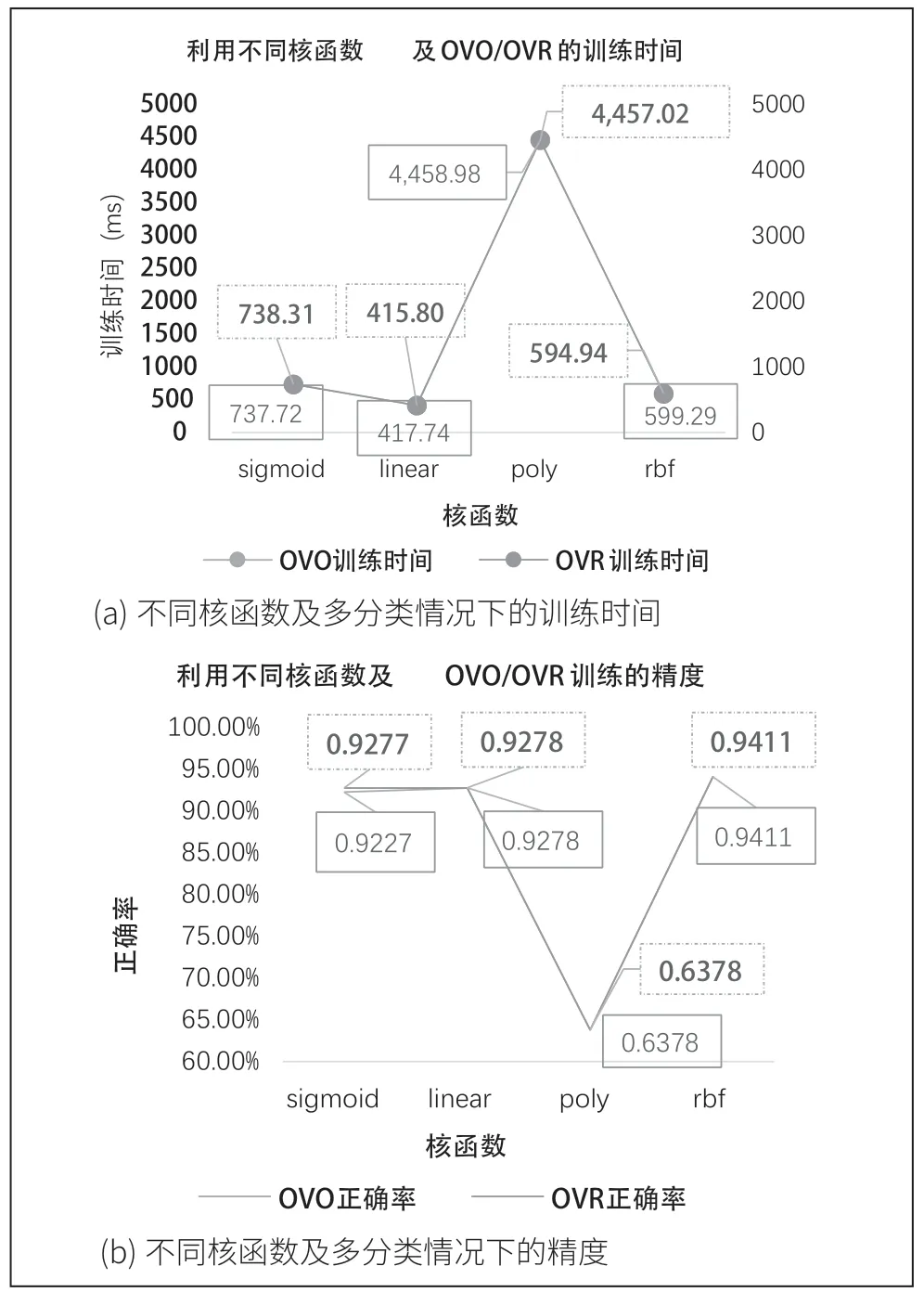
图2

(2)利用四种核函数的正确率：

rbf 核函数＞linear 核函数＞sigmoid 核函数＞poly 核函数

(3)利用四种核函数的训练时间：

linear 核函数

综上，基于SVM 实现手写数字识别问题中，OVO，OVR 两种解决多分类问题的方法效果相近，利用高斯核函数或线性核函数的模型正确率高且时间短，总体较优，而使用多项式核函数时训练时间长、正确率低。

6 总结与展望

本文介绍了SVM 的基础原理以及基于SVM 实现手写体数字识别的基本流程。此外基于SVM 实现了手写数字识别应用，并通过实验得出多项式核函数最不适用于手写数字识别中，而高斯核函数以及线性核函数较为适用，且利用OVO或OVR 解决手写数字识别的多分类问题效果相近的结论。

虽然，实验显示基于SVM 的手写数字识别正确率最高到达94.11%，但对于需高精度的领域来说，还需进一步改善和提升。因此如何实现更高的精度、更好的泛化性、更短的训练时间和测试时间手写体数字识别应用仍是未来值得继续研究的方向。