以“微元法”为例谈基于思想方法的物理延展式教学

徐海菊

(江苏省南通中学,江苏 南通 226001)

环顾当下的高中物理教学,我们相当一部分教师习惯于给学生呈现“成品化”的物理规律和概念,然后给学生提供相应的例题、习题,让学生在记、背、用的过程中记住概念和公式．笔者认为这样的教学缺失了物理思想方法的浸润，不利于学生物理学科核心素养的发展．在发展学生物理学科核心素养素的大背景下,我们的物理教学应该以物理思想方法作为生长点向外延展,促进学生对物理概念、规律的深入理解,促进学生解决物理问题能力的提升,促进学生对物理思想方法本身的内化．本文以“微元法”为例就如何基于物理思想方法进行高中物理延展式教学谈几点笔者的思考．

1 基于“微元法”,推导物理公式

“公式”是高中物理概念、规律的重要表征方式之一,而公式是如何得到的呢?公式的推导不仅联系着学生前后学习的物理概念,还涉及到物理思想方法的应用,基于物理思想方法的公式推导更能彰显学物理人的智慧．例如,向心加速度的公式是教学的重点,其推导在高中物理教学过程中是难点问题,包含大小、方向2个方面,我们不能仅仅灌输给学生公式,下面以推导“向心加速度”为例,两种方法均蕴含着微元和极限的思想．

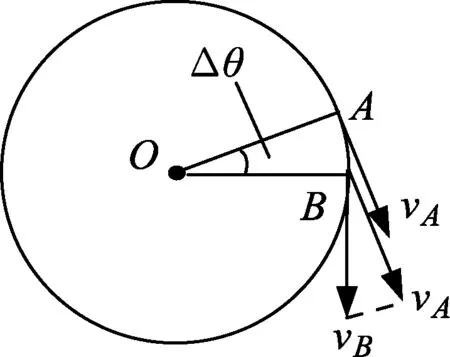
图1

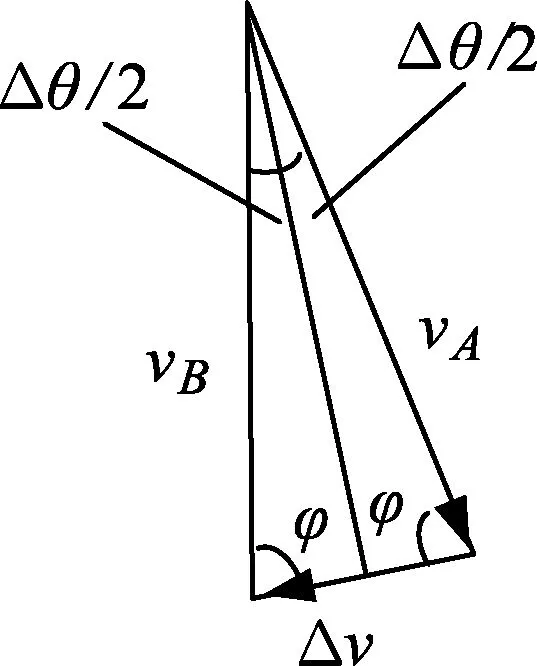
图2

图3

推导2:利用匀变速直线运动规律推导向心加速度公式,匀速圆周运动可以看作是一个沿切向的匀速直线运动和一个沿法向(指向圆心)的匀加速直线运动的合运动,如图3所示．设质点以速率v沿半径为R的圆做圆周运动在时间t内从A点运动到B点．连接OB并延长与过A点的切线交于C点．

(1)

沿法线方向有

(2)

由勾股定理有

(3)

(4)

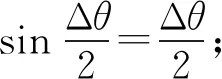
2 基于“微元法”,理解规律外延

“文字”是高中物理教材中对物理概念、规律又一种重要表征方式,有些概念、规律除了文字表征外还配上了图像、公式,学生要充分理解和内化物理概念、规律就必须深入到规律的内涵与外延学习中去,而学习的过程又不可缺失了物理思想方法的渗透．下面以开普勒第二定律为例．

人教版必修2教材中,开普勒第二定律的文字表征为:“对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积．”

图4

配合图4所示的行星运动简图,根据开普勒第二定律,学生很容易理解在靠近太阳的地方(近日点),行星运动的弧长较长,在离太远较远的地方(远日点),行星运动的弧长较短,继而得出次级规律:对任意一个行星来说,近日点运动得快,远日点运动得慢．在得到这个次级规律时,其实就用到了微元、比较的思想,但是还不够明显,为了让学生深刻认识到开普勒第二定律的外延,我们可以设置如下问题,让学生进行思考,在解决问题的过程中完成对规律深度学习．

问题1.如图4所示,某行星围绕太阳C沿椭圆轨道运行,它的近日点A离太阳的距离为a,行星经过近日点A时的速度为vA,行星的远日点B离开太阳的距离为b,求它经过远日点B时速度vB的大小．

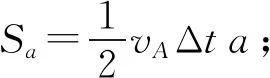
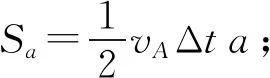
3 基于“微元法”,破解原始问题

物理源于生活，在生活中有很多值得我们思考的原始物理问题,笔者在和学生一起学习动量、冲量时,课后就有学生想着去“称冲击力”,大多数学生是将物块放在台秤上称其重力,然后在一定高度释放,观察撞击台秤时台秤示数变化．但是有一组学生是用一根链子做的实验,观测到了示数连续的变化,于是他们咨询其中的“奥秘”,当时笔者就意识到这是一个很好的“探究资源”,于是笔者就带了一个台秤、一条链子,在课堂上进行了演示实验,然后抛出一个与之相关的物理问题．

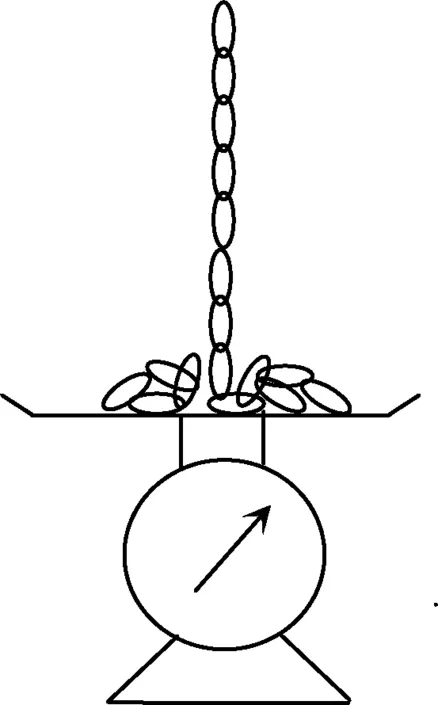
图5

问题2.如图5所示,质量为M、长度为L的链子,铅直地悬挂在磅秤的上方,下端恰好触及秤盘．放开链子,使其落在秤盘上．当链子中长度为X的一段已经落下时,磅秤的读数是多少?

应用微元法分析:由于各段链子从不同高度落下,落至秤盘的速度并不相同(越来越快),对桌面的冲击力越来越大．设开始下落的时刻为t=0,经时间t,链子落秤盘上的长度为X,此时链子的下落速度为v,已知链子的线密度为

(1)

从t时刻再取一段很短的时间Δt,在Δt时间内链子下落ΔX长度,其质量为

ΔM=ρΔX.

(2)

落到秤盘上后,链子的速度变为0,由运动学规律可得,链子下落到秤盘时的速度为

v2=2gX.

(3)

当微元质量ΔM冲击秤盘时,秤盘对ΔM的反作用力为F′,对ΔM应用动量定理有

F′Δt=0-ΔMv.

(4)

则磅秤的读数为

N=ρgX+F.

(5)

且有

F=F′.

(6)

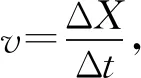
“微元法”是高中物理常用的辅助解题方法,通常是取物体运动过程中微小的一段运动,可以与一系列物理量相对应,如时间Δt、长度Δx、角度Δθ、质量Δm、……．微元法分析、解决问题的过程都可能与极限、导数或微分有着紧密的联系,或者直接运用极限、导数或微分分析计算,其实不管是哪一种思想方法,我们如果仅仅将其定位在解题方法与手段上,显然是狭隘的,应该在整个高中物理概念、规律教学和问题解决过程中都应该渗透与应用,只有这样才能让学生全方位感受到物理的魅力,而不是物理题难．