江苏省县域经济TFP增长率的分解与估算：2000～2016

马卫东 唐德善

摘要：采用了超越对数生产函数的随机前沿模型测算了江苏省54县区市2000～2016年的全要素生产率增长率并对其结构要素进行分解。研究表明：用两步法探索随机前沿的模型参数，发现增加出口比重、第二产占比、城市化比率和财政支出比率等环节变量后，模型解释力有明显提升62%。出口比重和城市化率对生产效率提升具有明显正向促进作用，二产占比和财政支出占比与生产效率却呈负相关关系。技术进步贡献最大，TFP增长率的变化主要源自于技术进步的推动，对TFP增长率的平均贡献在82%以上，总体上带动TFP呈现缓慢上升趋势。

關键词：全要素生产率;经济增长;分解要素结构;三类聚类地区

近年来，经济增长动力源泉一直是政府部门和学术界普遍关注和研究的热点问题。新古典经济增长理论认为驱动经济增长的主要动力源自要素投入和技术进步（全要素生产率）等因素的共同作用。近期国内主流文献也证实了改革开放以来我国经济增长动力主要源自资本投入驱动，技术进步率贡献较小并呈逐年下降的趋势，形成了现阶段的资本投入与TFP“反向角力态势”。要素规模增长率下降与产出弹性缩减的双重挤压导致了资本与劳动规模贡献下降，资本与劳动的生产率的增长率双减速是造成了全要素生产率的下降的主要原因。在没有提高全要素生产率对经济增长贡献条件下，即使政府能够通过一系列政策和制度的安排以强化资本投入来获得了一定时期内经济较快增长，但是，经济增长动力最终也会由于要素边际产出递减的约束下而衰减。早期关注江苏县域全要素生产率的相关文献非常稀少，研究时段也大多集中在2012年前后。鉴于此，本文以江苏省2000～2016年间54个县市的面板数据，探索江苏省县域经济全要素生产率增长率分解构成及变化趋势。

一、分析框架与方法

（一）研究方法的设计

当前，主流的TFP方法主要有三种：第一种是增长核算法，这种方法主要利用统计数据估算出要素的产出弹性，从而通过生产函数的具体形式测算出TFP，比如索洛余值法。第二种是非参数方法，这种方法适用于面板数据，并可将TFP分解为技术进步、技术效率以及规模效率等不同构成要素，但是这种方法计算的TFP在很大程度上只具有相对意义。第三种是参数法。应用最为广泛的是随机前沿分析方法。这种方法所设定的超越对数生产函数模型不仅放松了索洛余值方法中关于充分竞争、规模效益不变、希克斯中性三大假设，还考虑了随机因素对产出的干扰因素，以及随机前沿生产函数的具体形式可检验性，提高了拟合效果，具有明显的现实意义。考虑到各种研究方法的优缺点和适用性，本文认为采用超越对数生产函数的前沿模型计算得出的TFP比较客观，特别是其放松了常替代弹性这一假设，并且通过一系列检验能够验证模型的适用性和具体形式。

（二）生产函数估计与TFP分解

本文对江苏省县域TFP的测算采用随机前沿分析方法（SFA）。文中模型初始形式设定为超越对数生产函数，其具体形式如式1所示：

lnYit=β0+βKlnKit+βLlnLit+βtt+1/2βKK（lnKit）2+1/2βLL（lnLit）2+βKL（lnKit）（lnLit）+βKt（lnKit）t+βLt（lnLit）+1/2βitt2+υit-μit（1）

其中，Yit表示i地区t年份经济产出，K、L分别表示资本和劳动力投入量，β为待估参数，η为技术效率时变参数;υit-μit为合成误差项（εit），υit为随机干扰项，衡量系统非效率程度，服从标准正态分布;μit为技术损失误差项，反映了技术无效率程度，服从于零点截断半正态分布。

在估计随机前沿生产函数模型的基础上，本文将参考Kumbhakar（2000）和余永泽（2015）关于 TFP 增长率计算和分解方法，生产函数对时间t求导数，为简单起见，省略下标it则有：

上式中，TF·P表示全要素生产率增长率，T·E为技术效率变化率，TP为技术进步率，SE为规模效率改进，Ej为要素产出弹性，E=∑Ej表示规模弹性。

（三）变量选择与处理

本文以2000～2017年江苏省54个县市域的产出、投入和要素成本为研究样本。为了数据前后统一，以现有县市域区位为单位，兼顾地区名称变换。2017年总产出数据、资本总额和劳动力数量等最新数据来源于2018年度各县区市政府工作报告、统计局公开数据或经本人计算得到结果。

1. 总产出数据（GDP）

数据源于万得金融数据库，部分缺失数据源自2017年江苏省统计年鉴或各县区市统计局公开数据。用地区生产总值（GDP）来衡量总产出，对各县市的GDP按2000年不变价进行了平减处理，用以得到真实产出。

2. 资本总额数据（K）

采用固定资产形成总额进行衡量。以2000年为计量基期，以当年价格计算的固定资本形成总额以及固定资产投资价格指数，年折旧率为10.6%，采用永续盘存法测算各年度江苏各县区市的固定资本存量。

3. 劳动力数据

本文选用t-1年末和t年末“就业人员数”的算术平均值作为t年劳动投入量。

4. 环境变量

借鉴欧向军和牛品一等研究文献，本文选取出口总额占GDP比重（简称“出口占比”，下同）、第二产业占GDP比重（二产占比）、城市化率、政府财政投入占GDP比重（财政投入占比）等因素作为影响技术效率的环境变量，分别采用一步法和两步法探索环境变量对技术效率影响进行测度。

（四）模型检验

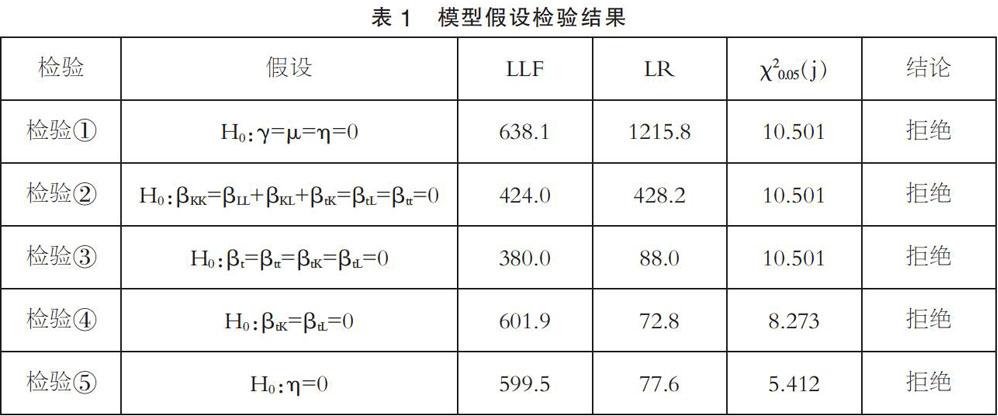
通过使用似然比统计量LR=-[L（H0）-L（H1）]对随机前沿模型适用性等指标进行检验，其中，L（H0）和L（H1）分别为零假设和备选假设对应的对数似然函数值。检验①中，零假设设定为γ=μ=η=0。从表1检验结果显示，远远大于临界值χ20.05（j），所以拒绝了零假设，随机前沿生产模型具有适用性。检验②是对生产函数的具体形式进行检验， LR远大于临界值，所以拒绝了零假设，模型适用于采用超越对数的随机前沿生产函数形式。检验③进一步检验模型是否存在技术变化，此时零假设H0，备择假设H1，似然比检验统计量LR大于临界值，所以拒绝零假设，认为模型存在技术变化。检验④检测了模型技术变化是否为希克斯中性，零假设H0，备选假设H1，似然比检验统计量LR大于临界值，拒绝零假设，认为模型技术变化没有表现为希克斯中性，技术变化与资本和劳动等投入要素有关。最后，检验⑤检测了技术效率是否具有时间变化特征，结果显示，拒绝原假设H0，接受备选假设H1，认为技术效率模型具有随时间变化特征。