基于基本解方法的有限平面Darcy渗流的研究
陈润波 凌小双
南通大学 交通与土木工程学院 江苏 南通 226019
1 引言
渗流在水利、地质、采矿、环境保护、化工、生物、医疗等领域都有广泛的应用。在渗流研究中,杨和刘等人介绍了渗流理论在导电复合材料机理研究中的应用和最新进展;朱和祝利用渗流理论设计方案提高了采油效率。
本文利用基本解方法对有限区域中存在汇点的土石坝渗流问题进行了计算,推动了无网格计算在Darcy渗流复杂边界值问题中的应用。
2 基本方程
2.1 Darcy渗流基本方程

当材料为各向同性时,稳定渗流的微分方程式为拉普拉斯方程
式中,h为测压管水头,上式只包括一个关于测压管水头的未知函数,在理论上结合边界条件就有定解。
2.3 MFS方法
由于各向同性渗流控制方程为拉普拉斯方程,二维拉普拉斯方程的方程可表示为如下的形式:
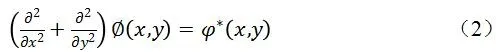
式中为研究区域中的未知函数,为区域中的已知函数,在区域的边界上,在本文中,只简单的给出了两类边界条件典型形式(即Dirichlet , Neumann两种边界条件)

式中n为边界上的外法线方向余弦。
根据基本解方法思路,在区域的外部且靠近边界外取虚边界,并把点取在虚边界上,用表示。函数可表示为
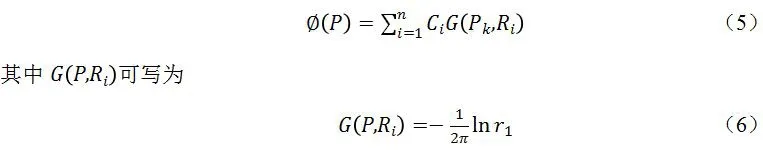

如果满足Neumann边界条件时,根据式(4),式(5)中的待定系数可由如下形式的线性方程求出
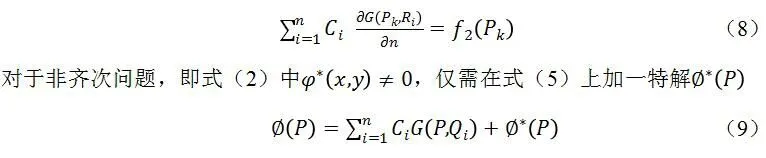
Dirichlet边界条件
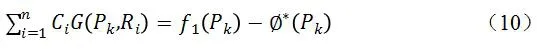
Neumann边界条件
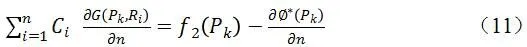
3 数值计算结果
如图1(a)、(b)所示,设存在一个无限长的粘土坝体,渗流系数K=15.20*10^-10m/s。坝长远大于坝宽和坝高,坝体左侧存在与坝体等高的水位,大坝尺寸为矩形区域,坝内在处存在一个汇点,此问题可以简化为平面问题。
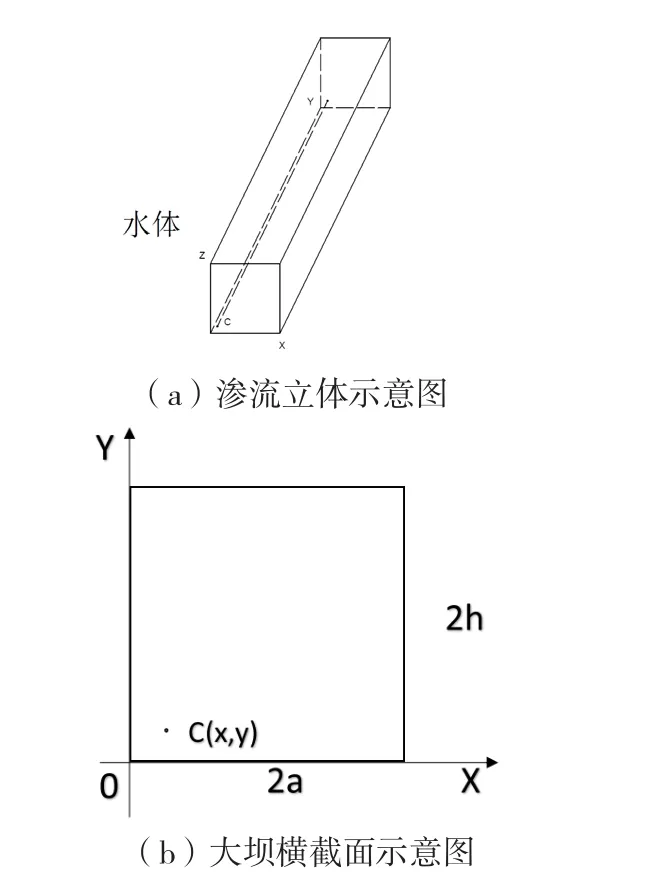
图1 大坝渗流示意图
对于存在汇点的渗流,汇点特解为如下形式
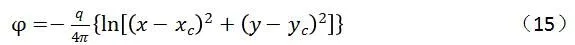
式中,q为汇点强度,且q=-10^(-8)/k。
利用基本解方法对上述问题进行计算,势能水头都是单调递增的,而在点(5.45,5)处发生了转折,这与汇点布置状况是相符的。且水流流速均为负值,这表明水流流速整体方向向下,另外流速均为两边大,中间小,而这与实际工程状况相符,是由左边界的水流压力作用和右边界的自由条件引起的。
4 结语
主要对土石坝渗流的情况进行了模拟计算,得到相对精确的数值解,渗流流线趋势及势能水头变化规律都符合预期,验证了重构基本解函数的正确性,证明了基本解方法在渗流计算中的可行性。

