埋深对盾构超挖地表沉降影响的模型试验

黄赵美 ，曹广勇 ，李秉坤 ，马海军

(1.安徽建筑大学 土木工程学院，安徽 合肥230601；2.安徽建筑大学 建筑结构与地下工程安徽省重点实验室，安徽 合肥 230601)

0 引言

盾构施工作为目前城市轨道交通建设最主要的一种施工方法，有工期短和交通影响小的优点[1-2]，其弊端是盾构机超挖导致土体损失，引发地表沉降，且地表沉降值[3]是盾构法施工的安全控制指标之一。为探究盾构超挖对地表沉降的变化规律[4-8]，首先采用石英砂模拟盾构超挖对地表沉降规律的研究，主要因为砂土环境中盾构隧道施工的理论和模型试验有较多的资料查阅。魏纲[9]通过假设两圆相切的土体损失模型，通过设立移动焦点参数和坐标系，建立了包括了park模型和Loganathan模型在内的统一土体移动模型，郑刚[10-11]基于室内模型实验分别研究了砂土超和补偿的的隆沉曲线变化规律；针对黄土和软土等特殊土质的盾构超挖引起地表沉降方面有较多的工程项目监测数据[12-13]，盾构施工技术应用较为成熟。但是在盾构室内模型试验方面的研究相对较少，从模型试验方面探究盾构施工隧道埋深位置、土体超挖量与地表沉降之间的关系，对改善盾构施工方法有理论意义。

1 试验设备

本实验采用自行设计的室内模型实验平台，通过控制隧道管和橡胶模间的水量，可以获得不同埋深位置和不同土体损失率情况下隧道中心点地表沉降值实验数据。

本实验的设备主要有砂土实验箱系统，二维模型隧道，激光监测数据采集系统和注排水系统。

1.1 砂土实验箱系统

砂箱实物如图1所示，砂箱尺寸为1.5 m×0.8 m×0.7 m，用砂量约为0.72 m3，砂箱尺寸是根据peck公式对砂土地表沉降槽形状预测范围制定的，使砂土地表沉降在激光监测系统范围内。砂箱两面为有刻度的透明玻璃，便于观察砂土平面高度。

1.2 二维模型隧道和注排水系统

二维模型隧道如图2和图3所示，由聚氯乙烯材料制成硬质空心管(长350 mm，直径100 mm)，模型隧道直径依据盾构机按1:60比例设计。表面刻宽3 mm、高3 mm的v形螺旋刻槽和平行于隧道方向宽4 mm、高3 mm的直角u型的刻槽，主要作用起到注水和排水的畅通性，保证实验在较大埋深的情况下能够顺利模拟实验；两端则各有一注排水孔。通过控制一端注排水的体积模拟盾构施工过程中注浆补偿量和超挖土体量。

1.3 激光监测数据采集系统

数据采集设备采用型号HG-C1000微型激光位移传感器，其量程范围在100 mm±35 mm内，重复精度在70 μm。激光位移器位置如图4所示。

图1 砂箱实物图

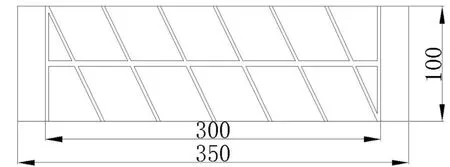
图2 隧道模型示意图(单位mm)

图3 隧道模型实物图

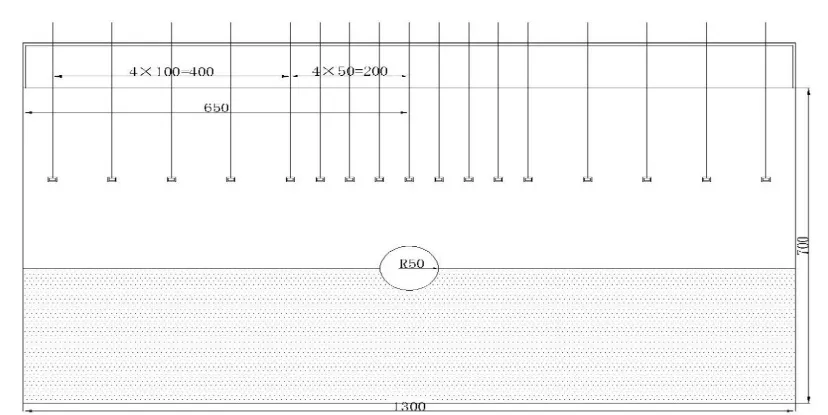
图4 砂土试验箱及激光位移器布置示意图(单位mm)

2 实验概述

模型实验共进行三次，隧道模型埋深位置分别为1D(D表示隧道模型的直径，D=100 mm)、2D和3D。

2.1 砂土、隧道铺设及激光位置设置

砂箱填铺，将砂在10 cm高度均匀填入箱内，每填筑10 cm，平整一次砂平面；填筑至隧道平面，将隧道放到设计位置，再填入砂土直至设计高度。激光位移计采用对称布置，共计17个。隧道中心到左右20 cm范围每间隔5 cm设置一个激光位移计，紧接向外每隔10 cm设置一个激光位移计，砂平面监测范围为120 cm。

2.2 试验数据采集

将隧道管与膜之间注入12%隧道模型体积的水，静置24 h，再次整平砂平面，进行超挖数据采集。一次排出2%的隧道体积的水(47.1 ml)表示本次模拟实际超挖土体2%的隧道模型体积，亦是后面所提到的土体损失率，排水5分钟后，记录砂平面的数据，累计六次排水和六次记录砂平面数据依次进行，可以获得土体超挖分别为2%、4%、6%、8%、10%和12%的六组实验数据。三次试验共计可以获得18组实验数据。

3 试验数据分析

3.1 地表中心沉降规律分析

地表中心点沉降数据如表1所示，并对数据进行二次曲线拟合，拟合的二次曲线方程及相关度如公式(1)所示。

从表1、公式(1)和图5可以得到一下结论:

(1)相同土体损失率，中心点沉降值随着埋深位置的增大而减小；在最大土体损失率为12%情况下，随着隧道管埋深位置从1D至3D，隧道正上方地表中心点沉降值从5.86 mm降低至3.55 mm；

(2)Δ1-2(表示同一土体损失率下埋深1D的地表中心点沉降绝对值与埋深2D的地表中心点沉降绝对值的差值)大于Δ2-3(表示同一土体损失率下埋深2D的地表中心点沉降绝对值与埋深3D的地表中心点沉降绝对值的差值)；从土体损失率2%到12%，Δ1-2值在0.77 mm-1.79 mm范围内；从土体损失率2%到12%，，Δ2-3在-0.04 mm-0.76 mm并逐渐增加，且Δ2-3在土体损失率4%以内很小。

(3)隧道管同一埋深情况下，地表中心点沉降绝对值随着土体损失率的增加而增加，其数值增大的趋势逐步变缓表示同一埋深位置，x+2%的中心点沉降值与x的中心点沉降值的差值，x取值为2%、4%、6%、8%和10%；在1D埋深位置下的值在1.33 mm-0.54 mm范围内，基本满足逐渐减小的趋势；在2D埋深位置下，的值从0.88 mm减小至0.26 mm；在3D埋深位置下的值在1 mm-0.03 mm范围内，基本呈现减小趋势；

(4)1D、2D和3D埋深中心点沉降值实测数据的二次曲线拟合方程和相关度如公式(1)所示，可以表述出砂土损失率和地表中心点沉降值的关系，且三个拟合方程的相对应位置的系数在数值和符号具有较高相似性；

针对上面的结论分析，埋深与中心点沉降值的反向关系，主要是因为土体损失相同情况下，埋深较浅的沉降槽宽度系数小，导致中心点沉降值反而大；中心点沉降值随土体损失率的增加而增大且趋势变缓，主要是因为沉降槽宽度由窄变宽，对沉降槽的竖向的影响效果减弱。

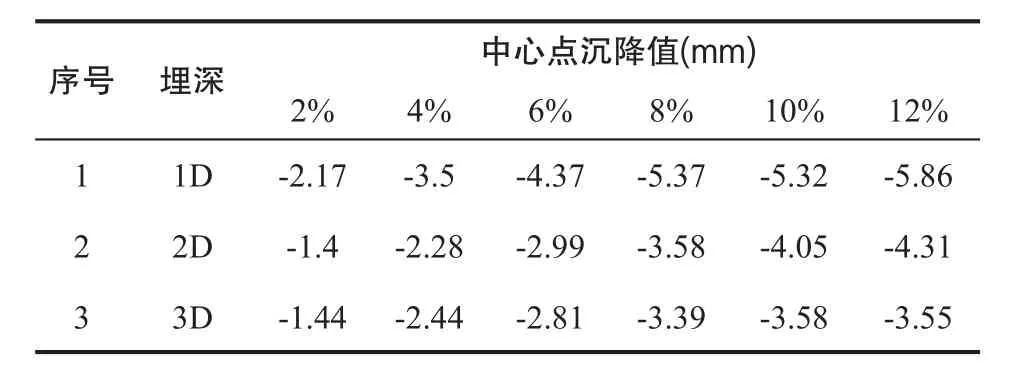
表1 不同埋深地表中心点沉降值

y表示沉降值，R表示二次曲线拟合的相关度，下标1、2、3表示隧道模型的埋深位置。

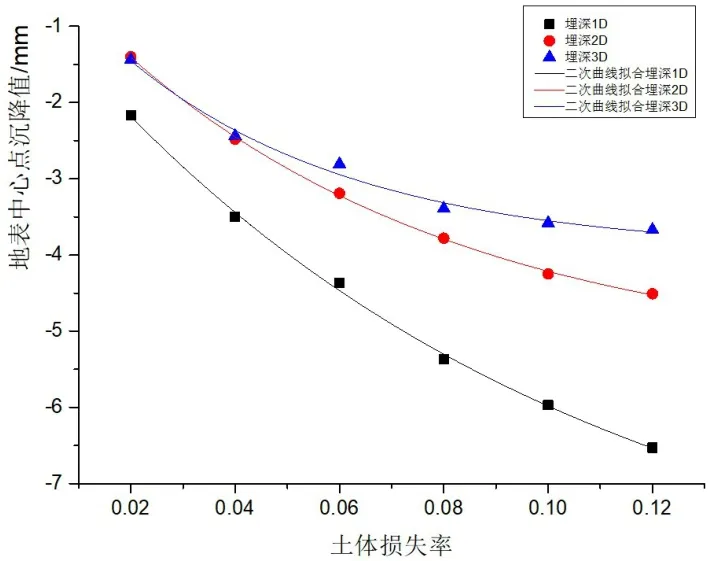
图5 土体损失率和地表中心点沉降值得拟合曲线

3.2 地表沉降范围规律分析

图6是隧道管埋深分别为1D、2D和3D的不同土体损失率的地表沉降值的Gauss曲线拟合。

图6 埋深1D、2D和3D地表沉降曲线图

从图6Guass拟合拟合曲线可以直接看出，随着埋深1D增加至3D地表沉降曲线的沉降槽宽度系数逐渐增大，模型隧道超挖的影响范围主要集中在隧道中心2D-4D位置范围内，沉降槽宽度系数大约从20 cm增加到40 cm；随着土体损失率的增加，沉降槽宽度系数有窄变宽并趋于稳定。这种现象的原因主要是砂土层扰动和砂土损失自下向上传递过程的作用造成。

4 结论与建议

本文通过砂土室内模型实验探究不同埋深情况下盾构超挖对地表沉降的变化规律，得到如下结论和建议。

(1)本文通过试验数据分别拟合得到1D、2D和3D位置的地表中心点沉降值与土体损失率的二次关系曲线，可以表述出土体损失率和地表中心点沉降值的关系；

(2)随着埋深的增加地表中心点沉降值变小，地表中心点沉降值减小的速率变小；随着埋深和土体损失率的增加，沉降曲线的沉降槽宽度系数变大并趋于稳定；

(3)本实验仅做了盾构隧道的超挖一方面，应完善注浆补偿室内模型实验，以方便将超挖和注浆补偿进行对比，得到更为直接全面的认识；

(4)本实验仅做了砂土的模型试验，并没有结合工程进行相似理论计算，应进一步完善室内模型实验，使实验结论对指导盾构施工更具有借鉴价值。