盾构隧道下穿施工对城市下立交的影响分析

王晓煜，刘磊磊

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.上海市隧道工程轨道交通设计研究院，上海 200235)

0 引言

随着盾构施工技术的不断发展，双管盾构在地铁施工中已得到广泛的应用。由于城市建设的飞速发展，轨道交通线路选择受到一定的制约，不可避免的需要横穿建筑物、管线、下立交、高架桥等建构筑物，导致建筑物开裂、倒塌以及管线断裂破损等。因此研究地铁区间隧道施工对建(构)筑物影响具有十分重要的意义。有关盾构隧道施工对邻近建(构)筑物的研究已引起国内外学者越来越多的重视。在理论公式方面，Peck公式仍是应用最多、范围最广的[1]。Attewell等(1982)提出了地表纵向沉降经验公式[2]。刘建航等(1981)提出了地表横向沉降经验公式[3]。在数值模拟方面，陈书文采用有限元数值模拟的方法，研究了盾构隧道侧穿建筑物桩基时，在有无隔离桩的条件下，对桩基的变形和内力的影响[4]。傅雅莉采用FLAC3D分析了地层沉降、桥梁结构变形及桥梁墩台基础的沉降，预测了盾构隧道施工对桥梁的影响[5]。吴瑞等基于合肥地铁2号线下穿五里墩立交桥研究分析了双线隧道开挖中，掌子面滞后0～60 m内，对桩基的横向变形影响不大[6]。王晓睿利用FLAC3D建立数值模型，对盾构施工时对土体的扰动及对已建污水管的施工影响进行了分析[7]。朱玉龙运用MⅠDAS GTS NX软件模拟了盾构侧穿桥梁全过程，得出了在盾构机侧穿桩基时，桩基顶端朝向隧道，底端背离隧道倾斜[8]。在模拟试验方面，藏宏阳、王非通过室内大型模拟试验模拟了盾构隧道下穿时对地层沉降的影响[9]。朱训国、陈枫以大连市地铁2号线为研究对象，通过室内相似材料模型试验，得到隧道施工时引地层的移动规律并得出隧道开挖时若存在地下结构或管线，其将受到附加剪切作用，易出现裂缝，在施工中必须做好切实可行的防护措施[10]。

本文以合肥轨道交通某区间下穿城市下立交为例，通过建立三维有限元地层结构模型对区间隧道下穿城市下立交进行数值模拟分析，对地表沉降及最大差异沉降进行了预测。

1 工程概述

1.1 工程概况

该城市下立交建于2008年，支护体系为排桩，桩径1.2 m，桩长12 m，桩底标高为-2 m，位于强风化泥质砂岩层，底板标高为4.55 m。合肥轨道交通某区间下穿某城市下立交，隧道埋深约为18 m，位于中风化泥质砂岩层，隧道顶距离某城市下立交排桩底部约为3.0 m。盾构隧道下穿下立交剖面示意图如图1所示。

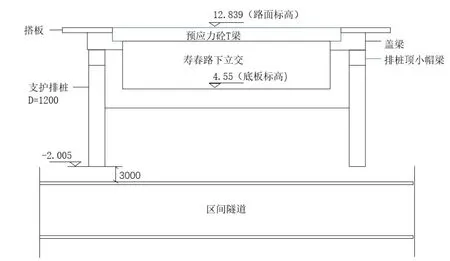
图1 盾构隧道下穿下立交剖面示意图

1.2 地质条件

该区间隧道下穿下立交范围内，土层至上而下分别为杂填土、粉质粘土、粉砂夹粉质粘土、强风化泥质砂岩以及中风化泥质砂岩。区间隧道主要穿越中风化泥质砂岩，隧道顶部为强风化泥质砂岩。

根据地质勘察报告，杂填土中主要以上层滞水为主，水量微弱。承压水主要赋存于层粉砂夹粉质黏土中。由于拟建场地承压含水层基本位于拟建区间顶板以上，对拟建区间影响不大。基岩裂隙水主要赋存于岩石强、中风化带中。

2 区间隧道下穿下立交数值模拟分析

由于岩土材料物理力学特性的随机性和复杂性，完全模拟岩土材料的力学性能和严格按照实际的施工步骤进行数值模拟是非常困难的。因此，在本模型建模过程中，对实际开挖步做了适当的简化和合理的假设:

(1)围岩材料假定为理想弹塑性体，并认为地表和内部为均一地层，不考虑围岩中的节理、裂隙等不均匀因素，采用实体单元来模拟，屈服准则采用D-P准则；

(2)隧道管片采用板单元来模拟，并且按照线弹性来计算，不考虑其非线性；

(3)假定围岩中不存在构造应力或构造应力很小可以忽略，所以在模型中只考虑围岩自重应力；

(4)简化地表和各土层使其呈均匀的水平层状分布。

(5)桩基采用桩单元进行模拟，均不考虑其非线性。

2.1 有限元模型的建立

该项目采用MⅠDAS GTS NX进行建模。通过对地层的简化和假设，取计算模型长66 m，宽66 m，高33 m。设定边界条件时，将模型底部边界条件设为x，y，z方向约束，即固定边界，将模型两侧边界条件设为x或y方向的水平约束，即水平边界。模型中的各种材料的力学参数见表1、表2。土层采用实体单元，管片采用板单元，桩基结构采用桩单元。管片视作弹性体，土体采用莫尔库伦模型。网格划分采用混合网格生成器。通过钝化与激活单元来模拟隧道的开挖与支护，模拟隧道开挖时，将所需开挖的土体单元钝化，施加管片进行支护模拟时，将预先设置好的管片单元进行激活。所建立的整体有限元模型和桩基有限元模型见图2、图3。盾构隧道与下立交的空间关系见图4。

表1 桥梁基础结构参数

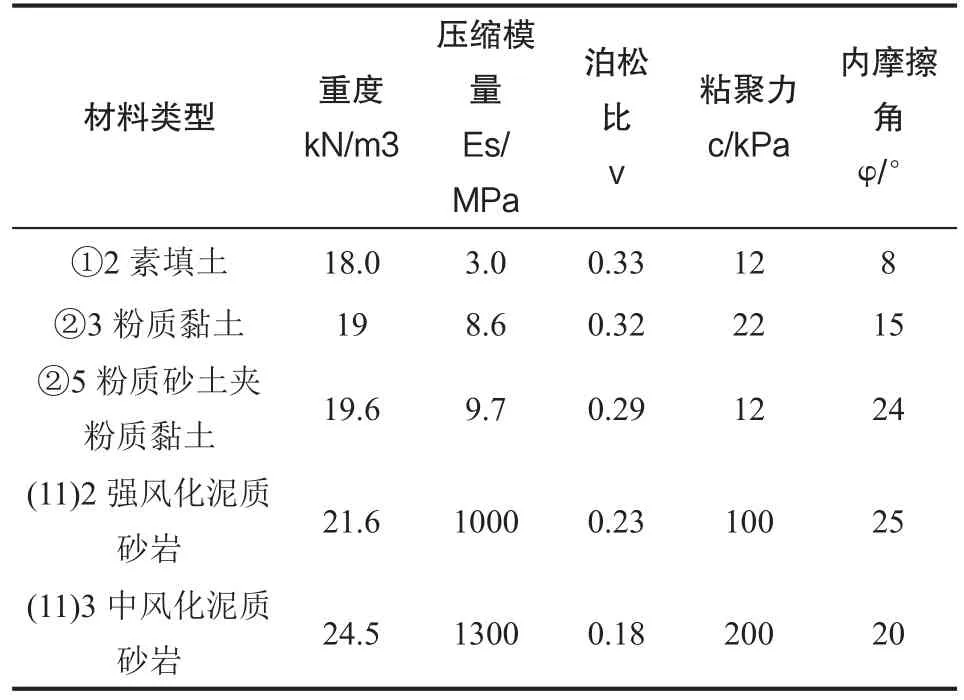
表2 地层力学性质参数

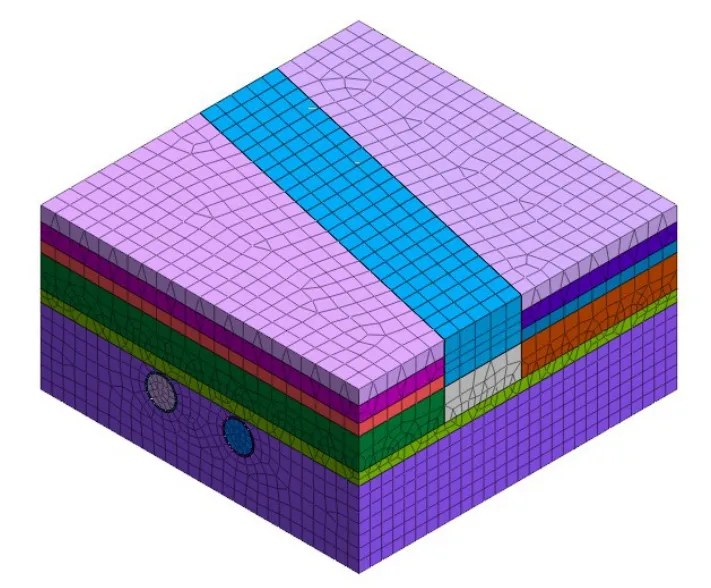
图2 整体有限元模型

图3 下立交有限元模型图

图4 下立交与隧道相对位置关系图

2.2 计算说明及步骤

盾构隧道在下穿城市下立交的施工过程中，注浆效果、掌子面顶推力、盾构掘进速度等一系列反映盾构施工控制水平的因素都会对地层、城市下立交产生影响，不同的施工控制水平产生的影响是不同的。在数值计算中考虑施工控制水平的方法通常有释放应力法，等代层法等，本项目采用等代层法。模拟开挖步骤为:施加重力、计算土体及下立交初始地应力场、位移清零、隧道分步开挖计算，每6m为一个施工步，每个阶段包括开挖和支护两个施工步序，总共22个施工阶段、计算结果分析。

2.3 计算结果分析

2.3.1 隧道开挖引起的土层沉降情况分析

(1)左线开挖后地层沉降分析

图5为左线开挖后地表沉降云图，图6为左线开挖后地层沉降云图。

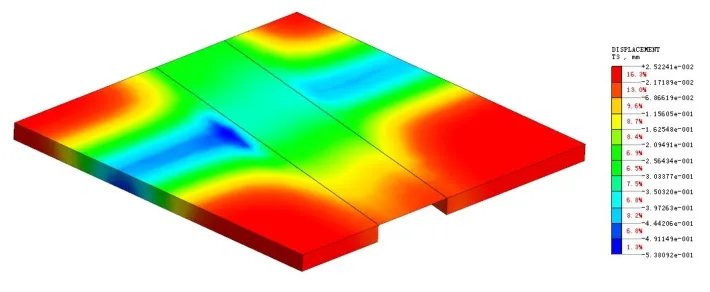
图5 左线开挖后地表沉降云图

图6 左线开挖后地层沉降云图

由图5～图6可知:由于左线隧道开挖，地层产生明显的沉降槽；地表沉降计算值最大为0.5 mm，隧道拱顶最大沉降为1.7 mm。

(2)双线开挖后地层沉降分析

图7为双线开挖后地表沉降云图，图8为双线开挖后地层沉降云图。

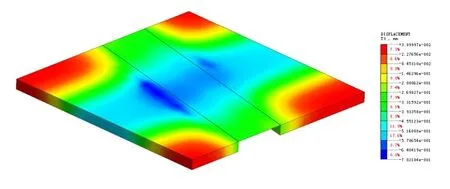
图7 双线开挖后地表沉降云图

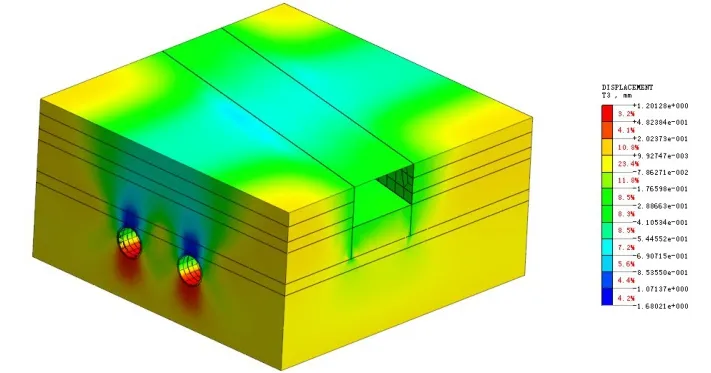
图8 双线开挖后地层沉降云图

由图7～图8可知:由于隧道开挖，地层产生明显的沉降槽；地表沉降计算值最大为0.7 mm，隧道拱顶最大沉降为1.7 mm。

2.3.2 隧道开挖引起的下立交沉降情况分析

(1)下立交沿道路方向的差异沉降分析

图9、图10分别为左线及双线开挖后下立交沉降云图。

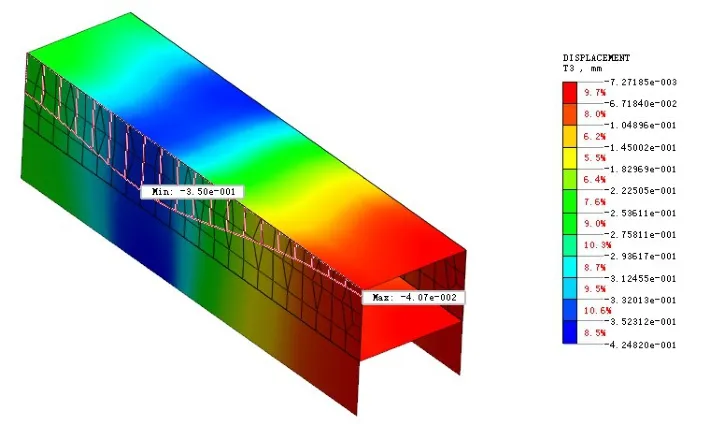
图9 左线开挖后下立交沉降云图

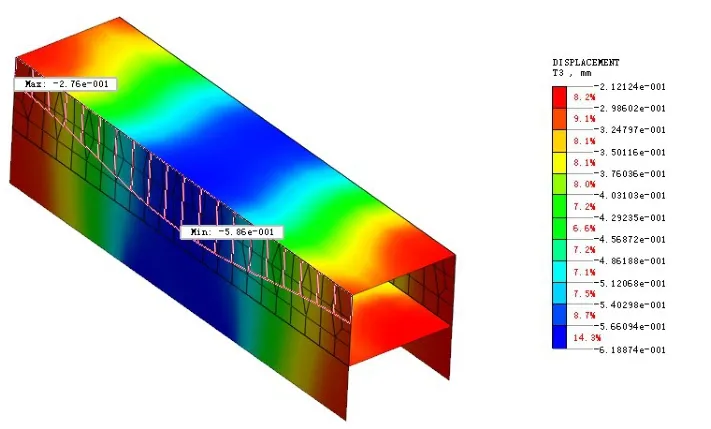
图10 双线开挖后下立交沉降云图

根据图9、图10可以看出，左线开挖后下立交的最大沉降为0.35 mm，最小沉降为0.04 mm，差异沉降为0.31 mm，差异沉降率约为0.31 mm/48 m=0.006‰；双线开挖后下立交的最大沉降为0.59 mm，最小沉降为0.28 mm，差异沉降值为0.31 mm，差异沉降率约为 0.31 mm/33 m=0.009‰。

由以上可知，双线开挖过程中，下立交沿道路方向的最大差异沉降率为0.009‰，发生在左线开挖完成时，未超出《公路桥涵地基与基础设计规范》(JTG D63-2007)关于倾斜的限值(2‰)。

(2)下立交垂直于道路方向的差异沉降分析

图11、图12分别为左线及双线开挖后下立交沉降云图。

图11 左线开挖至下立交中部时下立交沉降云图

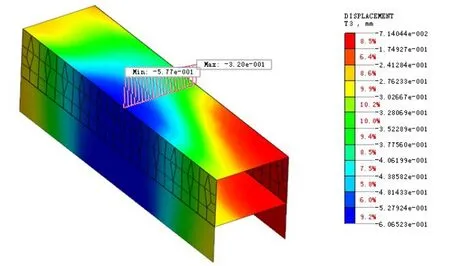
图12 双线开挖至下立交中部时下立交沉降云图

根据图11、图12可以看出，左线开挖后下立交中部时的最大沉降为0.26 mm，最小沉降为0.01 mm，差异沉降为0.25 mm，差异沉降率约为0.25 mm/18 m=0.014‰；双线开挖后下立交的最大沉降为0.58 mm，最小沉降为0.32 mm，差异沉降值为0.26 mm，差异沉降率约为0.26 mm/18 m=0.014‰。

由以上可知，双线开挖过程中，下立交垂直道路方向的最大差异沉降率为0.014‰，发生在双线开挖完成时，未超出《公路桥涵地基与基础设计规范》(JTG D63-2007)关于倾斜的限值(2‰)。

3 监测变形分析

盾构隧道左线2017.5.3～2017.5.10顺利穿越下立交，右线于2017.6.26～2017.7.5再次顺利穿越。根据监测数据显示，左线穿越后下立交的累计最大沉降0.25 mm，右线穿越后下立交的累计最大沉降0.48 mm。在盾构机穿越过程中，对地表沉降、拱顶沉降、周边收敛进行了专项监测。依据监测情况及时修正调整盾构机的掘进参数，进一步保证了穿越过程中下立交的安全。监测数据统计见图13、14所示。

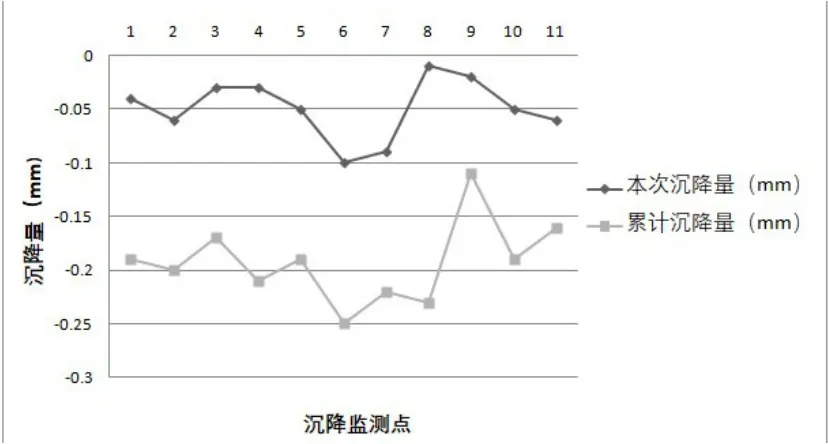
图13 2017年5月10日左线盾构穿越立交桥沉降情况统计

图14 2017年7月5日右线盾构穿越立交桥沉降情况统计

4 结论

本文利用MⅠDASGTS NX建立数值模型，对盾构下穿城市下立交的地铁盾构施工进行安全风险分析，并通过分析结果对施工进行指导和建议。

(1)通过数值模拟计算和分析表明，现阶段该城市下立交可满足正常使用，地铁穿越施工引起的下立交差异沉降未超过差异剩余变形量，构筑物可不拆除。

(2)下立交双线贯通后，根据监测结果表示，下立交最大累计沉降量为0.48 mm，满足沉降控制标准。沉降模拟结果与监测结果比较分析，误差为17.2%，模拟结果较为可信，表明MⅠDAS能较好的模拟盾构隧道三维动态开挖过程，可为类似工程提供参考。