基于SPSS数据分析中国主要省市的农林牧副渔业产值大小

张怡

摘  要： 本文主要运用了2013年我国31个主要城市的农林牧副渔业的各产值155个样本横截面数据，本次采用技术路线是用聚类分析将全国31个省份农林牧副渔业发展相似的个体归为一类;其次运用主成分分析来判断在这些城市中农林牧副渔业这五个因素利用聚分析方法将性质相似的个体归为一类;然后用主成分析方法，借助统计软件SPSS，提取出对各省市经济发展影响的主要因素，然后构造主要因素与可控因素之间的线性方程及综合得分函数[1]，通过Excel计算出各个因素的综合得分，对统计结果做出合理解释并进行相关总结。

关键词： 农林牧副渔业;聚类分析;农业发展;主成分分析

中图分类号： S-01    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.01.034

【Abstract】： This paper mainly uses the cross-sectional data of 155 samples of the output value of agriculture， forestry， animal husbandry and fishery in 31 major cities of China in 2013. This technical route adopts the cluster analysis to compare the individuals Followed by the use of principal component analysis to determine these five factors in the city of agriculture， forestry， animal husbandry， fishery， animal husbandry， fisheries， animal husbandry and fisheries by using the method of poly-analysis of similar nature of individuals classified as a category; Then the main factors that affect the economic development of provinces and cities are constructed. Then， the linear equation and comprehensive score function between the main factors and controllable factors are constructed. The comprehensive scores of each factor are calculated by Excel. The statistical results are reasonably explained and summarized.

【Key words】： Agriculture， forestry; Animal husbandry and fishery; Cluster analysis; Agricultural development; Principal component analysis

0  引言

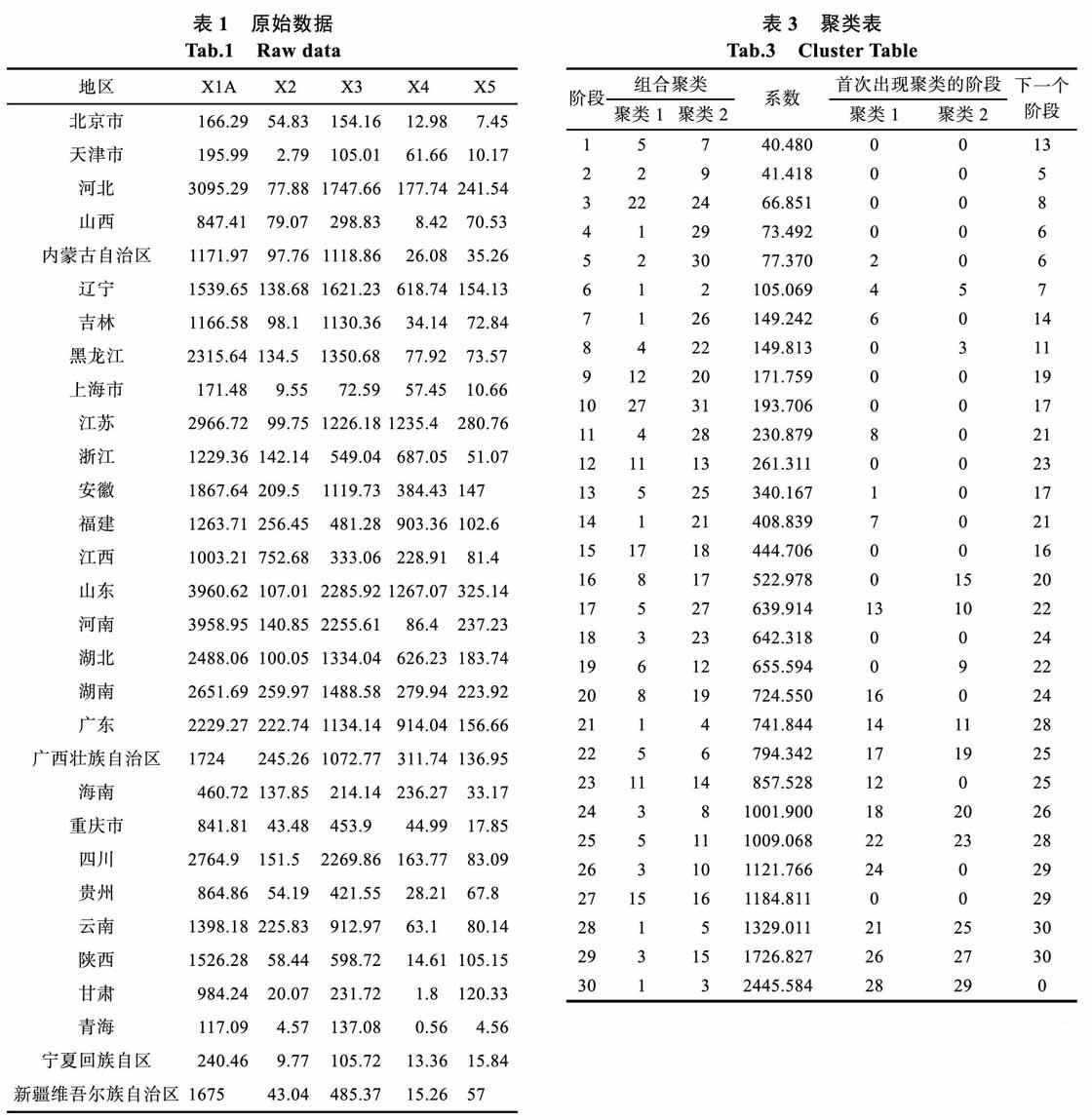
由于農业受自然条件影响较大，有明显的区域性和季节性。我国土地面积辽阔，气候具有多样性导致农业的生产也出现了多样性[2-3]。所以认识到通过适当调整自然资源来促进农业可持续发展的重要性和紧迫性。本文采用2013年的全国31个省份农林牧副渔业相关数据，同时结合国家统计局部分权威指标，归纳指标如下：X1：农业总产值（亿元）、

X2：林业总产值（亿元）、X3：牧业总产值（亿元）、X4： 渔业总产值（亿元）、X5：副业（农林牧渔服务业总产值）总产值（亿元）这五个方面。

3.2.2  结果分析

由谱系图结果可以将我国31个省、市、自治区根据农林牧副渔产值作如下分类。

第一类：山东省、河南省;

第二类：河北省、四川省、黑龙江省、湖北省、湖南省、江苏省、广东省;

第三类：重庆市、贵州省、山西省、甘肃省、北京市、青海省、天津市、上海市、宁复回族自治区、西藏自治区、海南省、;

第四类：内蒙古自治区、吉林省、云南省、陕西省、新疆维吾尔自治区、安徽省、广西壮族自治

3.3  K-均值

3.3.1  K-均值聚类

如表4所示。

3.3.2  结果分析

第一类：山东省、河南省;

第二类：河北、辽宁、黑龙江、江苏、安徽、湖北、湖南、广东、四川;

第三类：北京市、天津市、山西、上海市、海南、重庆市、贵州、西藏自治区、甘肃、青海、宁夏回族自治区;

第四类：内蒙古自治区吉林、浙江、福建、江西、广西壮族自治区、云南、陕西、新疆维吾尔族自治区;

3.4  判别分析得出结果

判别分析是合适的统计分析方法，判别分析最基本的要求是：分组类型在两组以上;每组案例的规模必须至少在一个以上。

表5结果显示，通过初始判别预测，1组2个全部判对，2组7个全部判对，3组11个全部判对，4组11个全部判对，从而有100%的原始观测被判对;在交叉验证中，1组2个全部判对，2组6个判对、1个判错给了1，3组11个全部判对、4组11个全部判对，从而有96.8%的原始观测被判对。

反观K-均值分类法，通过初始判别预测，有100%的原始观测被判对;在交叉验证中，有 90.3%的原始观测被判对。故选用系统聚类（组间连接）分类合适。

3.5  主成分分析

3.5.1  数据准备

数据来源于上述表1数据。

3.5.2  主成分分析结果

程序运行结果得到KMO抽样适应性测度值：Kaiser-Meyer-Olkin=0.696，大于0.6，一般认为此值越大，做主成分分析的效果越好。

从表8中可得到只有前两个成分的特征值大于0.9，即是3.185和0.958，所以选取两个作为主成分。根据累积贡献率超过80%的一般选取原则，主成分和主成分的累积贡献率达到了82.849%的水平，表明原来5个变量反映的信息可由这两个主成分反映82.849%。

從表9中可以看出，第一主成分基本支持了X2，X3，X4，X5，而第二主成分仅仅在X1上表示支持。该成分因子对各省的农业发展有预报作用。第一主成分与牧业总产值（亿元）、副业（农林牧渔服务业总产值）总产值（亿元）、农业总产值（亿元）高度正相关，因此第一主成分可以反映影响该省农业发展的农、牧、副动态发展因素，第二主成分与林业总产值（亿元）高度正相关，因此直接反映影响各省农业发展状况的林业静态发展因素。

3.5.3  分析结论

因为本次研究是为了研究各省农业发展的情况，我们可以看到第一主成分基本支持了X2，X3，X4，X5。第二主成分支持了X1，所以计算每个样本在第一主成分和第二主成分方向的得分。

可以对数据进行标准化，并用每个样本乘以第一成分得分矩阵，即得各样本在第一主成分的综合

4  结论

采用统计学相关的分析方法对我国31个省、市、自治区就农林牧副渔业各产值进行具体分析，并将我国31个省、市、自治区进行综合得分排名。其中，得分为正值，表示该城市农业高于平均水平;反之，表示该城市农业发展低于平均水平。在农业总产值（亿元）、林业总产值这两个提取的主成分上得分高于平均水平（即得分大于零）的是由山东、江苏、广东、河南、湖南、江西、湖北、河北、辽宁、福建、安徽、广西、四川、黑龙江组成，代表着2013年农业产值较高，农业发展较好的省份，尤其是山东省，农业总产值居首位;从结果可以看出，农业产值受自然条件及教育科技发展等方面的影响，上海市、天津市、北京市是我国政治、经济文化发展较快的地区，主要以第三产业为主，第一产业产值较低，而西藏自治区、青海省由手自然条件恶劣，生态环境脆弱，导致农业产值较低。在农业产值较高的省份，如山东省、河南省、河北省、四川省等除了自然条件因素较好外，教育与农业技术的发展也为农业的发展创造了较好的条件。

参考文献

何晓群. 多元统计分析[M]. 北京： 中国人民大学出版社， 2011.

赵晓葵. 基于聚类分析的青海藏区社会经济发展水平评价研究[J]. 青海师范大学学报， 2010.

国家统计局《中国统计年鉴-2012年农林牧渔业产值》.

高惠璇编著， 《应用多元统计分析》北京大学出版社， 2005. 1.

何亮. 主成分分析在SPSS中的运用[J].山西农业大学学报， 2007（4）： 44-46.

Abdul-Wahab SA， Bakheit CS， Al-Alawi SM （2005） Principal component and multiple regression analysis in modelling of ground-level ozone and factors affecting its concentrations. Environ Model Softw 20（10）： 1263-1271.

YOSHIOKA Masataka， LIANG Hongbo， UEDA Naoya， IWATA Yu， TIAN Ye， ZHU Chi. Construction of BMI Power Assist System with the EEG-Torque Modele Using Principal Component Analysis[J]. The Proceedings of JSME annual Conference on Robotics and Mechatronics （Robomec）， 2017， 2017（0）.

薛薇. 基于SPSS的数据分析[M]. 北京：中国人民大学出版社， 2006.

唐功爽. 基于SPSS的主成分分析于因子分析的辨析[J]. 统计教育， 2007（2）.

鞠英杰. SPSS统计分析研究的有利工具[J].统计与咨询， 1999（6）： 36.