干气密封摩擦界面法向接触刚度分形模型

孙宝财， 丁雪兴， 陈金林， 张伟政， 严如奇

(1.兰州理工大学 石油化工学院，兰州 730050； 2.甘肃省特种设备检验检测研究院，兰州 730050)

干气密封作为一种先进的旋转轴用动密封，具有性能可靠、使用寿命长、功耗低、维护成本低等优点，而且能够在高温、高压、高速以及各种强腐蚀性介质等苛刻工况下可靠运行[1]，因而已逐步取代其他密封形式，成为石油、化工、冶金等行业高参数旋转机械轴封的主流[2]。近年来，干气密封已被国内外广泛研究。目前，干气密封的研究主要集中在三个大的方面：①干气密封性能参数的计算与测试[3-7]；②基于稳态条件下的槽形结构参数优化[8-10]；③基于结构动力学理论的气膜动态特性分析[11-13]。这些研究对干气密封的发展起到了巨大的推动作用。

理论上讲，干气密封只有在启动、停止阶段两端面才会出现接触摩擦[14]。但是，在实际工程应用过程中，由于加工制造、装配误差和工作环境的影响，干气密封端面在正常的运行阶段也会发生接触摩擦的情况[15]。此时，干气密封端面将处于无任何润滑的干摩擦状态之下。现有研究已经表明，物体结构表面一般都具有一定的粗糙度，故动、静环端面相互接触时，真正的接触只发生在个别粗糙峰(即微凸体)的顶部，接触点呈离散分布状态，而大部分区域都是有间隙的。这就意味着两密封端面处于干摩擦状态时，将会发生微凸体间的随机接触与碰撞，进而引起摩擦振动。与此同时，伴随着密封端面的磨损、噪声、温升等现象。最终，整个密封系统将会在这些因素的累积作用下失稳，直至失效。摩擦振动是机械运动摩擦副在摩擦磨损过程中产生的普遍现象，蕴含着许多反映系统摩擦学特征和摩擦状态的信息[16]。因此，对干气密封进行干摩擦状态下的摩擦振动研究具有至关重要的意义，然而研究摩擦振动的第一步便是建立摩擦界面的接触刚度、接触阻尼等基本物理参量。

国内外学者就法向接触刚度问题已做了许多研究。在理论研究上大都集中于三个方面：①基于统计接触模型的建模研究[17-20]；②基于分形接触理论的建模研究[21-27]；③基于有限元接触模型的数值研究[28-32]。在试验方面研究有二个方面：①利用超声波进行接触刚度的测量[33-34]；②利用接触力、接触位移进行接触刚度的测量，其中对接触位移的测量有多种方法，有图像法[35]、单点激光测振仪[36]、电涡流位移传感器[37]、压电传感器[38]等。纵观以上研究，法向接触刚度的研究都是以微观粗糙表面的接触模型为基础展开的，其中基于分形接触理论的接触刚度模型较基于统计学参数接触理论的接触刚度广泛，主要是因为粗糙表面具有良好的分形行为，并且这一行为与尺度无关，其分形参数可以很好的描述粗糙表面的形貌信息。众多法向接触刚度分形模型[39-40]都是根据M-B分形接触模型[41]或Wang等[42]修正的M-B分形接触模型建立的。然而，这两个模型自身存在一定的不足，对此我们进行了详细分析，并建立了基于基底长度的粗糙表面分形接触模型，具体内容见文献[43]。当前，对干气密封摩擦界面法向接触刚度的研究还未见报道。

本文根据重新建立的微凸体接触变形方式，结合接触力学及概率理论建立干气密封摩擦界面法向接触刚度分形模型，并通过数值分析得到干气密封摩擦界面接触刚度变化规律以及影响因素，为进一步研究密封界面摩擦振动奠定理论基础。

1 干气密封摩擦界面法向接触刚度模型

1.1 摩擦界面单微凸体受力分析

干气密封摩擦副的动环与静环通常采用一硬一软两种材料配对使用，所以将干气密封硬质环与软质环的接触简化为刚性理想光滑平面与粗糙表面的接触。在这里假设粗糙表面是各向同性的，忽略相邻微凸体之间的相互作用、在接触过程中由于弹性接触的强化作用以及材料硬度随表面深度的变化。本文根据文献[43]确立的单微凸体基底长度的概念(它表示在载荷作用下，微凸体根部恰好未受变形影响处所具有的长度)，重新考虑单个微凸体的接触变形，如图1所示，在本文中为简化问题只考虑塑性与弹性这两个状态。

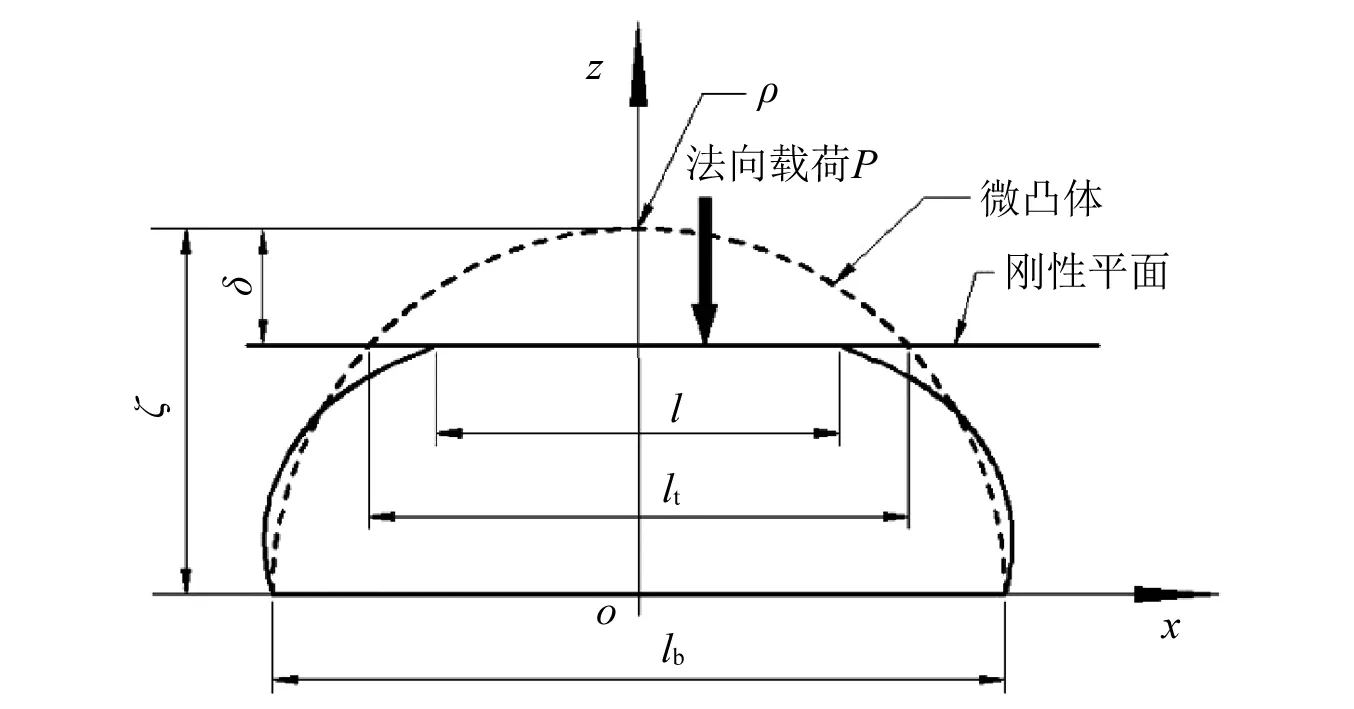
图1 刚性平面引起的微凸体变形简图Fig.1 Schematics of deformation of an asperity by a rigid flat plane

由W-M函数可知，粗糙性是余弦波，变形前的微凸体可以定义为

(1)

式中:D为分形维数;G为特征尺度;lb为基底长度。

由式(1)可得微凸体顶端曲率半径

(2)

微凸体顶端距基底之间的距离为

(3)

微凸体实际变形量为

(4)

根据Hertz理论，作用于微凸体的最大接触压力为

(5)

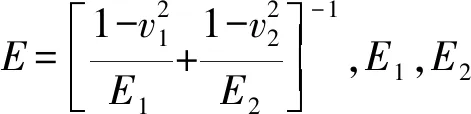
微凸体变形时，微凸体接触面积a为

a=πρδ

(6)

微凸体开始屈服时临界最大接触压力为平均接触压力的3/2倍，若考虑摩擦副之间的相对滑动，则有

(7)

式中:δy为较软材料的屈服强度;Kf为摩擦力修正因子，Kf可由式(8)确定

(8)

由式(2)、式(4)、式(5)和式(7)得微凸体开始屈服时的临界弹性变形量为

(9)

由式(2)、式(6)和式(9)得微凸体开始屈服时的临界弹性变形面积为

(10)

由式(2)、式(4)～式(7)得单个微凸体处在弹性变形下的平均接触压力为

(11)

1.2 摩擦界面单微凸体法向接触刚度

如图1所示，在法向载荷P作用下，刚性表面将沿着z轴的负方向向下移动，由于接触面积很小的微凸体容易满足塑性流动准则，因而处于塑性变形状态，随着载荷的进一步增大，部分小的塑性微凸体发生接触并融合为较大的处于弹性变形状态的微凸体接触[44]。最终，部分微凸体处于塑性接触状态，其在接触过程中耗散接触力所做的功，表现为阻尼作用；部分微凸体处于弹性接触状态，其在接触过程中发生弹性变形而存储接触力所做的功，表现为刚度作用。此时，处于弹性变形的单个微凸体所表现出的刚度为

(12)

由于本文只考虑弹、塑性这两种接触状态，而没有考虑弹塑性接触状态，所以法向接触刚度等于弹性接触刚度，即

kn=ke

(13)

由式(6)、式(11)～式(13)得单微凸体的法向接触刚度为

(14)

1.3 摩擦界面整体法向接触刚度

整个摩擦界面上的法向接触刚度通过对式(14)积分可得，为此引用Wang等[45]分形模型中的面积分布函数。

(15a)

(15b)

式中:al为最大微凸体接触面积；Ar为实际接触面积；ψ区域扩展系数。

区域扩展系数ψ与分形维数D之间的函数关系为

(16)

(17a)

(17b)

(17c)

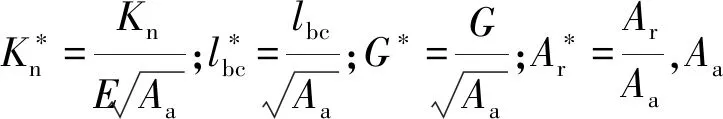
为了与法向载荷联系起来，还需要法向接触载荷与实际接触面积的关系。对此，在本文中引用丁雪兴等研究中的公式。

(18a)

(18b)

(18c)

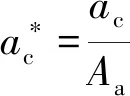
通过对式(17)与式(18)分析不难发现，法向接触刚度与法向接触载荷之间是一种隐函数，中间通过实际接触面积联系起来。

1.4 法向接触刚度模型验证

通过引用Jiang等研究中的试验数据，并与JZZ理论模型进行对比来验证本文模型的正确性。试验材料为铸铁，具体试验计算参数见表1。

表1 试验计算参数Tab.1 Calculation parameters of test

为了便于分析法向接触载荷与法向接触刚度之间的对应关系，把法向接触载荷与法向接触刚度对于无量纲真实接触面积的变化曲线放置在同一张图中，如图2所示。

图2 P,Kn和之间关系图Fig.2 Graph of relationship of P，Kn and

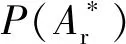
图3 P和Kn之间关系图Fig.3 Graph of relationship of P and Kn

2 理论模型数值分析

将干气密封摩擦界面相关参数代入法向接触刚度模型，分析各参数对其的影响规律，并揭示各参数之间的依存关系。此处采用动环SiC、静环碳石墨进行分析，具体相关参数见表2。由于在本文中将硬质环与软质环的接触简化为刚性理想光滑平面与粗糙表面的接触，以及静环自身结构因素，在表2中个别参数将不予考虑，在分析中取摩擦因数f=0.15。

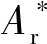
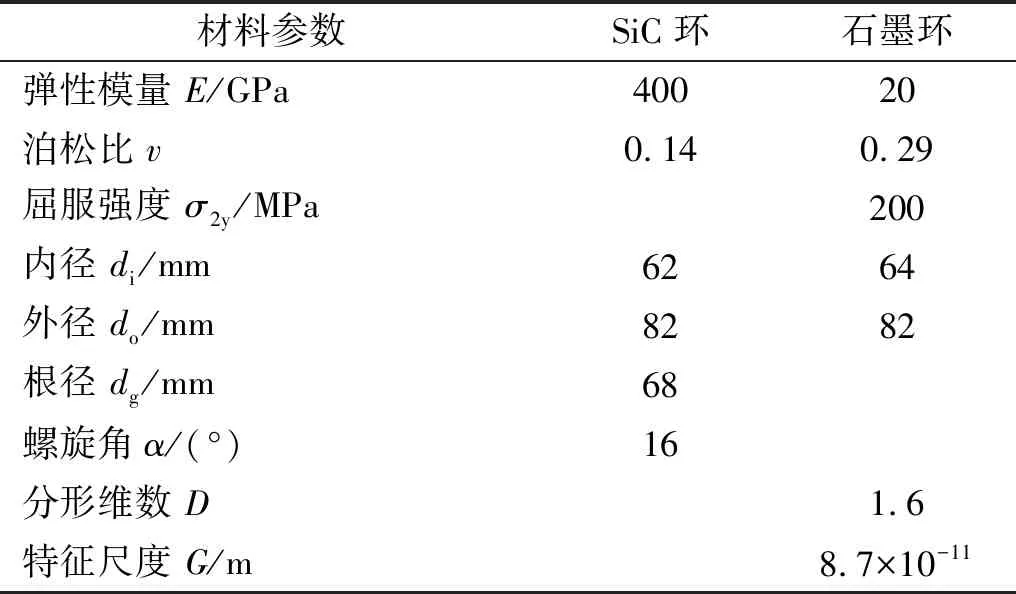
表2 算例计算参数Tab.2 Calculation parameters of example

2.1 分形维数对法向接触刚度的影响

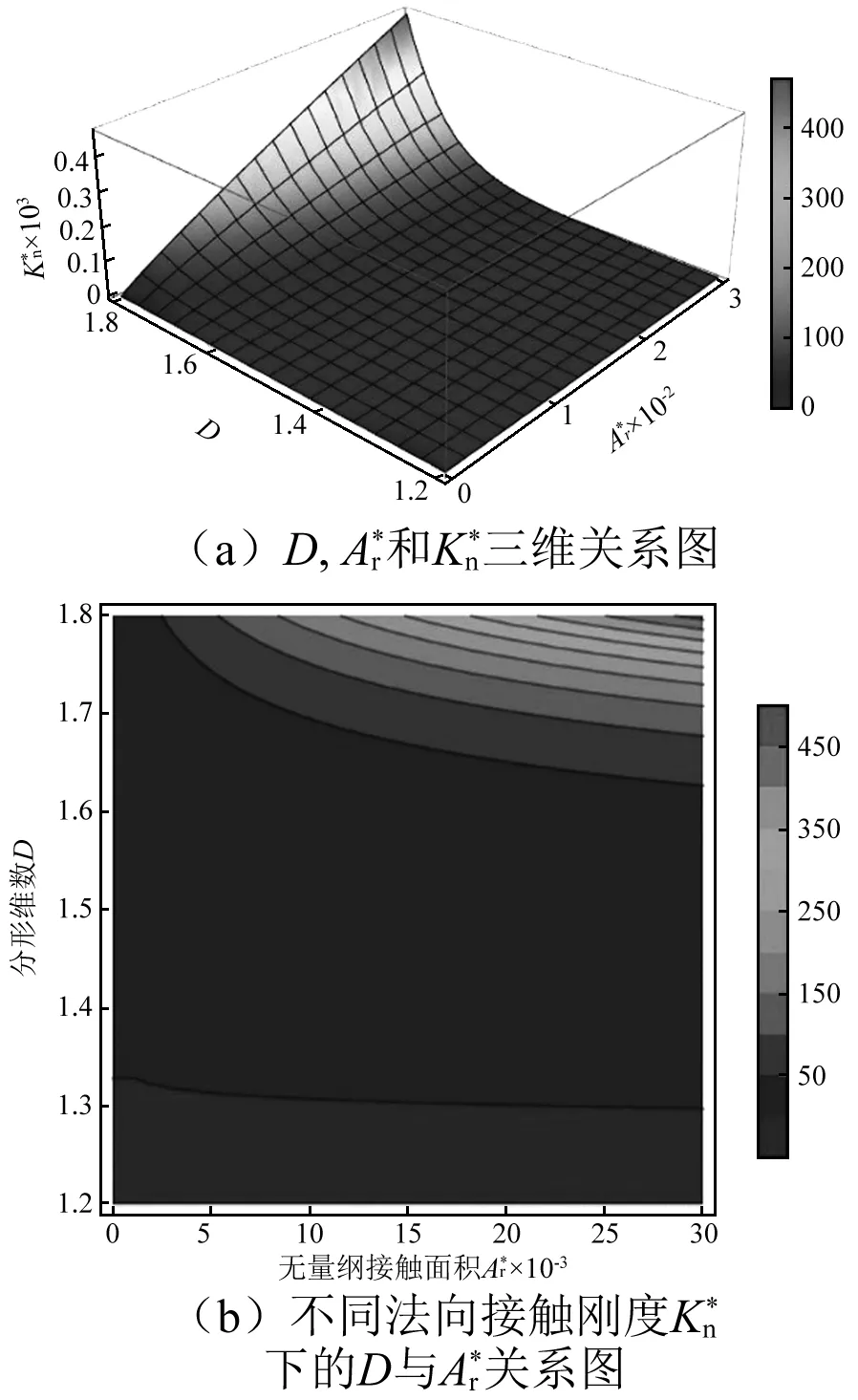
将表2数据代入式(17)，分析分形维数、真实接触面积对干气密封摩擦界面法向接触刚度的影响，他们三者之间的关系如图4(a)所示。同时，为了更加清楚地分析它们三者之间的关系，给出图4(a)中法向接触刚度等高线在其底面的投影，如图4(b)所示。

从图4可以得出：(1)当分形维数D∈[1.2,1.33)，以及D∈[1.33,1.62]时，随着真实接触面积的增大，法向接触刚度在逐渐增大，但在其各自的区间变化较小(在图4中近乎为常数，这主要是在同样的接触条件下，高维数表面产生的法向接触刚度较低维数大，几乎是相差一个数量级，所以在图4中看起来变化较小且近乎为常数)。当分形维数D∈[1.62,1.8)时，随着真实接触面积的增大，法向接触刚度呈非线性逐渐增大，其变化率显著提高，且呈现出分形维数越大，法向接触刚度增大越快。从图4(b)中可以看出D∈[1.4,1.6)时，法向接触刚度的分布相对稳定，其在很小的范围内变化。(2)当接触面积一定时，随着分形维数D的增大，法向接触刚度逐渐增大，特别是在分形维数D>1.6时，这种增大尤为明显与剧烈。因为在无量纲特征尺度G*一定的情形下，分形维数越大，表面越光滑，也即表面越复杂，在同样的接触范围内拥有更多的微凸体，因此，单位接触面积内的承载力将显著提高，最终体现在法向接触刚度的提高。所以在工况一定时，要想获得一定的法向接触刚度，提高分形维数即可。

2.2 特征尺度对法向接触刚度的影响

同样将表2数据代入式(17)，分析特征尺度、真实接触面积对干气密封摩擦界面法向接触刚度的影响，当分形维数D=1.6时，他们三者之间的关系如图5(a)所示。同时，图5(a)中法向接触刚度等高线在其底面的投影，如图5(b)所示。

从图5可以得出：(1)当无量纲特征尺度G*一定时，随着真实接触面积的增大，法向接触刚度逐渐增大。从图5(a)中可以看出，在G*∈[6×10-10,1×10-9)内，这种变化较小，法向接触刚度近似呈线性增大。当G*∈[1×10-10,6×10-10)时，法向接触刚度呈非线性增大，且变化率显著提高。也就是说，具有较低特征尺度的密封环摩擦端面，具有较高的法向接触刚度。这是由于当分形维数一定时，特征尺度越小，摩擦界面越光滑，单位接触面积内的微凸体数量显著增加，相应的其承载能力提高，最终导致整体法向接触刚度的明显提高。(2)当接触面积一定时，随着无量纲特征尺度G*的增大，法向接触刚度逐渐减小。当无量纲特征尺度G*≤6×10-10时，法向接触刚度呈非线性减小，且减小率较高；当无量纲特征尺度G*>6×10-10时，法向接触刚度近似呈线性减小，且变化比较平稳。因为在分形维数一定时，G*越大，也即表面越粗糙，在同样的接触范围内拥有较少的微凸体，其承载能力下降，故整体法向接触刚度就会随着特征尺度的增大而变小。

2.3 摩擦因数对法向接触刚度的影响

当摩擦界面分形维数、特征尺度一定时，分析摩擦因数、真实接触面积对干气密封摩擦界面法向接触刚度的影响，他们三者之间的关系如图6(a)所示。同时，图6(a)中法向接触刚度等高线在其底面的投影，如图6(b)所示。

图和之间关系图Fig.4 Graph of relationship of

图和之间关系图Fig.5 Graph of relationship of

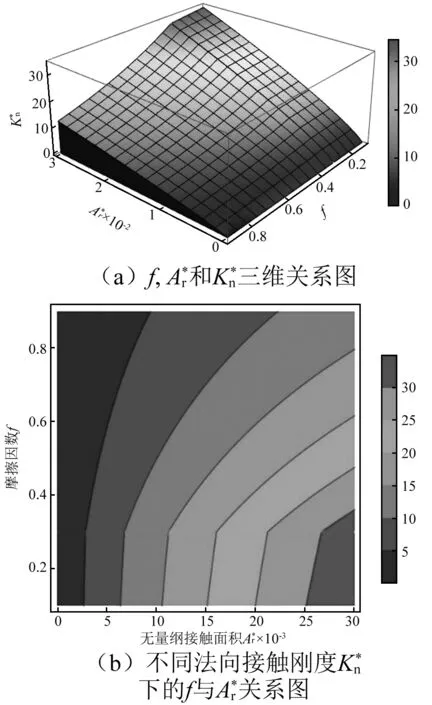
图和之间关系图Fig.6 Graph of relationship of

从图6可以得出：(1)当摩擦因数一定时，随着真实接触面积的增大，法向接触刚度逐渐增大。由式(18)可以看出，真实接触面积与法向接触力是一种正相关关系，所以才会出现真实接触面积越大，法向接触刚度越大的现象。(2)当真实接触面积一定时，法向接触刚度随着摩擦因数f的增大逐渐减小。在f∈[0,0.3]范围内，法向接触刚度以线性的方式减小；而在f∈(0.3,0.9]范围内，法向接触刚度以非线性的方式减小。通过分析式(7)、式(8)不难发现，单个微凸体上的法向接触压力随着摩擦因数f的增大是一种减小的趋势，即摩擦因数的增大对法向接触压力是一种削弱，摩擦因数越大这种削弱程度越大，因此法向接触压力的减小进一步导致法向接触刚度的减小。

3 结 论

(1)从分形理论出发，根据重新建立的微凸体接触变形方式，建立了干气密封摩擦界面法向接触刚度分形模型，完善了干气密封在干摩擦状态下的摩擦振动动力学参量。

(2)法向接触刚度随着分形维数的增大而不断增大。在低维数时，法向接触刚度增加较为缓慢，近似以线性方式增大；而在高维数时，法向接触刚度呈非线性增大，其变化率显著提高。

(3)法向接触刚度随着特征尺度的增大而不断减小。特征尺度较小时，法向接触刚度呈非线性减小；特征尺度较大时，法向接触刚度近似呈线性减小，且变化比较平稳。

(4)法向接触刚度随着摩擦因数的增大逐渐减小。在低摩擦因数范围内，法向接触刚度以线性的方式减小；而在较高摩擦因数范围内，法向接触刚度以非线性的方式减小。相比于分形维数、特征尺度对法向接触刚度的影响，摩擦因数的影响相对较小。

(5)本文在建立模型时，假设密封面分别为一刚性平面和粗糙平面，且忽略了弹塑性变形状态。若想获得更为精确的法向接触刚度模型，今后还需建立两粗糙面之间的微凸体接触变形方式，以及考虑弹塑性变形状态，并进行相关研究。