基于天空区域改进的暗通道先验算法研究

吴宏锷，胡双年

基于天空区域改进的暗通道先验算法研究

吴宏锷，胡双年

（南阳理工学院 数学与统计学院，河南 南阳 473004）

针对天空区域不满足暗通道先验理论从而导致求解的透射率不够准确、去雾后颜色失真的问题，提出一种基于天空区域改进的暗通道先验算法。首先利用像素的分布规律排除白色物体的干扰，解出准确的大气光，再利用暗通道先验理论估计出图像的透射率，然后利用图像的原始信息对透射率进行修正、优化，得到较为准确的透射率图，最后求解得到清晰图像。通过样本实验，说明该算法在细节强度、图像平均梯度和峰值信噪比方面有较好的效果，能作为图像去雾的一种有效辅助手段。

图像去雾；暗通道先验；天空区域

在雾、霾等天气情况下，受到大气粒子的吸收和散射的作用，光在物体表面反射到达相机的成像过程中，会发生散射和吸收等物理变化，光可能偏离原来的路线，从而导致图像的对比度下降，这种降质的图像将严重影响机器视觉系统的识别效果，例如自动监控系统的图像识别等[1]。

图像去雾是一个非常复杂的问题。目前，针对单幅图像的去雾方法主要有两种：一是基于图像增强的去雾方法[2]；二是基于大气物理散射模型的去雾方 法[3]。图像增强是通过增加图像的对比度和亮度来突出图像中的信息，常用的图像增强方法主要有直方图均衡化[4]、Retinex算法[5]、同态滤波算法[6]、小波变换[7]等。图像增强方法只是对图像进行增强处理，且降质过程中伴随着噪声影响，容易造成图像颜色失真；大气物理散射模型的去雾方法是通过研究雾天图像的退化模型来消除雾气对图像的影响，通过获取有效的先验信息，对目标函数添加对应的约束项进行求解，但先验信息的获取是一个不完全约束问题，准确地获取和应用先验信息是此方法的一个难点。

文献[8]通过统计大量室外的有雾和无雾图像，从而提出暗通道先验理论。此理论对大多数有雾图像都能取得较好的结果，但对包含大量天空区域的图像去雾效果较差，且其软抠图优化方法计算过于复杂，因此不少学者在其理论基础上进行了针对性的优化。文献[9]通过中值滤波的方法来替代软抠图算法，虽降低了时间复杂度，但是中值滤波的边缘效果保持不是很理想，在深度不连续的情况下容易出现空洞缺陷。文献[8]对优化方法进行了改进，采用引导滤波的方法来替代软抠图算法，不仅降低了时间复杂度，其边缘效果保持较好。但这些改进方法在处理含有大量天空区域的图片时，去雾效果较差。文献[10]提出一种基于天空识别的暗通道改进算法，该算法通过天空识别的思想来划分天空与非天空的部分，分别对其进行处理，但该算法运行时间较长，并不适合图像的实时处理。文献[11]提出利用引导滤波对天空区域进行分割，通过估计包含天空区域的大气光和透射率，利用中值滤波来消除景物边缘的光晕现象，但分割过程中噪声的干扰容易造成边缘部分图像的失真且运算时间过长。

笔者研究发现：天空区域的元素在颜色空间的分布呈一条直线，利用此规律可求解得到较为准确的大气光。针对文献[8]算法中无法处理天空区域这部分特殊的区域，设计了新的透射率求解公式（下称“改进算法”），同时对求解的透射率图进行了优化。结果表明：改进算法不仅有效处理了天空区域部分的去雾问题，也降低了时间的复杂度。此外，该方法能有效恢复出无雾图像，防止去雾结果中出现的一些伪边缘或颜色失真等问题。

1 雾天图像退化模型

雾天图像可以视为经过大气光衰减的入射光与经过环境散射的散射光的线性叠加，数学模型为

式中，()是退化后的图像，()是清晰图像，()是透射率，是大气光。式中第一项是直接衰减项，反映大气粒子对光的吸收；第二项是间接衰减项，反映环境光的散射。二者线性叠加得到最终退化后的结果。从数学角度而言，就是已知()，求取()。由于等式中包含的未知量多于已知量，因此，必须先利用图像的先验信息求解出大气光和透射率()，其计算步骤为：

（1）结合暗通道先验信息计算大气光；

（2）利用暗通道先验信息估计出大气透射率()；

（3）利用已知的大气光和透射率()，结合退化模型，求取()。

2 基于天空区域改进的暗通道先验算法

2.1 大气光的估计

一般选取天空区域最亮的点作为大气光的值，但是实际情况是：天空区域的亮度可能受到环境因素的影响而显得比较暗，导致选取的值来源于白色物体或颜色较亮的景物，从而错误估计大气光。针对此问题，可以借助退化图像的暗通道来排除白色物体的干扰。

首先选取暗通道亮度值排名前0.1%的区域，然后选取对应原始图像中亮度值最大的像素点作为大气光的值。不过此方法容易受到白色物体或较亮区域的干扰，导致选取的点是非天空区域。通过对200多幅图像梯度特征的分析，发现天空区域的点与非天空区域的点在颜色空间上的分布有显著差别，即天空区域的元素更容易分布在（0，0，0）到（255，255，255）这条对角线上，如图1所示，蓝色点代表的就是天空区域中的像素点，粉色点是非天空区域。

图1 像素空间分布图

为区分天空的像素点，选择设定一个阈值：

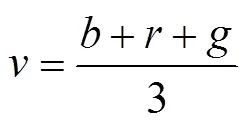
在求取大气光的时候，选取最亮的点是否有效，主要取决于选取的这个最亮的点来自天空还是白色物体。因此，需通过设置的阈值来区分这个点是否来自天空。实验中设置阈值大小为＝36。如果＜36，判定像素点来自天空，否则来自白色物体。

2.2 透射率的求解

在已知大气光的情况下，根据雾天图像的退化模型式（1）可得：

对两边取最小值可得：

式中，表示图像3个通道中的某一个通道。对上式进行最小值滤波运算，由于邻域足够小，可将这个范围内的透射率视为常数。结果如下：

式中，()表示以为中心的邻域。由暗通道先验知识可知：

则()等于：

假定(,)是有雾图像对应的暗通道邻域内最亮的值：

假定(,)是有雾图像对应的暗通道邻域内最暗的值。

式（13）的物理意义在于清晰图像的暗通道值相对于有雾图像较小，可以对有雾图像的暗通道进行适当缩小以使得计算更加准确。式（13）表明：当有雾图像的暗通道图像中(,)的亮度值接近于(,)的值时，清晰图像(,)的透射率的值也是接近于(,)透射率的值；当有雾图像的暗通道图像中(,)的亮度值接近于(,)的值时，清晰图像的透射率的值会接近于(,) 的值。

由式（10）可知，当图像这部分区域满足暗通道先验理论的情况下，本文求解方式就等效于文献[8]的求解方法。如果不满足，透射率()则改写为：

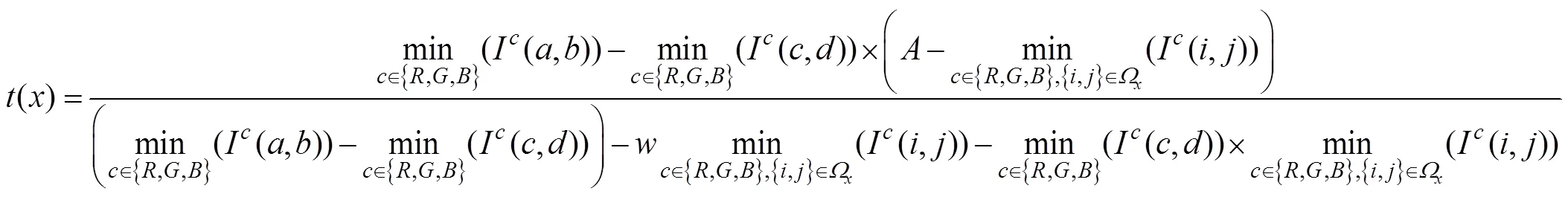
求得透射率过后，可通过引导滤波进行优化。

2.3 清晰图像的求解

求解出相对应的大气光和透射率后，结合雾天图像的退化模型可求解出清晰图像为

为了防止透射率()过小，造成对应的()偏大，可设定一个阈值0，将低于阈的全部阈值等价于阈 值0。

3 实验结果与分析

3.1 透射率图的比较

透射率是指光通过大气后的辐射强度与通过前的辐射强度之比，主要是由全散射系数和景深决定。文献[10]的研究表明透射率的准确度直接关系到图像的去雾效果。文献[11]、文献[12]和改进算法所获取的透射率对比图如图2所示。

利用改进算法得到的透射率图细节更加清晰，边缘变化明显，例如图2中，天安门城楼上的文字和天安门城楼前的景物相较于文献[11]的结果更为清晰，边界清晰度相较于文献[12]的结果有所提高。

3.2 去雾结果的比较

将改进算法输出的结果同文献[11]和文献[12]结果进行对比，如图3所示。

在图3中，相比文献[11]和文献[12]的结果，本文提出的改进算法去雾，图像的对比度明显提高，并且颜色艳丽，并且所拍摄景物的颜色复原后更加真实，而天空部分去雾的结果仍保留雾化状态，更加符合实际。

图2 3种算法透射率的结果对比图

图3 3种算法去雾的结果图

为了更好地评价改进算法的效果，论文采用细节强度[13]、平均梯度[14]和峰值信噪比[15]3种方法，输出结果如表1所示。其中细节强度表示图像的边缘对比度，平均梯度反应图像的细节情况，峰值信噪比表示一幅图像包含的有效信息[16]。

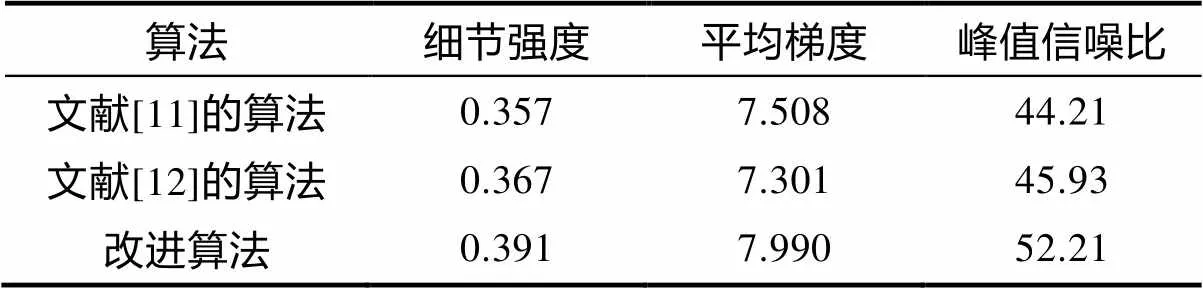
表1 去雾评价指标对比

4 结语

通过对暗通道去雾算法的局限性进行分析后，提出一种改进算法，求解出相对准确的透射率。当有雾图像这部分区域满足暗通道先验理论，这个求解公式就退化成文献[8]的求解方法；当这部分不满足时，求解公式即为改进算法。通过实验验证出了改进算法的去雾效果有一定的提升，尤其是在天空部分。

[1] 宋颖超，罗海波，惠斌，等.尺度自适应暗通道先验去雾方法[J].红外与激光工程，2016, 45(9): 286–297.

[2] POLESEL A, RAMPONI G, MATHEWS V J. Image enhancement via adaptive unsharp masking[J]. IEEE Transactions on Image Processing, 2000, 9(3): 505–510.

[3] LI Xiaoguang. A New Defogging Algorithm Based on Atmospheric Degradation Physical Model[J]. Advanced Materials Research, 2014, 3326(989): 2484–2487.

[4] 吴成茂.直方图均衡化的数学模型研究[J].电子学报，2013, 41(3): 598–602.

[5] 赵晓霞，王汝琳.改进的多尺度Retinex算法及其应用[J].计算机工程，2011, 37(6): 209–211.

[6] 肖俊，宋寿鹏，丁丽娟.空域同态滤波算法研究[J].中国图象图形学报，2008, 13(12): 2302–2306.

[7] 屈稳太，诸静.图像小波变换中的两个关键技术:滤波器的正则性与信号的边界处理[J].浙江大学学报(工学版)，2003, 37(2): 185–189.

[8] HE K, TANG X, SUN J. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence. 2011, 33(12): 2341–2353.

[9] TAREL J P, HAUTIÈRE N. Fast visibility restoration from a single color or gray level image[C]//IEEE,International Conference on Computer Vision. IEEE, 2009: 2201–2208.

[10] 李加元，胡庆武，艾明耀，等.结合天空识别和暗通道原理的图像去雾[J].中国图象图形学报，2015, 20(4): 514–519.

[11] 肖进胜，高威，邹白昱，等.基于天空约束暗通道先验的图像去雾[J].电子学报，2017, 45(2): 346–352.

[12] HE K, SUN J, TANG X. Guided Image Filtering[C]//European Conference on Computer Vision. Springer-Verlag, 2010: 1–14.

[13] FATTAL R. Single image dehazing[C]//ACM. 2008: 1–9.

[14] 汤红忠，张小刚，朱玲，等.结合最小颜色通道图与传播滤波的单幅图像去雾算法研究[J].通信学报，2017, 38(1): 26–34.

[15] 沈逸云，刘春晓，张金栋，等.鲁棒图像去雾的大气光校正与透射率优化算法[J].计算机辅助设计与图形学学报，2017, 29(9): 1604–1612.

[16] WANG J B, HE N, ZHANG L L, et al. Single image dehazing with a physical model and dark channel prior[J]. Neurocomputing, 2015, 149(PB): 718–728.

Research on dark channel prior improved algorithm based on sky area

WU Hong’e, HU Shuangnian

(School of Mathematics and Statistics, Nanyang Institute of Technology, Nanyang 473004, China)

In view of the problem of inaccurate transmittance and color distortion after fog removal due to the lack of dark channel priori theory in sky area, an improved dark channel priori algorithm based on sky region is proposed. Firstly, the interference of white objects is eliminated by the distribution of pixels, and the accurate atmospheric light is obtained, and the transmittance of the image is estimated by the dark channel priori theory. Then, the original information of the image is used to modify and optimize the transmittance, and a more accurate transmittance map is obtained. Finally, a clear picture is obtained by solving the problem. Sample experiments show that the algorithm has better effect in detail intensity, image average gradient and peak signal ratio, and can be used as an effective auxiliary means for image defogging.

image defogging; dark channel priori; sky area

TP 391.4

A

1002-4956(2019)09-0120-04

2019-03-13

国家自然科学基金项目（U1504105）；河南省基础前沿项目（152300410180）

吴宏锷（1972—），女，河南南阳，硕士，副教授，主要研究方向为图像处理。

胡双年（1982—），男，河南南阳，博士，副教授，主要研究方向为数论和图像处理。

10.16791/j.cnki.sjg.2019.09.030