基于HYDRUS-2D模型膜下滴灌棉田不同上口宽排盐浅沟下土壤水盐运移模拟

胡钜鑫，虎胆·吐马尔白，李卓然，穆丽德尔·托伙加

(1.水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052)

新疆，地处中国西北地区，是中国最干旱的地区之一，拥有大面积耕地并广泛应用膜下滴灌技术。然而膜下滴灌技术的使用也产生了一定的负面作用，如土壤板结、土壤中盐分积聚导致的次生盐渍化问题等。为了应对这些问题，新疆地区采取了各种方式，如建设暗管排盐系统，采取春灌、秋灌、冬灌[1-2]等方式对土壤盐分进行淋洗等。

为了改良盐碱土壤及预防土壤由于滴灌引起的次生盐渍化，国内学者展开了各种研究，如李显溦等人研究的暗管排盐技术[3-4]，优化了暗管排盐模式效率不高的问题；周和平[5-7]等人提出“土壤盐分定向迁移”的排盐理论，提出了利用土壤水分蒸发作用使盐分定向向土壤表层迁移，高效排盐；同时还有利用土壤改良剂改良盐碱土壤[8-10]以及利用水动力学原理改良土壤的模式[11]。为了改良新疆北部地区棉花种植区域由于膜下滴灌技术导致的土壤盐碱化问题，本文通过在作物宽行间设置排盐浅沟的方式进行土壤排盐。并通过建立HYDRUS-2D[12-14]模型的方式研究不同上口宽度对排盐浅沟排盐效果的影响。为合理制定土壤排盐模式，减少和改良土壤次生盐渍化提供科学的理论依据。

1 材料与方法

1.1 试验区概况

试验区位于新疆石河子市新疆现代节水灌溉兵团重点实验室，试验区地处干旱地带，夏季高温少雨、冬季严寒，有日照时间长、蒸发量大、降雨量少、温差大等特点，为典型的大陆性气候。年降雨量180～270 mm，年蒸发量为1000～1500 mm。试验区所属的石河子团场常年采取膜下滴灌方式种植棉花。

1.2 试验设计

试验共设置3个测坑和一个大型蒸渗仪。试验中，蒸渗仪与1、2号测坑为2 m×2 m，测坑下边界自由排水，3号测坑为2 m×3 m的自由排水测坑，3个测坑内的土壤含盐率较高，蒸渗仪内土壤含盐率较低。蒸渗仪为1号测坑试验对照组，用于计算和分析土壤的蒸发量及作物蒸腾量。

3个测坑中土壤排盐浅沟的上口宽分别为40 cm、50 cm和60 cm，底宽度均为25 cm，高均为30 cm。蒸渗仪的排盐浅沟布置与1号测坑相同。测坑和蒸渗仪采用相同的灌水定额。实际灌水时间及灌水量见表1。土壤初始含水率及电导率见表2。

表1 实际灌水量

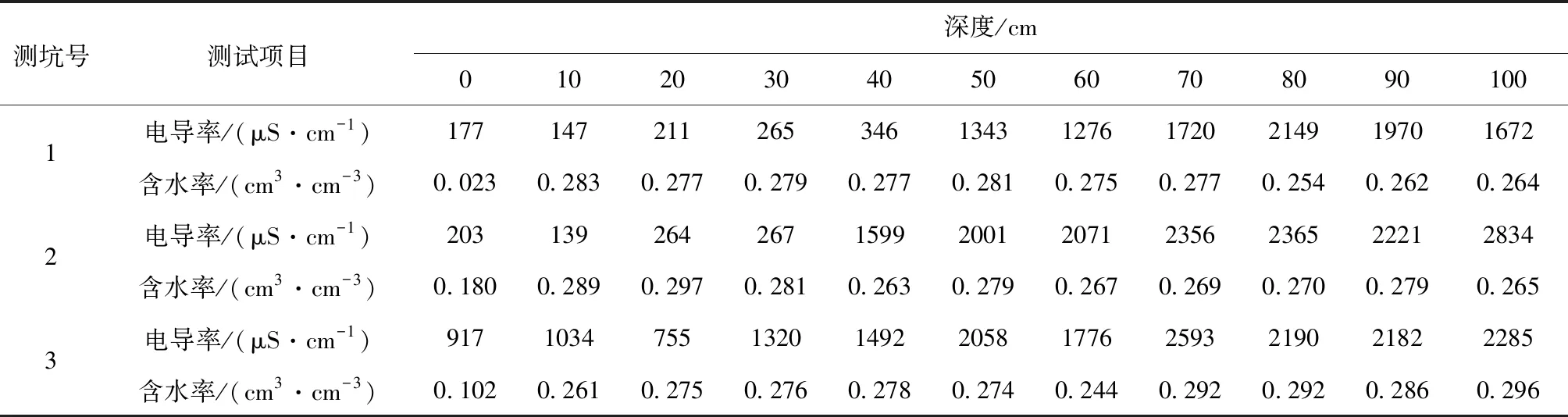
表2 2017年灌溉前土壤剖面含水率和含盐率的分布

2 数学模型建立

在HYDRUS中假设土壤为均质多孔介质，滴灌带每隔30 cm设有一个出水口，每个出水口的湿润半径为30 cm，因此模拟过程中，将滴灌带假设为一条连续出水带，简化模型，x,y方向运动规律进行合并统一，将三维运动简化为二维运动过程。

2.1 模型参数的确定

根据土壤颗粒分析试验所得数据，代入到人工神经网络系统中进行计算，得到模型的水分运动参数如表3。

表3 模型水分运动参数

根据田间试验计算土壤盐分的纵横弥散系数，土壤盐分弥散系数表现了土壤中溶质随着水分运动的变化规律，试验结果见表4。

表4 土壤盐分横纵弥散系数

2.2 水分运动控制方程

试验中假设土壤为均质多孔介质土壤，不考虑热通量变化对水流运动影响。二维水分入渗条件下Richards方程可表述为：

(1)

式中：θ为土壤含水率，cm3/cm3；t为时间 ，d；h为水头压力，cm；x为水平坐标，cm；z为垂直坐标，取向上为正，cm；K(h)为非饱和导水率，cm/h；S(h，x，z)为根系吸水项，cm/cm3·h。

根据Feddes模型来计算，此模型根据根区任意一点的土壤水头压力对植物根区吸水率进行赋值，形式为：

S(h)=α(h)Sp

(2)

式中：Sp为无水分胁迫周期内的吸水率；α(h)是植物根系吸水的无量纲响应函数，定义为：

(3)

h1到h4为影响根系从土壤吸水的不同水头压力,cm。式中：h1为作物厌氧点；h2为最佳水分适宜点；h3为水分胁迫点；h4为作物凋萎点。

2.3 溶质运动控制方程

假设试验用土为均质多孔介质土壤，不考虑热通量变化对水分及盐分运动影响。因此，盐分运动仅随水分运动，对流—弥散方程可表示为：

(4)

式中：θ0为初始含水量，cm3/cm3；xi为第i个点的水平坐标，cm；假定植物根系吸收的溶质可以忽略不计,qi为第i个点水流通量变化,cm/d；c为液体中的溶质浓度，g/cm3；Dij为第i个点的弥散系数，cm2/d；等式右边第一项为由于弥散导致的溶质通量变化；第二项为由于水流的对流导致的溶质通量变化。

2.4 初始条件

2.4.1 土壤水分运动初始条件

θ(x,z,0)=θ0(x,z)

0≤z≤Z,0≤x≤X,t=0

(5)

式中：θ0为初始体积含水率，cm3/cm3。

2.4.2 土壤盐分运动初始条件

C(x,z,0)=C0(x,z)

0≤z≤Z,0≤x≤X,t=0

(6)

式中：C0为土壤初始含盐量，g/kg。

2.5 边界条件

根据实际田间测坑形状在HYDRUS-2D模型中进行模型构建。以1号测坑以及蒸渗仪尺寸为基础，测坑长宽均为2 m，以排盐浅沟中心线为轴，左右呈现对称，为了减少模型运算可以简化模型。将试验区域以排盐浅沟中心线进行划分，对其左侧进行模拟，模拟区域以及有限元划分见图1。根据实际情况对图中各个边界进行边界条件设定。

图1 模型区域及有限元划分(单位：cm)

在HYDRUS中根据图1建立模型，并根据实际田间情况设置各边界的水分运动条件。其中BC边界处中间位置设立2 cm滴灌管入渗区域，其边界条件为变流量边界条件，流量设置与实际灌溉一致。

上边界BC处为变流量边界条件，其平衡方程为：

(7)

下边界AF处为自由排水边界：

θ=θ0

(8)

左右边界AB、EF处为零通量边界条件：

(9)

大气DE边界处为大气边界条件：

(10)

大气边界CD处：

(11)

式中：D(θ)为土壤扩散率，cm2/d；E(t)为蒸腾量，cm/d。

土壤盐分运动与水分运动保持一致性，因此，盐分边界条件与水分边界条件具有相关性。大气边界、滴灌管道布设位置及下边界由于水分通量影响，为通量型边界条件。左右边界AB、EF处由于水分边界条件为无通量边界条件，则盐分遵循相同规律，为无通量边界：

(12)

大气边界CD处：

(13)

大气边界DE处：

(14)

式中，qs为地表水分通量，cm/d；cs为边界流量矿化度，g/cm3。

3 模型的验证

3.1 排盐浅沟水分运动模型验证

通过平方根误差(REMS)、Pearson相关性及显著性对模型的准确度进行检验。Pearson相关性系数的绝对值越大，表明两组数据的相关性越好，根据Pearson相关性系数的分级，相关系数处于(0.8，1]区间范围内时，数据为极强相关；(0.6，0.8]区间范围内时，数据为强相关；(0.4，0.6]区间范围内时，数据为中等强度相关；(0.2，0.4]区间范围内时，数据为弱相关；(0，0.2]区间范围内时，数据为极弱相关或无相关。表5显示了1号测坑处理，40 cm上口宽排盐浅沟各时期取样点含水率实测值与模拟值的对比结果。平方根误差是检验两组数据差别的数据，在相同的数据基础下，平方根误差值越小，两组数据差别越小。利用平方根误差比较实测值与模拟值，具体见公式(15)：

(15)

式中：Mi与Si分别为实测值与模拟值,cm3/cm3；n为观测点数量。

表5 1号测坑各处水分模拟和实测值REMS cm3·cm-3

根据表5显示，不同位置土壤中水分的实测值和模拟值的REMS值与水分值相比均较小，表明土壤模拟的结果较好。对比三个不同取样点的模拟结果，排盐浅沟沟坡处模拟结果差，这是由于取样点位于排盐浅沟坡面之上。在实际取样过程中，为了保障边坡的稳定性，减少对排盐浅沟沟坡的损害，因此取样点往往会有所偏离。其中，滴头处含水率实测值与模拟值的平方根误差范围在0.0059～0.0280，沟坡处平方根误差范围在0.0069～0.0413，沟底处平方根误差范围在0.0010～0.0500，误差值是实测值与计算值之间优化拟合程度定量计算。从时间上，模拟末期平方根误差最大，均达到0.01以上，说明模型准确度有所下降。究其原因，主要是前期影响土壤水分分布的因素较小，且作物根系不发达，实际情况与理想情况相差无几，因而拟合精度较高。而在模拟后期，影响模拟精度的因素众多，无论作物本身还是外界条件，都会对实测值产生影响，造成实测值与模拟值的偏差。

3.2 浅沟排盐盐分运动模型验证

用平方根误差和相关系数对不同日期不同深度土壤的电导率的实测值和模拟值进行相关性验证。表6显示了40 cm宽排盐浅沟各时期滴头处、边坡处、沟底处各时间点取样点电导率实测值与模拟值的对比结果。

根据表6显示，排盐浅沟各处各个时段的电导率的Pearson相关性系数均处于[0.81,1]的区间范围内属于极高度相关。根据表格显示，三组数据在8月31日的模拟结果普遍相关性略差一些，由于8月31日为试验的后期，试验中各种因素会影响到土壤模型的准确性，包括土壤热通量、土壤覆膜的破损以及土壤取样对水分、盐分运动造成的扰动等。6月4日及7月18日均为灌水后测定盐分的日期，模型中，这两天的模拟效果较好，比较明确的体现了土壤中溶质随着水分运动的规律。

表6 40 cm宽排盐浅沟电导率实测值和模拟值验证

注：**在0.01水平(双侧)上显著相关，*在0.05水平(双侧)上显著相关，部分显著性数据因小数位限制无法显示。

4 模型应用与分析

膜下滴灌棉田浅沟排盐模式是利用大气蒸发和土壤中盐随水分运动的原理，将土壤中的盐分通过土壤中的水分运动集中于固定通道，即排盐浅沟。排盐浅沟表层盐分积聚量多，说明其排盐效果最佳。相同情况下，排盐浅沟表层土壤盐分积聚多，在进行冲洗过程中，通过冲水或者刮土带走的盐分越多。排盐浅沟的尺寸可以直接影响土壤的蒸发能力和盐分在排盐浅沟处的积聚能力。

4.1 不同上口宽排盐浅沟生育期水分运动规律

研究土壤模型水分变化规律是研究土壤中溶质运动规律的基础。对不同上口宽排盐浅沟的膜下滴灌棉田生育期土壤水分运移规律进行模拟，对比3种不同处理方式下土壤水分运动规律的区别，为研究其相应的溶质运动规律做基础。

根据模型对3个测坑不同上口宽度排盐浅沟处理下不同深度的水分变化进行模拟，对水分随时间的变化以及各个处理下的不同上口宽进行对比分析绘制各个日期不同处理下土壤含水率剖面图。图2～图5对比了3个处理下在不同日期含水率分布情况。模型的降雨量及土壤灌水量均相同，且土壤中初始含水率设置相同，以保证试验变量。5月10日为播种后20 d，作物生长的苗期，由于雪水化后导致土壤含水率较高因此不需要进行灌水处理。6月3日为第一次灌水日期，即6月2日为第一次灌水前土壤水分数据，6月4日为第一次灌水后时间，处于作物生长的蕾期，8月31日为吐絮期，其数据为最后一次灌水后3 d的数据。

根据图2可以看出，生育期前期3组试验处理中土壤水分变化在水平方向上保持一致，没有明显差别。5月9日发生了1 cm的降雨，导致排盐浅沟中水分增大，在此情况下60 cm上口宽处理下，排盐浅沟受到降雨影响较其他两个处理大。土壤中含水率整体呈现由上至下增大的情况。此现象是由于春季冰雪融化导致播种前土壤中整体含水率较高。播种后，土壤中的水不断下移至下方自由排水边界。排盐浅沟土壤表层则存在较少量的蒸发现象，导致上层土壤含水率低于下层土壤。

图3显示的是6月2日第一次灌水前土壤整体含水率的情况。5月份至6月初，气温较低且日照辐射较少，土壤蒸发量较低，作物生长处于蕾期，作物的蒸腾作用较低。随着作物的生长，土壤中的水分随着蒸发和下移不断减少。这一时期，土壤中水分向自由排水边界移动的速度较小，土壤整体含水率较大。相比上一观测阶段，土壤中排盐浅沟处土壤含水率明显下降。

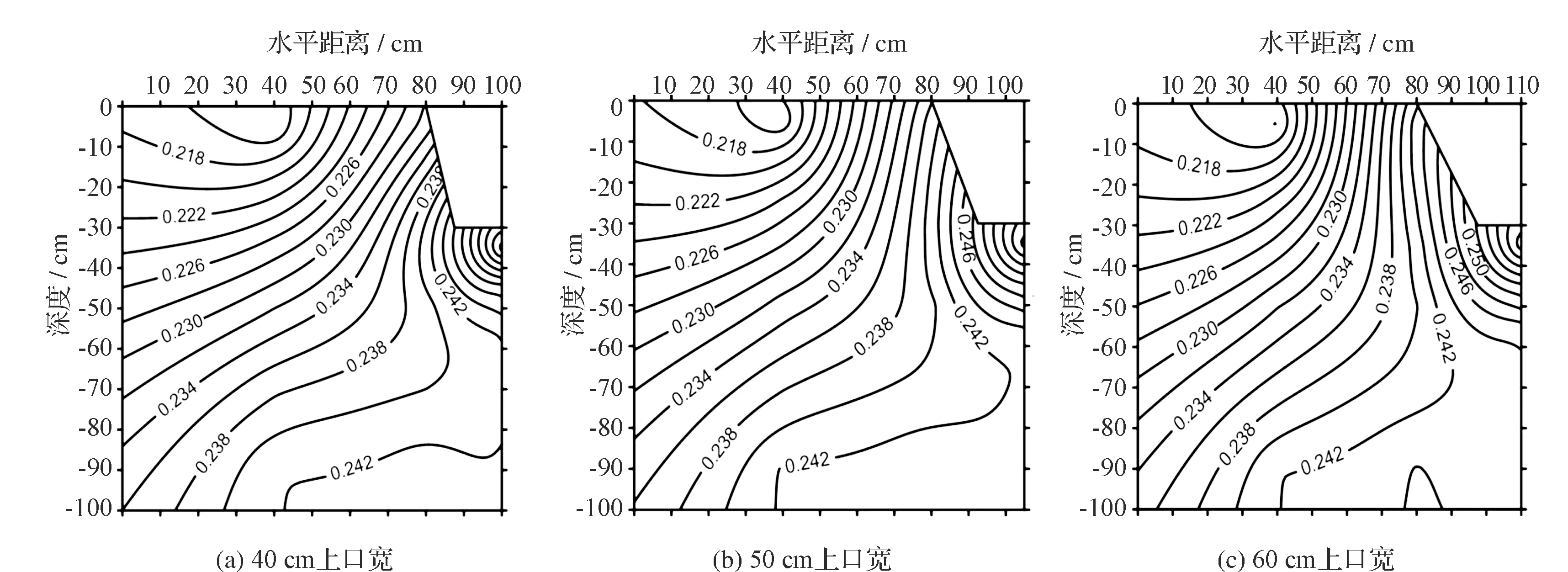
图2 5月10日不同上口宽浅沟土壤含水率剖面图(单位：cm3/cm3)

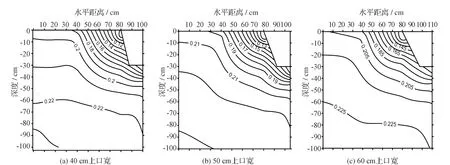
图3 6月2日不同上口宽浅沟土壤含水率剖面图(单位：cm3/cm3)

图4 6月4日不同上口宽浅沟土壤含水率剖面图(单位：cm3/cm3)

图5 8月31日不同上口宽浅沟土壤含水率剖面图(单位：cm3/cm3)

图4显示的是6月4日第一次灌水后土壤含水率的变化情况，根据模拟结果可以看出，灌水后，土壤中含水率的等含水率线由横向趋向于竖直状态。在6月4日，为土壤中灌水后一天因此土壤中水分主要停留在土壤表层下20～40 cm处，土壤中的水分扩散还未影响到排盐浅沟边坡。灌水后，相比于50 cm上口宽及60 cm上口宽，40 cm上口宽土壤最高含水率位置深度更浅，说明其水分的纵向运动弱，更利于水分的横向运动。

图5为8月31日不同上口宽浅沟含水率的剖面图，作物生长处于吐絮期，最后一次灌水日期为8月29日。从图中可以看出，灌水后两天，灌溉水竖直向下运运动并逐渐向水平方向扩散，且主要向左边界扩散。灌水后3 d，相比于50 cm上口宽及60 cm上口宽，40 cm上口宽土壤水分整体分布更均匀，土壤水分的横向运动较其他两个处理更明显，土壤排盐浅沟处含水率更高。

4.2 不同上口宽排盐浅沟生育期盐分分运动规律

土壤中盐分随着水分的运动而运动，生育期内，土壤中盐分随着灌水不断向下淋洗。由于蒸发作用和作物吸水的影响，土壤中的盐分随着水分的变化在不断变化。图6～图9是不同时期土壤内盐分空间分布情况。

图6～图8所示为膜下滴灌棉田未灌水时期，土壤盐分在竖直方向上由上至下呈现递进式分布，这是由于初始设置时，为与实际情况相符合，借用田间试验初次测量的土壤盐分电导率，设置土壤整体电导率为上小下大。由于土壤初始含水率较高，而地下埋深较深，土壤中的水分会由于重力向模型下边界移动，同时，土壤内溶质随着土壤水分的下移，在土壤中40～60 cm处积累。

图6～ 图9是生育期内不同时段的土壤剖面电导率分布情况。3个处理下滴头位置土壤盐分的淋洗作用均较为明显，滴头下方盐分电导率出现折线形变化。盐分运动随着每次灌水及蒸发运动，盐分运动基本呈现随着每次灌水逐渐下移的情况。随着生育期向后进行，土壤中的盐分主要向50～80 cm移动，使得此处电导率等值线密集。在生育期期间内，浅沟处盐分随着水分的蒸发不断向浅沟附近积聚，在浅沟边坡处及沟底位置形成明显的盐分累积层。对比3个处理可以得出，在浅沟上口宽为40 cm时，相比较于其他两个处理，盐分在排盐浅沟坡处的积聚较好。

对比水分分布图和盐分分布图可以得到，盐分分布受到水分变化影响十分明显。在滴头位置，土壤无蒸发，且有间断性的灌水，使得滴头下方垂直处土壤盐分在生育期呈现持续下降趋势。由于土壤水分在排盐浅沟边坡及排盐浅沟沟底蒸发，水分不断向排盐浅沟位置移动，同时土壤盐分也在不断随着水分的横向运动向排盐浅沟运动，并在排盐浅沟坡附近聚集。土壤盐分运动和水分运动有较好的拟合性。

5 结 论

本文以测坑种植滴灌棉花试验为基础设置排盐浅沟，并通过数值模拟研究其排盐效率问题。根据试验在HYDRUS-2D软件中建立的模型，模拟排盐浅沟的膜下滴灌棉田在设置不同排盐沟上口宽时生育期土壤水盐运移规律，利用Excel、Spss18.0、Surfer11等软件对膜下滴灌棉田设置排盐沟后土壤水盐分布规律进行分析，对比土壤盐分积累及其在排盐浅沟处的分布情况，主要结论如下：

(1)利用HYDRUS-2D软件构建土壤水盐运移模型，利用实测数据与模拟数据进行对比分析以确定模型精度。通过均方根误差、Pearson相关性分析等方法可以得出，生育期期间模型和实测值有较好的拟合性，模型具有一定的可靠性。各时间段，土壤盐分模拟的相关性系数均在[0.81,1]区间范围内，属于显著性相关。

(2)根据模型对不同上口宽排盐沟积聚盐分的能力进行对比，可以得出，当上口宽较小时(上口宽40 cm)，土壤盐分主要积累在排盐沟坡中下部位，并在排盐沟沟底达到最大值。当上口宽较大时(上口宽60 cm)，土壤盐分主要积累在排盐沟底部，并且其底部盐分积累量大于其他两种处理方式。总体而言，相较于50 cm上口宽和60 cm上口宽，40 cm上口宽的排盐浅沟与大气接触面积积累盐分更多，盐分累积效率更高，排盐效果更好。

图6 5月10日不同上口宽浅沟土壤电导率剖面图(单位：μS/cm)

图7 6月2日不同上口宽浅沟土壤电导率剖面图(单位：μS/cm)

图8 6月4日不同上口宽浅沟土壤电导率剖面图(单位：μS/cm)

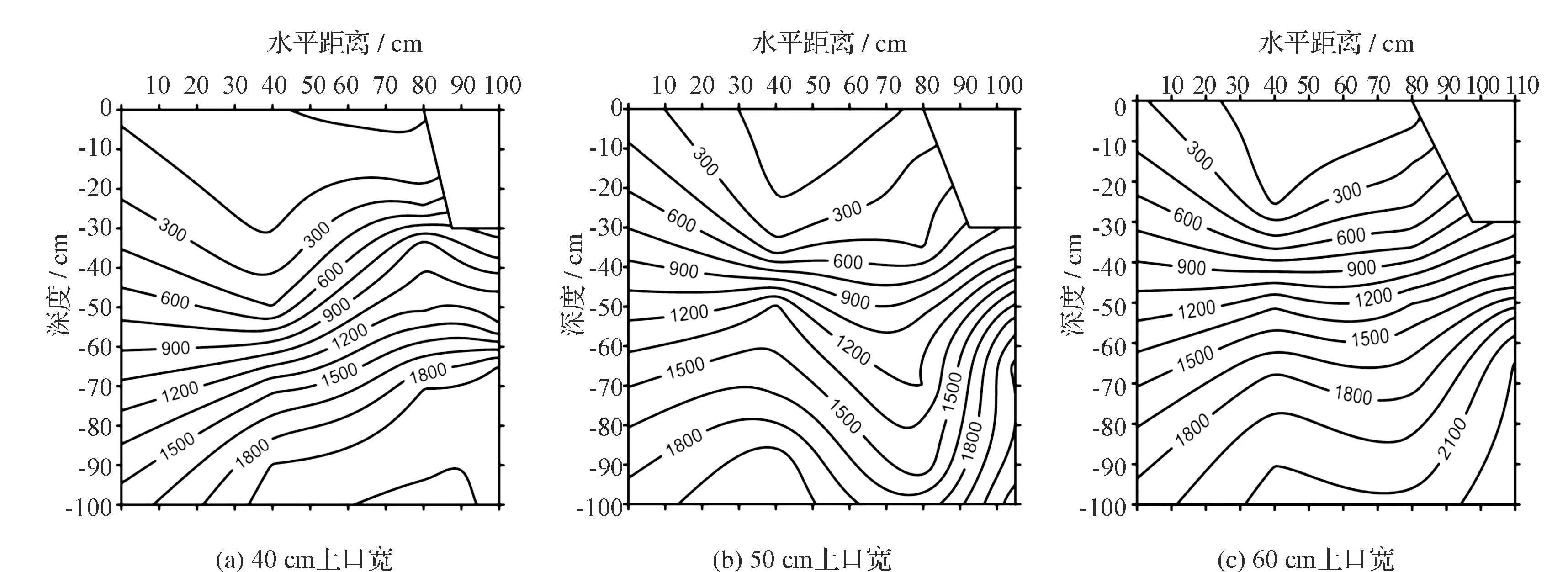
图9 8月31日不同上口宽浅沟土壤电导率剖面图(单位：μS/cm)