基于客观标准的有向哈斯图技术在地下水水质评价中应用

彭 琪，张 强，张 宇，唐金平，何文君，刘映春

(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059；2.广东省财经职业技术学校，广东 佛山 528231)

据统计，我国地下水资源量仅占全国水资源总量的31%，却维持全国近70%的人口饮用和40%的农田灌溉，可见其在保证居民生活用水、社会经济发展和生态环境平衡等方面起的作用不可小觑[1]。然而随着我国工业化与都市化进程，地下水的污染问题日趋显著。因此，选取客观、有效的地下水水质评价方法是非常必要的，合理的评价结果对地下水资源的开发利用具有重要意义。

传统的综合水质评价方法，通常首先对各评价指标进行赋权，再根据不同方法理论进行等级归类。但值得注意的是，不同的赋权方法得到的权重往往不一致，各评价指标权重的取值大小直接关系到最终的评价结果，对于如何才算合理赋权等争议问题也一直存在。为此引入D-HDT对地下水水质进行评价研究，合理规避了这一问题，为地下水水质评级工作开辟新思路。

1 有向哈斯图技术

D-HDT源于离散数学的序理论，表示为有限偏序集的数学图表[2]。在D-HDT中，对于m个样品，n个测度构成矩阵A=[aij]m×n，先按其测度对矩阵列进行排序，通过归一化后得到偏序标准矩阵C=[cij]m×n，然后经构造的函数关系式获得邻接布尔矩阵F=[fij]m×m，再将矩阵F转化成关系矩阵HR，由关系矩阵HR经过一系列的拓扑运算得到层次分明的有向哈斯图[3]。

在环境工程领域中，D-HDT常用于多指标系统的排序，确定环境污染物的敏感性、优先等级及其空间分布水平等[4-6]。本次将其引入地下水水质评价中，以拓扑层级图的形式展示水质的好坏，其效果相对于传统用表格、数学公式及文字等诠释方式显得更直观。

具体评价步骤如下：

(1)确定评价指标集及分级标准。地下水环境质量评价涉及指标众多，不同的地下水系统中水质指标对地下水环境的影响不同，评价指标的合理选取既可以避免忽略一些关键污染指标，也可以简化部分评价的工作量。地下水水质分级标准参考《地下水质量标准(GB/T 14848-2017)》。

(2)指标数据处理。由于D-HDT最终结果只能反映样品之间的优劣层级排序，而无法获得某个层级具体归为哪一级别，为弥补这一遗憾，按照《地下水质量标准(GB/T 14848-2017)》构造5组(S1-S5)标准等级(Ⅰ-Ⅴ)样品数据，并将其加入到待评样品数据中，构成一个初始数据矩阵A=[aij]m×n，然后利用极差处理法将初始数据矩阵A归一化获得标准矩阵B=[bij]m×n。

(3)指标权重排序。本方法主要依靠权重的顺序来进行偏序处理，故其顺序可直接影响评价结果的准确性。虽然不同的方法获得的权重大小不同，但是在权重排序上往往会一致[7]。选择合适的计算方法获得各个指标的权重，然后由大到小依次排序，标准矩阵B相应的列也随之改变，得到偏序标准化矩阵C=[cij]m×n。

(4)建立邻接布尔矩阵。在建立邻接矩阵之前，首先要对偏序标准化矩阵C=[cij]m×n转换成蕴含权重信息的方案决策矩阵D=[dij]m×n。文献[8]提出对于含有m个方案n个指标的决策问题，在各评价指标的权重顺序满足ω11>ω12>…>ω1n的条件下，可通过式(1)计算获得累加决策矩阵D=[dij]m×n。

D=[dij]m×n=CE

(1)

(2)

式中：E为上三角全为1的矩阵。

建立邻接布尔矩阵通常是将累加决策矩阵D各样品相互比较判断得到[9]，其中样品i与样品j要比较两次，对于整个评价系统来说存在m个样品则要比较m(m-1)次，而样品自身则不需要比较，即邻接布尔矩阵的对角线上的值通常用0来表示，其他位置的值由式(3)比较关系求得，即当j行中每一个值均大于i行中每一个值时，fij=1，否则fij=0。由此获得邻接布尔矩阵F=[fij]m×m，由于邻接布尔矩阵F表示的是样品间的比较关系，故矩阵的行与列均代表样品。

(3)

(5)计算Hasse矩阵。该部分可通过matlab软件实现。首先通过邻接布尔矩阵F与单位矩阵I相加得到相乘矩阵G，然后对相乘矩阵G进行布尔连乘运算，直到运算结果矩阵不发生变化，便得到可达矩阵R；最后再通过文献[10]给出的可达矩阵R与Hasse矩阵的转化关系式(4)进行布尔运算得到Hasse矩阵。

HR=(R-I)-(R-I)2

(4)

式中：R为可达矩阵；HR为Hasse矩阵；I为单位矩阵；(R-I)2为布尔运算。

(6)绘制有向Hasse图，分析评价结果。Hasse图能够可视化地表达出Hasse矩阵中的覆盖关系，利用带有标志的圆将存在覆盖关系的样品组用线连接起来。由于Hasse图是有方向的，所以仅在一个方向读取，文献[11]详细介绍了其可视化所遵循的原则。结合预先设定的五组标准等级样品，分析有向Hasse图，获得评价结果。

2 实例应用

2.1 数据处理

按本次选取的评价指标，构造的5组(S1-S5)标准等级(Ⅰ-Ⅴ)样品数据表1，然后将其加入到13组待评价样品中，构成一个18组样品的初始数据矩阵A=[aij]18×8，再利用极值处理法将初始数据归一化获得标准化数据矩阵B=[bij]18×8。

表1 标准等级样品

Tab.1 The sample of standard grade

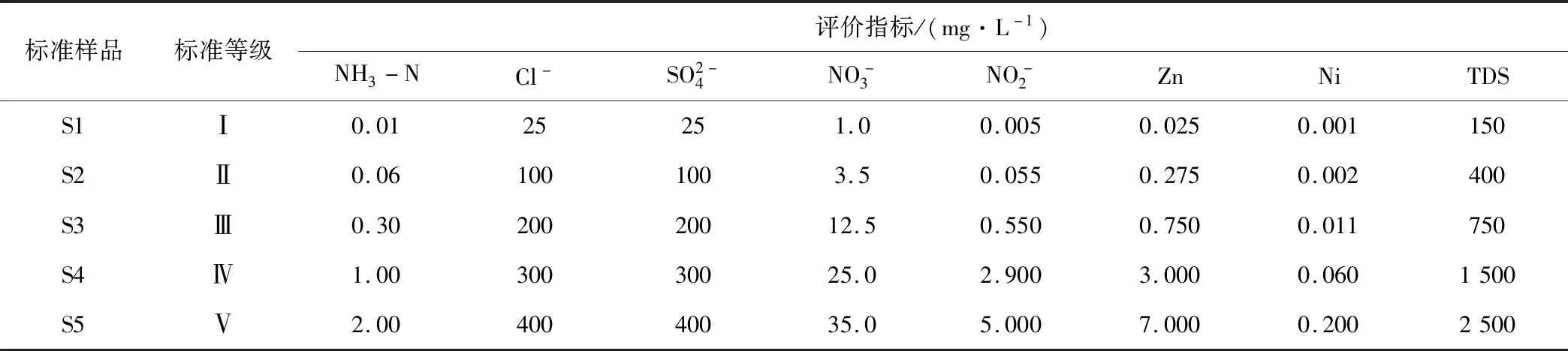
标准样品标准等级评价指标/(mg·L-1)NH3-NCl-SO2-4NO-3NO-2ZnNiTDSS1Ⅰ0.0125251.00.0050.0250.001150S2Ⅱ0.061001003.50.0550.2750.002400S3Ⅲ0.3020020012.50.5500.7500.011750S4Ⅳ1.0030030025.02.9003.0000.0601500S5Ⅴ2.0040040035.05.0007.0000.2002500

2.2 指标权重排序

采用熵权法赋予各评价指标权重，其重要性排序见表2。再根据权重排序调整标准化数据矩阵B=[bij]18×8，使其指标顺序与权重排序一致，获得表3偏序标准化数据矩阵C=[cij]18×8。

表2 指标权重排序

Tab.2 Order of indicator weights

评价指标NH3-NCl-SO2-4NO-3NO-2ZnNiTDS指标权重0.1500.0430.0160.2360.3130.1740.0410.027权重排序45821367

表3 偏序标准化数据

Tab.3 Partial order standardized data

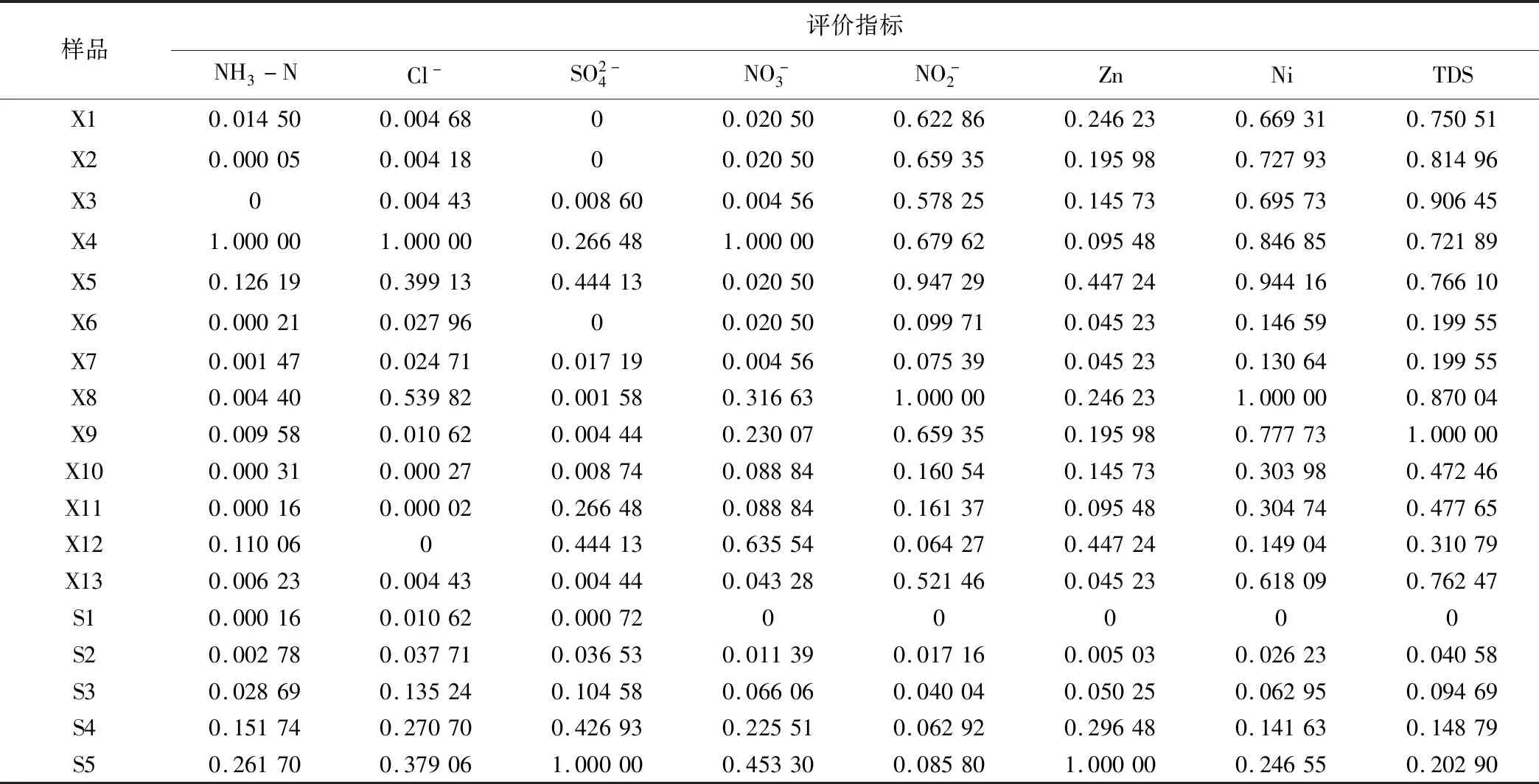
样品评价指标NH3-NCl-SO2-4NO-3NO-2ZnNiTDSX10.014500.0046800.020500.622860.246230.669310.75051X20.000050.0041800.020500.659350.195980.727930.81496X300.004430.008600.004560.578250.145730.695730.90645X41.000001.000000.266481.000000.679620.095480.846850.72189X50.126190.399130.444130.020500.947290.447240.944160.76610X60.000210.0279600.020500.099710.045230.146590.19955X70.001470.024710.017190.004560.075390.045230.130640.19955X80.004400.539820.001580.316631.000000.246231.000000.87004X90.009580.010620.004440.230070.659350.195980.777731.00000X100.000310.000270.008740.088840.160540.145730.303980.47246X110.000160.000020.266480.088840.161370.095480.304740.47765X120.1100600.444130.635540.064270.447240.149040.31079X130.006230.004430.004440.043280.521460.045230.618090.76247S10.000160.010620.0007200000S20.002780.037710.036530.011390.017160.005030.026230.04058S30.028690.135240.104580.066060.040040.050250.062950.09469S40.151740.270700.426930.225510.062920.296480.141630.14879S50.261700.379061.000000.453300.085801.000000.246550.20290

2.3 邻接布尔矩阵F及Hasse矩阵

利用上述偏序标准化矩阵C经式(1)得到累加决策矩阵D，再由式(3)建立表4邻接布尔矩阵F，通过连乘法得到可达矩阵R，再经式(4)进行布尔运算获得表5 Hasse矩阵HR。

表4 邻接布尔矩阵F

Tab.4 Adjacency boolean matrixF

M18×18X1X2X3X4X5X6X7X8X9X10X11X12X13S1S2S3S4S5X1000110000000000001X2000110011000000001X3000110011000000001X4000000000000000000X5000100000000000000X6000110010001000111X7000110010001000111X8000100000000000000X9000110000000000001X10100110011001100011X11000110010001000011X12000110000000000001X13000110001001000001S1100111111001001111S2000110010001000111S3000110000000000011S4000100000000000001S5000100000000000000

表5 Hasse矩阵HR

Tab.5 Hasse matrixHR

M18×18X1X2X3X4X5X6X7X8X9X10X11X12X13S1S2S3S4S5X1000010000000000001X2000000011000000000X3000000011000000000X4000000000000000000X5000100000000000000X6000000010001000100X7000000010001000100X8000100000000000000X9000010000000000001X10100000010000100010X11000000010001000010X12000010000000000001X13000000001001000000S1100001101000001000S2000000010001000100S3000010000000000010S4000000000000000001S5000100000000000000

2.4 有向Hasse图

将表5 Hasse矩阵经拓扑运算转化为层级关系可视化的有向Hasse图，见图1。

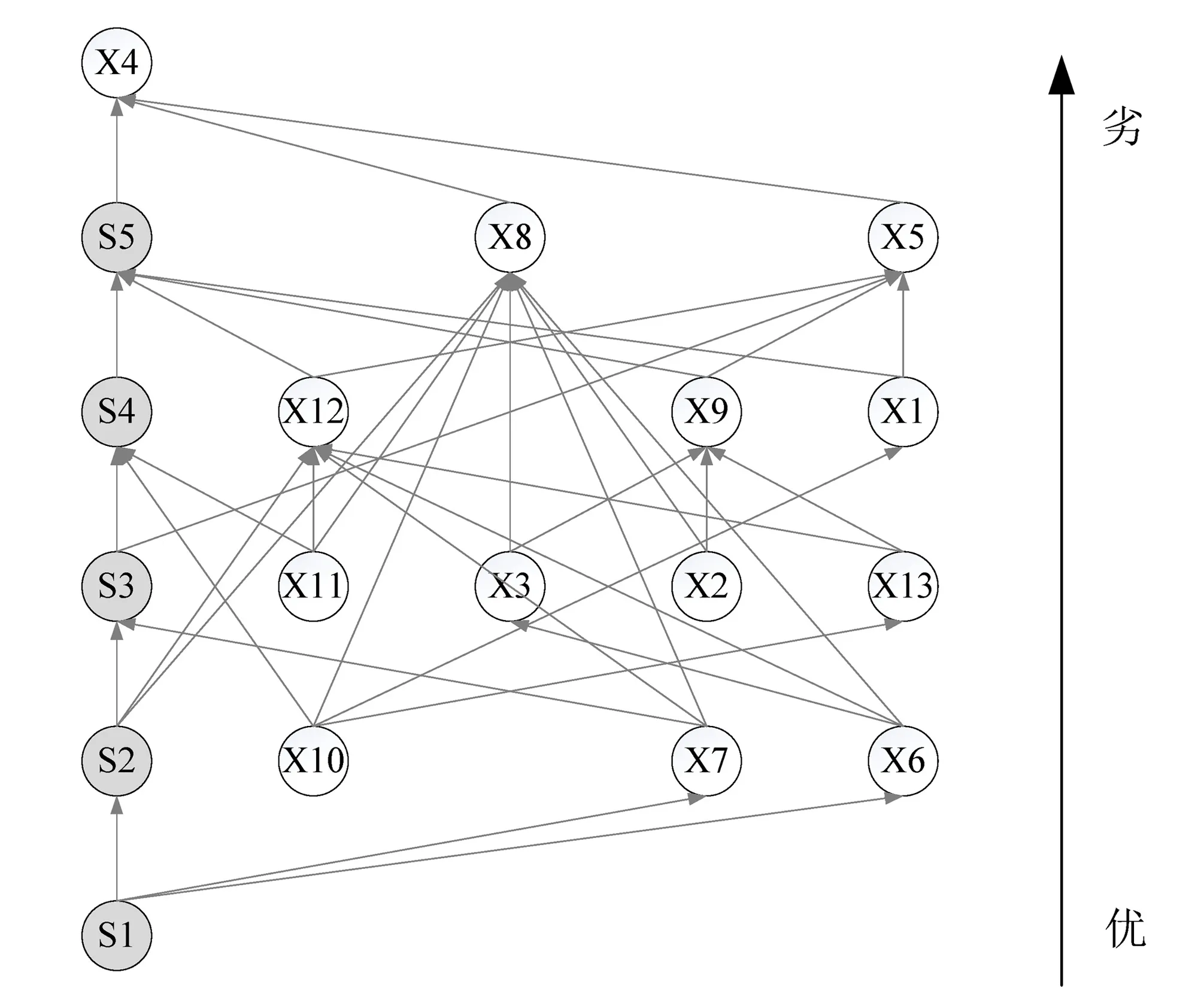
图1 有向Hasse图Fig.1 Directed-Hasse diagram

2.5 结果分析

图1已将样品间的分层及聚类关系直观的显现出来，18个样品分为6个层级，从下往上水质由优到劣。第一层集：S1；第二层集：S2、X10、X7、X6；第三层集：S3、X11、X3、X2、X13；第四层集：S4、X12、X9、X1；第五层集：S5、X8、X5；第六层集：X4。

其中S1～S5为预先设计的标准样品，对应级别为Ⅰ～Ⅴ。图1清晰显示，S1～S5经有向哈斯图方法分层级与聚类后，其层级顺序与对应水质级别一致，即第一层集----Ⅰ级、第二层集----Ⅱ级、第三层集----Ⅲ级、第四层集----Ⅳ级、第五层集----Ⅴ级，相应的各个样品的评价等级也显而易见。其中X4样本位于第六层集，已经超出了S5的级别，属于水质极差的那种，鉴于《地下水质量标准(GB/T 14848-2017)》将水质定为了五个级别，故将其质量划归为Ⅴ级。

为验证评价方法的可行性，现将此次评价结果与文献[12]评价结果作对比，见图2。经比较，基于客观标准的有向Hasse图技术得到的评价结果，既没有像超标权-贝叶斯法那样仅考虑单个污染指标与标准值之间的关系而忽略整个样品体系之间的联系，也没有像熵权-贝叶斯法那样只考虑到整个样品体系之间的联系而降低异常指标值的影响，其整体评价结果介于这两种方法之间，反映出评价区域水质属于中等偏上情况，评价结果更符合客观现实。

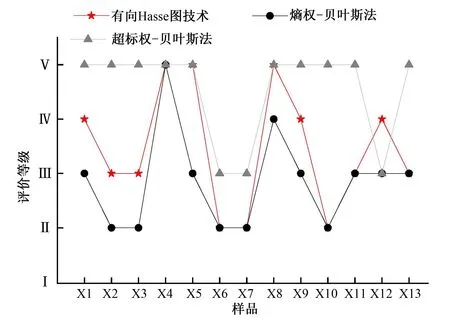
图2 评价结果对比图Fig.2 Comparison of evaluation results

3 结 语

(1)针对地下水水质评价特点，依据客观标准构造的五组标准等级样品弥补了D-HDT在地下水水质评价中无法获得某个层级具体归为哪一级别的遗憾。5组标准样品在有向Hasse图中的分布层级顺序，S1～S5依次由下往上排列，也进一步验证了此次评价方法的可靠性。

(2)基于客观标准的D-HDT解决了以往水质评价中赋权争议的问题，仅需评价指标权重顺序即可进行评价。客观标准与有向Hasse图的结合使得评价结果可视化、更客观，充分展现了本次研究的准确性及优越性，为今后地下水水质评价提供了新思路。