等间距底锚巷道层状底板变形失稳力学机理

郑文翔，卜庆为，王 超，鲍先凯

（内蒙古科技大学 矿业与煤炭学院，内蒙古 包头014010）

底鼓是煤矿巷道支护的老问题，是煤矿井巷中经常发生的1 种动力现象，在底鼓机理与治理方面一直得到众多专家学者的关注[1-4]。巷道层状底板及其底鼓机理是底板岩层在平行层理方向的压力作用下，向底板临空方向挠曲而失稳；底板岩层的分层越薄，巷道宽度越大，所需的挤压力越小，越容易发生挠曲性底鼓[5-6]。对于层状底板鼓起的控制方法也较多[7-9]，如：锚杆、锚杆+锚索、锚注、锚杆+混泥土等。由于力学性质差异的岩层组成了层状结构，使得各岩层显现出不同程度的变形破坏，任意分层的破坏均会造成支护体系失效，因此，研究层状底板变形失稳力学机理具有重要的理论价值。

李传明等[10]针对薄分层软弱底板巷道围岩变形失稳难题，综合理论分析、力学计算、数值模拟、井下试验及现场实测方法，详细研究了薄分层软弱底板巷道压曲失稳机理及控制技术；鲁海峰等[11]将底板层状岩体视为横观各向同性连续体，根据煤层上覆载荷分布特点，推导出了煤层采动后的底板任一点应力解析解，并分析了横观各向同性底板变形参数的各向异性度对应力分布规律的影响；张志雄等[12]采用有限元法对层状岩体中直墙拱形巷道进行了数值模拟。着重讨论了层状岩石弹性模量和岩层倾角等各向异性因素对围岩应力场的影响。贾蓬等[13]研究了层状顶板巷道围岩变形破坏；翟晓荣等[14]采用FLAC3D模拟研究了不同软硬组合特性底板采后渗透性的变化特征，得到软硬相间岩层组合底板的阻水效果最好，软硬型底板最差。只注重底板的加固而忽略层状底板的破断力学机理，致使层状底板出现离层、破断，整体强度大大降低，层状底板将在两帮形成的二次水平应力作用下失稳并产生底鼓。为此，结合实际矿井建立等间距底锚巷道层状底板力学模型，应用力学理论分析其力学机理，构建层状底板任分层鼓起失稳的力学判定准则，并进行反验与分析评价，此研究为层状底板变形失稳提供了便捷、准确的预判方法，为支护方式、支护参数的选取提供理论依据。

1 工程概况

常村矿主采煤层为3#煤层，位于山西组的中下部，煤层平均厚度为3.01 m，煤层倾角平均6°，属于近水平煤层。煤层直接顶板为灰黑色粉砂岩，节理裂隙发育且易破碎，其上为灰白色厚层中粒砂岩、砂质泥岩、细砂岩，底板多为深灰色粉砂岩、中（细）粒砂岩，且呈层状分布，采取底锚措施后底鼓量仍较为严重。S6 采区2#回风上山沿顶板掘进，巷道设计断面为矩形，净宽5.0 m，净高3.5 m，净断面17.5 m2，其支护布置如图1。

图1 锚杆和锚索联合支护断面图

2 等间距底锚巷道层状底板稳定性力学机理

2.1 层状底板压曲作用机理

对于层状赋存的底板，其底鼓程度取决于各分层的稳定性及位移量，各分层底部均承受垂直向上的分布力，两端承受水平力的作用，且端角处出现高的应力集中[15]。由于各分层岩性的不同，致使受力出现差异，任一分层失稳失去承载能力后，必然引起底板岩层内的应力重分布，直至达到1 个新的平衡，在两帮岩体的挤压作用下向巷内弯曲变形、断裂，整体承载能力降低，锚杆不能有效地发挥其锚固效力，乃至支护体系失效，底板仍会鼓起。

2.2 等间距底锚巷道层状底板力学模型

层状底板力学模型如图2，结合实际情况进行基本假设：将等间距底锚层状底板形成的一体锚固体视为组合岩梁结构，将组合岩梁结构简化为左右两端可动，但不发生转动的情形；视组合岩梁结构的介质为弹性状态，且忽略介质自身岩重的影响。

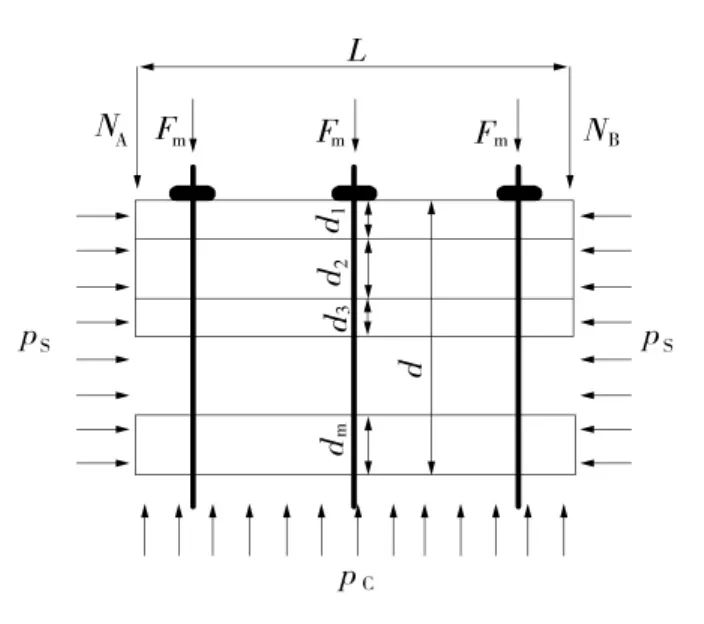
图2 等间距底锚巷道层状底板力学模型

图2 中L 为底板跨度，m；Fm为底板锚杆锚固力，MPa；NA、NB为端部支撑力，kN；pS为组合岩梁结构侧向水平应力，MPa；pC为底部所承受的均匀载荷，MPa；d1、d2、d3、…、dm分别为第1 分层厚度、第2分层厚度、第3 分层厚度和第m 分层厚度，m；d 为组合岩梁结构厚度，m。

2.3 等间距底锚巷道层状底板力学解析

运用力学理论推导出锚杆数n 为单数和偶数且等间距布置时组合岩梁结构的最大正应力σmax和剪应力τmax方程为：

n 为单数时：

n 为偶数时：

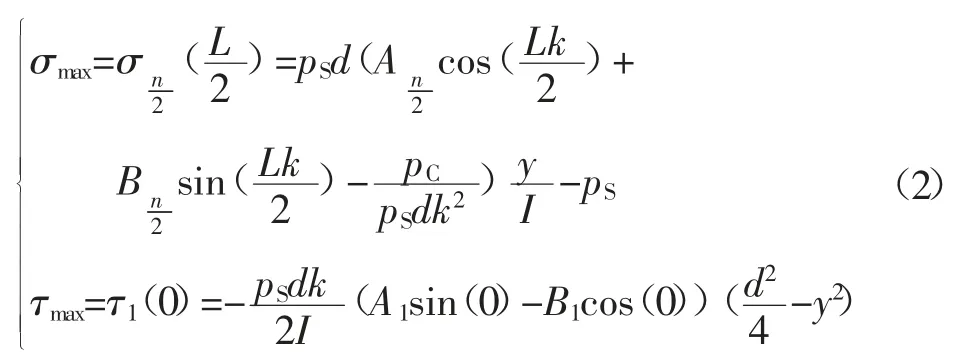
式中：cos（0）、sin（0）为组合岩梁结构左端位置，即x=0 时；k 为表达式代替字母为自变量；n 为锚杆根数；I 为组合岩梁结构惯性矩，m4；E为弹性模量；A1、B1为起始系数为组合岩梁结构中间位置力学方程系数。

任一分层正应力、剪应力与组合岩梁结构的正应力、剪应力满足如下关系：

由岩层破坏条件：

可得巷道层状底板任分层鼓起失稳的力学判别准则如下。

n 为单数：

n 为偶数：

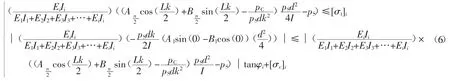
式中：E1I1+E2I2+E3I3+…+EiIi为第1 分层的抗弯刚度、第2 分层的抗弯刚度、第3 分层的抗弯刚度、…、第i 分层的抗弯刚度，MPa·m4；i=1、2、3、…、m；m为层状底板的层数；σi为第i 分层围岩的正应力，MPa；σ 为组合岩梁结构围岩的正应力，MPa；τi为第i 分层围岩的剪应力，MPa；τ 为组合岩梁结构围岩的剪应力，MPa；[σt]i为第i 分层抗拉强度设计值，MPa；[σc]i为第i 分层抗压强度设计值，MPa；φ 为围岩的内摩擦角；φi为第i 分层围岩的内摩擦角，（°）。

3 现场应用

借助已得出的力学判定准则对S6 采区2#回风上山层状底板第2 分层的稳定性进行判定。从矿井巷道围岩资料中获取模型基本参数的数值，数值包括：层状底板层数m=4；锚杆数n=3；巷道宽度4.5 m，底板跨度取L=8.5 m；第1 分层E1I1=288.8 MPa·m4、第2 分层E2I2=481.2 MPa·m4、第3 分层E3I3=373.8 MPa·m4和第4 分层E4I4=1 076.2 MPa·m4；第1 分层的厚度d1=0.54 m，第2 分层的厚度d2=0.67 m，第3 分层的厚度d3=0.42 m，第4 分层的厚度d4=0.81 m，组合梁结构的厚度，d=2.44 m；第2 分层抗拉强度设计值[σt]2=1.57 MPa；第2 分层抗压强度设计值[σc]2=36.7 MPa；第2 分层围岩内摩擦角φ2=29°；组合岩梁结构侧向水平应力为pS=7.23 MPa；底部所承受的均匀载荷pC=8.54 MPa；锚杆支护集中应力Fm=100 kN。

代入稳定性力学判定方程式（5），计算方程两边的值并进行判定，得：

由第2 分层中部上边界拉应力最大，计算得：[σt]2=1.57 MPa，1.09 MPa＜1.57 MPa，计算认为第2分层不会发生拉伸破坏。

由第2 分层的两端中性面位置剪应力最大，计算得：

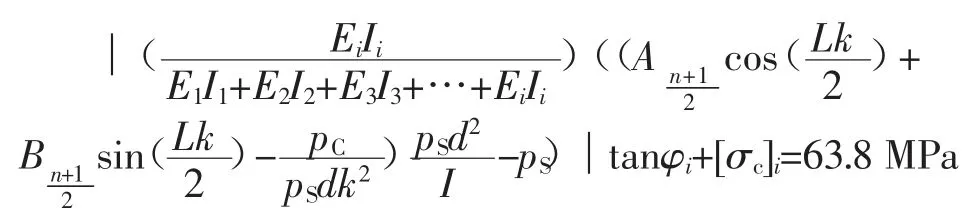
29.2 MPa＜63.8 MPa，计算认为第2 分层不会发生抗剪破坏。

根据以上等间距底锚巷道层状底板第2 分层鼓起失稳的判别，认为其结构稳定。

由此类推，可得第3 分层最先发生拉伸破坏，从而造成整体承载能力降低，锚杆不能有效地发挥其锚固效力，支护强度降低。

4 结 论

1）结合常村煤矿S6 采区2#回风上山，分析了层状底板压曲作用机理，建立了等间距底锚巷道层状底板力学模型。

2）运用力学理论分析等间距底锚巷道层状底板失稳力学机理，建立了等间距底锚巷道层状底板任分层鼓起失稳的力学判别准则。

3）借助构建的力学判别准则对S6 采区2#进行了反验与分析评价，揭示了最先发生破坏及导致支护体系失效的岩层，起到预判作用。此预判方法便捷、准确，可为层状底板支护方式、支护参数的选取提供一定的理论依据。