SDN动态停滞超时时间优化算法*
刘 霞, 杨桂芹, 邵军花, 蒋占军
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
0 引 言
随着互联网时代信息的爆炸式增长,云计算、大数据的产生,传统的网络结构已无法满足信息技术的要求。因此软件定义网络(software defined network, SDN)随之产生[1]。
SDN作为一种新兴的网络体系结构,将控制平面与转发平面解耦[2],交换机将控制器下发的配置信息存储到各自的流表中,由于交换机的流表空间资源有限,不能无限制地储存携带不同配置信息的不同流表项,当数据量庞大时,数据流类型会相应增加,会导致大量数据包涌入控制器的情况出现,降低SDN的性能及效率。
Zarek A等人在实际网络中测试分析,发现了流表项的停滞超时时间与流表资源利用率之间存在一定的关系[3],此后,研究人员开始陆续采用改进停滞超时时间的方式来对流表进行优化。Kim T等人用AR预测算法对下个取样周期内到达流进行预测,提出了一种动态调整流表项超时时间的方案[4];Zhu H等人提出了一种能够动态调整停滞超时时间的智能控制机制[5];付应辉等人提出了FDO算法,引入了资源偏好度,对停滞超时时间的设置进行了一定的改进[6];Zhang L等人借助排队论提出一种有效利用交换机资源的方案[7];唐菀等人通过对流表项工作机制的分析,提出了一种动静态流表项转换机制对停滞超时时间进行设置[8]。
上述方法都对SDN中的流表项超时时间进行了一定的研究,但均未考虑到根据网络实际负载,且相应算法复杂,在达到目的的同时增加了控制器负担。
因此,本文在前述工作的基础上,提出了一种动态停滞超时时间优化(dynamic timeout time optimization,DTO)算法,采用一种动态参数对流表项停滞超时时间进行动态调整,以期提升流表空间资源利用率、流表匹配率,提高SDN的性能。
1 算法分析
1.1 流表项停滞超时时间原理分析
在SDN交换机中,每个流表都由多条流表项组成,每个流表项对应一个特定的流,流表项通常由六部分组成,如图1所示。

图1 流表结构
流表项中的匹配域内储存着数据流的匹配信息,当新流进入流表后与各流表项的匹配域进行比对,当流表项在一定时间内无新流与之匹配时,该流表项将被清除出流表,这个设定值就称为停滞超时时间。
不同的停滞超时时间对于流表乃至整个网络的工作都有影响。若停滞超时时间设置过小,旧流表项会被频繁地移出流表,导致数据包进入流表时无法匹配到对应的流表项,发送packet-in数据包给控制器,占用控制器计算资源,降低网络性能,如图2(a)所示;而当停滞超时时间设置过大时,流表项在流表中的占用时间过长,导致新增流表项无法进入流表,降低了交换机的流表空间利用率,如图2(b)所示。

图2 停滞超时时间设置示意
从上述分析可见,在流表容量一定的条件下,可将各流表项设置合适的停滞超时时间来对流表进行优化。
1.2 DTO算法分析
1.2.1 动态指数平滑法预测算法分析
若要更精确地调整流表项停滞超时时间,必须预测下一时间周期内的新增流表项数量,本文在设计DTO算法时引入预测模块来提高设置精确度。传统的AR预测算法计算复杂度高,对控制器性能影响较大,综合考虑算法复杂度及预测精度,采用动态指数平滑DES法预测算法对下一时间周期内新增流表项数量进行预测。
通过对历史数据的收集,可得每个时间周期内流表新增流表项的数量,新增流表项可将其看作是时间序列,指数平滑法正是一种针对时间序列的预测方法,因此可运用在新增流表项的预测之中。加权则遵循“厚近薄远”的思想,即距离预测时刻越近的时间周期内的数据所占的权重越大,因此,准确地把握临近时间周期的历史数据,同时又不至于被异常数据影响过大,可提高预测准确度。
设{Xt}为新增流表项观测值的序列,则一次指数平滑值的计算公式[9~11]为
Ft=αXt+(1-α)Yt-1
(1)
式中F0称为初始平滑值,Ft为t时刻的平滑值,α为平滑系数,满足0<α<1。而一次指数平滑模型的预测值为
(2)
为尽可能减小预测误差,本文采用二次指数平滑法预测新增流表项数量。在一次指数平滑的基础上再次进行指数平滑,其平滑值计算方法为[12,13]
(3)
则对时间序列建立的预测模型为
(4)
(5)
此外,为解决平滑初始值F0以及平滑参数α难以确定的缺点,引入了参数μt,对应不同时刻的观测值序列{Xt},有不同的取值与之对应,令
(6)
可见,μt为t的函数,且当0<α<1,t>1时,0<μt<1,满足平滑参数的要求。当t=1时,有
(7)
则可令初始状态值为μt=1,μt为时间序列{Xt}的动态平滑参数。因此,{Xt}序列以μt为动态平滑参数的动态指数平滑法预测模型为
(8)

取动态参数μt是为了依据不同情况得到更准确的预测值,但动态的μt依然要依赖于一个固定的α,而α的取值应根据预测误差的平方SSE(均方差)做出变化,以均方差最小为目标建立α的优化模型,如下式
(10)
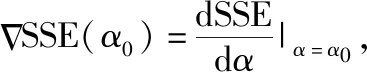
1.2.2 流表项停滞超时时间优化算法分析
以往的算法对于数据量时刻变化的网络并不适用,为解决这一缺点,DTO算法考虑当前网络中的实际负载,引入了动态参数,根据网络负载变化做动态停滞超时时间优化。
从整体结构上讲,流表容量可表示为Nmax=Nc+Ne,Nc为取样周期为T时刻的实际流表项数量,Ne为取样周期为T时刻的空余流表项数量。通过对历史数据的分析预测到下一时刻将会进入流表的新增流表项的数量,记为y,当y
(11)
式中tori为流表项的初始停滞超时时间,而tmod为经过调整后的停滞超时时间。上式表示当y
1.3 DTO算法
综合上述分析,本文所提出的DTO算法分为2个模块,模块1为新增流表项数量预测模块,它为整个算法提供了数据基础,首先收集历史时刻的流表项数量的实测序列,而后利用动态指数平滑(DES)模型得到下一时间周期的新增流表项数量的预测值,至此模块1的工作完成。而模块2利用该预测值与网络当时的负载状况,采用动态参数对流表项停滞超时时间进行优化调整后,输出新流表。
DTO整体算法实现过程如下:
模块1:
1)收集历史新增流表项数量数据;
2)DES算法计算出估计值;
模块2:

6)若p>1,tmod=tori,否则tmod=p*tori;
7)此时各流表项的超时停滞时间为ti(i=1,2,3,…,Nc),若ti=0,则将此流表项清除出流表,否则令ti=tmod;
8)输出调整后的流表。
2 结果与分析
本文采用SDN常用仿真软件Mininet搭建实验环境,在主机上的VMware workstation中安装Ubantu14.04LTS虚拟机,并在其中安装Mininet和Ryu控制器。OpenFlow 交换机以及主机都用Mininet模拟实现,并用sFlow对整个网络进行流量监控及数据分析。
实验中指定交换机中的数据流最多有105条且呈波动状态,交换机的流表总容量为300,流类别为990,本文将通过平均吞吐量、流表资源利用率、流表匹配率3个指标对DES算法效果进行验证,同时与不使用流表优化算法的初始网络、传统AR算法的优化网络以及FDO算法的优化网络3种情况下的各指标进行比较。
2.1 流表匹配率分析
本文提出的DTO算法的直接效果是尽可能多地使进入流表的数据流能够与流表项成功匹配,因此,流表匹配率的大小直接反映了优化效果。图3(a)所示为流表匹配率的实验结果。
随数据流数量的增加,流表匹配率呈现先下降后稳定的状态。开始时由于数据量以及流类别未超过流表容量,4种网络下流表匹配率均接近100 %。随着数据量大幅增加,初始网络的流表匹配率急剧降低,当数据量超过5 000时,匹配率基本稳定在65 %左右;而优化后的3种网络虽然也有下降,但幅度不大。在同样的网络条件下,数据量超过4 000时,AR算法与FDO算法优化网络的流表匹配率在83 %左右浮动,DTO算法由于添加了动态调整参数,流表匹配率在86 %左右浮动,优化效果明显。
2.2 流表资源利用率分析
流表资源利用率可以反映交换机流表空间的利用状况,若流表资源利用率低则表示流表空间未充分使用即交换机性能低。图3(b)为4种网络下的流表资源利用率曲线。
从整体上看,4条曲线均为先增大后平稳的状况。在网络中数据量较少时,4种网络下的流表资源均未得到充分利用。随着数据量的增大,流表资源利用率提高;当网络中的数据量持续增加时,4种情况下的流表资源利用率均达到了基本稳定状态,这是由于SDN的转发机制导致交换机在大数据量的情况下只能等待控制器配置流表项,出现了性能瓶颈。但从图中可明显看出优化后的三种网络利用率远高于未使用优化算法的初始网络,AR算法与FDO算法的流表利用率均维持在76 %左右,而本文提出的DTO算法优化方案对流表项利用率的提升稳定在78 %左右,优于其他两种算法。
2.3 网络平均吞吐量分析
当数据量增大时,由于交换机处理能力的不足,会限制网络的平均吞吐量,使其达到瓶颈。因此,本文算法对于交换机性能的提升也将会对同时提高网络平均吞吐量。实验结果如图3(c)所示。
在数据流数量较小时,4种网络的吞吐量均在增加;但随着网络中的数据量的逐步增大,初始网络的吞吐量明显到达了其瓶颈,且略有下降趋势。而传统AR算法的优化网络对这一现象略有改善,但是在数据量超过8 000时也呈现出下降趋势,这是由于AR算法虽然对交换机的性能有所改善,使得吞吐量有了短暂的提升,但是其算法的复杂度增加了控制器的负担,当数据量不断增加时,控制器的性能限制了其整体的网络性能。从曲线走势可以看出,FDO算法与本文的DTO算法优化网络的吞吐量都在不断提升且最终达到了稳定状态,并未出现大幅度下降趋势,但DTO算法的优化效果明显强于FDO算法的优化效果,本文的DTO算法吞吐量最终达到了75 MbPs左右,而FDO算法只达到了72 MbPs,可见,在同样的网络状况下,采用DTO算法进行优化的网络吞吐量明显高于其他三种网络并能够保持稳定。

图3 仿真结果
综合以上实验结果,对于数据流数量大的SDN,3种优化网络相比未优化的初始网络对于网络性能的提升是显而易见的。另外,相比于传统的AR算法和FDO算法,本文的优化算法达到了相对较高的流表匹配率、流表资源利用率以及网络平均吞吐量,而这3个参数分别直观地体现了算法的直接效果、交换机的性能以及整个SDN的性能,因此本文的优化算法实现了更佳的优化目的。
3 结 论
通过仿真验证与分析可知,在同样的网络下,DTO算法相比于初始网络以及其他两种优化算法能有效地提高流表资源利用、流表项的匹配率,提升网络的整体性能。但在设计方案时未考虑每个流表项使用频率不同这一因素,后续将继续改进算法,依据频率高低,对不同的流表项做出不同的处理。

