优化BP网络在农业墒情站数据预测中的应用研究

杨倩 严凯 姚凯学 何勇

摘 要：针对农业墒情站在采集农作物生长环境因子时表现不可靠的问题，文中使用BP神经网络来预测环境数据，辅助墒情站，为农户提供有效数据，从而对农作物进行更精准地保护。由于BP存在网络结构难以确定等问题，故利用自适应加速因子的粒子群算法、可改变搜索空间的蜂群算法和自适应变异概率的遗传算法三种方法来优化BP的初始权阈值。经仿真证明，三种改进方案不仅提高了BP预测的收敛速度，而且提高了预测精度。自适应加速因子的粒子群BP模型预测效果最佳，故将其嵌入农业墒情站，目前，墒情站已经投入使用，可有效保护农作物。

关键词：农业墒情站;神经网络;遗传算法;粒子群算法;蜂群算法;预测模型

中图分类号：TP183;TP273文献标识码：A文章编号：2095-1302（2019）08-00-05

0 引 言

农业数字化和精准化是现代农业的核心技术，农业环境监测显得格外重要。农业墒情站集成了诸多传感器，主要检测光照、大气温湿度、土壤温湿度、雨量、雨速、风速、海拔等环境因子。只有当各个环境因子均满足农作物生长的要求时，才能使农作物更好地生长。环境因子数据是否可靠成为农业墒情站是否有效的决定因素，为了提高传感器数据的可靠性，引入BP预测模型。由于BP存在收敛速度慢、易陷入局部极小等问题[1]，因此本文建立I3GA-BP预测模型、I2ABC-BP预测模型和I1PSO-BP预测模型，并且I1PSO-BP预测模型已经成功嵌入到后台，运行良好。

1 农业墒情站

基于STM32F103ZET6的茶园墒情站总体框架如图1所示。系统由数据处理模块、太阳能供电模块、传感器（空气温湿度、土壤温度、光照、雨量、雨速、土壤水分、土壤pH等）、远程PC端（集成了优化的BP模块）、手机端等部分构成。

2 PSO优化BP神经网络

粒子群算法与模拟退火算法相似，其基本思想是从随机解出发，通过迭代寻找最优解，粒子的品质是通过适应度来评价[2]。它比遗传算法规则简单，没有遗传算法的解码、交叉和变异操作，具有收敛速度快、精度高、易实现等优点[3]。

2.1 PSO算法

假设在一个D维搜索空间（D根据具体问题而定），一个群体由n个粒子组成，第i个粒子的位置向量为POPi=（POPi1，POPi2，…，POPiD），速度向量为Vi=（Vi1，Vi2，…，ViD），其中i=1，2，…，n。i粒子的历史最优位置为Pbesti=（Pbesti1，Pbesti2，…，PbestiD），整个群体最优位置为Gbesti=（Gbesti1，Gbesti2，…，GbestiD）。粒子的位置和速度更新公式

如下：

式中：d=1，2，…，D;r1和r2为[0，1]上的随机数;c1为粒子自身学习的认识，称为“认知”因子;c2为粒子对整个种群学习的认识，称为“社会”因子;wmax为最大权重;wmin为最小权重;t为当前迭代次数;tmax为最大迭代次数。

2.2 PSO算法的改进

通常将加速因子c1和c2设置为常数2，c1是个体自身学习的能力，c2是粒子间协作学习的能力。迭代寻优是非线性变化过程，固定的加速因子无法体现此种变化。在迭代初期，粒子期望在较短时间内能发挥自身的优势，快速搜索到最优值;在迭代后期，粒子期望能抓紧粒子间协作，快速收敛到最优解。本文将c2设成非线性递增函数，将c1设成非线性递减函数，公式如下：

2.3 改进的PSO优化BP预测模型求解思路

PSO某代的某个粒子的位置向量的维数（D）为BP权值阈值的总数，向量POP为BP权值W和阈值θ的集合。粒子i的适应度fitnessi的表达式为

式中：N为样本数;M为输出层节点数;yji为实际输出值;y'ji为期望输出值。

本文给出的PSO优化BP的步骤如下：

（1）构建PSO-BP网络，初始化BP;

（2）初始化粒子群算法，有编码长度、种群大小、速度范围、位置范围、迭代次数等;

（3）计算各个粒子的Pbest，选择种群最优粒子作为Gbest;

（4）计算本次迭代各个粒子的适应度值，如果当前粒子的Pbest优于当前粒子的历史Pbest，则更新粒子的位置信息和Pbest。如果本次迭代所有个体的Pbest有优于Gbest，则更新Gbest;

（5）更新加速因子c1，c2，粒子的位置和速度信息等;

（6）达到最大迭代次数，将Gbest的D维信息依次赋值给BP神经网络的权值和阈值，开始预测，否则转步骤（3）。

2.4 改进的PSO优化BP的预测模型在农业墒情站中的应用

根据试凑法将BP输入层、隐藏层、输出层节点数设置为7，12，1。最大训练次数为1 000，精度定为0.000 01，学习速率的初始值为0.1，隐藏层传递函数为tansig，输出层传递函数为purelin，训练函数为trainlm，期望误差为均方误差函数MSE。粒子群算法种群大小为50，编码长度为109，速度范围[-1，1]，种群个体范围[-3，3]，c1和c2初始值均为

1.494 45，最大進化代数为100。将光照强度、大气温度、大气湿度、风速、土壤湿度、雨量、前1 h的平均土壤温度作为网络的7个输入，后1 h的土壤温度作为输出。训练数据为2016-07-22—2016-10-01的1 656组数据，测试数据为2017-07-25—29的100组数据。

改进后的PSO优化BP的迭代适应度值如图2所示，可看出迭代10代以内就能获得比较优良的个体。改进后的PSO优化BP的预测输出和输出相对误差如图3、图4所示，可看出改进后的PSO优化BP的预测相对误差最大为3.9%，最小为0.2%，平均为3.06%，用时21.706 6 s;而BP的预测相对误差最大为38%，最小为6%，平均为9.67%，用时8.321 9 s。

3 ABC优化BP神经网络

人工蜂群算法通过特有角色分工机制提升人工蜂个体的局部寻优能力，最终使得全局最优值凸显，有良好的收敛速度[4]。蜂群模型有三个要素，即蜜源（问题的可行解）、被雇佣的蜜蜂（采蜜蜂）和未被雇佣的蜜蜂（侦查蜂、跟随蜂）。其中，采蜜蜂维持种群优良解，跟随蜂提高种群收敛速度，侦查蜂摆脱局部最优[5-6]。

3.1 ABC算法

假设在一个D维搜索空间（D根据具体问题而定），蜜源i（i=1，2，…，NP）的质量适应度为fiti，第t次迭代过程中第i个粒子的蜜源位置为Xti=（Xti1，Xti2，…，XtiD）。其中，NP为蜜源的个数;XtiD∈[Ub，Lb]，Ub和Lb分别为解的上限和下限。采蜜蜂（即引领蜂）根据式（6）随机产生初始群体。

搜索开始，根据式（7）在蜜源i周围更新蜜源位置。

式中：D为随机整数;k为采蜜蜂在当代群体中选择一个非i的蜜源号，k∈[1，NP]且k≠i;φ为[-1，1]的均匀随机数。当新蜜源X'iD的适应度优于XiD时，采用贪婪选择法以新蜜源代替旧蜜源;否则，保持XiD不变。待所有采蜜蜂完成任务后回到信息区与跟随蜂分享蜜源，跟随蜂根据概率Pi以及轮盘赌来跟随采蜜蜂，当Pi大于均匀随机分布数r时，以采蜜蜂相同的更新策略来进行选择更新。Pi见式（8），fiti与fitnessi是一样的。

当采蜜蜂和跟随蜂完成迭代任务以后，如果蜜源Xi有trial次未更新且trial大于limit，则侦查蜂出现并根据式（6）随机产生一个新的蜜源代替Xi。

3.2 ABC算法的改进

在函数中引入惯性权重，通过惯性权重W（i）来控制采蜜蜂和跟随蜂的搜索空间，公式如下：

式中：w（t）=wmin+t（wmax-wmin）/tmax;t為当前迭代数;tmax为最大迭代数;wmax为最大权重;wmin为最小权重。随着迭代次数的增加，w（t）可调控搜索范围以提高算法的精度和收敛效率。在迭代初期，蜜源信息相对小，小的惯性可以抓住最优解的可能域，随着优良解的陆续出现，后期较大的惯性可以提高算法的全局搜索能力，发现更多优良解。

3.3 改进的ABC优化BP的预测模型求解思路

ABC某代的某个蜜源的位置向量的维数（D）为权值阈值的总数，向量Xi为BP权值W和阈值θ的集合。

本文给出的ABC优化BP的步骤如下：

（1）构建ABC-BP网络，初始化BP;

（2）初始化蜂群算法，有蜜源个数及大小、更新失败次数、位置范围、迭代次数等;

（3）采蜜蜂搜索蜜源Xi，计算其适应度并用贪婪算法更新原蜜源;

（4）计算概率，跟随蜂依据概率和轮盘赌方法选择采蜜蜂，根据采蜜蜂更新原则进行更新;

（5）根据采蜜蜂和跟随蜂两种蜜蜂的蜜源的未更新次数来判断是否转化成侦查蜂，如果蜜源为更新次数大于规定的次数，则侦查蜂随机搜索新蜜源;

（6）记录最好蜜源;

（7）判断是否达到终止条件，如果达到，将最好蜜源的D维信息依次赋值给BP神经网络的权值和阈值，开始预测，否则转步骤（3）。

3.4 改进的ABC优化BP的预测模型在农业墒情站中的应用

根据实验，发现四层的ABC-BP神经网络有较好的预测精度，三层的预测精度仅略高于单纯的BP网络，故将BP输入层、第一层隐藏层、第二层隐藏层、输出层节点数设置为7，15，15，1，BP其他设置如PSO-BP模型的设置。蜂群算法的蜜源数为80，蜜源维数为376，最大失败次数为30，最大进化代数（因ABC算法复杂，特将进化代数调小）为50，Ub=3，Lb=-3。

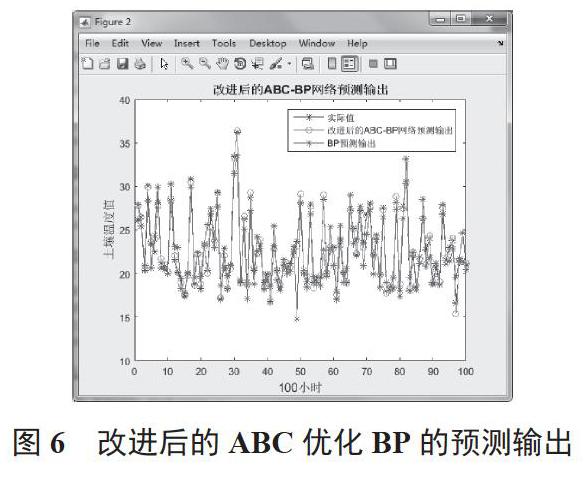
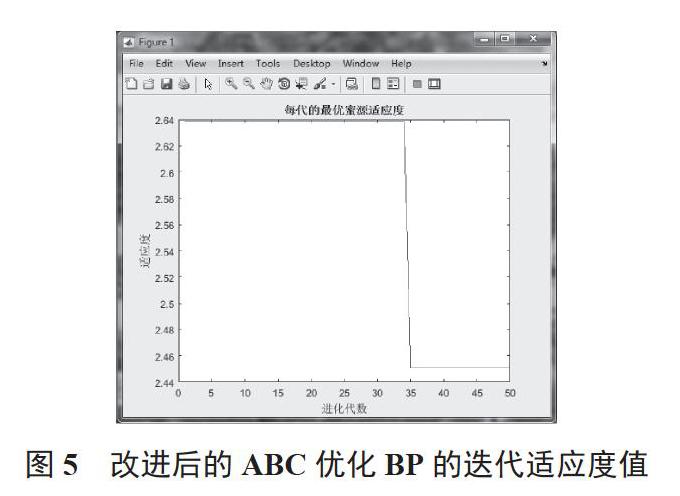
改进后的ABC优化BP的迭代适应度值如图5所示，可看出30多代可获得较优良个体。改进后的ABC优化BP的预测输出和输出相对误差如图6、图7所示，可看出改进后的ABC优化BP的预测相对误差最大为4.2%，最小为0.5%，平均为3.27%，模型用时167.892 1 s。

图5 改进后的ABC优化BP的迭代适应度值

图6 改进后的ABC优化BP的预测输出

图7 改进后的ABC优化BP的相对误差

4 GA优化BP神经网络

遗传算法（GA）是基于空间的搜索算法，直接对研究对象的编码进行操作，通过问题域中的目标函数（适应度）的大小对个体进行评价，对个体进行选择、交叉和变异，生成新种群，具有较强的鲁棒性和较高的并行性[7-8]。

4.1 GA算法的改进

遗传算法经常出现过早收敛的现象，变异操作虽然保证了进化的搜索功能，但其随机性可能会破坏优良个体，降低种群的平均适应度值，故对变异算子进行改进，使其随迭代自适应变化[9-10]，变异公式如下：

式中：Pm为本代变异概率;Pmax和Pmin分别为上一代最大、最小变异概率;Fa为当前个体的适应度值;Fmax和Fmin分别为上一代最大最小适应度值;Favg为上一代平均适应度值。当种群的个体适应度值普遍较好时，此时应该降低变异概率，使得优良的个体可以大部分被传递给下一代;当种群的个体适应度值普遍较差时，此时应该提高变异概率，使得劣质的个体可以大幅度变异，产生新个体，寻找优良个体，提高收敛速度。

4.2 改进的GA优化BP的预测模型求解思路

GA某代的某个个体编码长度为权值阈值的总数，本文GA优化BP的步骤如下：

（1）构建GA-BP网络，初始化BP;

（2）初始化遗传算法，有种群大小、编码长度、交叉率、变异率、编码方式、迭代次数等，其中编码长度由输入层与隐藏层权值、隐藏层与输出层权值、隐藏层阈值、输出层阈值四部分组成;

（3）对当代种群个体分别进行适应度评价;

（4）选择操作，可采用轮盘赌法、随机遍历抽样法等，本文采用适应度比例方法选择个体;

（5）交叉操作，可采用实值重组、二进制交叉，本文采用实数编码加实值重组;

（6）变异操作，可采用实值变异、二进制变异，本文采用实值变异;

（7）判断是否达到终止条件，如果达到，将最好个体赋值给BP神经网络的权值和阈值，开始预测，否则转步骤（3）。

4.3 改进的GA优化BP的预测模型在农业墒情站中的应用

BP设置如PSO-BP模型的设置，遗传算法种群大小为50，编码长度为109，编码范围为[-3，3]，种群数为50，最大进化代数为100，交叉概率为0.9，初始变异率为0.3，最大为0.4，最小为0.1。

其中，实值交叉操作是选择几对（两两一对）染色体，选择它们的串的局部进行交叉;实值变异操作是选择几个染色体，对他们的局部进行随机数赋值。选择操作中的适应度比例选择法的个体选择概率为：

式中：Fi为第i个个体的适应度值;k为系数;N为种群个数。

改进后的GA优化BP的迭代适应度值如图8所示，可看出迭代50多代就能获得比较优良的个体。改进后的GA优化BP的预测输出和输出相对误差如图9、图10所示，可看出改进后的GA优化BP的预测相对误差最大为17.3%，最小为0.8%，平均为5.39%，用时46.529 1 s。

5 多种优化BP神经网络的数据预测模型实验结果

为了验证多种墒情站数据预测模型的优良性能，本文分别对BP算法、PSO-BP算法、改进后的PSO优化BP算法（I1PSO-BP）、ABC-BP算法、改进后的ABC优化BP算法（I2ABC-BP）、GA-BP算法、改进后的GA优化BP算

法（I3GA-BP）这7个模型进行相同条件下的实验，记录数据并进行比较。

表1列出了7种模型误差和耗时的比较，发现PSO算法相对于ABC算法和GA算法收敛速度明显加快;PSO算法的两种模型和ABC算法的两种模型预测准确率相近且较高;BP模型和GA算法的两种模型预测准确率较低。考虑到农业墒情站数据的准确性和时效性，最终决定将改进的PSO优化BP算法作为农业墒情站数据预测模型。

6 结 语

本文提出多种预测模型，经过实验，结果表明，在一定条件下，改进后的粒子群算法优化BP模型具有较高的预测准确率和较低的时间消耗。预测模型已经嵌入墒情站系统，在贵州大学农学院植物研究实验基地、瓮安茶园和贵州师范学院等地已经投入使用，可以有效指导农业研究和生产。

参 考 文 献

[1]孔红山，郁滨.一种基于 BP 神经网络的 VIRE 改进算法研究[J].系统仿真学报，2018，30（9）：3586-3595.

[2]李婕，白志宏，于瑞云，等.基于PSO优化的移动位置隐私保护算法[J].计算机学报，2018，41（5）：1037-1051.

[3]陈建明.基于遗传算法的粒子群算法的参数分析[D].北京：中国地质大学，2012.

[4]李楠，朱秀芳，潘耀忠，等.人工蜂群算法优化的SVM遥感影像分类[J].遥感学报，2018，22（4）：559-569.

[5]于佐軍，秦欢.基于改进蜂群算法的K-means算法[J].控制与决策，2018，33（1）：181-185.

[6]王志刚，尚旭东，夏慧明，等.多搜索策略协同进化的人工蜂群算法[J].控制与决策，2018，33（2）：235-241.

[7]徐小钧，马利华，艾国祥.基于多目标遗传算法的多星座选星方法[J].上海交通大学学报，2017，51（12）：1520-1528.

[8]吐松江·卡日，高文胜，张紫薇，等.基于支持向量机和遗传算法的变压器故障诊断[J]. 清华大学学报（自然科学版），2018， 58（7）：623-629.

[9]季慧，金银富，尹振宇，等.遗传算法改进及其在岩土参数反分析中的应用[J].计算力学学报，2018，35（2）：224-229.

[10]肖海蓉，李惠先.基于自适应遗传算法的网格任务调度优化[J].吉林大学学报（理学版），2015，53（2）：297-301.