降低护坦式消力池深度计算的新方法

王馨梅，张小艳

(甘肃农业大学水利水电工程学院，甘肃 兰州 730070)

1 降低护坦式消力池深度计算现状

底流消能又称为水跃消能，是在泄水建筑物下游设置消力池，控制水跃发生的位置，通过水跃产生的表面旋滚和强烈紊动来达到消能的目的，由于高速水流的主流在底部，所以称为底流消能[1]。

底流消能工程措施有：降低护坦高程，增加下游水深，形成降低护坦式消力池；或在护坦末端建消力坎，以抬高尾水，形成坎式消力池；或既有降低护坦，又有消力坎的综合式消力池[2]。本文主要研究降低护坦式消力池深度的计算方法。

目前降低护坦式消力池深度的计算方法主要有传统试算方法、简化计算方法和其他计算方法。

1.1 传统试算方法

设跃前断面水深为h1，跃后断面水深为h2，通过溢流坝的单宽流量q，下游水深为ht，下游河床以上总水头为E0，消力池的深度为d，传统方法计算消力池深度的公式为[1]：

d=σjh2-ht-Δz

(1)

(2)

(3)

(4)

式中，q—单宽流量；h2—护坦高程降低后收缩断面水深h1的跃后共轭水深；σj=1.05；ht—下游河床水深；d—消力池深度；池末水深hT=σjh2；φ′—消力池的流速系数，一般取φ′=0.95。

当E0、q、φ、φ′、ht已知时，即可用式(1)、(2)、(3)和(4)联立求解消力池深度d，一般需要试算法。试算法计算消力池深度时，先假定一个消力池的深度d，代入式(2)求跃前断面水深h1，由式(3)求h2，由式(4)求Δz，然后再代入式(1)求d，如果求得的d与假设的d相同，消力池深度即为所求。试算法需多次应用以上公式反复计算才能完成。传统试算方法虽然比较麻烦，但方法成熟，计算结果可靠。我国现有的水力学、水工建筑物教材以及溢洪道设计规范均采用传统计算方法。

1.2 简化计算方法

简化计算方法，也称为表解法[3]，是根据某种函数关系，事先做成表格，在计算时查用，表解法不是一步完成的，也有一个试算过程，即将试算变成查表，简化计算方法检验的条件为：

(ht+d)/h2=1.02～1.1

1.3 图解法

文献[4]给出了消力池深度计算的图解法，该图解法将传统试算方法的参数改为无量纲参数，得出了计算跃前断面水深、跃后断面水深以及消力池深度的图示方法，用该方法可以比较简单的计算出消力池的深度，但图解法计算精度较低。

1.4 其他计算方法

近几年来，对消力池深度的计算还有一些新的方法，文献[5]通过对传统计算方法的简化，提出了计算消力池深度的新公式，即

(5)

式中，hk—临界水深；Fr—跃前断面弗劳德数。

式(5)看似简单，实际上跃前断面的Fr仍然是消力池深度的隐函数关系，计算Fr仍需试算，为此文献[5]拟合了Fr和参变量Z的关系，其中Z的表达式为：

(6)

Fr=kZx+c

k=3.8-1.755/φ

x=0.1φ+0.585

c=1.61φ4-0.065

文献[5]认为在Fr较大时计算误差不大，但在Fr<2.5时需将计算结果适当提高1%～3%。以上公式适应的条件为Fr=2～9。

文献[3]利用升坎的受控水跃，通过动量方程求解池深的公式为：

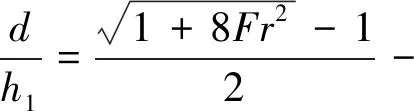
(7)

式(7)亦表明，消力池深度是跃前断面Fr的函数。

文献[6]给出了共轭水深和消力池深度的公式为：

(8)

以上是目前降低护坦式消力池深度计算的一些方法，可以看出，不管是那种方法，消力池深度的计算都与跃前断面、跃后断面水深有关，而跃前断面水深又是消力池深度的函数，所以在计算时均需进行试算。

文献[7]～[10]都对消力池深度传统计算方法编制过电算程序，以使计算过程简单。

2 降低护坦式消力池深度计算的比较

某溢流坝[11]已知坝顶高程为110.0m，溢流坝面长度中等，河床高程为100.0m，上游水位为112.96m，下游水位为104.00m，通过溢流坝的单宽流量q=11.3m3/(s·m)，溢流坝的流速系数φ=0.95，试判别坝下游是否要做消能工。如果要做消能工，试计算降低护坦式的消力池的深度。

2.1 传统试算方法

通过试算，坝下游出现远离水跃，需设消能工，并计算出降低护坦式消力池的深度为1.688m。

2.2 简化计算方法

根据文献[3]给出的表解法，通过查表计算得当(ht+d)/h2=1.02时消力池的深度为1.8m。

根据文献[5]公式求得x=0.68，c=1.238，k=1.953，hk=2.353，Z=3.718，Fr=6.007，消力池深度d=1.95m。

由式(7)试算求得消力池深度d=1.955m。

前述传统试算方法理论推导严密，精度高，因此以传统试算方法为标准，简化计算方法的误差为6.63%；文献[5]的误差为15.52%；式(7)的误差为15.82%。可以看出，不同的公式得出的计算结果差异较大，所以寻求新的计算方法是完全必要的。

3 用动量方程推求新公式

消力池深度推导简图如图1所示，1- 1断面和2- 2断面的动量方程为：

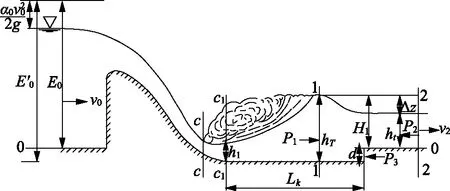
图1 消力池深度推导简图

(9)

v1=q/(σjh2)v2=q/ht

(10)

将式(10)代入式(9)整理得

(11)

式(11)即为由动量方程得到的消力池深度计算的新公式。由于消力池的深度小于跃后水深，所以根号前取负号。

溢流坝收缩断面水深为：

(12)

由式(12)得

(13)

由水跃方程知

(14)

式(11)实际上仍是一个隐函数，这是因为跃后水深h2未知、而h2与跃前水深hc和消力池的深度d有关，所以在计算时仍需要试算。为了简化计算，下面推导消力池深度的迭代计算公式。

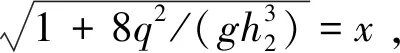
(15)

将式(15)代入式(14)得

(16)

将式(16)代入式(13)得

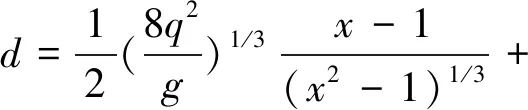
(17)

将式(15)代入式(11)得

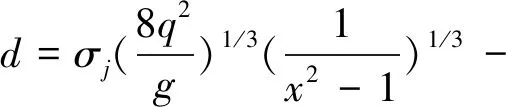
(18)

由式(17)和(18)得

(19)

式中

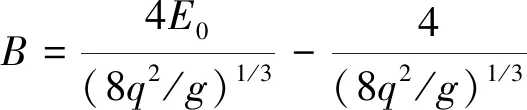
(20)

式中，φ、σj、q、E0、ht、g已知，代入式(19)迭代出x，将x代入式(15)、(16)和公式(17)或(18)求出跃后和跃前水深h2、h1以及消力池深度d。

用新公式求解图1消力池深度d。

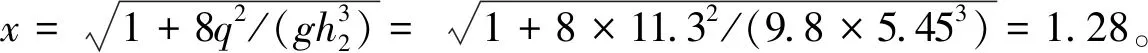
用传统试算方法求得消力池深度为1.688m，与本方法相比非常接近，误差仅为0.6%。

比较传统的试算方法和本文的新公式计算方法，两者均是通过严密的理论推导得到的，计算结果非常相近，进一步论证了传统方法计算的正确性，同时也说明新公式计算结果正确，且不需要试算。

4 结语

本文分析了降低护坦式消力池深度的研究现状，比较了各计算公式的精度，比较认为：传统的降低护坦式消力池深度的计算方法严谨、计算精度高，为各国水利工程所采用。本文还通过动量方程提出了计算降低护坦式消力池深度的新方法，经验证，该方法与传统方法计算结果非常吻合，且避免了传统方法试算的困难，可以作为工程设计采用。