基于ANSYS Workbench的压接修理民机液压管路振动特性分析

贾宝惠，于灵杰，卢翔

中国民航大学 航空工程学院，天津 300300

飞机运行时会受到各种激振力作用，继而产生剧烈振动，当激振力频率接近于液压管道的固有频率时则会产生共振，最终液压管路发生断裂破坏[1]。而损伤管路最常见的维修方式为压接修理，因此有必要对压接修理民机液压管路进行强度评估和振动特性分析。

国内外学者采用了不同方法深入研究了输液管路的动力学特性，酒井敏之[2]和Benson[3]等对管路的流固耦合振动问题进行研究，并分析减少管路振动方面的问题；Tornabene等[4]运用广义微分求积法对输液直管的流速进行计算分析；Ritto等[5]提出了具有不确定性随机结构的输流管道模型，同时对其动态稳定性进行分析；Tubaldi等[6]研究了具有弹性边界条件的圆柱壳，并对其非线性振动问题进行探究；杨大伟等[7]建立输液管路的有限元模型，全面分析了流固耦合作用对管路振动特性的影响；王海林等[8]推导出基于流固耦合法的管路运动方程，证明流固耦合作用可降低管道与液体的固有频率；陆春月等[9]建立了管路流固耦合振动数学模型，并对管路振动进行有限元仿真和试验验证，结果表明：管路的流固耦合振动能受变频系统的控制，属于简谐振动；Huang等[10]对两端支承输液直管的固有频率和稳定性进行研究；Wang等[11]建立输液管路的三维流固耦合动力学模型，分别计算出直管和曲管的固有频率；沈旻昊[12]在ANSYS软件中建立了某试验管路的简化模型，用等效质量法对管路进行模态分析，并用流固耦合法完成了管路在简谐激励下的瞬态响应分析；韩晓辉[13]分别对液压管路的流固耦合数值分析和有限元仿真进行研究，并对典型飞机液压管路进行振动特性分析和共振疲劳试验研究；李帅军等[14]的研究表明分支管的角度和位置的变化对管内流体压力波的影响大于对管道结构振动的影响；安晨亮等[15]建立了摩擦作用下管路流固耦合振动的传递矩阵方程，分别研究了两端固支液压直管和飞机翼尖弯曲管路的流固耦合振动特性。

国内外专家大多针对输流管路的理论模型与仿真模拟进行研究，尚未涉及到修理后管路的振动特性问题。压接修理是将飞机上液压管路的损伤部分切除，采用与其相同材料的标准接头，将切除后的两段管路采用压接方式连在一起[16]。

由A320飞机维护手册[17]知待压接管路的每端允许有公差，标准接头最大允许公差为7.6 mm，特殊接头ABS0478最大允许公差为20.0 mm。

本文研究对象为MS21902标准接头，故压制区域最大允许公差为7.6 mm。当民机液压管路的规格为1/4 in(1 in=0.025 m)时，压接修理所需的压接管内径为6.6 mm，外径为8.59 mm，压接长度范围为38.86～39.14 mm。

本文基于试验与仿真相结合的方法，对压接修理民机液压直管进行振动特性分析。首先分别对一段压接修理民机液压直管进行扫频振动试验和有限元仿真计算，对比其前6阶固有频率，验证对压接修理民机直管进行有限元建模与仿真的合理性；然后对压接修理民机液压直管进行受力分析，找出其产生最大应力与变形的区域；最后分别以压接长度和压制区域公差为变量建立压接修理民机液压直管有限元模型，通过分析其振动响应，得出民机液压直管的最佳压接修理参数，并将其响应云图与受力分析结果进行对比，证明该压接修理参数的合理性，为制定民机液压直管的压接修理方案提供理论依据。

1 压接修理民机液压直管的振动试验

1.1 试验设备与环境

一个典型的系统包括：振动台、功率放大器、数据采集系统、冷却系统和振动控制仪。图1为振动试验的系统框图。

在标准大气压下利用手摇泵对待测管路加油加压，进行扫频振动试验，最后利用东华测试信号采集仪进行信号采集并分析数据，试验设备如表1 所示。

图1 振动试验系统框图Fig.1 Block diagram of vibration test system

表1 试验设备Table 1 Test equipment

序号试验设备1三综合振动台2加速度传感器3东华信号采集仪4手摇泵

1.2 振动试验

试验对象为一段压接修理民机液压直管，管路材料为不锈钢，外径为6.5 mm，厚度为0.41 mm，管路原始长度为700 mm。将上述直管截成前半段300 mm、后半段400 mm的2段，用长为38.86 mm的压接管将2段直管压接到一起，其中压制区域公差为4 mm，压接过盈量为0.1 mm。

开始振动试验，具体步骤如下：

1) 选取一段压接修理民机液压直管试件并灌入液压油，将管路密封使其接头处不漏油。

2) 将试验工装固定于振动台的上表面，并将管路试件依照两点约束的方式固定于试验工装上，并保证试件是无应力安装。

3) 在管路接头区域粘上一个IEPE压电式加速度传感器，主要是对径向加速度响应进行测量，将加速度传感器另一端与东华信号采集仪连接并调试仪器。

4) 在试验工装上粘上另一个加速度传感器，将加速度传感器与振动控制仪连接作为控制用。在振动控制软件上设置振动试验基本参数，其中最低下限频率为5 Hz，最高上限频率为2 000 Hz(一般来说民机在正常飞行时受到的激振力频率可达2 000 Hz)；通道参数中传感器为加速度传感器，其类型设置为电荷；正弦扫频控制参数中最大自检电压为0.5 V(试验中可适当调节，最大不超过10 V)，扫频试验从低频开始扫到高频。

5) 试验时管路试件所在环境为标准大气压下，压力为101 325 Pa(默认管内压力为标准大气压)。开启振动控制仪，对试件进行扫频试验，用东华信号采集仪采集管路试件沿Z轴方向的加速度值，并将时域信号转换为频域信号，提取出管路试件的固有频率并记录，这里的频率取到2 000 Hz 即可。

6) 按照上述步骤对试件再进行5次扫频振动试验，记录试验数据，试验过程如图2所示。

表2是根据6次试验数据提取出的压接修理民机液压直管的前6阶固有频率值。由第1次试验结果数据得出的频率-加速度曲线见图3。

图2 振动试验过程Fig.2 Process of vibration test

表2 压接修理直管的前6阶固有频率

Table 2 First 6 natural frequencies of straight pipes repaired by pressing Hz

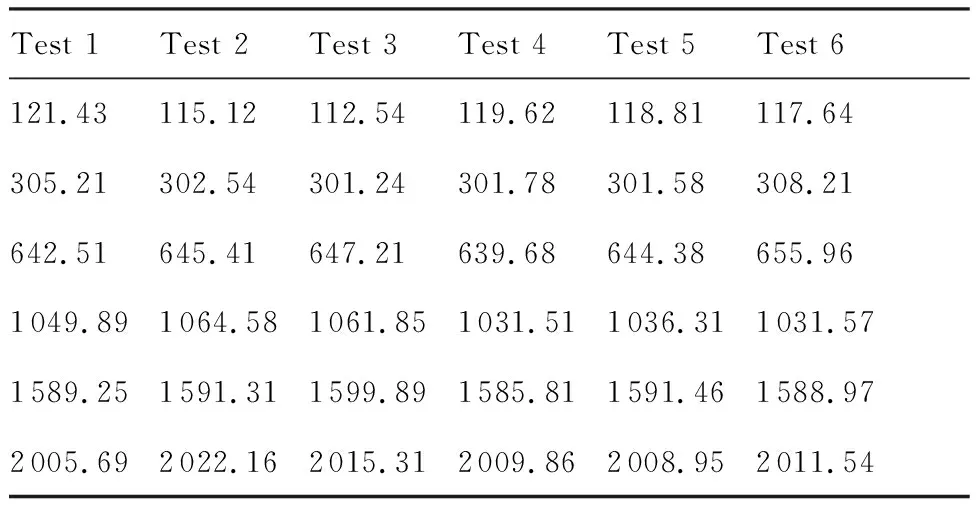
Test 1Test 2Test 3Test 4Test 5Test 6121.43115.12112.54119.62118.81117.64305.21302.54301.24301.78301.58308.21642.51645.41647.21639.68644.38655.961049.891064.581061.851031.511036.311031.571589.251591.311599.891585.811591.461588.972005.692022.162015.312009.862008.952011.54

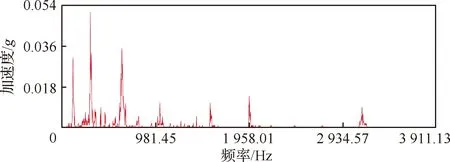
图3 管路的频率-加速度曲线Fig.3 Variation of acceleration with frequency of pipeline

2 压接修理民机液压直管仿真分析

在ANSYS Workbench中建立管路的有限元模型，在进行有限元分析时各参数见表3，这里忽略管路本身的质量。

表3 管路特性参数Table 3 Characteristic parameters of pipelines

2.1 压接修理液压直管有限元建模

ANSYS Workbench中的模块连接如图4所示。在距入口300 mm处截断，用长为38.86 mm、压制区域公差为4 mm的压接管进行压接。在模型中，根据不同接触类型的特点，将管路和压接接头的接触区域定义为绑定接触。由于管路通过夹具固定在试验台上，这里默认管路两端固支，悬空放置，在管路两端施加固定约束即可。压制区域用德驰公司的压接钳，施加10 000 PSI(70 MPa)(1 PSI=0.007 MPa)压力[18]，具体见图5。

管路整体采用扫略法进行划分，管路和压接接头的接触区域属于应力集中产生的地方，需要进一步细化，对流体进行网格划分时不用考虑接触部分，但是要考虑边界层的影响，这里在流固交界面插入边界层，设置边界层的层数为5层，第一层厚度设为0.1 mm，见图6。

模拟民机液压系统在标准大气压下的振动环境，在FLUENT模块中设置入口、出口以及交界面耦合情况等，并在FLUENT-solve中设置解算方法，最后点击calculation解算。其中添加流体流速为1 m/s，管内压力为101 325 Pa。将FLUENT计算结果导入Workbench中,得如图7所示载荷图。

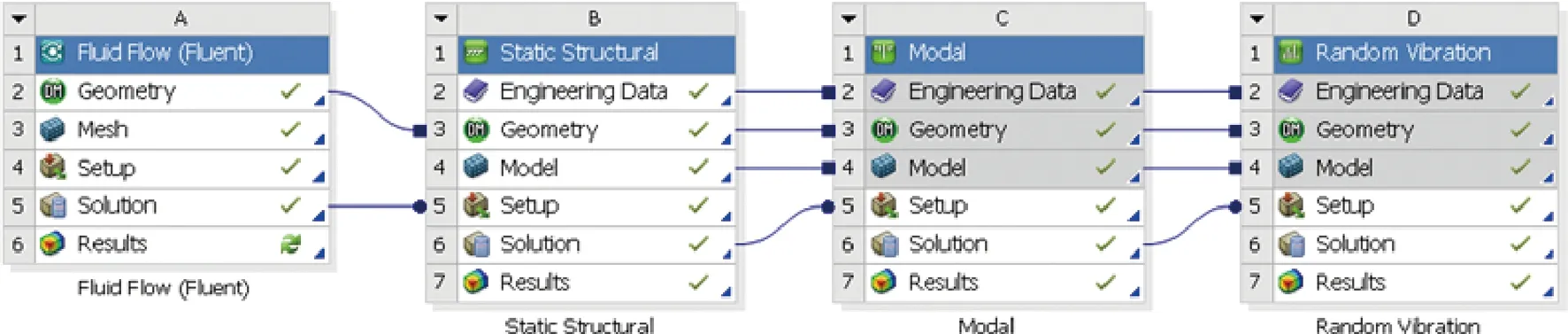
图4 Workbench和FLUENT的流固耦合分析模块Fig.4 Fluid-structure coupling analysis module of Workbench and FLUENT

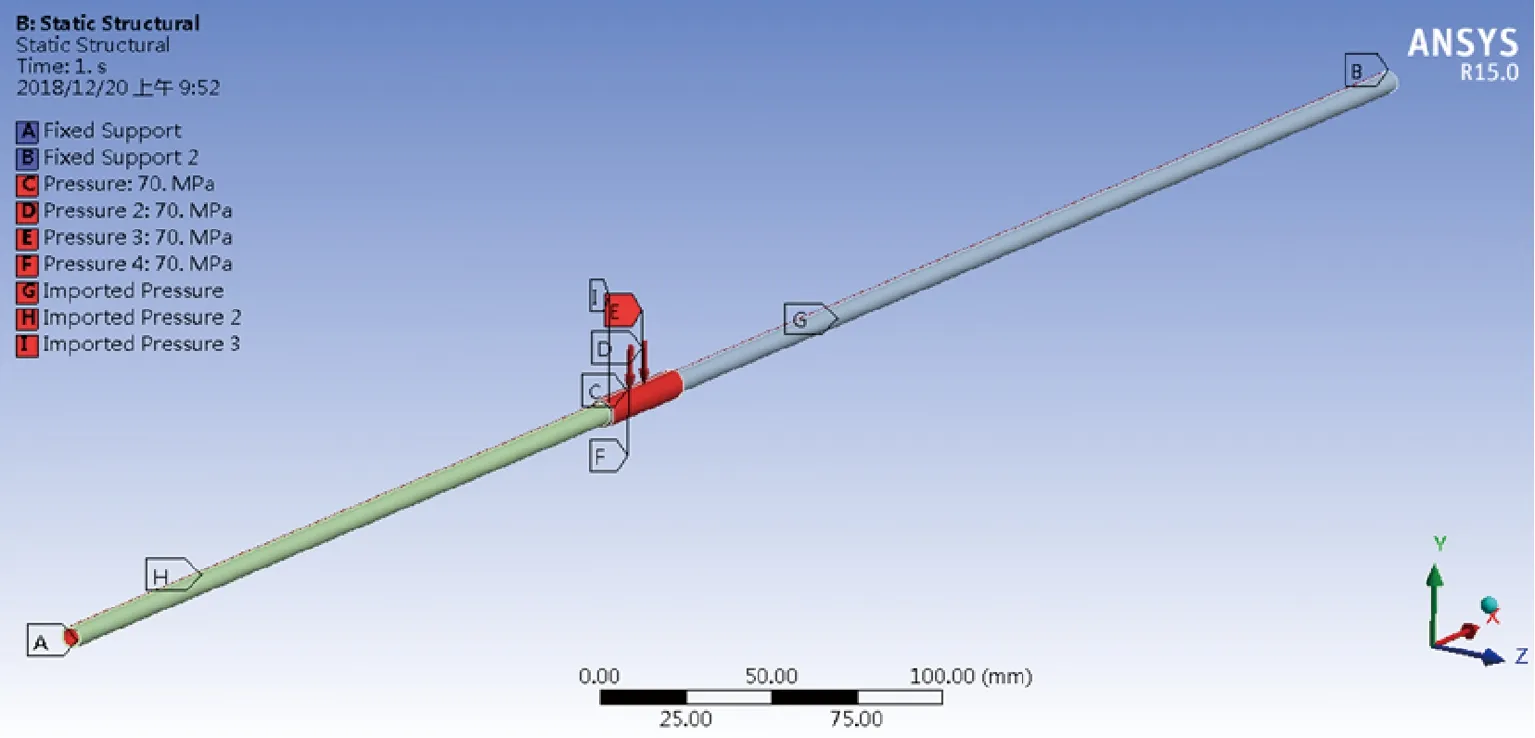
图5 压接修理导管模型Fig.5 Model of pipe for crimping repair

图6 流体网格划分Fig.6 Fluid meshing

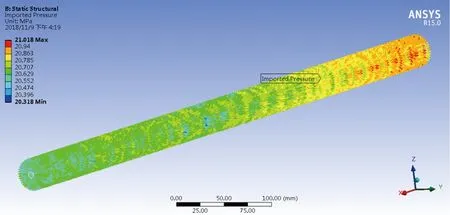
图7 流体载荷Fig.7 Fluid load

2.2 压接修理液压直管有限元仿真

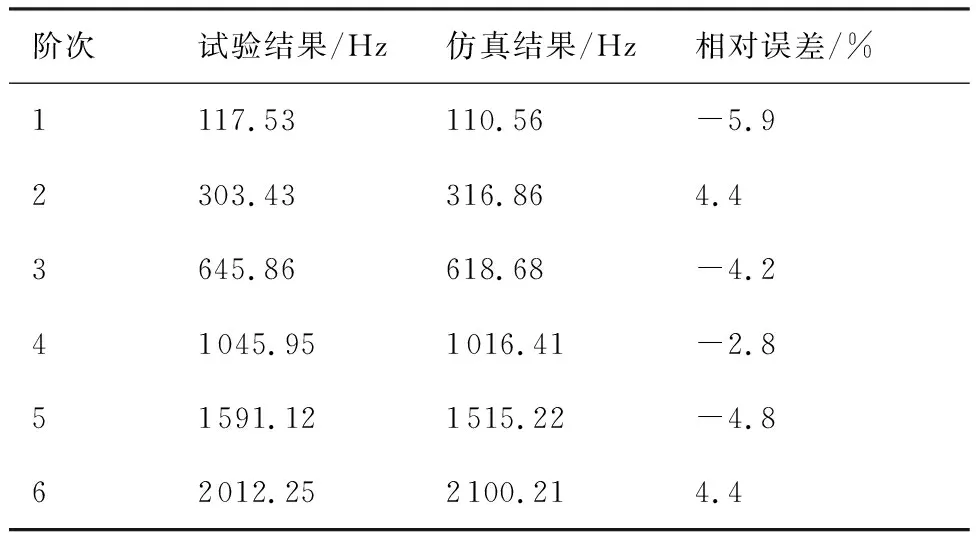
对压接修理民机液压直管进行振动特性分析，得到前6阶固有频率，表4为压接修理民机液压直管前6阶固有频率试验结果平均值与仿真结果及其相对误差，其结果拟合曲线见图8。

由表4和图8知，试验结果平均值与仿真结果的误差均在5%左右，且二者曲线基本拟合，证明了在ANSYS Workbench中对振动环境下的压接修理民机液压直管进行有限元仿真的合理性。

表4 压接修理直管固有频率对比

Table 4 Comparison of natural frequencies of straight pipes for crimping repair

阶次试验结果/Hz仿真结果/Hz相对误差/%1117.53110.56-5.92303.43316.864.43645.86618.68-4.241045.951016.41-2.851591.121515.22-4.862012.252100.214.4

图8 试验与仿真结果拟合曲线Fig.8 Fitting curves of test and simulation results

3 压接修理民机液压直管的固有频率、应力及位移响应分析

3.1 压接修理民机液压管路受力分析

1) 管路整体受力分析

本文研究的管路属于薄壁管，当管路受液体压力与温度共同作用时，其环向应力为

(1)

式中：p为流体压力,MPa；D为管路外径,mm；δ为管路壁厚,mm。

纵向应力为

σz=μσt±αEΔt

(2)

式中：μ为管道的泊松比，取0.31；αE为管道的线胀系数,K-1；Δt为管道在飞机运行和停放时的温度差,℃。

由于管道产生纵向拉应力，则σz<σt。

2) 压接接头受力分析

管路压制区域相当于双层薄壁组合管，压接管与管路间的接触面产生的接触压力为q，同时承受内部流体压力p，管路压制区域剖面如图9所示。

在q和p共同作用下，压制区域产生的环向应力分别为σtq和σtp，具体为[19]

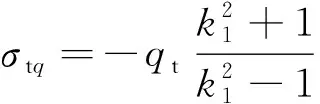
(3)

式中：qt为环向接触压力, MPa；k1=r/r1。

(4)

式中：k2=r2/r;k=r2/r1。

压制区域纵向应力σzq和σzp分别表示为

σzq=-qπdLf/A

(5)

式中：A为压接管接触面的截面面积;q为压接管与管路间的接触面产生的平均接触压力；d为管路内径；L为压制区域的长度；f为压接管与管路接触面间的摩擦系数。

接头接触面在内压p作用下的纵向应力可表示为

(6)

图9 压制区域简化剖面Fig.9 Simplified section of suppressed area

由上述分析可知：为使压接接头保持与管路等强度，需使接头接触面产生足够大的接触压力，因此|σtq||σt|, |σtq||σtp|，即压接接触面承受接触压力作用下的环向应力远大于管路的环向应力和压接接触面承受内压力作用下的环向应力；同理|σzq||σzp|, |σzq||σt|，因此|σzq||σz|。

综上，压接修理管路产生最大应力的位置为压接接头处，因此，管路的最大变形也发生在压接接头处。

3.2 压制区域公差-频率、应力及位移分析

以压制区域公差为变量，分别建立压制区域公差为0 mm、1 mm、2 mm、3 mm、4 mm、5 mm、6 mm 以及7 mm时压接修理液压直管有限元模型，其中压接长度为38 mm，直管长度为700 mm。由于需模拟飞机正常运行时的工作状态，因此在FLUENT模块中设置流体流速为4 m/s，管内压力为21 MPa[20]。直管两端施加固定约束，压制区域施加70 MPa的压力，对直管施加沿Z轴方向的随机振动载荷。图10为1阶固有频率随压制区域公差变化曲线。

由图10知，压制区域公差为0 mm、3 mm和4 mm时，前6阶固有频率较高，且1阶固有频率高于2 000 Hz。

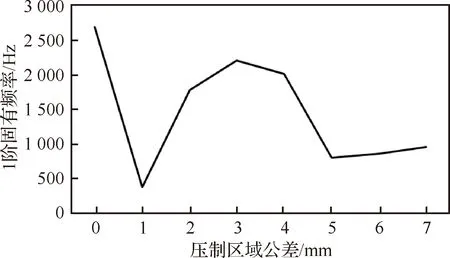
图10 1阶固有频率随压制区域公差变化曲线Fig.10 Variation curve of first-order natural frequency with tolerance of pressure zone

最大应力、沿Y、Z轴方向的最大位移随压制区域公差变化曲线见图11和图12。

由图11和图12知，压制区域公差为0 mm、4 mm 和6 mm及以上时，沿Y、Z轴方向的最大位移均较小，最大应力在压制区域公差为4 mm和6 mm时较小。

综上，压制区域公差为4 mm时管路的1阶固有频率达2 016.8 Hz，最大应力为1.11×108MPa，最大位移响应分别为59.961 mm、111.13 mm，此时压接修理效果较好。

图11 最大应力随压制区域公差变化曲线Fig.11 Variation curve of maximum stress with tolerance of pressure zone

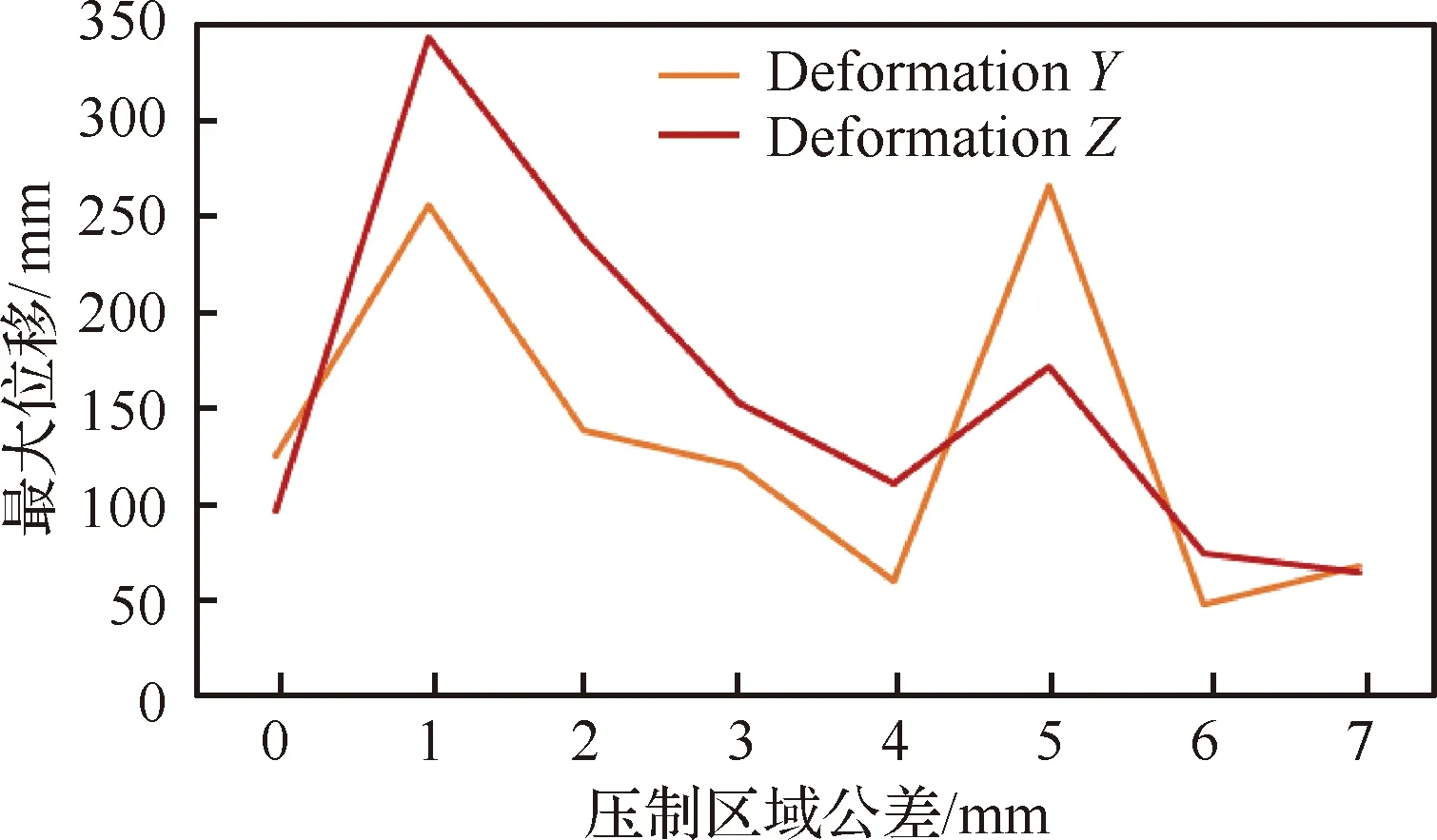
图12 最大位移随压制区域公差变化曲线Fig.12 Variation curves of maximum displacement with tolerance of pressure zone

3.3 压接长度-频率、应力及位移分析

以压接长度为变量，分别建立压接长度为38.44 mm、38.58 mm、38.72 mm、38.86 mm、39.00 mm、39.14 mm、39.28 mm以及39.42 mm时压接修理民机液压直管有限元模型，其中压制区域公差为4 mm，直管长度为700 mm。其他条件与3.2节一致。得以上8组模型前6阶固有频率，图13为1阶固有频率随压接长度变化曲线。

由图13知，压接长度为38.44 mm、39.00 mm和39.14 mm时，1阶固有频率均高于1 000 Hz。

最大应力、沿Y、Z轴方向的最大位移随压制区域公差变化曲线见图14和图15。

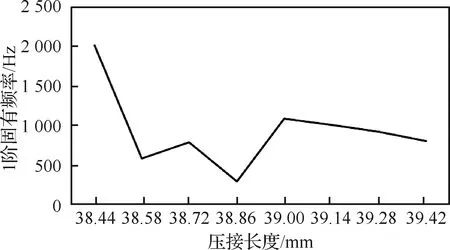
图13 1阶固有频率随压接长度变化曲线Fig.13 Variation curve of first-order natural frequency with crimping length

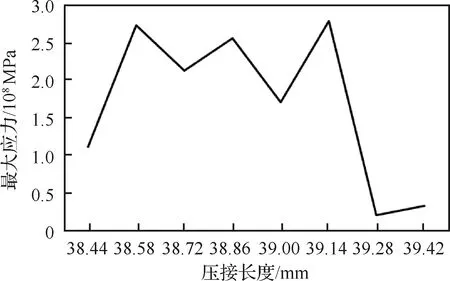
图14 最大应力随压接长度的变化曲线Fig.14 Variation curve of maximum stress with crimping length

图15 最大位移随压接长度的变化曲线Fig.15 Variation curves of maximum displacement with crimping length

由图14和图15知，压接长度为38.72 mm、39.28 mm及以上时，沿Y、Z轴方向的最大位移较小；压接长度为39.00 mm时，最大应力、沿Y、Z轴方向的最大位移也较小，压接长度为38.44 mm和39.28 mm及以上时，最大应力较小。

综上，在压制区域公差为4 mm的情况下，直管的压接长度为39.00 mm时，其1阶固有频率达1 089.8Hz，最大应力为1.71×108MPa，最大位移响应分别为77.985 mm、110 mm，压接修理效果较好。

3.4 典型压接修理民机液压管路振动响应分析

对3.2节和3.3节中的16组模型分别进行振动响应分析，得到最大应力以及沿Y、Z轴方向的最大位移响应的位置分别见表5和表6。

分别取压制区域公差为4 mm，压接长度为38 mm和39 mm的压接修理民机液压直管，进行振动响应分析，其最大应力以及沿Y、Z轴方向的最大位移响应云图见图16和图17。

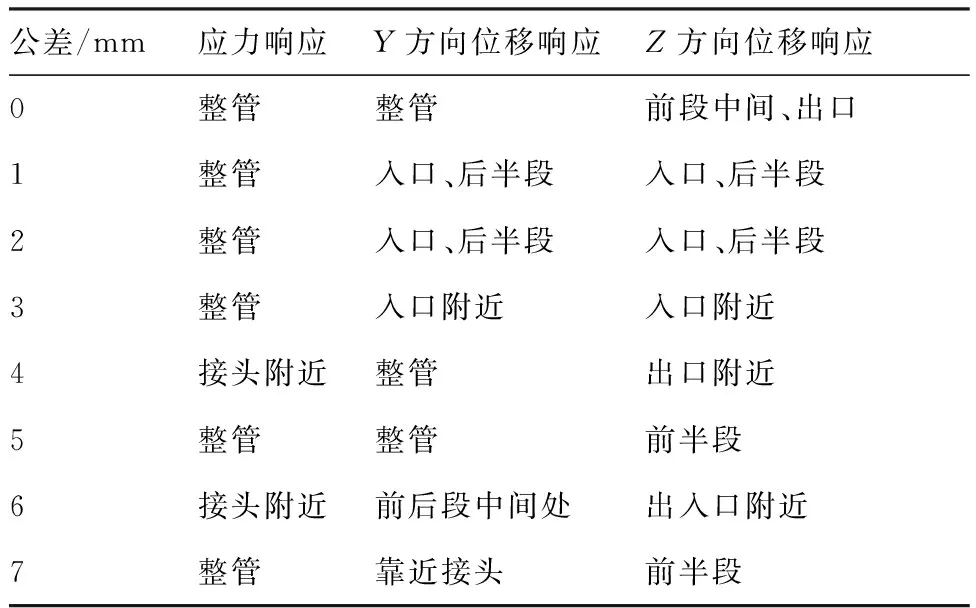
表5 以压制区域公差为变量的管路响应位置

表6 以压接长度为变量的管路响应位置

图16 压接长度为38 mm时的振动响应Fig.16 Vibration response of 38 mm crimping length

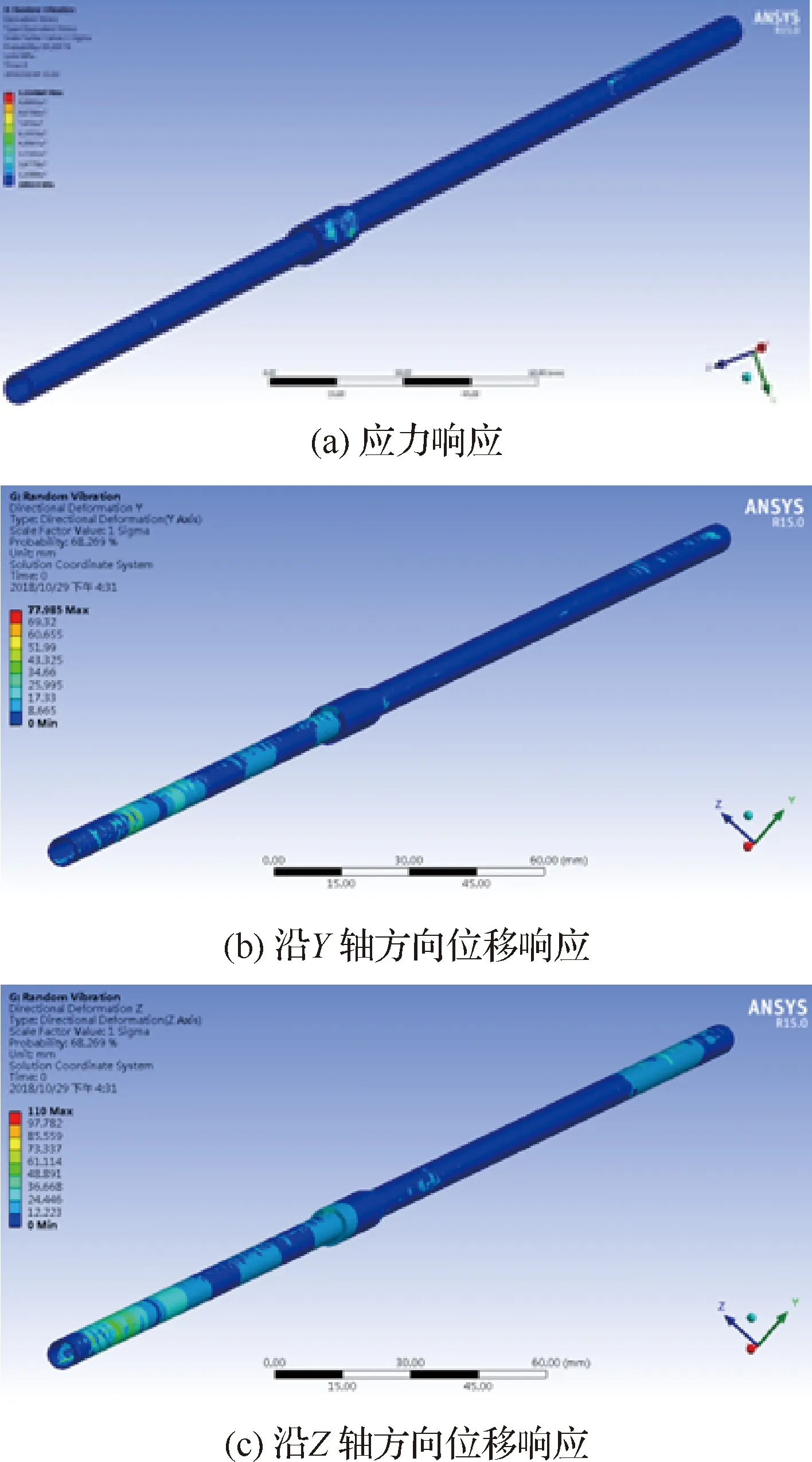
图17 压接长度为39 mm时的振动响应Fig.17 Vibration response of 39 mm crimping length

由表5和表6以及图16和图17可知，压接长度为38 mm，压制区域公差为4 mm时，最大应力出现在压接接头处，但最大变形却不是出现在接头处，与受力分析结果不符；而压制区域公差为4 mm，压接长度为39 mm时，最大应力以及最大位移均出现在压接接头处，符合受力分析结果。

4 结 论

1) 对比压接修理民机液压直管的仿真结果与试验结果平均值可知，误差均在5%左右且曲线拟合良好，验证了运用ANSYS Workbench对振动环境下的压接修理民机液压直管进行有限元建模和仿真分析的合理性。

2) 对压接修理民机液压直管进行受力分析可知，压接接头处出现最大应力与变形；以压制区域公差和压接长度为变量进行压接修理民机液压直管的振动特性分析结果显示：压接长度为39 mm，压制区域公差为4 mm时，管路的固有频率较高，应力及位移响应也较小，压接修理效果最佳，且该压接修理尺寸下的最大应力与最大位移响应均发生在压接接头区域，与受力分析结果相符。