格点量子色动力学组态产生和胶球测量的大规模并行及性能优化①

田英齐,毕玉江,贺雨晴,马运恒2,,刘朝峰2,,徐 顺

1(中国科学院 计算机网络信息中心,北京 100190)

2(中国科学院大学,北京 100049)

3(中国科学院 高能物理研究所,北京 100049)

格点量子色动力学(Lattice Quantum Chromo Dynamics,LQCD) 是描述夸克和胶子之间的强相互作用的理论,它将连续时空离散成有限大小的四维超立方晶格,将QCD 理论中的夸克场放在超立方晶格的格点上,晶格点之间的连线上放置胶子场.可测量的物理量是这两种场的函数,夸克场和胶子场的分布情况反映了QCD 的动力学性质,所以只要在格子上给定了这两种场的分布,原则上就能计算所有物理量(的期望值),因此格点QCD 模拟[1]是一个重要的基础方法,具体来说是目前已知能系统研究夸克及胶子间低能强相互作用的不可缺少的非微扰计算方法.

格点QCD 的一个重要研究课题是胶球性质的研究.胶球是传统夸克模型中没有的强子态,由能发生自相互作用的胶子组成.我国的BESIII 合作组一直在寻找胶球,并发现了一些可能的候选者.但要确认它们,需要将理论计算与实验测量结合起来,因此胶球性质的理论研究是一个重要的前沿课题,胶球的理论计算工作有助于基础物理科学的新发现.

格点QCD 是一个典型的计算密集型同时也是通信密集型的计算工作.常用马可夫链实现蒙特卡洛重点抽样,并且采用各种高级算法如pseudo-heat-bath 算法来加速组态生成过程的收敛；高精度大规模组态抽样的文件输出需要高效的计算IO；格点化的场近程作用是四维stencil 计算的一种具体形式,其计算效率不仅受处理器频率影响也受内存缓存大小影响；另外格距越小,计算物理观测结果越精确,但带来的计算量指数增加,造成了很多物理研究中采用近似算法.总之,格点QCD 对并行计算优化提出了很高的需求.

针对格点QCD 的并行计算优化受到高度重视,超级计算机上格点QCD 计算优化及作业调度优化多次获得戈登贝尔(Gordon Bell) 奖(分别是1987年、1995年、1998年和2006年,以及2018年入围决赛).2005年前后,IBM、RBC/UKQCD和RIKEN 等设计了专门用于格点QCD 计算的超级计算机QCDOC(QCD on Chips),取代了其更早的QCDSP (QCD on DSPs)机器,IBM 后来还打造了更强大的Blue Gene/L平台,其Pavlos Vranas 团队基于该平台实现了3.2 万核12 Tflops 的格点QCD 应用高性能计算,从而获得了2006年的戈登贝尔奖；2018年Pavlos Vranas 再次采用GPU 加速格点QCD 计算,在美国Sierra和Summit超算平台上以高效的计算性能晋级了当年的戈登贝尔决赛[2].格点QCD 已逐渐成为美国、日本及欧洲超算平台上的重要应用[3].

当前以美国USQCD 组织研发的格点QCD 软件套件为领域内主流软件工具,其为四层软件框架,最上层应用层包括Chroma、CPS和MILC 等,下面三层为支撑库层,分别实现消息通讯、数据结构定义和基本算法实现.MILC 软件工具也成为SPEC CPU2006 基准测试程序[4].QUDA 是基于CUDA 的格点QCD 计算库[5],实现了较底层的计算加速,可以和上层的Chroma和MILC 等集成.Mikhail Smelyanskiy 等人基于多核处理器的Cache 架构进行了格点QCD 的线程化MPI 优化,相关工作发表在2012年Supercomputing Conference会议上[6],Issaku Kanamori 基于Intel KNL和Oakforest-PACS 超算系统做了格点QCD 设计实现的讨论,涉及SIMD和MPI 优化方面[7].日本高能加速器研究机构(KEK) 也于2009年开始了用于格点QCD模拟的Bridge ++软件工具研发[8].我国存在一个“中国格点QCD”的合作组,当前正在努力推出国际上较有影响的格点QCD 计算软件.

本文研究工作探讨格点QCD 计算的瓶颈问题,并提出有效的并行优化计算方案.相关程序原始代码由中科院高能物理研究所研究员、“中国格点QCD”成员陈莹提供.为了实现其大规模并行计算、本文进行多方面的并行计算分析和性能优化研究.

1 格点QCD 模拟的基本流程

本节给出在淬火近似下格点QCD 生成规范场组态的基本流程.一个具体的胶子场分布叫做一个组态,产生上述的组态需要涉及名为马可夫链的随机行走过程.整个链条通常从一个最简单的或随机的胶子场分布开始起步.每一次步进更新就意味着由当前的场分布更新到另一种物理上允许的分布.

组态生成与测量流程可以分为如下几步：

1) 从一个给定的场分布开始,计算每个link 的周遭环境,使用pseudo-heat-bath 算法计算link 更新的几率,据此决定是否将其更新,对更新造成的link 形变加以修正；

2) 重复以上过程将整个格子上的所有link 更新若干次,直到达到热平衡,热平衡之后继续不断更新格子上的link,使之成为新的组态,将新的组态导出保存；

3) 在生成好的组态上测量胶球关联函数,继续生成组态,保存和测量,直到测量了足够多的组态样本.

更详细的程序流程见图1.

图1 胶子场组态生成与测量的流程图

在我们的程序中使用的pseudo-heat-bath 算法用于加快收敛.当我们利用马可夫链抽样,每个样本点对应的胶子场分布都是我们所要的组态.在有夸克场时,胶球与通常介子态之间的混合会给研究增加复杂度,需要更大的计算量.因此作为第一步,忽略夸克场的所谓淬火近似下的模拟计算具有重要意义.对淬火组态产生程序的优化,目的在于给出更多的组态,从而得到更大的统计量和更好的信号.淬火近似下胶球谱的研究工作和J/psi 粒子辐射衰变到标量胶球或张量胶球的淬火近似研究工作[9-11],其结果都发表在物理学一流学术期刊上.这些计算中用到组态产生程序正是本研究优化的对象.

程序实现中主要涉及的功能模块有：

1) 数据初始化模块：体系的格点划分,内存数组分配等；

2) 组态生成模块：利用pseudo-heat-bath 算法生成满足分布的组态；

3) 组态计算模块：基于抽样的组态计算胶球的物理性质；

4) 辅助分析模块：组态验证、统计计时、并行写组态等.

2 并行计算关键问题

QCD 理论是一个基于SU(3)规范对称性的理论.在格子上,每一条晶格连线上的胶子场的值由一个3 乘3 的SU(3)复矩阵描写：Uμ(x).组态生成程序从一个给定的场分布开始,计算每条连线(也叫link 变量)的周遭环境,这里涉及大量矩阵计算,并且每个格点需要做独立性分析以适合并行化计算处理.

我们的程序按照pseudo-heat-bath 算法来更新格子上的每个link 变量的值,按以下几率分布将一个link 变量的值从Uμ(x)更新为Uμ(x)’：

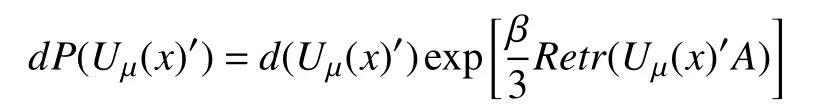
其中,A刻画该link 周围的环境,由其他link 变量对应的矩阵值的乘积给出.计算A的过程中会涉及到相应link (link 构成订书针的形状,被称为“staple”)相乘的计算,其示意图如图2.

图2 link 周围环境(staple)计算示意图

要计算图中的link 变量对应的A,需要对其近邻以及次近邻的格点上相关的link 变量的乘积(即3×3 复矩阵的矩阵乘积)进行求和,即对上图中的8 个“staple”进行求和：

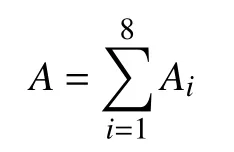
其中,Ai为每个staple 内涉及的link 的乘积,以图2中的Ⅰ为例,其计算公式如下：

由此可以看出,这里涉及大量3×3 复矩阵的矩阵乘积计算优化问题.

由于要更新一个link 变量,只与其近邻和次近邻的相关link 有关,而与其他link 无关.因此这些相互无关的link 之间可以并行处理.传统的格点QCD 程序一般采用blocking和even-odd 算法进行并行.该算法将相应的link 分配到不同的block 上,根据block 的x、y、z、t的坐标之和的奇偶分为两组,每组内可以进行并行计算.然而我们的胶球模拟中涉及到了近邻以及次近邻的相互作用,因此需要首先将24 个block 组合为一个hyper-block,之后对hyper-block 进行evenodd 的并行计算,来生成相应的组态.一个二维结构格子的Hyper-blocking 与even-odd 算法示意如图3.

图3 even-odd 算法示意如图

图3中同色的虚线框之间可以进行并行计算.

另外格点QCD 需要重复以上将整个格子上的所有link 的值更新若干次,达到热平衡,热平衡之后继续不断更新格子上的link 的值,使之成为新的组态,而组态的存储空间占用也比较大,因此将新的组态导出保存也是并行化时需要考虑的问题.

3 并行分析与优化策略

3.1 瓶颈与热点分析

为了实现进行大规模的格点QCD 计算,我们首先需要分析程序运行可能的热点.原型程序采用消息传递接口(Message Passing Interface,MPI)来实现多节点并行处理,采用基于格点区域计算任务划分的方式来实现并行处理,需要在各个MPI 进程之间进行格点边界通信.通信占比与格子的划分方式有关,具体地说与子格子的面积体积比有关.更小的面积体积比有更小的通信占比.我们知道同样体积的情况下,正方体比长方体有更小的面积体积比,因此导致了在通常情况下,x、y、z方向的格子规模相同,且划分方式相同,t方向格子规模与划分方式可以与x、y、z方向不同.因而在格子规模V和计算节点规模N确定的情况下,确定划分方式即为求以下方程的正整数解：

其中,lt是t方向的子格子大小,lxyz是x、y、z方向的子格子大小.该方程的正整数解一般是确定的,因而不能灵活的协调通信与计算的比例,来获取更优的性能.为了更加灵活的分配计算任务,获取通信与计算的平衡,我们可以加入多线程(如OpenMP)的并行处理,更加充分的利用计算资源.

基于原型程序的初步测试,我们发现在常用的计算规模下,计算耗时占比60%以上.此程序的计算中,涉及大量3×3 复矩阵的矩阵乘积计算,是此程序的计算热点.

另外,运行时输出组态文件无疑也是一个性能瓶颈,尤其是在格子规模较大的情况下.对于964 大小的格子,组态文件大小为40 GB 以上.然而原型程序采用了串行输出组态文件的方法,耗时极大,因此也需要采取优化措施.

因此通过分析与测试,为了实现程序有效并行处理,我们考虑以下方面：

1)平衡通信与计算占比

2)复矩阵矩阵乘等数值计算函数

3)输出组态文件

以下分别介绍这几方面的计算瓶颈或计算热点的优化设计.

3.2 MPI+OpenMP 并行优化

针对胶球模拟的特点,在xyzt四个维度上均可以进行并行.程序可以设置各个方向分别的划分方式.假设格子的体积设置为(Nt,Nx,Ny,Nz),在t、x、y、z方向分别划分为mt、mx、my、mz份,则每个MPI 进程上的格子体积为(Nt/mt,Nx/mx,Ny/my,Nz/mz),划分方式记为(mt,mx,my,mz).以(2,2,2,2)划分方式为例,4 个维度的并行分割方式如图4所示.

图4 MPI 并行划分方式(2,2,2,2)示意

基于前述的分析,对于相同规模的格子,使用MPI+OpenMP 的并行方式,可以有效增加单个MPI 进程上格子的规模,从而降低子格子的面积体积比,从而减少通信的占比.因此我们采用了动态负载平衡的方法,在MPI 进程内部进行OpenMP 的并行.图5以二维结构示意单个MPI 进程内部2 个OpenMP 线程情况下的OpenMP 并行情况：

图5 OpenMP 并行示意图

3.3 矩阵操作的向量化优化

在程序中,涉及到的计算主要是3×3 的复矩阵的矩阵乘计算,即两个3×3 的复矩阵相乘,以及复矩阵与矩阵的厄密共轭矩阵相乘.具体计算如下所示：

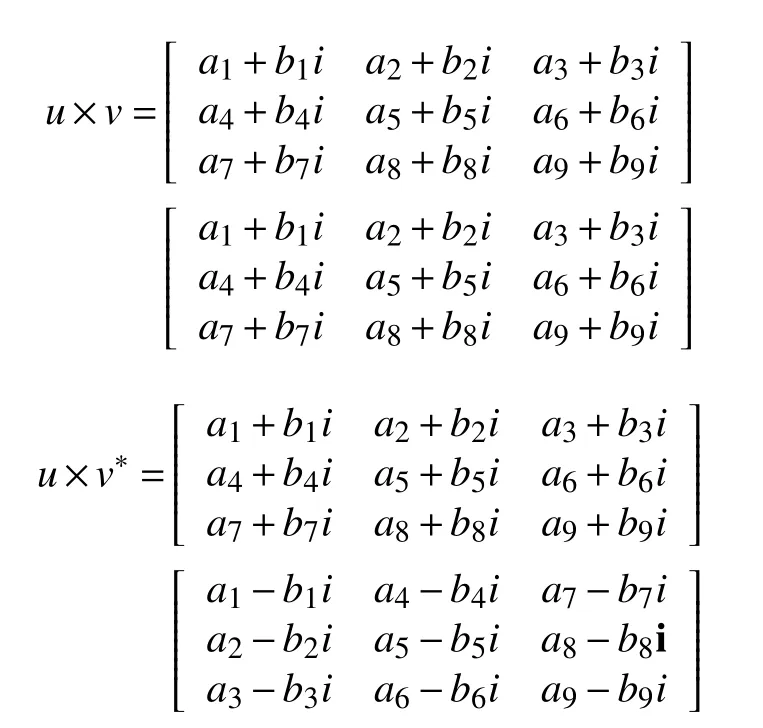
我们针对复矩阵矩阵乘操作,设计了多种不同的计算方法,以下将分别介绍：

1) 我们基于结构体的数组转化为数组的结构体(AoS to SoA)的思想,设计了数组长度可变的结构体数组,用来存储中间数据,提高了计算效率.经过测试,结构体内数组长度为8 时的效果最好.

2)我们将复矩阵矩阵乘的数学算式完全展开,利用编译器的自动向量化功能进行相关代码的向量化.

3) 我们针对AVX-512 指令集架构,利用Intel Intrinsics 设计了手动向量化的算法.对于这样的矩阵计算,我们可以将v矩阵的行向量实部和虚部[c1,d1,c2,d2,c3,d3]组装为一个向量,针对实部和虚部采用_mm512_fmaddsub_pd()函数进行计算.

3.4 输出组态文件的优化

原始的组态文件按照一般多维数组的存储方式,以行主元的方式进行存储,即依次按照z、y、x、t下标由小到大进行存储.原程序依据该存储方法由0 号进程进行数据收集及输出到文件的工作.以42大小的格子,(2,2)划分方式为例,4 个MPI 进程的组态文件输出方式如图6所示.

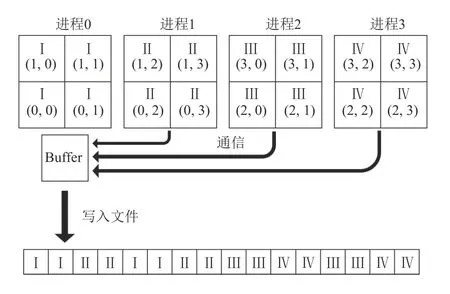
图6 MPI 并行写入优化前算法示意图

对于N个进程的情况,原始的输出方式需要进行的通讯量为(N-1)×Vsub,其中Vsub为子格子的大小.而且需要进行N×mt×mx×my次不连续的写操作.

我们修改了组态文件的数据排布方式,将整个文件划分为N 部分,并在每个部分内按照数据连续的方式进行排布,依次实现了多个MPI 进程并行输出组态文件的算法.采用此种方法后,理论上没有通信操作,也没有不连续的内存写操作,可以极大的提高输出组态文件的性能.并行写采用了MPI-IO,MPI 中可以使用 mpi_file_open 让所有进程都打开同一个文件,使用mpi_file_write_at 函数独立互不干扰地写每个进程自己负责的数据.图7展示了优化后的数据写入方式：

图7 MPI 并行写入优化后算法示意图

4 实验结果与分析

4.1 实验准备

我们在“天河2 号”超级计算平台以及KNL 平台上测试了我们的代码,测试平台的信息如表1所示.

表1 软硬件环境清单

其中“天河2 号”超级计算机不支持AVX 指令向量化,而Intel KNL 支持AVX512 指令向量化.

4.2 OpenMP 多线程加速测试

基于前述3.1 节的整体分析与3.2 节提出的OpenMP多线程加速方案,我们设定了两种格子规模和计算规模的情况,考察MPI 单节点上采用OpenMP 多线程调整计算与通信占比以优化并行效率的效果.同时我们也考察了优化前后程序强可扩展性和弱可扩展性的对比情况.

4.2.1 常规规模测试结果

我们首先针对常用的格子与计算规模,进行了程序优化的测试.我们设定格子大小为96×483,使用了5184 个计算核心,测试结果如表2.

表2 常规规模测试结果

从测试结果可以看出,在规模不变的情况下,原始的MPI 并行并不是最优结果.随着OpenMP 线程数的增加,性能逐渐提高,达到了理想的计算效率.较小规模的情况下最高达到了3.32 倍的加速.

4.2.2 大规模测试结果

我们又选择了当前环境下可使用的最大计算规模进行了测试.我们设定的格子大小为964,使用了41 472个计算核心,测试结果如表3.

表3 大规模测试结果

从测试结果可以看出,在规模不变的情况下,原始的MPI 并行同样不是最优结果.加入OpenMP 并行后,可以使得格子的划分更加灵活,可以找到合理的划分方式,达到理想的计算效率.较大规模的情况下最高达到了1.37 倍的加速.

4.2.3 划分方式对计算效率的影响分析

根据前述3.1 与3.2 节的分析,我们可以知道减少通信占比的方法是增大子格子的面积体积比.在常规规模的测试中,我们可以看出,通过加入OpenMP 并行,可以有效减小子格子的面积体积比,取得了很好的加速效果.对于大规模的测试结果,我们发现单纯增大子格子面积体积比并没有导致计算性能的持续提高,针对这一情况,我们分析原因与计算机的网络结构有关.计算任务在节点上的分配方式需要进一步的优化研究.

4.2.4 强可扩展性测试

针对MPI+OpenMP 并行方案,我们测试了程序的强扩展性.我们对比了只有MPI 并行的情况和MPI 与OpenMP 混合并行的情况.强扩展性测试用例的格子大小为644,最高并行达到了4096 核.测试结果如图8所示.

图8 强扩展性测试结果

结果显示在应用了OpenMP 多线程加速后,强扩展性有了明显的提高.

4.2.5 弱可扩展性测试

我们针对MPI+OpenMP 并行方案,测试了程序的弱扩展性.弱可扩展性测试的规模为：每个核上分配有84大小的格子,依次测试了256 核～6144 核的计算结果.测试结果如图9.

图9显示了各次计算中单步生成组态的计算时间,在理想情况下,单步时间应该是保持不变的,然而随着体系的增大,实际会有所增加.我们用最小二乘法线性拟合数据结果,得到了两条拟合曲线的斜率,以此来评价程序的弱扩展性.结果显示在应用了OpenMP 多线程加速后,程序的弱可扩展性也得到了提高.

图9 弱扩展性测试结果

4.3 向量化优化测试

针对3.3 节提出的向量化优化方案,我们在KNL平台上测试了AVX-512 向量化优化的计算结果.我们通过-xMIC_AVX512 编译选项控制向量化开关,进行了向量化与不向量化的测试.测试中使用了324大小的格子,运行在MPI+OpenMP 的模式下,MPI 绑定CPU采用I_MPI_PIN_DOMAIN=omp：compact,OpenMP设置亲缘性KMP_AFFINITY=compact.测试基准为未向量化的Fortran 内置的matmul 函数.后续测试了采用-xMIC_AVX512 编译选项进行向量化的matmul函数；采用AoS to SoA 优化与-xMIC_AVX512 编译选项结合的算法；采用公式展开和编译选项结合的算法；以及采用了Intel Intrinsics 手动向量化的算法.几种算法在16MPI + 1OpenMP 的情况下结果如图10.

图10 16MPI + 1OpenMP 各向量化优化测试结果及加速比

运行在16MPI+16OpenMP 的情况下,测试结果如图11.

图11 16MPI + 16OpenMP 各向量化优化测试结果及加速比

结果显示,几种向量化算法均优于Fortran 内置的matmul 函数的效果,而且都取得了3 倍左右的加速效果.其中基于Intel Intrinsics 的手动向量化算法效果最好,达到了3.17 倍的加速.

4.4 输出组态文件优化测试

针对3.4 节提出的组态输出优化方案,我们测试了未改变数据顺序的MPI 并行输出以及修改数据顺序后的MPI 并行输出算法,以单个MPI 进程输出组态文件的结果为基准,具体实验数据如下：

表4 MPI 并行写组态文件测试结果

表4中“串行写”的数据为测试的基准,并行写”为修改了数据顺序后的并行写算法测试结果,“加速比”为其对应的加速比.通过表4我们可以看出,优化了数据顺序的并行写算法取得了上百倍的加速,最高达到了153 倍.

5 总结与未来工作

格点量子色动力学一直是高性能计算领域的热门应用方向,多年来一直伴随着超级计算机的发展,对高性能计算的发展有强有力的驱动力.本文基于典型的格点QCD 胶球模拟计算程序,采用了多项优化技术,对程序进行了性能分析和并行优化,并实现了大规模的并行测试,并行规模超过4 万核.性能方面,加入OpenMP 多线程并行部分,最高取得了3.32 倍的加速比,在向量化优化矩阵计算部分,最高取得了3.17 倍的加速比,在并行输出组态文件部分取得了153 倍的加速比.

优化后的程序可更有效地产生大量组态,有利于得到更精确的胶球谱.优化后的程序可较容易推广到夸克与胶子组成的混杂态的研究,及普通介子和胶球的混合问题的研究,为高能物理的相关研究提供更加便利的软件工具.

致谢

感谢中国科学院高能物理研究所理论物理室陈莹老师参与讨论和提供帮助,感谢广州“天河2 号”超算工作人员提供的测试支持.